Ratio d'aspect - Aspect ratio
Le rapport hauteur/largeur d'une forme géométrique est le rapport de ses tailles dans différentes dimensions. Par exemple, le rapport hauteur/largeur d'un rectangle est le rapport entre son côté le plus long et son côté le plus court - le rapport largeur/hauteur, lorsque le rectangle est orienté comme un "paysage".
Le rapport hauteur/largeur est le plus souvent exprimé sous la forme de deux nombres entiers séparés par deux points (x:y), moins fréquemment sous la forme d'une fraction simple ou décimale . Les valeurs x et y ne représentent pas les largeurs et les hauteurs réelles, mais plutôt la proportion entre la largeur et la hauteur. A titre d'exemple, 8: 5, 16:10, 1,6: 1, 8 / 5 et 1,6 sont toutes les façons de représenter le même rapport d'aspect.
Dans les objets de plus de deux dimensions, tels que les hyperrectangles , le rapport hauteur/largeur peut toujours être défini comme le rapport du côté le plus long au côté le plus court.
Applications et utilisations
Le terme est le plus souvent utilisé en référence à :
- Graphique / image
- Rapport d'aspect de l'image
- Format d'affichage
- Taille de papier
- Formats d'impression photographique standard
- Formats de films cinématographiques
- Taille d'annonce standard
- Pixel aspect ratio
- Photolithographie : le rapport d'aspect d'une structure gravée ou déposée est le rapport de la hauteur de sa paroi latérale verticale sur sa largeur.
- Les rapports d' aspect élevés HARMST permettent la construction de microstructures hautes sans inclinaison
- Code pneu
- Dimensionnement des pneus
- Dimensionnement de la roue du turbocompresseur
- Rapport d'aspect de l'aile d'un avion ou d'un oiseau
- Astigmatisme d'une lentille optique
- Dimensions de la nanotige
- Facteur de forme (analyse d'image et microscopie)
Rapports d'aspect des formes simples
Rectangles
Pour un rectangle, le rapport hauteur/largeur désigne le rapport entre la largeur et la hauteur du rectangle. Un carré a le plus petit rapport hauteur/largeur possible de 1:1.
Exemples:
- 4:3 = 1. 3 : Certains (pas tous) écrans d'ordinateur du 20e siècle ( VGA , XGA , etc.), télévision à définition standard
- : formats de papier internationaux ( ISO 216 )
- 3:2 = 1.5 : film d'appareil photo 35 mm , l' iPhone (jusqu'à l' iPhone 5 ) s'affiche
- 16:10 = 1,6 : écrans d'ordinateur larges couramment utilisés ( WXGA )
- :1 = 1,618... : nombre d' or , proche de 16:10
- 5:3 = 1. 6 : super 16 mm , un calibre de film standard dans de nombreux pays européens
- 16:9 = 1. 7 : téléviseur grand écran
- 2:1 = 2: dominos
- 64:27 = 2. 370 : ultra-large, 21:9
- 32:9 = 3. 5 : écran super ultra-large
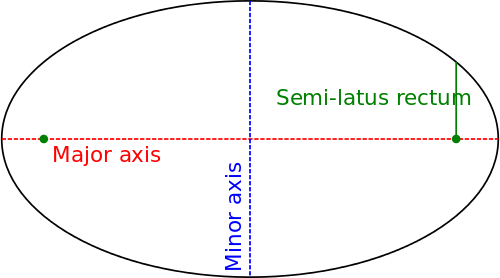
Ellipses
Pour une ellipse, le rapport hauteur/largeur désigne le rapport entre le grand axe et le petit axe . Une ellipse avec un rapport hauteur/largeur de 1:1 est un cercle.
Rapports d'aspect des formes générales
En géométrie , il existe plusieurs définitions alternatives aux rapports d'aspect des ensembles compacts généraux dans un espace de dimension d :
- Le rapport d'aspect diamètre-largeur (DWAR) d'un ensemble compact est le rapport de son diamètre à sa largeur. Un cercle a le DWAR minimal qui est 1. Un carré a un DWAR de .
- Le rapport d'aspect cube-volume (CVAR) d'un ensemble compact est la racine d -ième du rapport du d -volume du plus petit d -cube d'axes englobant parallèle , au d -volume de l'ensemble. Un carré a le CVAR minimal qui est 1. Un cercle a un CVAR de . Un rectangle parallèle à l'axe de largeur W et de hauteur H , où W > H , a un CVAR de .
Si la dimension d est fixe, alors toutes les définitions raisonnables du rapport hauteur/largeur sont équivalentes à des facteurs constants près.
Notations
Les proportions sont exprimées mathématiquement sous la forme x : y (prononcé "x-to-y").
Les rapports d'aspect cinématographiques sont généralement désignés par un multiple décimal (arrondi) de la largeur par rapport à la hauteur de l'unité, tandis que les rapports d'aspect photographiques et vidéographiques sont généralement définis et indiqués par des rapports de nombres entiers largeur/hauteur. Dans les images numériques, il existe une distinction subtile entre le rapport hauteur/largeur d' affichage (l'image telle qu'elle est affichée) et le rapport hauteur/largeur de stockage (le rapport des dimensions en pixels) ; voir Distinctions .
Voir également
- Rapport axial
- Rapport
- Rapports équidimensionnels en 3D
- Liste des formats de films
- Mappage de compression
- Échelle (rapport)
- Orientation verticale
Les références
- ^ Rouse, Margaret (septembre 2005). « Qu'est-ce que le rapport hauteur/largeur ? » . Quel est? . TechTarget . Consulté le 3 février 2013 .
- ^ Rouse, Margaret (septembre 2002). "Large affichage du rapport d'aspect" . afficher . E3 affiche . Récupéré le 18 février 2020 .
- ^ Smith, WD; Wormald, Caroline du Nord (1998). « Théorèmes et applications des séparateurs géométriques ». Actes 39e Symposium annuel sur les fondements de l'informatique (Cat. No.98CB36280) . p. 232. doi : 10.1109/sfcs.1998.743449 . ISBN 0-8186-9172-7.