Automorphisme - Automorphism
En mathématiques , un automorphisme est un isomorphisme d'un objet mathématique à lui-même. C'est, dans un certain sens, une symétrie de l'objet, et une manière de mapper l'objet sur lui-même tout en préservant toute sa structure. L' ensemble de tous les automorphismes d'un objet forme un groupe , appelé groupe d'automorphismes . C'est, grosso modo, le groupe de symétrie de l'objet.
Définition
Dans le contexte de l'algèbre abstraite , un objet mathématique est une structure algébrique telle qu'un groupe , un anneau ou un espace vectoriel . Un automorphisme est simplement un homomorphisme bijectif d'un objet avec lui-même. (La définition d'un morphisme dépend du type de structure algébrique; voir, par exemple, un groupe homomorphism , anneau homomorphism et opérateur linéaire ).
Le morphisme d'identité ( mappage d'identité ) est appelé l' automorphisme trivial dans certains contextes. Respectivement, les autres automorphismes (non identitaires) sont appelés automorphismes non triviaux .
La définition exacte d'un automorphisme dépend du type d'« objet mathématique » en question et de ce qui, précisément, constitue un « isomorphisme » de cet objet. Le cadre le plus général dans lequel ces mots ont un sens est une branche abstraite des mathématiques appelée théorie des catégories . La théorie des catégories traite des objets abstraits et des morphismes entre ces objets.
En théorie des catégories, un automorphisme est un endomorphisme (c'est-à-dire un morphisme d'un objet à lui-même) qui est aussi un isomorphisme (au sens catégorique du terme, c'est-à-dire qu'il existe un endomorphisme inverse droit et gauche).
C'est une définition très abstraite puisque, dans la théorie des catégories, les morphismes ne sont pas nécessairement des fonctions et les objets ne sont pas nécessairement des ensembles. Dans la plupart des contextes concrets, cependant, les objets seront des ensembles avec une structure supplémentaire et les morphismes seront des fonctions préservant cette structure.
Groupe Automorphisme
Si les automorphismes d'un objet X forment un ensemble (au lieu d'une classe propre ), alors ils forment un groupe sous composition de morphismes . Ce groupe est appelé groupe d'automorphisme de X .
- Fermeture
- La composition de deux automorphismes est un autre automorphisme.
- L'associativité
- Cela fait partie de la définition d'une catégorie que la composition des morphismes soit associative.
- Identité
- L'identité est le morphisme d'identité d'un objet à lui-même, qui est un automorphisme.
- Inverses
- Par définition, tout isomorphisme a un inverse qui est aussi un isomorphisme, et puisque l'inverse est aussi un endomorphisme du même objet, c'est un automorphisme.
Le groupe d'automorphismes d'un objet X dans une catégorie C est noté Aut C ( X ), ou simplement Aut( X ) si la catégorie est claire du contexte.
Exemples
- En théorie des ensembles , une permutation arbitraire des éléments d'un ensemble X est un automorphisme. Le groupe d'automorphisme de X est aussi appelé groupe symétrique sur X .
- En arithmétique élémentaire , l'ensemble des entiers , Z , considéré comme un groupe par addition, possède un unique automorphisme non trivial : la négation. Considéré comme un anneau, cependant, il n'a que l'automorphisme trivial. D'une manière générale, la négation est un automorphisme de tout groupe abélien , mais pas d'un anneau ou d'un corps.
- Un automorphisme de groupe est un isomorphisme de groupe d'un groupe à lui-même. De manière informelle, il s'agit d'une permutation des éléments du groupe telle que la structure reste inchangée. Pour tout groupe G il existe un homomorphisme de groupe naturel G → Aut( G ) dont l' image est le groupe Inn( G ) des automorphismes internes et dont le noyau est le centre de G . Ainsi, si G a un centre trivial , il peut être intégré dans son propre groupe d'automorphismes.
- En algèbre linéaire , un endomorphisme d'un espace vectoriel V est un opérateur linéaire V → V . Un automorphisme est un opérateur linéaire inversible sur V . Lorsque l'espace vectoriel est de dimension finie, le groupe d'automorphisme de V est le même que le groupe linéaire général , GL( V ). (La structure algébrique de tous les endomorphismes de V est elle-même une algèbre sur le même corps de base que V , dont les éléments inversibles consistent précisément en GL( V ).)
- Un automorphisme de corps est un homomorphisme d'anneau bijectif d'un corps à lui-même. Dans les cas des nombres rationnels ( Q ) et des nombres réels ( R ) il n'y a pas d'automorphismes de corps non triviaux. Certains sous-corps de R ont des automorphismes de corps non triviaux, qui ne s'étendent cependant pas à tout R (parce qu'ils ne peuvent pas préserver la propriété d'un nombre ayant une racine carrée dans R ). Dans le cas des nombres complexes , C , il existe un unique automorphisme non trivial qui envoie R dans R : conjugaison complexe , mais il existe une infinité ( indénombrable ) d'automorphismes « sauvages » (en supposant l' axiome du choix ). Les automorphismes de champ sont importants pour la théorie des extensions de champ , en particulier les extensions galoisiennes . Dans le cas d'une extension galoisienne L / K le sous - groupe de tous les automorphismes de L fixant K point par point est appelé le groupe galoisien de l'extension.
- Le groupe des automorphismes des quaternions ( H ) en tant que noyau sont les automorphismes intérieurs, par le théorème de Skolem-Noether : Cartes de la forme d' un ↦ bab -1 . Ce groupe est isomorphe à SO(3) , le groupe des rotations dans l'espace à 3 dimensions.
- Le groupe d'automorphisme des octonions ( O ) est l' exceptionnel groupe de Lie G 2 .
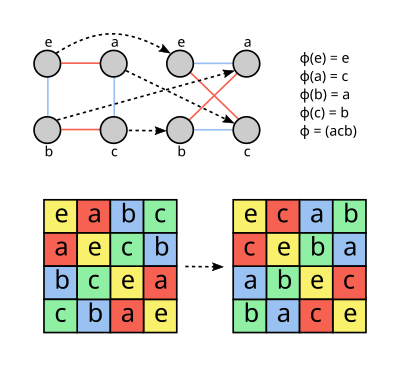
- En théorie des graphes, un automorphisme d'un graphe est une permutation des nœuds qui préserve les arêtes et les non-arêtes. En particulier, si deux nœuds sont joints par une arête, leurs images le sont également sous la permutation.
- En géométrie , un automorphisme peut être appelé un mouvement de l'espace. Une terminologie spécialisée est également utilisée :
- En géométrie métrique, un automorphisme est une auto- isométrie . Le groupe d'automorphisme est également appelé groupe d'isométrie .
- Dans la catégorie des surfaces de Riemann , un automorphisme est une application biholomorphe (également appelée application conforme ), d'une surface à elle-même. Par exemple, les automorphismes de la sphère de Riemann sont des transformations de Möbius .
- Un automorphisme d'une variété dérivable M est un difféomorphisme de M à lui-même. Le groupe d'automorphismes est parfois noté Diff( M ).
- En topologie , les morphismes entre les espaces topologiques sont appelés cartes continues , et un automorphisme d'un espace topologique est un homéomorphisme de l'espace à lui-même, ou auto-homéomorphisme (voir groupe d'homéomorphisme ). Dans cet exemple, il ne suffit pas qu'un morphisme soit bijectif pour être un isomorphisme.
Histoire
L'un des premiers automorphismes de groupe (automorphisme d'un groupe, pas simplement un groupe d'automorphismes de points) a été donné par le mathématicien irlandais William Rowan Hamilton en 1856, dans son calcul icosien , où il a découvert un automorphisme d'ordre deux, en écrivant :
il s'agit donc d'une nouvelle racine cinquième d'unité, liée à l'ancienne racine cinquième par des relations de réciprocité parfaite.
Automorphismes internes et externes
Dans certaines catégories, notamment les groupes , les anneaux et les algèbres de Lie, il est possible de séparer les automorphismes en deux types, appelés automorphismes « intérieurs » et « extérieurs ».
Dans le cas des groupes, les automorphismes internes sont les conjugaisons par les éléments du groupe lui-même. Pour chaque élément a d'un groupe G , la conjugaison par a est l'opération φ a : G → G donnée par φ a ( g ) = aga −1 (ou a −1 ga ; l'usage varie). On peut facilement vérifier que la conjugaison par a est un automorphisme de groupe. Les automorphismes internes forment un sous-groupe normal de Aut( G ), noté Inn( G ); c'est ce qu'on appelle le lemme de Goursat .
Les autres automorphismes sont appelés automorphismes externes . Le groupe quotient Aut( G ) / Inn( G ) est généralement noté Out( G ); les éléments non triviaux sont les cosets qui contiennent les automorphismes externes.
La même définition tient dans n'importe quel anneau unitaire ou algèbre où a est n'importe quel élément inversible . Pour les algèbres de Lie, la définition est légèrement différente.
Voir également
- Antiautomorphisme
- Automorphisme (dans les puzzles Sudoku)
- Sous-groupe caractéristique
- Anneau d'endomorphisme
- Automorphisme de Frobenius
- Morphisme
- Automorphisme d'ordre (en théorie de l'ordre ).
- Automorphisme préservant les relations
- Transformée de Fourier fractionnaire
Les références
- ^ PJ Pahl, R Damrath (2001). "§7.5.5 Automorphismes" . Fondements mathématiques de l'ingénierie informatique (Felix Pahl traduction éd.). Springer. p. 376. ISBN 3-540-67995-2.
- ^ Yale, Paul B. (mai 1966). « Automorphismes des nombres complexes » (PDF) . Revue de Mathématiques . 39 (3) : 135-141. doi : 10.2307/2689301 . JSTOR 2689301 .
- ^ Lounesto, Pertti (2001), Clifford Algebras and Spinors (2e éd.), Cambridge University Press, pp. 22-23, ISBN 0-521-00551-5
- ^ Manuel d'algèbre , 3 , Elsevier , 2003, p. 453
- ^ Sir William Rowan Hamilton (1856). "Mémorandum concernant un nouveau système de racines d'unité" (PDF) . Revue philosophique . 12 : 446.


