Castor occupé - Busy beaver
En informatique théorique , le jeu de castor occupé vise à trouver un programme de terminaison d'une taille donnée qui produit le plus de sortie possible. Puisqu'un programme en boucle sans fin produisant une sortie infinie est facile à concevoir, de tels programmes sont exclus du jeu.
Plus précisément, le jeu du castor occupé consiste à concevoir une machine de Turing à alphabet binaire hésitant qui écrit le plus de 1 sur la bande, en utilisant uniquement un ensemble d'états donné. Les règles du jeu à 2 états sont les suivantes :
- la machine doit avoir deux états en plus de l'état d'arrêt, et
- la bande ne contient initialement que des 0.
Un joueur devrait concevoir une table de transition visant la sortie la plus longue de 1s sur la bande tout en s'assurant que la machine s'arrêtera éventuellement.
Un n ième castor occupé , BB- n ou simplement "castor occupé" est une machine de Turing qui remporte le n- state Busy Beaver Game. C'est-à-dire qu'elle atteint le plus grand nombre de 1 parmi toutes les autres machines de Turing concurrentes à n états possibles . La machine de Turing BB-2 , par exemple, réalise quatre 1 en six étapes.
Déterminer si une machine de Turing arbitraire est un castor occupé est indécidable . Cela a des implications dans la théorie de la calculabilité , le problème de l' arrêt et la théorie de la complexité . Le concept a été introduit pour la première fois par Tibor Radó dans son article de 1962, "On Non-Computable Functions".
Le jeu
Le n -state jeu de castor occupé (ou BB- n jeu ), introduit dans Tibor Radó papier de 1962, implique une classe de machines de Turing , dont chaque membre est tenu de respecter les spécifications de conception suivantes:
- La machine a n états "opérationnels" plus un état Halt, où n est un entier positif, et l'un des n états est distingué comme l'état de départ. (Généralement, les états sont étiquetés par 1, 2, ..., n , avec l'état 1 comme état de départ, ou par A , B , C , ..., avec l'état A comme état de départ.)
- La machine utilise une seule bande infinie (ou illimitée) bidirectionnelle.
- L'alphabet de la bande est {0, 1}, 0 servant de symbole vide.
- La fonction de transition de la machine prend deux entrées :
- l'état actuel de non-arrêt,
- le symbole dans la cellule de bande actuelle,
- et produit trois sorties :
- un symbole pour écraser le symbole dans la cellule de bande courante (il peut s'agir du même symbole que le symbole écrasé),
- une direction de déplacement (gauche ou droite ; c'est-à-dire passer à la cellule de bande un endroit à gauche ou à droite de la cellule actuelle), et
- un état vers lequel effectuer la transition (qui peut être l'état Halt).
- Il y a donc (4 n + 4) 2 n n machines de Turing répondant à cette définition car la forme générale de la formule est ( symboles × directions × ( états + 1)) ( symboles × états ) .
- La fonction de transition peut être vue comme un tableau fini de 5-uplets, chacun de la forme
- (état courant, symbole courant, symbole à écrire, sens de décalage, état suivant).
« Exécuter » la machine consiste à démarrer dans l'état de départ, la cellule de bande actuelle étant n'importe quelle cellule d'une bande vierge (tout-0), puis à itérer la fonction de transition jusqu'à ce que l'état d'arrêt soit entré (le cas échéant). Si, et seulement si, la machine s'arrête finalement, alors le nombre de 1 restant finalement sur la bande est appelé le score de la machine .
Le jeu du castor occupé à n états (BB- n ) est un concours pour trouver une telle machine de Turing à n états ayant le plus grand score possible - le plus grand nombre de 1 sur sa bande après s'être arrêté. Une machine qui atteint le plus grand score possible parmi tous les n machines de Turing -state est appelé un n -state castor occupé, et une machine dont le score est simplement le plus élevé à ce jour atteint (peut - être pas le plus grand possible) est appelé un champion n -state machine.
Radó a exigé que chaque machine inscrite au concours soit accompagnée d'une déclaration du nombre exact de pas qu'elle prend pour atteindre l'état d'arrêt, permettant ainsi de vérifier le score de chaque inscription (en principe) en faisant fonctionner la machine pour le nombre indiqué d'étapes. (Si les entrées devaient consister uniquement en des descriptions de machines, alors le problème de la vérification de chaque entrée potentielle est indécidable, car il équivaut au problème d'arrêt bien connu - il n'y aurait aucun moyen efficace de décider si une machine arbitraire s'arrête finalement.)
Fonctions associées
La fonction castor occupé
La fonction castor occupé quantifie le score maximum atteignable par un castor occupé sur une mesure donnée. Il s'agit d'une fonction non calculable . En outre, une fonction de castor occupée peut croître plus rapidement de manière asymptotique que n'importe quelle fonction calculable.
La fonction de castor occupé, : ℕ → ℕ, est définie de telle sorte que Σ( n ) est le score maximum atteignable (le nombre maximum de 1 finalement sur la bande) parmi toutes les machines de Turing à 2 états n à 2 symboles arrêtées ci- dessus- type décrit, lorsqu'il est démarré sur une bande vierge.
Il est clair que Σ est une fonction bien définie : pour tout n , il y a au plus un nombre fini de machines de Turing à n états comme ci-dessus, à isomorphisme près, donc au plus un nombre fini de temps d'exécution possibles.
Cette séquence infinie Σ est la fonction de castor occupée , et tout n -state machine de Turing de 2 symboles M pour lequel σ ( M ) = Σ ( n ( par exemple, qui atteint le score maximum)) est appelée un castor occupé . Notez que pour chaque n , il existe au moins quatre castors occupés à n états (car, étant donné n'importe quel castor occupé à n états, un autre est obtenu en changeant simplement la direction du décalage dans une transition d'arrêt, un autre en décalant tous les changements de direction à leur opposé , et la finale en décalant la direction d'arrêt du castor occupé tout échangé).
Non-calculabilité
L'article de Radó de 1962 a prouvé que si f : ℕ → ℕ est une fonction calculable , alors Σ( n ) > f(n) pour tout n suffisamment grand , et donc que Σ n'est pas une fonction calculable.
De plus, cela implique qu'il est indécidable par un algorithme général si une machine de Turing arbitraire est un castor occupé. (Un tel algorithme ne peut pas exister, car son existence permettrait de calculer , ce qui est une impossibilité prouvée. En particulier, un tel algorithme pourrait être utilisé pour construire un autre algorithme qui calculerait Σ comme suit : pour tout n donné , chacun des les finiment beaucoup de n -state 2-symbole machines de Turing seraient testées jusqu'à ce qu'un n -state castor occupé se trouve, cette machine de castor occupé serait alors simulé pour déterminer son score, qui est par Σ définition ( n )).
Même si Σ( n ) est une fonction incalculable, il existe des petits n pour lesquels il est possible d'obtenir ses valeurs et de prouver qu'elles sont correctes. Il n'est pas difficile de montrer que Σ(0) = 0, Σ(1) = 1, Σ(2) = 4, et avec de plus en plus de difficultés on peut montrer que Σ(3) = 6 et Σ(4) = 13 (séquence A028444 dans l' OEIS ). Σ( n ) n'a pas encore été déterminé pour aucune instance de n > 4, bien que des limites inférieures aient été établies (voir la section Valeurs connues ci-dessous).
En 2016, Adam Yedidia et Scott Aaronson ont obtenu la première borne supérieure (explicite) sur le minimum n pour lequel Σ( n ) est indémontrable dans ZFC . Pour ce faire, ils ont construit une machine de Turing à 7910 états dont le comportement ne peut pas être prouvé sur la base des axiomes habituels de la théorie des ensembles (théorie des ensembles de Zermelo-Fraenkel avec l' axiome du choix ), sous des hypothèses de cohérence raisonnables ( propriété de Ramsey stationnaire ). Cela a ensuite été réduit à 1919 États, la dépendance à l'égard de la propriété stationnaire de Ramsey étant éliminée, puis à 748 États.
Complexité et non-prouvabilité de Σ
Une variante de la complexité de Kolmogorov est définie comme suit [cf. Boolos, Burgess & Jeffrey, 2007] : La complexité d'un nombre n est le plus petit nombre d'états nécessaires pour une machine de Turing de classe BB qui s'arrête avec un seul bloc de n 1 consécutifs sur une bande initialement vierge. La variante correspondante du théorème d'incomplétude de Chaitin stipule que, dans le contexte d'un système axiomatique donné pour les nombres naturels, il existe un nombre k tel qu'aucun nombre spécifique ne peut être prouvé avoir une complexité supérieure à k , et donc qu'aucune borne supérieure spécifique peut être prouvé pour Σ( k ) (ce dernier est dû au fait que « la complexité de n est supérieure à k » serait prouvée si « n > Σ( k ) » était prouvé). Comme mentionné dans la référence citée, pour tout système axiomatique de « mathématiques ordinaires », la plus petite valeur k pour laquelle cela est vrai est bien inférieure à 10↑↑10 ; par conséquent, dans le contexte des mathématiques ordinaires, ni la valeur ni aucune borne supérieure de Σ(10 10) ne peut être prouvée. ( Le premier théorème d'incomplétude de Gödel est illustré par ce résultat : dans un système axiomatique des mathématiques ordinaires, il existe une phrase vraie mais non démontrable de la forme "Σ(10 10) = n ", et il y a une infinité de vrais- phrases mais non prouvables de la forme "Σ(10 ↑↑ 10) < n ".)
Fonction de décalage maximum S
En plus de la fonction , Radó [1962] a introduit une autre fonction extrême pour la classe BB des machines de Turing, la fonction de décalages maximaux , S , définie comme suit :
- s ( M ) = le nombre de quarts de travail que M effectue avant de s'arrêter, pour tout M dans E n ,
- S ( n ) = max{ s ( M ) | M ∈ E n } = le plus grand nombre de décalages effectués par une machine de Turing à 2 symboles à n états s'arrêtant .
Parce que ces machines de Turing doivent avoir un décalage dans chaque transition ou "étape" (y compris toute transition vers un état Halt), la fonction max-shifts est en même temps une fonction max-steps.
Radó a montré que S est non calculable pour la même raison que Σ est non calculable — il croît plus rapidement que n'importe quelle fonction calculable. Il l'a prouvé simplement en notant que pour chaque n , S ( n ) ≥ Σ( n ). Chaque équipe peut écrire un 0 ou un 1 sur la bande, tandis que compte un sous-ensemble des équipes qui ont écrit un 1, à savoir celles qui n'avaient pas été écrasées au moment où la machine de Turing s'est arrêtée ; par conséquent, S croît au moins aussi vite que , dont il a déjà été prouvé qu'il croît plus vite que n'importe quelle fonction calculable.
La connexion suivante entre Σ et S a été utilisée par Lin & Radó [ Computer Studies of Turing Machine Problems , 1965] pour prouver que Σ(3) = 6 : Pour un n donné , si S ( n ) est connu alors tous les états n Les machines de Turing peuvent (en principe) fonctionner jusqu'à S ( n ) pas, auquel cas toute machine qui ne s'est pas encore arrêtée ne s'arrêtera jamais. À ce stade, en observant quelles machines se sont arrêtées avec le plus de 1 sur la bande (c'est-à-dire les castors occupés), on obtient de leurs bandes la valeur de ( n ). L'approche utilisée par Lin & Radó pour le cas de n = 3 était de conjecturer que S (3) = 21, puis de simuler toutes les machines à 3 états essentiellement différentes jusqu'à 21 étapes. En analysant le comportement des machines qui ne s'étaient pas arrêtées en 21 étapes, ils ont réussi à montrer qu'aucune de ces machines ne s'arrêterait jamais, prouvant ainsi la conjecture que S (3) = 21, et déterminant que (3) = 6 par la procédure qui vient d'être décrite.
Les inégalités entre Σ et S sont les suivantes (d'après [Ben-Amram, et al., 1996]), qui sont valables pour tout n 1 :
et une borne asymptotiquement améliorée (de [Ben-Amram, Petersen, 2002]) : il existe une constante c , telle que pour tout n 2 ,
tend à être proche du carré de , et en fait de nombreuses machines donnent moins que .
Valeurs connues pour et S
Depuis 2016, les valeurs des fonctions pour Σ( n ) et S ( n ) ne sont connues exactement que pour n < 5.
L'actuel (à partir de 2018) champion de castor occupé dans les 5 États produit 4098 1s, en utilisant47 176 870 pas (découverts par Heiner Marxen et Jürgen Buntrock en 1989), mais il reste 18 ou 19 (peut-être moins de 10, voir ci-dessous) des machines au comportement irrégulier dont on pense qu'elles ne s'arrêtent jamais, mais dont il n'a pas été prouvé qu'elles courir à l'infini. Skelet répertorie 42 ou 43 machines non éprouvées, mais 24 sont déjà éprouvées. Les machines restantes ont été simulées à 81,8 milliards de pas, mais aucune ne s'est arrêtée. Daniel Briggs a également prouvé certaines machines. Une autre source indique que 98 machines n'ont pas encore fait leurs preuves. Il y a une analyse des récalcitrants. Ainsi, il est probable que Σ(5) = 4098 et S(5) = 47176870, mais cela reste à prouver, et on ne sait pas s'il reste des réticences (à partir de 2018). À l'heure actuelle, le champion record de 6 États produit plus de3,515 × 10 18 267 1s (exactement (25×4 30341 +23)/9), en utilisant plus7,412 × 10 36 534 marches (trouvées par Pavel Kropitz en 2010). Comme indiqué ci-dessus, ce sont des machines de Turing à 2 symboles.
Une simple extension de la machine à 6 états conduit à une machine à 7 états qui écrira plus de 10 10 10 1018 705 353 1s à la bande, mais il existe sans aucun doute des machines à 7 états beaucoup plus occupées. Cependant, d'autres chasseurs de castors occupés ont différents ensembles de machines.
Milton Green, dans son article de 1964 « A Lower Bound on Rado's Sigma Function for Binary Turing Machines », a construit un ensemble de machines de Turing démontrant que
où ↑ est la notation avec flèche vers le haut de Knuth et A est la fonction d'Ackermann .
Ainsi
(avec 3 3 3 = 7 625 597 484 987 termes dans la tour exponentielle), et
où le nombre g 1 est l'énorme valeur de départ dans la séquence qui définit le nombre de Graham .
En 1964, Milton Green a développé une limite inférieure pour la fonction Busy Beaver qui a été publiée dans les actes du symposium IEEE de 1964 sur la théorie des circuits de commutation et la conception logique. Heiner Marxen et Jürgen Buntrock l'ont décrit comme « une limite inférieure non triviale (pas récursive primitive) ». Cette borne inférieure peut être calculée mais est trop complexe pour être exprimée comme une seule expression en termes de n. Lorsque n=8 la méthode donne Σ(8) ≥ 3 × (7 × 3 92 - 1) / 2 8,248×10 44 .
Il peut être dérivé des limites inférieures actuelles que :
En revanche, la meilleure borne inférieure actuelle (à partir de 2018) sur Σ(6) est 10 18 267 , ce qui est supérieur à la borne inférieure donnée par la formule de Green, 3 3 = 27 (ce qui est minuscule en comparaison). En fait, il est bien supérieur à la borne inférieure : 3 ↑↑ 3 = 3 3 3 =7 625 597 484 987 , qui est la première borne inférieure de Green pour Σ(8), et également bien supérieure à la deuxième borne inférieure : 3×(7×3 92 −1)/2.
Σ(7) est de la même manière beaucoup, beaucoup plus élevé que la limite inférieure commune actuelle 3 31 (près de 618 000 milliards), donc la deuxième limite inférieure est également très, très faible.
Preuve de l'incalculabilité de S ( n ) et ( n )
Supposons que S ( n ) est une fonction calculable et que EvalS désigne une TM, évaluant S ( n ). Étant donné une bande avec n 1, elle produira S ( n ) 1 sur la bande puis s'arrêtera. Soit Clean dénoter une machine de Turing nettoyant la séquence de 1 initialement écrite sur la bande. Soit Double une machine de Turing évaluant la fonction n + n . Étant donné une bande avec n 1s, elle produira 2 n 1s sur la bande puis s'arrêtera. Créons la composition Double | ÉvalS | Clean et soit n 0 le nombre d'états de cette machine. Soit Create_n 0 une machine de Turing créant n 0 1s sur une bande initialement vierge. Cette machine peut être construite de manière triviale pour avoir n états 0 (l'état i écrit 1, déplace la tête vers la droite et passe à l'état i +1, sauf l'état n 0 qui s'arrête). Soit N la somme n 0 + n 0 .
Soit BadS la composition Create_n 0 | Double | ÉvalS | Propre . Notez que cette machine a N états. À partir d'une bande initialement vierge, il crée d'abord une séquence de n 0 1 puis la double, produisant une séquence de N 1 . Ensuite, BadS produira S ( N ) 1 sur la bande, et enfin il effacera tous les 1 puis s'arrêtera. Mais la phase de nettoyage va continuer au moins S ( N ) pas, donc le temps de travail de BadS est strictement supérieur à S ( N ), ce qui contredit la définition de la fonction S ( n ).
L'incalculabilité de Σ( n ) peut être prouvée de la même manière. Dans la preuve ci-dessus, il faut échanger la machine EvalS avec EvalΣ et Clean avec Increment — une simple TM, recherchant un premier 0 sur la bande et le remplaçant par 1.
L'incalculabilité de S ( n ) peut également être établie en référence au problème d'arrêt de la bande vierge. Le problème d'arrêt de la bande vierge est le problème de décider pour n'importe quelle machine de Turing si elle s'arrêtera ou non lorsqu'elle sera démarrée sur une bande vide. Le problème d'arrêt de la bande vierge est équivalent au problème d'arrêt standard et il est donc également incalculable. Si S ( n ) était calculable, alors nous pourrions résoudre le problème d'arrêt de la bande vierge simplement en exécutant n'importe quelle machine de Turing donnée avec n états pour S ( n ) étapes ; s'il ne s'est toujours pas arrêté, il ne s'arrêtera jamais. Ainsi, puisque le problème d'arrêt de la bande vierge n'est pas calculable, il s'ensuit que S ( n ) doit également être incalculable.
Généralisations
Pour tout modèle de calcul, il existe des analogues simples du castor occupé. Par exemple, la généralisation aux machines de Turing à n états et m symboles définit les fonctions de castor occupé généralisées suivantes :
- ( n , m ) : le plus grand nombre de non nuls imprimables par une machine à n états, m -symbole démarrée sur une bande initialement vierge avant de s'arrêter, et
- S ( n , m ): le plus grand nombre de mesures prises par un n -state, m machine à -symbol a commencé sur une bande initialement vierge avant d' arrêter.
Par exemple, la machine à 3 symboles à 3 états la plus ancienne trouvée jusqu'à présent fonctionne 119 112 334 170 342 540 pas avant de s'arrêter. La plus longue machine à 6 états et 2 symboles qui a la propriété supplémentaire d'inverser la valeur de la bande à chaque étape produit6147 1s après47 339 970 marches. Alors S RTM (6) ≥47 339 970 et RTM (6) ≥6147 .
Il est possible de généraliser davantage la fonction de castor occupé en l'étendant à plus d'une dimension.
De même, nous pourrions définir une fonction analogue à la fonction pour les machines à registres comme le plus grand nombre pouvant être présent dans n'importe quel registre à l'arrêt, pour un nombre donné d'instructions.
Valeurs exactes et bornes inférieures
Le tableau suivant répertorie les valeurs exactes et certaines limites inférieures connues pour S ( n , m ) et ( n , m ) pour les problèmes généralisés de castor occupé. Remarque : entrées répertoriées comme " ?" sont délimités d'en bas par le maximum de toutes les entrées à gauche et au-dessus. Ces machines n'ont pas été étudiées ou ont été par la suite dépassées par une machine plus petite.
Les machines de Turing qui atteignent ces valeurs sont disponibles sur la page web de Pascal Michel . Chacun de ces sites Web contient également des analyses des machines de Turing et des références aux preuves des valeurs exactes.
Valeurs de S( n , m ) mm2-état 3-état 4 états 5-état 6-état 7-état 2-symbole 6 21 107 47 176 870 ? > 7,4 × 10 36 534 > 10 10 10 1018 705 353 3-symbole 38 ?? 119 112 334 170 342 540 > 1,0 × 10 14 072 ? ? ? 4-symbole ?? 3 932 964 > 5,2 × 10 13 036 ? ? ? ? 5-symbole > 1,9 × 10 704 ? ? ? ? ? 6-symbole > 2,4 × 10 9866 ? ? ? ? ? Valeurs de ( n , m ) mm2-état 3-état 4 états 5-état 6-état 7-état 2-symbole 4 6 13 4098 ? > 3,5 × 10 18 267 > 10 10 10 1018 705 353 3-symbole 9 ?? 374 676 383 > 1,3 × 10 7036 ? ? ? 4-symbole ?? 2050 > 3,7 × 10 6518 ? ? ? ? 5-symbole > 1,7 × 10 352 ? ? ? ? ? 6-symbole > 1,9 × 10 4933 ? ? ? ? ?
Machines de Turing non déterministes
| p | pas | États |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 6 | 7 |
| 4 | 7 | 11 |
| 5 | 8 | 15 |
| 6 | 7 | 18 |
| 7 | 6 | 18 |
Le problème peut être étendu aux machines de Turing non déterministes en recherchant le système avec le plus grand nombre d'états dans toutes les branches ou la branche avec le plus grand nombre d'étapes. La question de savoir si un NDTM donné s'arrêtera est toujours irréductible du point de vue du calcul, et le calcul requis pour trouver un castor NDTM occupé est nettement supérieur au cas déterministe, car plusieurs branches doivent être prises en compte. Pour un système à 2 états et 2 couleurs avec p cas ou règles, le tableau de droite donne le nombre maximum d'étapes avant l'arrêt et le nombre maximum d'états uniques créés par le NDTM.
Applications
En plus de poser un jeu mathématique plutôt difficile , les fonctions de castor occupées offrent une toute nouvelle approche pour résoudre des problèmes de mathématiques pures. De nombreux problèmes ouverts en mathématiques pourraient en théorie, mais pas en pratique, être résolus de manière systématique étant donné la valeur de S ( n ) pour un n suffisamment grand .
Considérez toute conjecture qui pourrait être réfutée via un contre - exemple parmi un nombre dénombrable de cas (par exemple la conjecture de Goldbach ). Écrivez un programme informatique qui teste séquentiellement cette conjecture pour des valeurs croissantes. Dans le cas de la conjecture de Goldbach, nous considérerions séquentiellement chaque nombre pair 4 et testerions s'il s'agit ou non de la somme de deux nombres premiers. Supposons que ce programme soit simulé sur une machine de Turing à n états. S'il trouve un contre-exemple (un nombre pair 4 qui n'est pas la somme de deux nombres premiers dans notre exemple), il s'arrête et l'indique. Cependant, si la conjecture est vraie, alors notre programme ne s'arrêtera jamais. (Ce programme ne s'arrête que s'il trouve un contre-exemple.)
Maintenant, ce programme est simulé par une machine de Turing à n états, donc si nous connaissons S ( n ), nous pouvons décider (dans un laps de temps fini) s'il s'arrêtera ou non en exécutant simplement la machine autant d'étapes. Et si, après S ( n ) pas, la machine ne s'arrête pas, nous savons qu'elle ne s'arrêtera jamais et donc qu'il n'y a pas de contre-exemples à la conjecture donnée (c'est-à-dire pas de nombres pairs qui ne soient pas la somme de deux nombres premiers). Cela prouverait que la conjecture est vraie.
Ainsi, des valeurs spécifiques (ou des limites supérieures) pour S ( n ) pourraient être utilisées pour résoudre systématiquement de nombreux problèmes ouverts en mathématiques (en théorie). Cependant, les résultats actuels sur le problème du castor occupé suggèrent que cela ne sera pas pratique pour deux raisons :
- Il est extrêmement difficile de prouver des valeurs pour la fonction de castor occupé (et la fonction de décalage maximum). Cela n'a été prouvé que pour des machines extrêmement petites avec moins de cinq états, alors qu'il faudrait vraisemblablement au moins 20 à 50 états pour faire une machine utile. De plus, chaque valeur exacte connue de S ( n ) a été prouvée en énumérant chaque machine de Turing à n états et en prouvant si chacune s'arrête ou non. Il faudrait calculer S ( n ) par une méthode moins directe pour que cela soit réellement utile.
- Mais même si l'on trouvait un meilleur moyen de calculer S ( n ), les valeurs de la fonction de castor occupé (et de la fonction max shift) deviennent très grandes, très rapidement. S (6) > 1036 534 nécessite déjà une accélération spéciale basée sur un modèle pour pouvoir simuler jusqu'à la fin. De même, nous savons que S (10) > Σ(10) > 3 3 est un nombre gigantesque et S (17) > Σ(17) > G, où G est le nombre de Graham - un nombre énorme. Ainsi, même si nous connaissions, disons, S (30), il est totalement déraisonnable de faire fonctionner n'importe quelle machine ce nombre d'étapes. Il n'y a pas assez de capacité de calcul dans la partie connue de l'univers pour avoir effectué même S (6) opérations directement.
Instances notables
Une machine de Turing binaire à 748 états a été construite qui s'arrête si ZFC est incohérent. Une machine de Turing à 744 états a été construite qui s'arrête si l' hypothèse de Riemann est fausse. Une machine de Turing à 43 états a été construite qui arrête si la conjecture de Goldbach est fausse, et une machine à 27 états pour cette conjecture a été proposée mais pas encore vérifiée.
Une machine de Turing à 15 états a été construite qui arrête ssi la conjecture suivante formulée par Paul Erdős en 1979 est fausse : pour tout n > 8, il y a au moins un chiffre 2 dans la représentation en base 3 de 2 n .
Exemples
Ce sont des tables de règles pour les machines de Turing qui génèrent Σ(1) et S (1), Σ(2) et S (2), Σ(3) (mais pas S (3)), Σ(4) et S (4), et la borne inférieure la plus connue pour (5) et S (5), et Σ(6) et S (6). Pour d'autres visualisations,
Dans les tableaux, les colonnes représentent l'état actuel et les lignes représentent le symbole actuel lu sur la bande. Chaque entrée du tableau est une chaîne de trois caractères, indiquant le symbole à écrire sur la bande, la direction à suivre et le nouvel état (dans cet ordre). L'état d'arrêt est représenté par H .
Chaque machine commence dans l'état A avec une bande infinie qui ne contient que des 0. Ainsi, le symbole initial lu sur la bande est un 0.
Résultat clé: (commence à la position surligné , arrête à la position souligné )
Castor occupé à 1 état et 2 symboles UNE 0 1R H 1 (non utilisé)
Résultat : 0 0 1 0 0 (1 étape, un "1" au total)
Castor occupé à 2 états et 2 symboles UNE B 0 1R B 1L A 1 1L B 1R H
Résultat : 0 0 1 1 1 1 0 0 (6 étapes, quatre "1" au total)
Castor occupé à 3 états et 2 symboles UNE B C 0 1R B 0R C 1L C 1 1R H 1R B 1L A
Résultat : 0 0 1 1 1 1 1 1 0 0 (14 étapes, six "1" au total).
Contrairement aux machines précédentes, celle-ci est un castor occupé uniquement pour Σ, mais pas pour S . ( S (3) = 21.)
Castor occupé à 4 états et 2 symboles UNE B C ré 0 1R B 1L A 1R H 1R D 1 1L B 0L C 1L D 0R A
Résultat : 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 (107 étapes, treize "1" au total)
Meilleur concurrent actuel à 5 états et 2 symboles (castor occupé possible) UNE B C ré E 0 1R B 1R C 1R D 1L A 1R H 1 1L C 1R B 0L E 1L D 0L A
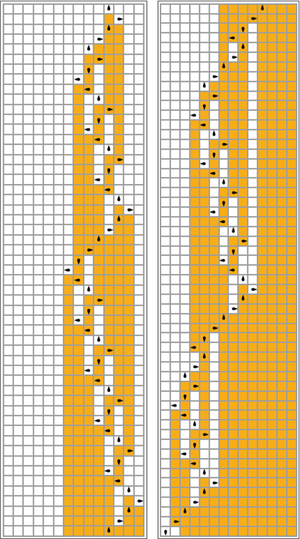
Résultat : 4098 "1" avec 8191 "0" entrecoupés en 47 176 870 pas.
Notez dans l'image de droite comment cette solution est similaire qualitativement à l'évolution de certains automates cellulaires .
meilleur concurrent actuel à 6 états et 2 symboles UNE B C ré E F 0 1R B 1R C 1L D 1R E 1L A 1L H 1 1L E 1R F 0R B 0L C 0R D 1R C
Résultat : ≈3,515 × 10 18267 "1"s par ≈ 7,412 × 10 36534 pas.
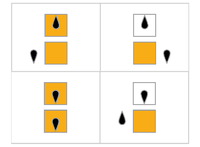
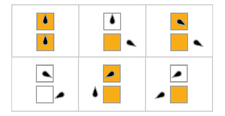
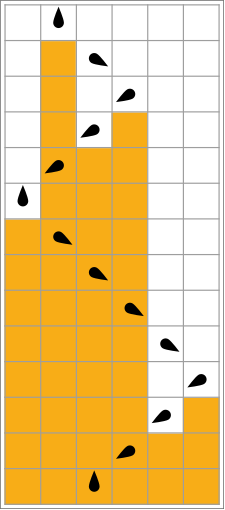
Visualisations
Dans le tableau suivant, les règles pour chaque castor occupé (en maximisant ) sont représentées visuellement, avec des carrés oranges correspondant à un "1" sur la bande, et des blancs correspondant à "0". La position de la tête est indiquée par l'ovoïde noir, l'orientation de la tête représentant l'état. Les bandes individuelles sont disposées horizontalement, le temps progressant verticalement. L'état d'arrêt est représenté par une règle qui mappe un état sur lui-même (la tête ne bouge pas).
Voir également
Remarques
- ^ un b Radó, Tibor (mai 1962). "Sur les fonctions non calculables" (PDF) . Journal technique du système Bell . 41 (3) : 877-884. doi : 10.1002/j.1538-7305.1962.tb00480.x .
- ^ Chaitin (1987)
- ^ Adam Yedidia et Scott Aaronson (mai 2016). Une machine de Turing relativement petite dont le comportement est indépendant de la théorie des ensembles (Rapport technique). MIT. arXiv : 1605.04343 . Bibcode : 2016arXiv160504343Y .
- ^ Aron, Jacob. "Cette machine de Turing devrait fonctionner indéfiniment à moins que les maths ne soient erronées" . Récupéré le 2016-09-25 .
- ^ une version b du 3 mai contenait 7918 états : "Le 8000ème nombre Busy Beaver échappe à la théorie des ensembles ZF" . Blog optimisé pour Shtetl . 2016-05-03 . Récupéré le 2016-09-25 .
- ^ A b c "Trois annonces" . Blog optimisé pour Shtetl . 2016-05-03 . Récupéré le 2018-04-27 .
- ^ "GitHub - sorear/metamath-turing-machines: énumérateurs de preuve Metamath et autres choses" . 2019-02-13.
- ^ "La frontière occupée du castor" (PDF) .
- ^ "Page squelette pour le problème Busy Beaver" . squelet.ludost.net .
- ^ Turing: Un projet pour terminer le castor occupé de 5
- ^ "Le problème du castor occupé : UNE NOUVELLE ATTAQUE DU MILLÉNAIRE" .
- ^ un b Wolfram, Stephen (4 février 2021). "Machines de Turing à plusieurs voies" . www.wolframphysics.org .
- ^ Chaitin 1987
- ^ Lloyd 2001. Capacité de calcul de l'univers .
- ^ A b c Pavlus, John (10 Décembre 2020). "Comment les programmes informatiques les plus lents éclairent les limites fondamentales des mathématiques" . Magazine Quanta . Récupéré le 2020-12-11 .
- ^ Tristan Stérin et Damien Woods (juillet 2021). Sur la difficulté de connaître les valeurs de castor occupé BB(15) et BB(5,4) (Rapport technique). Université de Maynooth. arXiv : 2107.12475 .
- ^ Erdõs, Paul (1979). "Quelques problèmes non conventionnels en théorie des nombres" . Math. Mag. 52 (2) : 67-70. doi : 10.1080/0025570X.1979.11976756 .
- ^ Lin, Shen; Rado, Tibor (avril 1965). "Etudes informatiques des problèmes de la machine de Turing" . Journal de l'ACM . 12 (2) : 196-212. doi : 10.1145/321264.321270 . S2CID 17789208 .
Les références
-
Radó, Tibor (mai 1962). "Sur les fonctions non calculables" (PDF) . Journal technique du système Bell . 41 (3) : 877-884. doi : 10.1002/j.1538-7305.1962.tb00480.x .
- C'est là que Radó a défini pour la première fois le problème du castor occupé et a prouvé qu'il était incalculable et qu'il se développait plus rapidement que n'importe quelle fonction calculable.
-
Lin, Shen ; Radó, Tibor (avril 1965). "Études informatiques des problèmes de la machine de Turing" . Journal de l'ACM . 12 (2) : 196-212. doi : 10.1145/321264.321270 . S2CID 17789208 .
- Les résultats de cet article étaient déjà apparus en partie dans la thèse de doctorat de Lin en 1963, sous la direction de Radó. Lin & Radó prouvent que Σ(3) = 6 et S (3) = 21 en prouvant que toutes les machines de Turing à 3 états et 2 symboles qui ne s'arrêtent pas dans les 21 étapes ne s'arrêteront jamais. (La plupart sont prouvés automatiquement par un programme informatique, mais 40 sont prouvés par une inspection humaine.)
-
Brady, Allen H. (avril 1983). "La détermination de la valeur de la fonction non calculable de Rado ( k ) pour les machines de Turing à quatre états" . Mathématiques du calcul . 40 (162) : 647-665. doi : 10.1090/S0025-5718-1983-0689479-6 . JSTOR 2007539 .
- Brady prouve que Σ(4) = 13 et S (4) = 107. Brady définit deux nouvelles catégories pour les machines de Turing à 3 états et 2 symboles non-arrêtantes : les sapins de Noël et les compteurs. Il utilise un programme informatique pour prouver que toutes les machines sauf 27 qui exécutent plus de 107 étapes sont des variantes d'arbres de Noël et de compteurs dont on peut prouver qu'elles fonctionnent à l'infini. Les 27 dernières machines (appelées réfractaires) sont prouvées par une inspection personnelle par Brady lui-même pour ne pas s'arrêter.
-
Machlin, Rona; Stout, Quentin F. (juin 1990). "Le comportement complexe des machines simples" . Physica D : Phénomènes non linéaires . 42 (1–3) : 85–98. Bibcode : 1990PhyD ... 42 ... 85M . doi : 10.1016/0167-2789(90)90068-Z . hdl : 2027,42/28528 .
- Machlin et Stout décrivent le problème du castor occupé et de nombreuses techniques utilisées pour trouver des castors occupés (qu'ils appliquent aux machines de Turing avec 4 états et 2 symboles, vérifiant ainsi la preuve de Brady). Ils suggèrent comment estimer une variante de la probabilité d'arrêt de Chaitin (Ω).
-
Marxen, Heiner ; Buntrock, Jürgen (février 1990). "Attaquer le Busy Beaver 5" . Bulletin de l'EATCS . 40 : 247-251. Archivé de l'original le 2006-10-09 . Récupéré le 2020-01-19 .
- Marxen et Buntrock démontrent que Σ(5) ≥ 4098 et S (5) ≥ 47 176 870 et décrivent en détail la méthode qu'ils ont utilisée pour trouver ces machines et prouver que beaucoup d'autres ne s'arrêteront jamais.
-
Vert, Milton W. (1964). Une limite inférieure sur la fonction Sigma de Rado pour les machines de Turing binaires . 1964 Actes du cinquième symposium annuel sur la théorie des circuits de commutation et la conception logique . p. 91-94. doi : 10.1109/SWCT.1964.3 .
- Green construit récursivement des machines pour un nombre quelconque d'états et fournit la fonction récursive qui calcule leur score (calcule σ), fournissant ainsi une borne inférieure pour Σ. La croissance de cette fonction est comparable à celle de la fonction d' Ackermann .
-
Dewdney, Alexander K. (1984). "Un piège informatique pour le castor occupé, la machine de Turing la plus travaillante". Scientifique américain . 251 (2) : 10-17.
- Les programmes occupés par les castors sont décrits par Alexander Dewdney dans Scientific American , août 1984, pages 19-23, également mars 1985 p. 23 et avril 1985 p. 30 .
- Chaitin, Gregory J. (1987). « Calcul de la fonction de castor occupé » (PDF) . En couverture, TM; Gopinath, B. (éd.). Problèmes ouverts de communication et de calcul . Springer. p. 108-112. ISBN 978-0-387-96621-2.
-
Brady, Allen H. (1995). "Le jeu de castor occupé et le sens de la vie". Dans Herken, Rolf (éd.). La Machine de Turing universelle : Une enquête d'un demi-siècle (2e éd.). Vienne, New York : Springer-Verlag. p. 237-254. ISBN 978-3-211-82637-9.
- Dans lequel Brady (de renommée dans 4 états) décrit une certaine histoire de la bête et appelle sa poursuite "The Busy Beaver Game". Il décrit d'autres jeux (par exemple les automates cellulaires et le jeu de la vie de Conway ). D'un intérêt particulier est "The Busy Beaver Game in Two Dimensions" (p. 247). Avec 19 références.
-
Booth, Taylor L. (1967). Machines séquentielles et théorie des automates . New York : Wiley. ISBN 978-0-471-08848-6.
- Cf chapitre 9, Machines de Turing. Un livre difficile, destiné aux ingénieurs électriciens et aux spécialistes techniques. Discute de la récursivité, de la récursivité partielle en référence aux machines de Turing, du problème d'arrêt. Une référence dans Booth attribue le castor occupé à Rado. Booth définit également le problème du castor occupé de Rado dans les "problèmes domestiques" 3, 4, 5, 6 du chapitre 9, p. 396. Le problème 3 consiste à « montrer que le problème du castor occupé est insoluble... pour toutes les valeurs de n ».
-
Ben-Amram, AM ; Julström, BA ; Zwick, U. (1996). "Une note sur les castors occupés et autres créatures" . Théorie des systèmes mathématiques . 29 (4) : 375-386. CiteSeerX 10.1.1.75.1297 . doi : 10.1007/BF01192693 . S2CID 30937913 .
- Bornes entre les fonctions et S .
-
Ben-Amram, AM ; Petersen, H. (2002). « Amélioration des limites pour les fonctions liées aux castors occupés ». Théorie des systèmes informatiques . 35 : 1–11. CiteSeerX 10.1.1.136.5997 . doi : 10.1007/s00224-001-1052-0 . S2CID 10429773 .
- Limites améliorées.
-
Lafitte, G.; Papazian, C. (juin 2007). "Le tissu des petites machines de Turing". Calcul et logique dans le monde réel, Actes de la troisième conférence sur la calculabilité en Europe . p. 219-227. CiteSeerX 10.1.1.104.3021 .
- Cet article contient une classification complète des machines de Turing à 2 états et 3 symboles, et donc une preuve pour le castor occupé (2, 3) : Σ(2, 3) = 9 et S(2, 3) = 38.
- Boolos, George S.; Burgess, John P.; Jeffrey, Richard C. (2007). Calculabilité et logique (cinquième éd.). La presse de l'Universite de Cambridge. ISBN 978-0-521-87752-7.
-
Kropitz, Pavel (2010). Problém Busy Beaver (thèse de licence) (en slovaque). Université Charles de Prague.
- Il s'agit de la description des idées, des algorithmes et de leur mise en œuvre, avec la description des expériences examinant des machines de Turing à 5 et 6 états en parallèle sur 31 ordinateurs à 4 cœurs et enfin les meilleurs résultats pour la MT à 6 états.
Liens externes
- La page de Heiner Marxen , qui, avec Jürgen Buntrock, a trouvé les enregistrements mentionnés ci-dessus pour une machine de Turing à 5 et 6 états.
- Enquête historique de Pascal Michel sur les résultats des castors occupés qui contient également les meilleurs résultats et quelques analyses.
- Définition de la classe RTM - Reversal Turing Machines, sous-classe simple et forte des TM.
- Le " Millennium Attack " au Rensselaer RAIR Lab sur le problème du castor occupé. Cet effort a permis de trouver plusieurs nouveaux records et d'établir plusieurs valeurs pour la quadruple formalisation.
- Archives du site Web et forum de Daniel Briggs pour résoudre le problème du castor occupé à 5 états et 2 symboles, basé sur la liste des machines non régulières de Skelet (Georgi Georgiev).
- Aaronson, Scott (1999), Qui peut nommer le plus grand nombre ?
- Weisstein, Eric W. "Castor Occupé" . MathWorld .
- Busy Beaver Turing Machines - Computerphile
- Pascal Michel. Le concours Busy Beaver : une enquête historique . 70 pages. 2017. <hal-00396880v5>