Fonction convexe - Convex function

Fonction convexe sur un intervalle.

Une fonction (en noir) est convexe si et seulement si la région au-dessus de son graphique (en vert) est un ensemble convexe .

Un graphique de la fonction convexe bivariée x ² + xy + y ² .

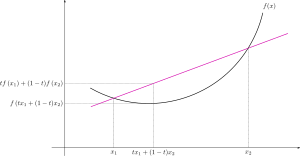
En mathématiques , une fonction à valeur réelle est appelée convexe si le segment de droite entre deux points quelconques sur le graphique de la fonction ne se trouve pas en dessous du graphique entre les deux points. De manière équivalente, une fonction est convexe si son épigraphe (l'ensemble des points sur ou au-dessus du graphique de la fonction) est un ensemble convexe . Une fonction deux fois différentiable d'une seule variable est convexe si et seulement si sa dérivée seconde est non négative sur tout son domaine. Des exemples bien connus de fonctions convexes d'une seule variable incluent la fonction quadratique et la fonction exponentielle${\style d'affichage x^{2}}$ ${\style d'affichage e^{x}}$. En termes simples, une fonction convexe fait référence à une fonction qui a la forme d'une tasse , et une fonction concave a la forme d'un capuchon . ${\displaystyle \cup }$${\displaystyle \cap }$

Les fonctions convexes jouent un rôle important dans de nombreux domaines des mathématiques. Ils sont particulièrement importants dans l'étude des problèmes d' optimisation où ils se distinguent par un certain nombre de propriétés pratiques. Par exemple, une fonction strictement convexe sur un ouvert n'a pas plus d'un minimum. Même dans les espaces de dimension infinie, sous des hypothèses supplémentaires appropriées, les fonctions convexes continuent de satisfaire de telles propriétés et, par conséquent, ce sont les fonctionnelles les mieux comprises dans le calcul des variations . En théorie des probabilités , une fonction convexe appliquée à la valeur attendue d'une variable aléatoire est toujours limitée au-dessus par la valeur attendue de la fonction convexe de la variable aléatoire. Ce résultat, connu sous le nom d'inégalité de Jensen , peut être utilisé pour déduire des inégalités telles que l' inégalité moyenne arithmétique-géométrique et l'inégalité de Hölder .

Définition

Lire les médias

Visualiser une fonction convexe et l'inégalité de Jensen

Soit un sous - ensemble convexe d'un espace vectoriel réel et soit une fonction. ${\style d'affichage X}$${\displaystyle f:X\to \mathbb {R} }$

Alors est dit convexe si et seulement si l'une des conditions équivalentes suivantes est vérifiée : ${\style d'affichage f}$

1. Pour toutes et tous : ${\style d'affichage 0\leq t\leq 1}$${\displaystyle x_{1},x_{2}\in X}$
   $${\displaystyle f\left(tx_{1}+(1-t)x_{2}\right)\leq tf\left(x_{1}\right)+(1-t)f\left(x_{2 }\droit)}$$

   
   Le côté droit représente la ligne droite entre et dans le graphique de en fonction de l' augmentation de à ou de la diminution de à balaie cette ligne. De même, l'argument de la fonction dans le côté gauche représente la ligne droite entre et dans ou l' axe - du graphique de Donc, cette condition exige que la ligne droite entre n'importe quelle paire de points sur la courbe de soit au-dessus ou juste rencontre le graphique. ${\displaystyle \left(x_{1},f\left(x_{1}\right)\right)}$${\displaystyle \left(x_{2},f\left(x_{2}\right)\right)}$${\style d'affichage f}$${\style d'affichage t;}$${\style d'affichage t}$${\style d'affichage 0}$${\style d'affichage 1}$${\style d'affichage t}$${\style d'affichage 1}$${\style d'affichage 0}$${\style d'affichage f}$${\style d'affichage x_{1}}$${\style d'affichage x_{2}}$${\style d'affichage X}$${\style d'affichage x}$${\style d'affichage f.}$${\style d'affichage f}$
2. Pour toutes et tous tels que : ${\style d'affichage 0<t<1}$${\displaystyle x_{1},x_{2}\in X}$${\style d'affichage x_{1}\neq x_{2}}$
   $${\displaystyle f\left(tx_{1}+(1-t)x_{2}\right)\leq tf\left(x_{1}\right)+(1-t)f\left(x_{2 }\droit)}$$

   
   La différence de cette deuxième condition par rapport à la première condition ci-dessus est que cette condition n'inclut pas les points d'intersection (par exemple, et ) entre la droite passant par une paire de points sur la courbe de (la droite est représentée par le côté droit de cette condition) et la courbe de la première condition inclut les points d'intersection au fur et à mesure qu'elle devient ou à ou ou En fait, les points d'intersection n'ont pas besoin d'être considérés dans une condition de convexe en utilisant${\displaystyle \left(x_{1},f\left(x_{1}\right)\right)}$${\displaystyle \left(x_{2},f\left(x_{2}\right)\right)}$${\style d'affichage f}$${\style d'affichage f;}$${\displaystyle f\left(x_{1}\right)\leq f\left(x_{1}\right)}$${\displaystyle f\left(x_{2}\right)\leq f\left(x_{2}\right)}$${\style d'affichage t=0}$${\style d'affichage 1,}$${\style d'affichage x_{1}=x_{2}.}$
   $${\displaystyle f\left(tx_{1}+(1-t)x_{2}\right)\leq tf\left(x_{1}\right)+(1-t)f\left(x_{2 }\droit)}$$

   
   parce que et sont toujours vrais (donc pas utile de faire partie d'une condition). ${\displaystyle f\left(x_{1}\right)\leq f\left(x_{1}\right)}$${\displaystyle f\left(x_{2}\right)\leq f\left(x_{2}\right)}$

La deuxième instruction caractérisant les fonctions convexes qui sont valorisées dans la ligne réelle est également l'instruction utilisée pour définir les fonctions convexes qui sont valorisées dans la ligne des nombres réels étendus où une telle fonction est autorisée (mais n'est pas obligée de) prendre comme valeur. La première instruction n'est pas utilisée car elle permet de prendre ou comme valeur, auquel cas, if ou respectivement, alors serait indéfini (car les multiplications et sont indéfinies). La somme est également indéfinie, de sorte qu'une fonction à valeur réelle étendue convexe n'est généralement autorisée à prendre exactement qu'une valeur parmi et comme valeur. ${\displaystyle \mathbb {R} }$ ${\displaystyle [-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \},}$${\style d'affichage f}$${\displaystyle \pm \infty }$${\style d'affichage t}$${\style d'affichage 0}$${\style d'affichage 1}$${\displaystyle f\left(x_{1}\right)=\pm \infty }$${\displaystyle f\left(x_{2}\right)=\pm \infty ,}$${\displaystyle tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)}$${\displaystyle 0\cdot \infty }$${\displaystyle 0\cdot (-\infty )}$${\style d'affichage -\infty +\infty }$${\displaystyle -\infty }$${\style d'affichage +\infty }$

Le deuxième énoncé peut aussi être modifié pour obtenir la définition de la convexité stricte , où cette dernière est obtenue en remplaçant par l'inégalité stricte. Explicitement, l'application est dite strictement convexe si et seulement si pour tout réel et tout tel que : ${\style d'affichage \,\leq \,}$${\style d'affichage \,<.}$${\style d'affichage f}$${\style d'affichage 0<t<1}$${\displaystyle x_{1},x_{2}\in X}$${\style d'affichage x_{1}\neq x_{2}}$

$${\displaystyle f\left(tx_{1}+(1-t)x_{2}\right)<tf\left(x_{1}\right)+(1-t)f\left(x_{2} \droit)}$$

Une fonction strictement convexe est une fonction selon laquelle la ligne droite entre n'importe quelle paire de points sur la courbe est au-dessus de la courbe, à l' exception des points d'intersection entre la ligne droite et la courbe. ${\style d'affichage f}$${\style d'affichage f}$${\style d'affichage f}$

La fonction est dite concave (resp. strictement concave ) si ( multiplié par -1) est convexe (resp. strictement convexe ). ${\style d'affichage f}$${\style d'affichage -f}$${\style d'affichage f}$

Nommage alternatif

Le terme convexe est souvent appelé convexe vers le bas ou concave vers le haut , et le terme concave est souvent appelé concave vers le bas ou convexe vers le haut . Si le terme « convexe » est utilisé sans mot-clé « haut » ou « bas », alors il se réfère strictement à un graphique en forme de coupe . À titre d'exemple, l'inégalité de Jensen fait référence à une inégalité impliquant une fonction convexe ou convexe (vers le haut). ${\displaystyle \cup }$

Propriétés

De nombreuses propriétés de fonctions convexes ont la même formulation simple pour les fonctions de plusieurs variables que pour les fonctions d'une variable. Voir ci-dessous les propriétés pour le cas de plusieurs variables, car certaines d'entre elles ne sont pas répertoriées pour les fonctions d'une variable.

Fonctions d'une variable

• Supposons que est une fonction d'une variable réelle définie sur un intervalle, et laissez${\style d'affichage f}$
  $${\displaystyle R(x_{1},x_{2})={\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}}$$

  
  (notez que c'est la pente de la ligne violette dans le dessin ci-dessus ; la fonction R est symétrique en signifie que R ne change pas en échangeant et ). est convexe si et seulement si est monotone non décroissante en pour chaque fixe (ou vice versa). Cette caractérisation de la convexité est assez utile pour prouver les résultats suivants.${\style d'affichage R(x_{1},x_{2})}$${\style d'affichage (x_{1},x_{2}),}$${\style d'affichage x_{1}}$${\style d'affichage x_{2}}$${\style d'affichage f}$${\style d'affichage R(x_{1},x_{2})}$${\style d'affichage x_{1},}$${\style d'affichage x_{2}}$
• Une fonction convexe d'une variable réelle définie sur un intervalle ouvert C est continue sur admet des dérivées gauche et droite , et celles-ci sont monotones non décroissantes . En conséquence, est dérivable du tout mais au plus dénombrable de nombreux points, l'ensemble sur lequel n'est pas dérivable peut cependant être encore dense. Si est fermé, alors peut ne pas être continu aux extrémités de (un exemple est montré dans la section exemples ).${\style d'affichage f}$ ${\style d'affichage C.}$ ${\style d'affichage f}$${\style d'affichage f}$${\style d'affichage f}$${\style d'affichage C}$${\style d'affichage f}$${\style d'affichage C}$
• Une fonction différentiable d'une variable est convexe sur un intervalle si et seulement si sa dérivée est monotone non décroissante sur cet intervalle. Si une fonction est dérivable et convexe alors elle est aussi continûment dérivable .
• Une fonction dérivable d'une variable est convexe sur un intervalle si et seulement si son graphe est au dessus de toutes ses tangentes :
  $${\style d'affichage f(x)\geq f(y)+f'(y)(xy)}$$

  
  pour tout x et y dans l'intervalle.
• Une fonction deux fois dérivable d'une variable est convexe sur un intervalle si et seulement si sa dérivée seconde y est non négative ; cela donne un test pratique de convexité. Visuellement, une fonction convexe deux fois différentiable "se courbe vers le haut", sans aucune courbure dans l'autre sens ( points d'inflexion ). Si sa dérivée seconde est positive en tous points, alors la fonction est strictement convexe, mais l' inverse n'est pas vrai. Par exemple, la dérivée seconde de est , qui est nulle pour mais est strictement convexe. ${\style d'affichage f(x)=x^{4}}$${\style d'affichage f''(x)=12x^{2}}$${\style d'affichage x=0,}$${\style d'affichage x^{4}}$
  • Cette propriété et la propriété ci-dessus en termes de "... sa dérivée est monotone non décroissante..." ne sont pas égales car si est non négatif sur un intervalle alors est monotone non décroissant sur alors que sa réciproque n'est pas vraie, par exemple, est monotone non décroissant sur tandis que sa dérivée n'est pas définie à certains points sur .${\style d'affichage f''}$${\style d'affichage X}$${\style d'affichage f'}$${\style d'affichage X}$${\style d'affichage f'}$${\style d'affichage X}$${\style d'affichage f''}$${\style d'affichage X}$
• Si est une fonction convexe d'une variable réelle, et , alors est superadditive sur les réels positifs , c'est-à-dire pour les nombres réels positifs et .${\style d'affichage f}$${\style d'affichage f(0)\leq 0}$${\style d'affichage f}$${\style d'affichage f(a+b)\geq f(a)+f(b)}$${\style d'affichage a}$${\style d'affichage b}$

Preuve

Puisque est convexe, en utilisant l'une des définitions de fonction convexe ci-dessus et en laissant s'ensuivre que pour tout réel${\style d'affichage f}$${\style d'affichage x_{2}=0,}$${\style d'affichage 0\leq t\leq 1,}$ $${\displaystyle f(tx_{1})=f(tx_{1}+(1-t)\cdot 0)\leq tf(x_{1})+(1-t)f(0)\leq tf( x_{1})\rightarrow f(tx_{1})\leq tf(x_{1}).}$$ De là il s'ensuit que $${\displaystyle f(a)+f(b)=f\gauche((a+b){\frac {a}{a+b}}\droit)+f\gauche((a+b){\frac {b}{a+b}}\right)\leq {\frac {a}{a+b}}f(a+b)+{\frac {b}{a+b}}f(a+b )=f(a+b)\flèche droite f(a)+f(b)\leq f(a+b).}$$

• Une fonction est convexe au milieu d'un intervalle si pour tout${\style d'affichage C}$${\displaystyle x_{1},x_{2}\en C}$
  $${\displaystyle f\left({\frac {x_{1}+x_{2}}{2}}\right)\leq {\frac {f(x_{1})+f(x_{2})} {2}}.}$$

  
  Cette condition n'est que légèrement plus faible que la convexité. Par exemple, une fonction mesurable de Lebesgue à valeur réelle qui est convexe médiane est convexe : c'est un théorème de Sierpinski . En particulier, une fonction continue qui est convexe au milieu sera convexe.

Fonctions de plusieurs variables

• Une fonction valorisée dans les nombres réels étendus est convexe si et seulement si son épigraphe${\displaystyle f:X\to [-\infty ,\infty ]}$ ${\displaystyle [-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \}}$
  $${\displaystyle \{(x,r)\in X\times \mathbb {R} ~:~r\geq f(x)\}}$$

  
  est un ensemble convexe.
• Une fonction différentiable définie sur un domaine convexe est convexe si et seulement si est valable pour tout dans le domaine.${\style d'affichage f}$${\displaystyle f(x)\geq f(y)+\nabla f(y)\cdot (xy)}$${\style d'affichage x,y}$
• Une fonction deux fois différentiable de plusieurs variables est convexe sur un ensemble convexe si et seulement si sa matrice hessienne de dérivées partielles secondes est semi-définie positive à l'intérieur de l'ensemble convexe.
• Pour une fonction convexe, les ensembles de sous-niveaux et avec sont des ensembles convexes. Une fonction qui satisfait cette propriété est appelée fonction quasi convexe et peut ne pas être une fonction convexe.${\style d'affichage f,}$ ${\displaystyle \{x:f(x)<a\}}$${\displaystyle \{x:f(x)\leq a\}}$${\displaystyle a\in \mathbb {R} }$
• Par conséquent, l'ensemble des minimiseurs globaux d'une fonction convexe est un ensemble convexe : - convexe.${\style d'affichage f}$${\displaystyle {\operatorname {argmin} }\,f}$
• Tout minimum local d'une fonction convexe est aussi un minimum global . Une fonction strictement convexe aura au plus un minimum global.
• L'inégalité de Jensen s'applique à toute fonction convexe . Si est une variable aléatoire prenant des valeurs dans le domaine de alors où E désigne l' espérance mathématique . En effet, les fonctions convexes sont exactement celles qui satisfont l'hypothèse de l'inégalité de Jensen .${\style d'affichage f}$${\style d'affichage X}$${\style d'affichage f,}$${\displaystyle \operatorname {E} (f(X))\geq f(\operatorname {E} (X)),}$
• Une fonction homogène du premier ordre de deux variables positives et (c'est-à-dire une fonction satisfaisant pour tout réel positif ) qui est convexe dans une variable doit être convexe dans l'autre variable.${\style d'affichage x}$${\style d'affichage y,}$${\style d'affichage f(ax,ay)=af(x,y)}$${\style d'affichage a,x,y>0}$

Opérations qui préservent la convexité

• ${\style d'affichage -f}$est concave si et seulement si est convexe.${\style d'affichage f}$
• Sommes pondérées non négatives :
  • si et sont tous convexes, alors . En particulier, la somme de deux fonctions convexes est convexe.${\displaystyle w_{1},\ldots ,w_{n}\geq 0}$${\displaystyle f_{1},\ldots ,f_{n}}$${\displaystyle w_{1}f_{1}+\cdots +w_{n}f_{n}}$
  • cette propriété s'étend également aux sommes infinies, aux intégrales et aux valeurs attendues (à condition qu'elles existent).
• Maximum par élément : soit une collection de fonctions convexes. Alors est convexe. Le domaine de est l'ensemble des points où l'expression est finie. Cas particuliers importants : ${\displaystyle \{f_{i}\}_{i\in I}}$${\displaystyle g(x)=\sup _{i\in I}f_{i}(x)}$${\style d'affichage g(x)}$
  • Si sont des fonctions convexes alors il en est de même${\displaystyle f_{1},\ldots ,f_{n}}$${\displaystyle g(x)=\max\{f_{1}(x),\ldots ,f_{n}(x)\}}$
  • Théorème de Danskin : Si est convexe dans alors est convexe dans même si C n'est pas un ensemble convexe .${\style d'affichage f(x,y)}$${\style d'affichage x}$${\displaystyle g(x)=\sup \nolimits _{y\in C}f(x,y)}$${\style d'affichage x}$
• Composition:
  • Si f et g sont des fonctions convexes et que g est non décroissant sur un domaine univarié, alors est convexe. Par exemple, si est convexe, alors . car est convexe et augmente de façon monotone.${\style d'affichage h(x)=g(f(x))}$${\style d'affichage f}$${\style d'affichage e^{f(x)}}$${\style d'affichage e^{x}}$
  • Si f est concave et g est convexe et non croissant sur un domaine univarié, alors est convexe.${\style d'affichage h(x)=g(f(x))}$
  • La convexité est invariante sous les applications affines : c'est-à-dire que si f est convexe avec domaine , alors , où avec domaine .${\displaystyle D_{f}\subseteq \mathbf {R} ^{m}}$${\style d'affichage g(x)=f(Ax+b)}$${\displaystyle A\in \mathbf {R} ^{m\times n}{\text{, }}b\in \mathbf {R} ^{m}}$${\displaystyle D_{g}\subseteq \mathbf {R} ^{n}}$
• Minimisation : Si est convexe en alors est convexe en x , à condition que C soit un ensemble convexe et que${\style d'affichage f(x,y)}$${\style d'affichage (x,y)}$${\displaystyle g(x)=\inf \nolimits _{y\in C}f(x,y)}$${\displaystyle g(x)\neq -\infty }$
• Si est convexe, alors sa perspective avec domaine est convexe.${\style d'affichage f}$${\displaystyle g(x,t)=tf\left({\tfrac {x}{t}}\right)}$${\displaystyle \left\lbrace (x,t)\mid {\tfrac {x}{t}}\in \operatorname {Dom} (f),t>0\right\rbrace }$

Fonctions fortement convexes

Le concept de convexité forte étend et paramétrise la notion de convexité stricte. Une fonction fortement convexe est également strictement convexe, mais pas l'inverse.

Une fonction dérivable est dite fortement convexe de paramètre m > 0 si l'inégalité suivante est vérifiée pour tous les points x , y de son domaine : ${\style d'affichage f}$

$${\displaystyle (\nabla f(x)-\nabla f(y))^{T}(xy)\geq m\|xy\|_{2}^{2}}$$

$${\displaystyle \langle \nabla f(x)-\nabla f(y),xy\rangle \geq m\|xy\|^{2}}$$

. ${\style d'affichage \|\cdot \|}$

Une condition équivalente est la suivante :

$${\displaystyle f(y)\geq f(x)+\nabla f(x)^{T}(yx)+{\frac {m}{2}}\|yx\|_{2}^{2 }}$$

Il n'est pas nécessaire qu'une fonction soit dérivable pour être fortement convexe. Une troisième définition d'une fonction fortement convexe, de paramètre m , est que, pour tout x , y dans le domaine et${\style d'affichage t\dans [0,1],}$

$${\displaystyle f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)-{\frac {1}{2}}mt(1-t)\|xy\ |_{2}^{2}}$$

Notez que cette définition se rapproche de la définition de la convexité stricte comme m → 0, et est identique à la définition d'une fonction convexe lorsque m = 0. Malgré cela, il existe des fonctions qui sont strictement convexes mais ne sont pas fortement convexes pour tout m > 0 ( voir exemple ci-dessous).

Si la fonction est deux fois continûment dérivable, alors elle est fortement convexe de paramètre

= 0, cela signifie que la Hessienne est semi-définie positive (ou si le domaine est la ligne réelle, cela signifie que ), ce qui implique que la fonction est convexe, et peut-être strictement convexe, mais pas fortement convexe. ${\style d'affichage f}$${\displaystyle \nabla ^{2}f(x)\succeq mI}$${\displaystyle \nabla ^{2}f}$${\style d'affichage \succeq }$${\displaystyle \nabla ^{2}f(x)-mI}$${\displaystyle \nabla ^{2}f(x)}$${\displaystyle \nabla ^{2}f(x)}$${\style d'affichage f''(x),}$${\style d'affichage f''(x)\geq m}$${\displaystyle f''(x)\geq 0}$

En supposant toujours que la fonction est deux fois continûment dérivable, on peut montrer que la borne inférieure de implique qu'elle est fortement convexe. En utilisant

il existe ${\displaystyle \nabla ^{2}f(x)}$

$${\displaystyle z\in \{tx+(1-t)y:t\in [0,1]\}}$$

tel que

$${\displaystyle f(y)=f(x)+\nabla f(x)^{T}(yx)+{\frac {1}{2}}(yx)^{T}\nabla ^{2} f(z)(yx)}$$

Puis

$${\displaystyle (yx)^{T}\nabla ^{2}f(z)(yx)\geq m(yx)^{T}(yx)}$$

par l'hypothèse sur les valeurs propres, et donc on retrouve la deuxième équation de convexité forte ci-dessus.

Une fonction est fortement convexe de paramètre

si et seulement si la fonction ${\style d'affichage f}$

$${\displaystyle x\mapsto f(x)-{\frac {m}{2}}\|x\|^{2}}$$

est convexe.

La distinction entre convexe, strictement convexe et fortement convexe peut être subtile à première vue. Si est deux fois continûment dérivable et le domaine est la droite réelle, alors nous pouvons le caractériser comme suit : ${\style d'affichage f}$

• ${\style d'affichage f}$convexe si et seulement si pour tout

.${\displaystyle f''(x)\geq 0}$

${\style d'affichage f}$strictement convexe si pour tout

(note : c'est suffisant, mais pas nécessaire).${\style d'affichage f''(x)>0}$

${\style d'affichage f}$fortement convexe si et seulement si pour tout

.${\displaystyle f''(x)\geq m>0}$

Par exemple, soit strictement convexe, et supposons qu'il existe une suite de points telle que . Même si , la fonction n'est pas fortement convexe car deviendra arbitrairement petite. ${\style d'affichage f}$${\style d'affichage (x_{n})}$${\displaystyle f''(x_{n})={\tfrac {1}{n}}}$${\style d'affichage f''(x_{n})>0}$${\style d'affichage f''(x)}$

Une fonction deux fois continûment dérivable sur un domaine compact qui satisfait pour tout est fortement convexe. La preuve de cet énoncé découle du

, qui stipule qu'une fonction continue sur un ensemble compact a un maximum et un minimum. ${\style d'affichage f}$${\style d'affichage X}$${\style d'affichage f''(x)>0}$${\style d'affichage x\dans X}$

Les fonctions fortement convexes sont en général plus faciles à utiliser que les fonctions convexes ou strictement convexes, car elles constituent une classe plus petite. Comme les fonctions strictement convexes, les fonctions fortement convexes ont des minima uniques sur des ensembles compacts.

Fonctions uniformément convexes

Une fonction uniformément convexe, de module , est une fonction qui, pour tout

, satisfait ${\style d'affichage \phi }$${\style d'affichage f}$

$${\style d'affichage f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)-t(1-t)\phi (\|xy\|)}$$

où est une fonction qui est non négative et ne s'annule qu'en 0. Ceci est une généralisation du concept de fonction fortement convexe ; en prenant on retrouve la définition de forte convexité. ${\style d'affichage \phi }$${\displaystyle \phi (\alpha )={\tfrac {m}{2}}\alpha ^{2}}$

Exemples

Fonctions d'une variable

• La fonction a , donc

est une fonction convexe. Il est également fortement convexe (et donc strictement convexe aussi), avec une forte convexité constante 2.${\style d'affichage f(x)=x^{2}}$${\style d'affichage f''(x)=2>0}$

La fonction a , donc

est une fonction convexe. Elle est strictement convexe, même si la dérivée seconde n'est pas strictement positive en tous points. Il n'est pas fortement convexe.${\style d'affichage f(x)=x^{4}}$${\displaystyle f''(x)=12x^{2}\geq 0}$

La fonction valeur absolue est convexe (comme reflété dans l'

 = 0. Elle n'est pas strictement convexe.${\style d'affichage f(x)=|x|}$

La fonction pour est convexe.${\style d'affichage f(x)=|x|^{p}}$${\style d'affichage p\geq 1}$

La fonction exponentielle est convexe. Elle est aussi strictement convexe, puisque , mais elle n'est pas fortement convexe puisque la dérivée seconde peut être arbitrairement proche de zéro. Plus généralement, la fonction est

est une fonction convexe. Le terme "superconvexe" est parfois utilisé à la place.${\style d'affichage f(x)=e^{x}}$${\displaystyle f''(x)=e^{x}>0}$${\style d'affichage g(x)=e^{f(x)}}$

La fonction de domaine [0,1] définie par for est convexe ; elle est continue sur l'intervalle ouvert (0, 1), mais pas continue à 0 et 1.${\style d'affichage f}$${\style d'affichage f(0)=f(1)=1,f(x)=0}$${\style d'affichage 0<x<1}$

La fonction x ³ a une dérivée seconde 6 x ; il est donc convexe sur l'ensemble où x 0 et concave sur l'ensemble où  x  ≤ 0.

Des exemples de fonctions qui augmentent de manière monotone mais non convexes incluent et .${\displaystyle f(x)={\sqrt {x}}}$${\displaystyle g(x)=\log x}$

Des exemples de fonctions convexes mais non croissantes de manière monotone incluent et .${\style d'affichage h(x)=x^{2}}$${\style d'affichage k(x)=-x}$

La fonction a qui est supérieure à 0 si

> 0, est donc convexe sur l'intervalle . Il est concave sur l'intervalle .${\displaystyle f(x)={\tfrac {1}{x}}}$${\displaystyle f''(x)={\tfrac {2}{x^{3}}}}$${\style d'affichage f(x)}$${\style d'affichage (0,\infty )}$${\style d'affichage (-\infty ,0)}$

La fonction avec , est convexe sur l'intervalle et convexe sur l'intervalle , mais pas convexe sur l'intervalle , à cause de la singularité à 

 = 0.${\displaystyle f(x)={\tfrac {1}{x^{2}}}}$${\style d'affichage f(0)=\infty }$${\style d'affichage (0,\infty )}$${\style d'affichage (-\infty ,0)}$${\style d'affichage (-\infty ,\infty )}$

Fonctions de n variables

• La fonction

est convexe.${\displaystyle -\log \det(X)}$

Chaque transformation linéaire à valeur réelle est convexe mais pas strictement convexe, car si f est linéaire, alors . Cette affirmation est également valable si nous remplaçons « convexe » par « concave ».${\style d'affichage f(a+b)=f(a)+f(b)}$

Toute fonction affine à valeur

, c'est-à-dire chaque fonction de la forme , est à la fois convexe et concave.${\style d'affichage f(x)=a^{T}x+b}$

Toute norme est une fonction convexe, par l' inégalité triangulaire et l' homogénéité positive .

Le rayon spectral d'une matrice non négative est une fonction convexe de ses éléments diagonaux.

Voir également

• Fonction concave
• Analyse convexe
• Conjugué convexe
• Optimisation convexe
• Convexité géodésique
• Inégalité Hermite-Hadamard
• Fonction Invex
• L'inégalité de Jensen
• Fonction K-convexe
• Le théorème de Kachurovskii , qui relie la convexité à la monotonie de la dérivée
• L'inégalité de Karamata
• Fonction logarithmiquement convexe
• Fonction pseudoconvexe
• Fonction quasi-convexe
• Dérivée d'une fonction convexe

Remarques

Les références

• Bertsekas, Dimitri (2003). Analyse convexe et optimisation . Athéna Scientifique.
• Borwein, Jonathan et Lewis, Adrian. (2000). Analyse convexe et optimisation non linéaire. Springer.
• Donoghue, William F. (1969). Distributions et transformées de Fourier . Presse académique.
• Hiriart-Urruty, Jean-Baptiste, et Lemaréchal, Claude . (2004). Fondamentaux de l'analyse convexe. Berlin : Springer.
• Krasnosel'skii MA , Rutickii Ya.B. (1961). Fonctions convexes et espaces Orlicz . Groningue : P.Noordhoff Ltd.
• Lauritzen, Niels (2013). Convexité de premier cycle . Éditions scientifiques mondiales.
• Luenberger, David (1984). Programmation linéaire et non linéaire . Addison-Wesley.
• Luenberger, David (1969). Optimisation par les méthodes de l'espace vectoriel . Wiley & Fils.
• Rockafellar, RT (1970). Analyse convexe . Princeton : Princeton University Press.
• Thomson, Brian (1994). Propriétés symétriques des fonctions réelles . Presse CRC.
• Zălinescu, C. (2002). Analyse convexe dans les espaces vectoriels généraux . River Edge, NJ : World Scientific Publishing Co., Inc. pp. xx+367. ISBN 981-238-067-1. MR  1921556 .

Liens externes

• "Fonction convexe (d'une variable réelle)" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• "Fonction convexe (d'une variable complexe)" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]