Enveloppe (mathématiques) - Envelope (mathematics)

En géométrie , une enveloppe d'une famille plane de courbes est une courbe qui est tangente à chaque membre de la famille en un point, et ces points de tangence forment ensemble l'enveloppe entière. Classiquement, un point sur l'enveloppe peut être considéré comme l'intersection de deux courbes « infiniment adjacentes », c'est-à-dire la limite des intersections de courbes voisines. Cette idée peut être généralisée à une enveloppe de surfaces dans l'espace, et ainsi de suite à des dimensions supérieures.

Pour avoir une enveloppe, il est nécessaire que les membres individuels de la famille de courbes soient des courbes différentiables car le concept de tangence ne s'applique pas autrement, et il doit y avoir une transition en douceur à travers les membres. Mais ces conditions ne sont pas suffisantes – une famille donnée peut ne pas avoir d'enveloppe. Un exemple simple de ceci est donné par une famille de cercles concentriques de rayon en expansion.

Enveloppe d'une famille de courbes

Soit chaque courbe C _t de la famille donnée comme la solution d'une équation f _t ( x ,  y )=0 (voir courbe implicite ), où t est un paramètre. Écrivez F ( t ,  x ,  y )= f _t ( x ,  y ) et supposons que F est dérivable.

L'enveloppe de la famille C _t est alors définie comme l'ensemble des points ( x , y ) pour lesquels, simultanément, ${\displaystyle {\mathcal {D}}}$

${\displaystyle F(t,x,y)=0~~{\mathsf {et}}~~{\partial F \over \partial t}(t,x,y)=0}$

pour une certaine valeur de t , où est la dérivée partielle de F par rapport à t . ${\displaystyle \partial F/\partial t}$

Si t et u , t ≠ u sont deux valeurs du paramètre , puis l'intersection de la courbe C _t et C _u est donnée par

${\style d'affichage F(t,x,y)=F(u,x,y)=0\,}$

ou équivalent,

${\displaystyle F(t,x,y)=0~~{\mathsf {et}}~~{\frac {F(u,x,y)-F(t,x,y)}{ut}} =0.}$

Laisser u → t donne la définition ci-dessus.

Un cas particulier important est lorsque F ( t ,  x ,  y ) est un polynôme en t . Cela inclut, en éliminant les dénominateurs , le cas où F ( t ,  x ,  y ) est une fonction rationnelle dans t . Dans ce cas, la définition revient à t étant une racine double de F ( t ,  x ,  y ), donc l'équation de l'enveloppe peut être trouvée en mettant le discriminant de F à 0 (car la définition demande F=0 à un certain t et dérivée première =0 c'est-à-dire sa valeur 0 et c'est min/max à ce t).

Par exemple, soit C _t la ligne dont les interceptions x et y sont t et 11− t , ceci est montré dans l'animation ci-dessus. L'équation de C _t est

${\displaystyle {\frac {x}{t}}+{\frac {y}{11-t}}=1}$

ou, effacement des fractions,

${\style d'affichage x(11-t)+yt-t(11-t)=t^{2}+(-x+y-11)t+11x=0.\,}$

L'équation de l'enveloppe est alors

${\style d'affichage (-x+y-11)^{2}-44x=(xy)^{2}-22(x+y)+121=0.\,}$

Souvent, lorsque F n'est pas une fonction rationnelle du paramètre, il peut être réduit à ce cas par une substitution appropriée. Par exemple, si la famille est donnée par C _θ avec une équation de la forme u ( x ,  y )cos θ+ v ( x ,  y )sin θ= w ( x ,  y ), alors en mettant t = e ^{i θ} , cos θ=( t +1/ t )/2, sin =( t -1/ t )/2 i change l'équation de la courbe en

${\displaystyle u{1 \over 2}(t+{1 \over t})+v{1 \over 2i}(t-{1 \over t})=w}$

ou alors

${\style d'affichage (u-iv)t^{2}-2wt+(u+iv)=0.\,}$

L'équation de l'enveloppe est alors donnée en mettant le discriminant à 0 :

${\style d'affichage (u-iv)(u+iv)-w^{2}=0\,}$

ou alors

${\displaystyle u^{2}+v^{2}=w^{2}.\,}$

Définitions alternatives

1. L'enveloppe E ₁ est la limite des intersections des courbes voisines C _t .
2. L'enveloppe E ₂ est une courbe tangente à l'ensemble des C _t .
3. L'enveloppe E ₃ est la limite de la région remplie par les courbes C _t .

Alors , et , où est l'ensemble de points défini au début de la section parent de cette sous-section. ${\displaystyle E_{1}\subseteq {\mathcal {D}}}$${\displaystyle E_{2}\subseteq {\mathcal {D}}}$${\displaystyle E_{3}\subseteq {\mathcal {D}}}$${\displaystyle {\mathcal {D}}}$

Exemples

Exemple 1

Ces définitions E ₁ , E ₂ et E ₃ de l'enveloppe peuvent être des ensembles différents. Considérons par exemple la courbe y = x ³ paramétrée par γ : R → R ² où γ( t ) = ( t , t ³ ) . La famille de courbes à un paramètre sera donnée par les droites tangentes à .

On calcule d'abord le discriminant . La fonction génératrice est ${\displaystyle {\mathcal {D}}}$

${\style d'affichage F(t,(x,y))=3t^{2}xy-2t^{3}.}$

Calcul de la dérivée partielle F _t = 6 t ( x – t ) . Il s'ensuit que soit x = t soit t = 0 . Supposons d'abord que x = t et t 0 . Substituant dans F : et donc, en supposant que t 0, il s'ensuit que F = F _t = 0 si et seulement si ( x , y ) = ( t , t ³ ) . Ensuite, en supposant que t = 0 et en le substituant dans F donne F (0,( x , y )) = − y . Donc, en supposant t = 0 , il s'ensuit que F = F _t = 0 si et seulement si y = 0 . Ainsi le discriminant est la courbe d'origine et sa tangente à (0) : ${\style d'affichage F(t,(t,y))=t^{3}-y\,}$

${\displaystyle {\mathcal {D}}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\cup \{(x,y)\in \mathbb {R} ^{2}:y=0\}\ .}$

Ensuite, nous calculons E ₁ . Une courbe est donnée par F ( t ,( x , y )) = 0 et une courbe voisine est donnée par F ( t + ,( x , y )) où est un très petit nombre. Le point d'intersection vient de la limite de F ( t ,( x , y )) =  F ( t + ,( x , y )) lorsque ε tend vers zéro. Notez que F ( t ,( x , y )) =  F ( t + ε,( x , y )) si et seulement si

${\displaystyle L:=F(t,(x,y))-F(t+\varepsilon ,(x,y))=2\varepsilon ^{3}+6\varepsilon t^{2}+6\varepsilon ^{2}t-(3\varepsilon ^{2}+6\varepsilon t)x=0.}$

Si t 0 alors L n'a qu'un seul facteur de ε. En supposant que t 0 alors l'intersection est donnée par

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon }}L=6t(tx)\ .}$

Puisque t 0, il s'ensuit que x = t . La valeur y est calculée en sachant que ce point doit se trouver sur une ligne tangente à la courbe d'origine γ : que F ( t ,( x , y )) = 0 . Substituer et résoudre donne y = t ³ . Lorsque t = 0 , L est divisible par ² . En supposant que t = 0 alors l'intersection est donnée par

${\displaystyle \lim _{\varepsilon \to 0}{\frac {1}{\varepsilon ^{2}}}L=3x\ .}$

Il s'ensuit que x = 0 , et sachant que F ( t ,( x , y )) = 0 donne y = 0 . Il s'ensuit que

${\displaystyle E_{1}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

Ensuite, nous calculons E ₂ . La courbe elle-même est la courbe qui est tangente à toutes ses propres lignes tangentes. Il s'ensuit que

${\displaystyle E_{2}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .}$

Enfin on calcule E ₃ . Chaque point du plan a au moins une ligne tangente à γ qui le traverse, et donc la région remplie par les lignes tangentes est le plan entier. La frontière E ₃ est donc l'ensemble vide. En effet, considérons un point dans le plan, disons ( x ₀ , y ₀ ). Ce point est sur une tangente si et seulement s'il existe un t tel que

${\displaystyle F(t,(x_{0},y_{0}))=3t^{2}x_{0}-y_{0}-2t^{3}=0\ .}$

C'est une cubique en t et en tant que telle a au moins une solution réelle. Il s'ensuit qu'au moins une ligne tangente à doit passer par un point donné du plan. Si y > x ³ et y > 0 alors chaque point ( x , y ) a exactement une tangente à qui le traverse. Il en est de même si y < x ³ y < 0 . Si y < x ³ et y > 0 alors chaque point ( x , y ) a exactement trois lignes tangentes distinctes à qui le traverse. Il en est de même si y > x ³ et y < 0 . Si y = x ³ et y 0 alors chaque point ( x , y ) a exactement deux droites tangentes à qui le traverse (cela correspond à la cubique ayant une racine ordinaire et une racine répétée). Il en est de même si y ≠ x ³ et y = 0 . Si y = x ³ et x = 0 , c'est-à-dire x = y = 0 , alors ce point est traversé par une seule tangente à γ (cela correspond à la cubique ayant une racine réelle de multiplicité 3). Il s'ensuit que

${\displaystyle E_{3}=\varnothing .}$

Exemple 2

Dans l' art des cordes, il est courant de croiser deux lignes de broches équidistantes. Quelle courbe se forme ?

Pour plus de simplicité, placez les broches sur les axes x et y ; une disposition non orthogonale est une rotation et une mise à l' échelle . Un fil de droite général relie les deux points (0, k − t ) et ( t , 0 ), où k est une constante d'échelle arbitraire, et la famille de lignes est générée en faisant varier le paramètre t . De géométrie simple, l'équation de cette droite est y = −( k  −  t ) x / t + k  −  t . Le réarrangement et le transtypage sous la forme F ( x , y , t ) = 0 donne :

${\style d'affichage F(x,y,t)=-{\frac {kx}{t}}-t+x+ky=0\,}$

(1)

Dérivez maintenant F ( x , y , t ) par rapport à t et définissez le résultat égal à zéro, pour obtenir

${\displaystyle {\frac {\partial F(x,y,t)}{\partial t}}={\frac {kx}{t^{2}}}-1=0\,}$

(2)

Ces deux équations définissent conjointement l'équation de l'enveloppe. De (2) on a :

${\displaystyle t={\sqrt {kx}}\,}$

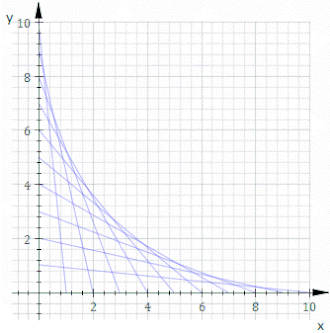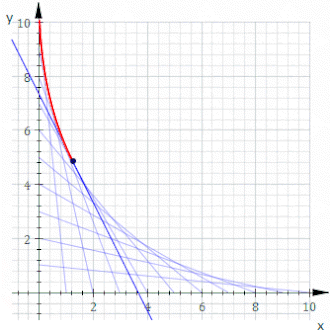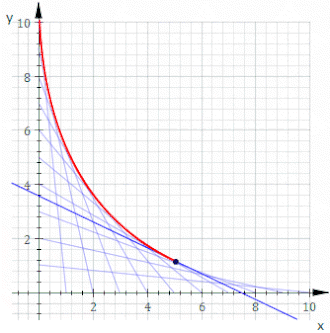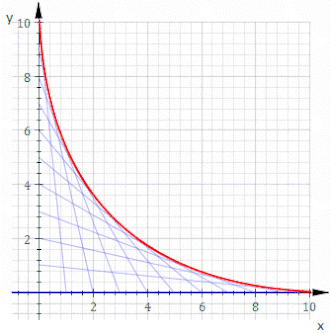
En substituant cette valeur de t à (1) et en simplifiant, on obtient une équation pour l'enveloppe :

${\displaystyle y=({\sqrt {x}}-{\sqrt {k}})^{2}\,}$

(3)

Ou, en réorganisant sous une forme plus élégante qui montre la symétrie entre x et y :

${\displaystyle {\sqrt {x}}+{\sqrt {y}}={\sqrt {k}}}$

(4)

On peut prendre une rotation des axes où le b axe est la ligne y = x orienté nord -est et l' un axe est la ligne y = -x sud orienté. Ces nouveaux axes sont liés aux originaux xy axes par x = (b + a) / √ 2 et y = (ba) / √ 2 . On obtient, après substitution en (4) et développement et simplification,

${\displaystyle b={\frac {1}{k{\sqrt {2}}}}a^{2}+{\frac {k}{2{\sqrt {2}}}}}$,

(5)

qui est apparemment l'équation d'une parabole d'axe suivant a=0 , ou y=x .

Exemple 3

Soit I ⊂ R un intervalle ouvert et soit γ : I → R ² une courbe plane lisse paramétrée par la longueur de l'arc . Considérons la famille à un paramètre de droites normales à γ( I ). Une droite est normale à en ( t ) si elle passe par γ( t ) et est perpendiculaire au vecteur tangent à en ( t ). Soit T le vecteur tangent unitaire à et N le vecteur normal unitaire . En utilisant un point pour désigner le produit scalaire , la famille génératrice de la famille à un paramètre de droites normales est donnée par F  : I × R ² → R où

${\displaystyle F(t,{\mathbf {x} })=({\mathbf {x} }-\gamma (t))\cdot {\mathbf {T} }(t)\ .}$

Clairement ( x − γ)· T = 0 si et seulement si x − γ est perpendiculaire à T , ou de façon équivalente, si et seulement si x − est parallèle à N , ou de façon équivalente, si et seulement si x = γ + λ N pour certains λ ∈ R . Il s'ensuit que

${\displaystyle L_{t_{0}}:=\{{\mathbf {x} }\in \mathbb {R} ^{2}:F(t_{0},{\mathbf {x} })=0 \}}$

est exactement la droite normale à en ( t ₀ ). Pour trouver le discriminant de F nous devons calculer sa dérivée partielle par rapport à t :

${\displaystyle {\frac {\partial F}{\partial t}}(t,{\mathbf {x} })=\kappa (t)({\mathbf {x} }-\gamma (t))\ cdot {\mathbf {N} }(t)-1\ ,}$

où est la courbure de la courbe plane de γ. On a vu que F = 0 si et seulement si x - γ = λ N pour un certain λ ∈ R . En supposant que F = 0 donne

${\displaystyle {\frac {\partial F}{\partial t}}=\lambda \kappa (t)-1\ .}$

En supposant que κ ≠ 0 il s'ensuit que λ = 1/κ et donc

${\displaystyle {\mathcal {D}}=\gamma (t)+{\frac {1}{\kappa (t)}}{\mathbf {N} }(t)\ .}$

C'est exactement la développée de la courbe .

Exemple 4

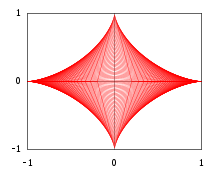
L'exemple suivant montre que dans certains cas l'enveloppe d'une famille de courbes peut être vue comme la frontière topologique d'une union d'ensembles, dont les frontières sont les courbes de l'enveloppe. Pour et considérer le triangle rectangle (ouvert) dans un plan cartésien de sommets , et${\style d'affichage s>0}$${\style d'affichage t>0}$${\style d'affichage (0,0)}$${\style d'affichage (s,0)}$${\style d'affichage (0,t)}$

${\displaystyle T_{s,t}:=\left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\ frac {y}{t}}<1\right\}.}$

Fixer un exposant et considérer l'union de tous les triangles soumis à la contrainte , c'est-à-dire l'ouvert ${\displaystyle \alpha >0}$${\style d'affichage T_{s,t}}$${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$

${\displaystyle \Delta _{\alpha }:=\bigcup _{s^{\alpha }+t^{\alpha }=1}T_{s,t}.}$

Pour écrire une représentation cartésienne pour , commencez par any , satisfaisant et any . L' inégalité de Hölder en ce qui concerne les exposants conjugués et donne: ${\displaystyle \textstyle \Delta _{\alpha }}$${\displaystyle \textstyle s>0}$${\displaystyle \textstyle t>0}$${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$${\displaystyle \textstyle (x,y)\in \mathbb {R} _{+}^{2}}$${\displaystyle \textstyle \mathbb {R} ^{2}}$${\displaystyle p:=1+{\frac {1}{\alpha }}}$${\displaystyle \textstyle q:={1+\alpha }}$

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}\leq \left({\frac {x}{s} }+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}{\Big (}s^{\alpha }+t^{\alpha }{\ Grand )}^{\frac {1}{\alpha +1}}=\left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac { \alpha }{\alpha +1}}}$,

avec égalité si et seulement si . En termes d'union d'ensembles, la dernière inégalité s'écrit : le point appartient à l'ensemble , c'est-à-dire qu'il appartient à certains avec , si et seulement s'il satisfait ${\displaystyle \textstyle s:\,t=x^{\frac {1}{1+\alpha }}:\,y^{\frac {1}{1+\alpha }}}$${\displaystyle (x,y)\in \mathbb {R} _{+}^{2}}$${\displaystyle \textstyle \Delta _{\alpha }}$${\displaystyle \textstyle T_{s,t}}$${\displaystyle \textstyle s^{\alpha }+t^{\alpha }=1}$

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}<1.}$

De plus, la frontière de l'ensemble est l'enveloppe de la famille correspondante de segments de droite ${\displaystyle \mathbb {R} _{+}^{2}}$${\displaystyle \textstyle \Delta _{\alpha }}$

${\displaystyle \left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}} =1\right\}\ ,\qquad s^{\alpha }+t^{\alpha }=1}$

(c'est-à-dire les hypoténuses des triangles), et a l'équation cartésienne

${\displaystyle x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}=1.}$

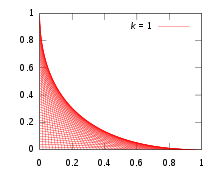
Notez que, en particulier, la valeur donne l'arc de parabole de l' exemple 2 , et la valeur (ce qui signifie que toutes les hypoténuses sont des segments de longueur unitaire) donne l' astroïde . ${\style d'affichage \alpha =1}$${\style d'affichage \alpha =1}$

Exemple 5

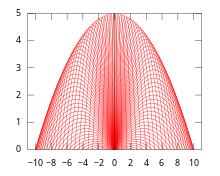
On considère l'exemple suivant d'enveloppe en mouvement. Supposons qu'à la hauteur initiale 0, on lance un projectile en l'air avec une vitesse initiale constante v mais des angles d'élévation θ différents. Soit x l'axe horizontal de la surface de mouvement, et y l'axe vertical. Alors le mouvement donne le système dynamique différentiel suivant :

${\displaystyle {\frac {d^{2}y}{dt^{2}}}=-g,\;{\frac {d^{2}x}{dt^{2}}}=0, }$

qui satisfait quatre conditions initiales :

${\displaystyle {\frac {dx}{dt}}{\bigg |}_{t=0}=v\cos \theta ,\;{\frac {dy}{dt}}{\bigg |}_{ t=0}=v\sin \theta ,\;x{\bigg |}_{t=0}=y{\bigg |}_{t=0}=0.}$

Ici, t désigne le temps de mouvement, est l'angle d'élévation, g désigne l'accélération gravitationnelle et v est la vitesse initiale constante (pas la vitesse ). La solution du système ci-dessus peut prendre une forme implicite :

${\displaystyle F(x,y,\theta )=x\tan \theta -{\frac {gx^{2}}{2v^{2}\cos ^{2}\theta }}-y=0. }$

Pour trouver son équation enveloppe, on peut calculer la dérivée souhaitée :

${\displaystyle {\frac {\partial F}{\partial \theta }}={\frac {x}{\cos ^{2}\theta }}-{\frac {gx^{2}\tan \theta }{v^{2}\cos ^{2}\theta }}=0.}$

En éliminant θ, on peut atteindre l'équation enveloppe suivante :

${\displaystyle y={\frac {v^{2}}{2g}}-{\frac {g}{2v^{2}}}x^{2}.}$

Il est clair que l'enveloppe résultante est également une parabole concave .

Enveloppe d'une famille de surfaces

Une famille de surfaces à un paramètre dans l'espace euclidien tridimensionnel est donnée par un ensemble d'équations

${\style d'affichage F(x,y,z,a)=0}$

en fonction d'un paramètre réel a . Par exemple, les plans tangents à une surface le long d'une courbe de la surface forment une telle famille.

Deux surfaces correspondant à des valeurs différentes a et a' se coupent dans une courbe commune définie par

${\displaystyle F(x,y,z,a)=0,\,\,{F(x,y,z,a^{\prime })-F(x,y,z,a) \sur un ^{\prime }-a}=0.}$

A la limite lorsque a' se rapproche de a , cette courbe tend vers une courbe contenue dans la surface en un

${\displaystyle F(x,y,z,a)=0,\,\,{\partial F \over \partial a}(x,y,z,a)=0.}$

Cette courbe est appelée la caractéristique de la famille en a . Comme a varie le lieu de ces courbes caractéristiques définit une surface appelée enveloppe de la famille des surfaces.

L'enveloppe d'une famille de surfaces est tangente à chaque surface de la famille le long de la courbe caractéristique de cette surface.

Généralisations

L'idée d'une enveloppe d'une famille de sous-variétés lisses suit naturellement. En général, si nous avons une famille de sous-variétés de codimension c alors nous devons avoir au moins une famille de paramètres c de telles sous-variétés. Par exemple : une famille de courbes à un paramètre dans trois espaces ( c = 2) n'a pas, génériquement, d'enveloppe.

Applications

Équations différentielles ordinaires

Les enveloppes sont liées à l'étude des équations différentielles ordinaires (EDO), et en particulier des solutions singulières d'EDO. Considérons, par exemple, la famille à un paramètre de droites tangentes à la parabole y = x ² . Ceux-ci sont donnés par la famille génératrice F ( t ,( x , y )) = t ² – 2 tx + y . L'ensemble de niveau zéro F ( t ₀ ,( x , y )) = 0 donne l'équation de la tangente à la parabole au point ( t ₀ , t ₀ ² ). L'équation t ² – 2 tx + y = 0 peut toujours être résolue pour y en fonction de x et donc, considérons

${\style d'affichage t^{2}-2tx+y(x)=0.\ }$

Substitution

${\displaystyle t=\left({\frac {dy}{dx}}\right)/2}$

donne l'ODE

${\displaystyle \left({\frac {dy}{dx}}\right)^{2}\!\!-4x{\frac {dy}{dx}}+4y=0.}$

Sans surprise, y  = 2 tx  −  t ² sont toutes des solutions à cette ODE. Cependant, l'enveloppe de cette famille de droites à un paramètre, qui est la parabole y  =  x ² , est aussi une solution à cette ODE. Un autre exemple célèbre est l'équation de Clairaut .

Équations aux dérivées partielles

Les enveloppes peuvent être utilisées pour construire des solutions plus compliquées d' équations aux dérivées partielles (EDP) du premier ordre à partir d'équations plus simples. Soit F ( x , u ,D u ) = 0 une EDP du premier ordre, où x est une variable avec des valeurs dans un ouvert Ω ⊂  R ⁿ , u est une fonction à valeur réelle inconnue, D u est le gradient de u , et F est une fonction continûment dérivable et régulière dans D u . Supposons que u ( x , a ) est un m -parameter famille de solutions: qui est, pour chaque fixe un  ∈  A  ⊂  R ^m , u ( x , a ) est une solution de l'équation différentielle. Une nouvelle solution de l'équation différentielle peut être construite en résolvant d'abord (si possible)

${\displaystyle D_{a}u(x;a)=0\,}$

pour a  = ( x ) en fonction de x . L'enveloppe de la famille de fonctions { u (·, a )} _{a ∈ A} est définie par

${\displaystyle v(x)=u(x;\varphi (x)),\quad x\in \Omega ,}$

et résout également l'équation différentielle (à condition qu'elle existe en tant que fonction continuellement différentiable).

Géométriquement, le graphe de v ( x ) est partout tangent au graphe d'un membre de la famille u ( x ; a ). Puisque l'équation différentielle est du premier ordre, elle ne pose qu'une condition sur le plan tangent au graphique, de sorte que toute fonction tangente partout à une solution doit également être une solution. La même idée sous-tend la résolution d'une équation du premier ordre en tant qu'intégrale du cône de Monge . Le cône de Monge est un champ de cône dans le R ^{n +1} des variables ( x , u ) découpé par l'enveloppe des espaces tangents à l'EDP du premier ordre en chaque point. Une solution de l'EDP est alors une enveloppe du champ de cône.

En géométrie riemannienne , si une famille lisse de géodésiques passant par un point P dans une variété riemannienne a une enveloppe, alors P a un point conjugué où toute géodésique de la famille coupe l'enveloppe. Il en est de même plus généralement dans le calcul des variations : si une famille d'extrémales à une fonctionnelle passant par un point donné P a une enveloppe, alors un point où un extrémal coupe l'enveloppe est un point conjugué à P .

caustiques

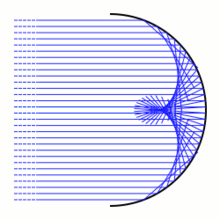
En optique géométrique , une caustique est l'enveloppe d'une famille de rayons lumineux . Dans cette image, il y a un arc de cercle. Les rayons lumineux (en bleu) proviennent d'une source à l'infini et arrivent donc parallèlement. Lorsqu'ils frappent l'arc de cercle, les rayons lumineux sont diffusés dans différentes directions selon la loi de la réflexion . Lorsqu'un rayon lumineux frappe l'arc en un point, la lumière sera réfléchie comme si elle avait été réfléchie par la ligne tangente de l'arc en ce point. Les rayons lumineux réfléchis donnent une famille de lignes à un paramètre dans le plan. L'enveloppe de ces lignes est la caustique réfléchissante . Une caustique réfléchissante sera constituée de manière générique de points lisses et de points de rebroussement ordinaires .

Du point de vue du calcul des variations, le principe de Fermat (sous sa forme moderne) implique que les rayons lumineux sont les extrémaux pour la longueur fonctionnelle

${\displaystyle L[\gamma ]=\int _{a}^{b}|\gamma '(t)|\,dt}$

parmi des courbes lisses γ sur [ a , b ] avec des extrémités fixes γ( a ) et γ( b ). La caustique déterminée par un point donné P (dans l'image le point est à l'infini) est l'ensemble des points conjugués à P .

Le principe de Huygens

La lumière peut traverser des milieux inhomogènes anisotropes à des vitesses différentes selon la direction et la position de départ d'un rayon lumineux. La frontière de l'ensemble des points vers lesquels la lumière peut voyager à partir d'un point donné q après un temps t est connue sous le nom de front d'onde après le temps t , noté ici Φ _q ( t ). Il se compose précisément des points qui peuvent être atteints à partir de q au temps t en voyageant à la vitesse de la lumière. Le principe de Huygens affirme que l'ensemble des fronts d'onde Φ _{q 0} ( s + t ) est l'enveloppe de la famille des fronts d'onde Φ _q ( s ) pour q  Φ _{q 0} ( t ). Plus généralement, le point q ₀ pourrait être remplacé par n'importe quelle courbe, surface ou ensemble fermé dans l'espace.

Voir également

• Surface réglée
• Caustique (mathématiques)

Les références

Liens externes

• Weisstein, Eric W. "Enveloppe" . MathWorld .
• "Enveloppe d'une famille de courbes planes" chez MathCurve.