G ₂ (mathématiques) -G₂ (mathematics)

Structure algébrique → Théorie des groupes Théorie des groupes
Notions de base Sous-groupe Sous-groupe normal Groupe quotient Produit (semi-) direct Homomorphismes de groupe noyau image somme directe produit de couronne Facile fini infini continu multiplicatif additif cyclique abélien dièdre nilpotent soluble action Glossaire de la théorie des groupes Liste des sujets de théorie des groupes
Groupes finis Classification des groupes simples finis cyclique en alternance Type de mensonge sporadique Le théorème de Cauchy Le théorème de Lagrange Théorèmes de Sylow théorème de Hall groupe p Groupe abélien élémentaire Groupe Frobenius Multiplicateur de Schur Groupe symétrique S n Klein quatre groupe V Groupe dièdre D n Groupe de quaternions Q Groupe dicyclique Dic n
Groupes discrets Treillis Entiers ( )${\displaystyle \mathbb {Z} }$ Groupe gratuit Groupes modulaires PSL(2, )${\displaystyle \mathbb {Z} }$ SL(2, )${\displaystyle \mathbb {Z} }$ Groupe arithmétique Treillis Groupe hyperbolique
Groupes topologiques et de Lie Solénoïde Cercle GL linéaire général ( n ) Linéaire spécial SL( n ) O orthogonal ( n ) Euclidien E( n ) Spécial orthogonal SO( n ) Unitaire U( n ) Unité spéciale SU( n ) Sp symplectique ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Conforme Difféomorphisme Boucle Groupe de Lie de dimension infinie O(∞) SU(∞) Sp(∞)
Groupes algébriques Groupe algébrique linéaire Groupe réducteur Variété abélienne Courbe elliptique
v t e

Groupes de mensonges
Groupes classiques
Groupes de mensonges simples Classique Un n B n C n D n Exceptionnel G 2 F 4 E 6 E 7 E 8
Autres groupes de Mensonges Cercle Lorentz Poincaré Groupe conforme Difféomorphisme Boucle euclidien
Algèbres de Lie
Algèbre de Lie semi-simple
Théorie des représentations
Les groupes de mensonges en physique
Scientifiques Sophus Mensonge Henri Poincaré Wilhelm tuant Élie Cartan Hermann Weyl Claude Chevalley Harish-Chandra Armand Borel
Glossaire Tableau des groupes de Lie
v t e

En mathématiques , G ₂ est le nom de trois groupes de Lie simples (une forme complexe, une forme réelle compacte et une forme réelle divisée), leurs algèbres de Lie ainsi que certains groupes algébriques . Ils sont le plus petit des cinq groupes de Lie simples exceptionnels . G ₂ a le rang 2 et la dimension 14. Il a deux représentations fondamentales , de dimension 7 et 14. ${\displaystyle {\mathfrak {g}}_{2},}$

La forme compacte de G ₂ peut être décrite comme le groupe d'automorphisme de l' algèbre d'octonions ou, de manière équivalente, comme le sous-groupe de SO (7) qui préserve tout vecteur particulier choisi dans sa représentation de spineur réel à 8 dimensions (une représentation de spin ).

Histoire

L'algèbre de Lie , étant la plus petite algèbre de Lie simple exceptionnelle, a été la première d'entre elles à être découverte dans la tentative de classification des algèbres de Lie simples. Le 23 mai 1887, Wilhelm Killing écrivit une lettre à Friedrich Engel disant qu'il avait trouvé une algèbre de Lie simple à 14 dimensions, que nous appelons maintenant . ${\displaystyle {\mathfrak {g}}_{2}}$${\displaystyle {\mathfrak {g}}_{2}}$

En 1893, Élie Cartan publia une note décrivant un ensemble ouvert doté d'une distribution bidimensionnelle — c'est-à-dire un champ de sous-espaces bidimensionnels variant doucement de l'espace tangent — pour lequel l'algèbre de Lie apparaît comme les symétries infinitésimales. La même année, dans le même journal, Engel remarqua la même chose. Plus tard, il a été découvert que la distribution bidimensionnelle est étroitement liée à une balle roulant sur une autre balle. L'espace des configurations de la bille roulante est en 5 dimensions, avec une distribution en 2 dimensions qui décrit les mouvements de la bille là où elle roule sans glisser ni se tordre. ${\displaystyle \mathbb {C} ^{5}}$${\displaystyle {\mathfrak {g}}_{2}}$

En 1900, Engel a découvert qu'une forme trilinéaire antisymétrique générique (ou forme 3-) sur un espace vectoriel complexe à 7 dimensions est préservée par un groupe isomorphe à la forme complexe de G ₂ .

En 1908, Cartan a mentionné que le groupe d'automorphisme des octonions est un groupe de Lie simple à 14 dimensions. En 1914, il déclara qu'il s'agissait de la forme réelle compacte de G ₂ .

Dans les livres et articles plus anciens, G ₂ est parfois noté E ₂ .

Formes réelles

Il existe 3 algèbres de Lie simples et réelles associées à ce système racinaire :

• L'algèbre de Lie réelle sous-jacente de l'algèbre de Lie complexe G ₂ a la dimension 28. Elle a une conjugaison complexe en tant qu'automorphisme externe et est simplement connexe. Le sous-groupe compact maximal de son groupe associé est la forme compacte de G ₂ .
• L'algèbre de Lie de la forme compacte est à 14 dimensions. Le groupe de Lie associé n'a pas d'automorphismes externes, pas de centre, et est simplement connexe et compact.
• L'algèbre de Lie de la forme non compacte (split) a une dimension 14. Le groupe de Lie simple associé a un groupe fondamental d'ordre 2 et son groupe d'automorphisme externe est le groupe trivial. Son sous-groupe compact maximal est SU(2) × SU(2)/(−1,−1) . Il a une double couverture non algébrique qui est simplement connectée.

Algèbre

Diagramme de Dynkin et matrice de Cartan

Le diagramme de Dynkin pour G ₂ est donné par .

Sa matrice de Cartan est :

${\displaystyle \left[{\begin{array}{rr}2&-3\\-1&2\end{array}}\right]}$

Racines de G ₂

Le système racinaire à 12 vecteurs de G 2 en 2 dimensions.

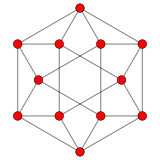La projection plane A 2 Coxeter des 12 sommets du cuboctaèdre contient le même arrangement vectoriel 2D.

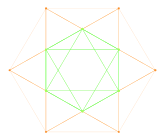Graphique de G2 en tant que sous-groupe de F4 et E8 projeté dans le plan de Coxeter

Bien qu'ils s'étendent sur un espace à 2 dimensions, tel qu'il est dessiné, il est beaucoup plus symétrique de les considérer comme des vecteurs dans un sous-espace à 2 dimensions d'un espace à trois dimensions.

(1,−1,0), (−1,1,0) (1,0,−1), (−1,0,1) (0,1,−1), (0,−1,1)

(2,−1,−1), (−2,1,1) (1,−2,1), (−1,2,−1) (1,1,−2), (−1,−1,2)

Un ensemble de racines simples , pour est:

(0,1,−1), (1,−2,1)

Groupe Weyl/Coxeter

Son Weyl / Coxeter groupe est le groupe dièdre , de l' ordre 12. Il a un degré minimal fidèle . ${\style d'affichage G=W(G_{2})}$${\style d'affichage D_{6}}$${\style d'affichage \mu (G)=5}$

Holonomie spéciale

G ₂ est l'un des groupes spéciaux possibles qui peuvent apparaître comme le groupe d' holonomie d'une métrique riemannienne . Les variétés de l' holonomie G ₂ sont aussi appelées variétés G ₂ .

Invariant polynomial

G ₂ est le groupe d'automorphismes des deux polynômes suivants en 7 variables non commutatives.

${\displaystyle C_{1}=t^{2}+u^{2}+v^{2}+w^{2}+x^{2}+y^{2}+z^{2}}$

${\displaystyle C_{2}=tuv+wtx+ywu+zyt+vzw+xvy+uxz}$ (± permutation)

qui vient de l'algèbre octonionique. Les variables doivent être non commutatives sinon le deuxième polynôme serait identique à zéro.

Générateurs

L'ajout d'une représentation des 14 générateurs avec les coefficients A , ...,  N donne la matrice :

${\displaystyle A\lambda _{1}+\cdots +N\lambda _{14}={\begin{bmatrix}0&C&-B&E&-D&-G&F-M\\-C&0&A&F&-G+N&D-K&-EL\ \B&-A&0&-N&M&L&-K\\-E&-F&N&0&-A+H&-B+I&C-J\\D&G-N&-M&A-H&0&J&I\\G&K-D&-L&B-I&-J&0&-H\\-F +M&E+L&K&-C+J&-I&H&0\end{bmatrice}}}$

C'est exactement l'algèbre de Lie du groupe

${\displaystyle G_{2}=\{g\in SO(7):g^{*}\varphi =\varphi ,\varphi =\omega ^{123}+\omega ^{145}+\omega ^{ 167}+\omega ^{246}-\omega ^{257}-\omega ^{347}-\omega ^{356}\}}$

Représentations

Les caractères des représentations de dimension finie des algèbres de Lie réelles et complexes et des groupes de Lie sont tous donnés par la formule des caractères de Weyl . Les dimensions des plus petites représentations irréductibles sont (séquence A104599 dans l' OEIS ) :

1, 7, 14, 27, 64, 77 (deux fois), 182, 189, 273, 286, 378, 448, 714, 729, 748, 896, 924, 1254, 1547, 1728, 1729, 2079 (deux fois), 2261, 2926, 3003, 3289, 3542, 4096, 4914, 4928 (deux fois), 5005, 5103, 6630, 7293, 7371, 7722, 8372, 9177, 9660, 10206, 10556, 11571, 11648, 12096, 13090….

La représentation à 14 dimensions est la représentation adjointe , et la représentation à 7 dimensions est l'action de G ₂ sur les octonions imaginaires.

Il existe deux représentations irréductibles non isomorphes de dimensions 77, 2079, 4928, 30107, etc. Les représentations fondamentales sont celles de dimensions 14 et 7 (correspondant aux deux nœuds du diagramme de Dynkin dans l'ordre tel que la triple flèche pointe de le premier au second).

Vogan (1994) a décrit les représentations unitaires irréductibles (de dimension infinie) de la forme réelle scindée de G ₂ .

Groupes finis

Le groupe G ₂ ( q ) est constitué des points du groupe algébrique G ₂ sur le corps fini F _q . Ces groupes finis ont été introduits pour la première fois par Leonard Eugene Dickson dans Dickson (1901) pour q impair et Dickson (1905) pour q pair . L'ordre de G ₂ ( q ) est q ⁶ ( q ⁶ − 1)( q ² − 1) . Lorsque q 2 , le groupe est simple , et lorsque q = 2 , il a un sous-groupe simple d' indice 2 isomorphe à ² A ₂ (3 ² ), et est le groupe d'automorphisme d'un ordre maximal des octonions. Le groupe de Janko J ₁ a d'abord été construit comme un sous-groupe de G ₂ (11). Ree (1960) a introduit les groupes de Ree torsadés ² G ₂ ( q ) d'ordre q ³ ( q ³ + 1)( q − 1) pour q = 3 ^{2 n +1} , une puissance impaire de 3.

Voir également

• Matrice de cartan
• Diagramme de Dynkin
• Algèbre de Jordanie exceptionnelle
• Représentation fondamentale
• G ₂ -structure
• Groupe de mensonges
• Produit croisé à sept dimensions
• Groupe Mensonge simple

Les références

• Adams, J. Frank (1996), Conférences sur les groupes de Lie exceptionnels , Chicago Lectures in Mathematics, University of Chicago Press , ISBN 978-0-226-00526-3, MR  1428422
• Baez, John (2002), "Les Octonions", Bull. Amer. Math. Soc. , 39 (2) : 145–205, arXiv : math/0105155 , doi : 10.1090/S0273-0979-01-00934-X.

Voir section 4.1 : G ₂ ; dont une version HTML en ligne est disponible sur http://math.ucr.edu/home/baez/octonions/node14.html .

• Bryant, Robert (1987), "Metrics with Exceptional Holonomy", Annals of Mathematics , 2, 126 (3) : 525-576, doi : 10.2307/1971360 , JSTOR  1971360
• Dickson, Leonard Eugene (1901), "Theory of Linear Groups in An Arbitrary Field", Transactions of the American Mathematical Society , Providence, RI: American Mathematical Society , 2 (4): 363-394, doi : 10.1090/S0002-9947 -1901-1500573-3 , ISSN  0002-9947 , JSTOR  1986251 , réimprimé dans le volume II de ses papiers collectésLeonard E. Dickson a signalé des groupes de type G ₂ dans des champs de caractéristiques impaires.
• Dickson, LE (1905), "Un nouveau système de groupes simples" , Math. Anne. , 60 : 137–150, doi : 10.1007/BF01447497Leonard E. Dickson a signalé des groupes de type G ₂ dans des champs de même caractéristique.
• Ree, Rimhak (1960), "Une famille de groupes simples associés à l'algèbre de Lie simple de type (G ₂ )", Bulletin of the American Mathematical Society , 66 (6) : 508-510, doi : 10.1090/S0002-9904 -1960-10523-X , ISSN  0002-9904 , MR  0125155
• Vogan, David A. Jr. (1994), « The unitary dual of G ₂ », Inventiones Mathematicae , 116 (1) : 677–791, Bibcode : 1994InMat.116..677V , doi : 10.1007/BF01231578 , ISSN  0020- 9910 , MR  1253210