Nombre d'or -Golden ratio

nombre d'or

Segments de ligne dans le nombre d'or
Représentations
Décimal	1.618 033 988 749 894 ...
Forme algébrique	${\displaystyle {\frac {1+{\sqrt {5}}}{2}}}$
Fraction continue	${\displaystyle 1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots}}}}}}} }}$
Binaire	1.1001 1110 0011 0111 0111 ...
Hexadécimal	1.9E37 79B9 7F4A 7C15 ...

Un rectangle doré avec un côté long a et un côté court b adjacent à un carré avec des côtés de longueur a produit un rectangle doré similaire avec un côté long a + b et un côté court a . Ceci illustre la relation${\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi .}$

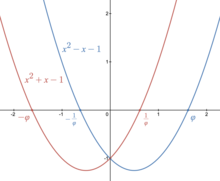
En mathématiques , deux quantités sont dans le nombre d'or si leur rapport est le même que le rapport de leur somme à la plus grande des deux quantités. Exprimé algébriquement, pour des quantités et avec${\displaystyle a}$${\displaystyle b}$${\displaystyle a>b>0,}$

${\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}\ {=:}\ \varphi }$

où la lettre grecque phi (${\displaystyle\varphi }$ ou ) représente le nombre d'or. C'est un nombre irrationnel qui est une solution à l' équation quadratique avec une valeur de ${\displaystyle\phi}$ ${\displaystyle x^{2}-x-1=0,}$

${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=}$1.618 033 988 749 .... ( OEIS :  A001622 )

Le nombre d'or est aussi appelé nombre d'or ou nombre d'or ( en latin : sectio aurea ). D'autres noms incluent le rapport extrême et moyen , la section médiale , la proportion divine (latin : proportio divina ), la section divine (latin : sectio divina ), la proportion dorée , la coupe dorée et le nombre d'or .

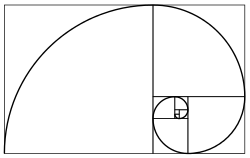
Les mathématiciens depuis Euclide ont étudié les propriétés du nombre d'or, y compris son apparition dans les dimensions d'un pentagone régulier et dans un rectangle d'or , qui peut être découpé en un carré et un rectangle plus petit avec le même rapport d'aspect . Le nombre d'or a également été utilisé pour analyser les proportions d'objets naturels ainsi que des systèmes créés par l'homme tels que les marchés financiers , dans certains cas basés sur des ajustements douteux aux données. Le nombre d'or apparaît dans certains motifs de la nature , notamment la disposition en spirale des feuilles et d'autres parties de la végétation.

Certains artistes et architectes du XXe siècle , dont Le Corbusier et Salvador Dalí , ont proportionné leurs œuvres pour se rapprocher du nombre d'or, estimant que cela était esthétique . Ceux-ci apparaissent souvent sous la forme du rectangle d'or , dans lequel le rapport du côté le plus long au plus court est le nombre d'or.

Calcul

La lettre grecque phi symbolise le nombre d'or. Habituellement, la forme minuscule ou est utilisée. Parfois, la forme majuscule est utilisée pour l' inverse du nombre d'or,${\displaystyle\varphi }$${\displaystyle\phi}$${\displaystyle \Phi}$${\displaystyle 1/\varphi .}$

Deux quantités et sont dites dans le nombre d'or si ${\displaystyle a}$${\displaystyle b}$ ${\displaystyle\varphi }$

${\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}=\varphi .}$

Une méthode pour trouver la valeur de consiste à commencer par la fraction de gauche. En simplifiant la fraction et en remplaçant dans${\displaystyle\varphi }$${\displaystyle b/a=1/\varphi ,}$

${\displaystyle {\frac {a+b}{a}}={\frac {a}{a}}+{\frac {b}{a}}=1+{\frac {b}{a}} =1+{\frac {1}{\varphi }}.}$

Donc,

${\displaystyle 1+{\frac {1}{\varphi }}=\varphi .}$

Multiplier par donne ${\displaystyle\varphi }$

${\displaystyle \varphi +1=\varphi ^{2}}$

qui peut être réorganisé en

${\displaystyle {\varphi}^{2}-\varphi -1=0.}$

En utilisant la formule quadratique , deux solutions sont obtenues :

${\displaystyle {\frac {1+{\sqrt {5}}}{2}}=1.618033\dots }$et${\displaystyle {\frac {1-{\sqrt {5}}}{2}}=-0.618033\dots .}$

Car est le rapport entre les quantités positives, est nécessairement le positif. Cependant, la racine négative, , partage de nombreuses propriétés avec le nombre d'or. ${\displaystyle\varphi }$${\displaystyle\varphi }$${\displaystyle -{\frac {1}{\varphi}}}$

Histoire

Selon Mario Livio ,

Certains des plus grands esprits mathématiques de tous les âges, de Pythagore et Euclide dans la Grèce antique , en passant par le mathématicien italien médiéval Léonard de Pise et l'astronome de la Renaissance Johannes Kepler , jusqu'aux personnalités scientifiques actuelles telles que le physicien d'Oxford Roger Penrose , ont passé des heures interminables sur ce rapport simple et ses propriétés. ... Des biologistes, des artistes, des musiciens, des historiens, des architectes, des psychologues et même des mystiques ont réfléchi et débattu sur la base de son omniprésence et de son attrait. En fait, il est probablement juste de dire que le nombre d'or a inspiré les penseurs de toutes les disciplines comme aucun autre nombre dans l'histoire des mathématiques.

—  Le nombre d'or : l'histoire de Phi, le nombre le plus étonnant du monde

Les mathématiciens de la Grèce antique ont d' abord étudié le nombre d'or en raison de son apparition fréquente en géométrie ; la division d'une ligne en "rapport extrême et moyen" (la section d'or) est importante dans la géométrie des pentagrammes et pentagones réguliers . Selon une histoire, le mathématicien Hippase du Ve siècle av. J.-C. a découvert que le nombre d'or n'était ni un nombre entier ni une fraction (un nombre irrationnel ), surprenant les Pythagoriciens . Les éléments d' Euclide ( vers 300 avant JC ) fournissent plusieurs propositions et leurs preuves en utilisant le nombre d'or, et contiennent sa première définition connue qui se déroule comme suit:

On dit qu'une ligne droite a été coupée en rapport extrême et moyen lorsque, comme toute la ligne est au plus grand segment, le plus grand est au plus petit.

Michael Maestlin , le premier à écrire une approximation décimale du rapport

Le nombre d'or a été étudié de manière périphérique au cours du prochain millénaire. Abu Kamil (vers 850–930) l'employa dans ses calculs géométriques de pentagones et de décagones ; ses écrits ont influencé ceux de Fibonacci ( Léonard de Pise ) (vers 1170-1250), qui a utilisé le rapport dans des problèmes de géométrie connexes bien qu'il ne l'ait jamais relié à la série de nombres qui porte son nom .

Luca Pacioli a nommé son livre Divina proportione ( 1509 ) d'après le rapport et a exploré ses propriétés, y compris son apparition dans certains des solides platoniciens . Léonard de Vinci , qui a illustré le livre susmentionné, a appelé le rapport la sectio aurea («section dorée»). Des mathématiciens du XVIe siècle tels que Rafael Bombelli ont résolu des problèmes géométriques en utilisant le rapport.

Le mathématicien allemand Simon Jacob (décédé en 1564) a noté que les nombres consécutifs de Fibonacci convergent vers le nombre d'or ; cela a été redécouvert par Johannes Kepler en 1608. La première approximation décimale connue du nombre d'or (inverse) a été déclarée comme "environ " en 1597 par Michael Maestlin de l ' Université de Tübingen dans une lettre à Kepler, son ancien élève. La même année, Kepler écrit à Maestlin du triangle de Kepler , qui combine le nombre d'or avec le théorème de Pythagore . Kepler a dit de ceux-ci :${\displaystyle 0.6180340}$

La géométrie a deux grands trésors : l'un est le théorème de Pythagore, l'autre la division d'une droite en raison extrême et moyenne. On peut comparer le premier à une masse d'or, le second qu'on peut appeler un joyau précieux.

Les mathématiciens du XVIIIe siècle Abraham de Moivre , Daniel Bernoulli et Leonhard Euler ont utilisé une formule basée sur le nombre d'or qui trouve la valeur d'un nombre de Fibonacci en fonction de son emplacement dans la séquence; en 1843, celle-ci fut redécouverte par Jacques Philippe Marie Binet , pour qui elle fut nommée "formule de Binet". Martin Ohm a utilisé pour la première fois le terme allemand goldener Schnitt («section dorée») pour décrire le rapport en 1835. James Sully a utilisé le terme anglais équivalent en 1875.

En 1910, le mathématicien Mark Barr a commencé à utiliser la lettre grecque Phi ( )${\displaystyle {\boldsymbol {\varphi}}}$ comme symbole du nombre d'or. Il a également été représenté par tau ( ),${\displaystyle {\boldsymbol {\tau}}}$ la première lettre du grec ancien τομή («couper» ou «section»).

Dan Shechtman fait la démonstration des quasi -cristaux au NIST en 1985 en utilisant un modèle Zometoy .

Le système de construction zome , développé par Steve Baer à la fin des années 1960, est basé sur le système de symétrie de l' icosaèdre/dodécaèdre , et utilise le nombre d'or de manière omniprésente. Entre 1973 et 1974, Roger Penrose a développé le carrelage Penrose , un motif lié au nombre d'or à la fois dans le rapport des aires de ses deux carreaux rhombiques et dans leur fréquence relative au sein du motif. Cela a conduit à la découverte par Dan Shechtman au début des années 1980 de quasi- cristaux , dont certains présentent une symétrie icosaédrique .

Demandes et observations

Architecture

L' architecte suisse Le Corbusier , célèbre pour ses contributions au style international moderne , a centré sa philosophie de conception sur des systèmes d'harmonie et de proportion. La foi de Le Corbusier dans l'ordre mathématique de l'univers était étroitement liée au nombre d'or et à la série de Fibonacci, qu'il décrivait comme « des rythmes apparents à l'œil et clairs dans leurs relations les uns avec les autres. Et ces rythmes sont à la racine même de activités humaines. Elles résonnent dans l'homme par une fatalité organique, la même belle fatalité qui fait tracer le nombre d'or par les enfants, les vieillards, les sauvages et les savants.

Le Corbusier a explicitement utilisé le nombre d'or dans son système Modulor pour l' échelle des proportions architecturales . Il considérait ce système comme une continuation de la longue tradition de Vitruve , " l'homme de Vitruve " de Léonard de Vinci , l'œuvre de Leon Battista Alberti et d'autres qui utilisaient les proportions du corps humain pour améliorer l'apparence et la fonction de l'architecture .

En plus du nombre d'or, Le Corbusier a basé le système sur les mesures humaines , les nombres de Fibonacci et l'unité double. Il a poussé la suggestion du nombre d'or dans les proportions humaines à l'extrême: il a sectionné la hauteur de son corps humain modèle au niveau du nombril avec les deux sections en nombre d'or, puis a subdivisé ces sections en nombre d'or aux genoux et à la gorge; il a utilisé ces proportions de nombre d'or dans le système Modulor . La Villa Stein de Le Corbusier de 1927 à Garches illustre l'application du système Modulor. Le plan au sol rectangulaire, l'élévation et la structure intérieure de la villa se rapprochent étroitement des rectangles dorés.

Un autre architecte suisse, Mario Botta , fonde nombre de ses créations sur des figures géométriques. Plusieurs maisons privées qu'il a conçues en Suisse sont composées de carrés et de cercles, de cubes et de cylindres. Dans une maison qu'il a conçue à Origlio , le nombre d'or est la proportion entre la partie centrale et les parties latérales de la maison.

Art

Illustration de Da Vinci d'un dodécaèdre de la Divina proportione de Pacioli ( 1509 )

Divina proportione ( Divine proportion ), un ouvrage en trois volumes de Luca Pacioli , a été publié en 1509. Pacioli, un frère franciscain , était surtout connu comme mathématicien, mais il était également formé et vivement intéressé par l'art. Divina proportione a exploré les mathématiques du nombre d'or. Bien qu'on dise souvent que Pacioli a préconisé l'application du nombre d'or pour obtenir des proportions agréables et harmonieuses, Livio souligne que l'interprétation a été attribuée à une erreur en 1799 et que Pacioli a en fait préconisé le système vitruvien de proportions rationnelles. Pacioli a également vu une signification religieuse catholique dans le rapport, ce qui a conduit au titre de son œuvre.

Les illustrations de Léonard de Vinci de polyèdres dans Divina proportione ont conduit certains à supposer qu'il a incorporé le nombre d'or dans ses peintures. Mais la suggestion que sa Joconde , par exemple, emploie des proportions de nombre d'or, n'est pas étayée par les propres écrits de Léonard. De même, bien que l' Homme de Vitruve soit souvent représenté en relation avec le nombre d'or, les proportions de la figure ne lui correspondent pas réellement, et le texte ne mentionne que des rapports de nombres entiers.

Salvador Dalí , influencé par les œuvres de Matila Ghyka , a explicitement utilisé le nombre d'or dans son chef-d'œuvre, Le Sacrement de la Cène . Les dimensions de la toile sont un rectangle doré. Un énorme dodécaèdre, en perspective pour que les bords apparaissent en nombre d'or les uns par rapport aux autres, est suspendu au-dessus et derrière Jésus et domine la composition.

Une étude statistique sur 565 œuvres d'art de différents grands peintres, réalisée en 1999, a révélé que ces artistes n'avaient pas utilisé le nombre d'or dans la taille de leurs toiles. L'étude a conclu que le rapport moyen des deux côtés des peintures étudiées est avec des moyennes pour les artistes individuels allant de (Goya) à (Bellini). D'autre part, Pablo Tosto a répertorié plus de 350 œuvres d'artistes connus, dont plus de 100 qui ont des toiles avec un rectangle doré et des proportions, et d'autres avec des proportions comme et${\displaystyle 1.34,}$${\displaystyle 1.04}$${\displaystyle 1.46}$${\displaystyle {\sqrt {5}}}$${\displaystyle {\sqrt {2}},}$ ${\displaystyle 3,}$ ${\displaystyle 4,}$${\displaystyle 6.}$

Représentation des proportions dans un manuscrit médiéval. Selon Jan Tschichold : "Proportion de page 2:3. Proportions de marge 1:1:2:3. Zone de texte proportionnée dans la Golden Section."

Livres et conception

Selon Jan Tschichold ,

Il fut un temps où les écarts par rapport aux proportions de page vraiment belles et à la section dorée étaient rares. De nombreux livres produits entre 1550 et 1770 montrent exactement ces proportions, au demi-millimètre près.${\displaystyle 2\mathbin {:} 3,}$ ${\displaystyle 1\mathbin {:} {\sqrt {3}},}$

Selon certaines sources, le nombre d'or est utilisé dans la conception de tous les jours, par exemple dans les proportions de cartes à jouer, de cartes postales, d'affiches, de plaques d'interrupteurs et de téléviseurs à écran large.

Drapeaux

Le drapeau du Togo , dont le rapport d'aspect utilise le nombre d'or

Le rapport d' aspect (rapport hauteur sur largeur) du drapeau du Togo est dans le nombre d'or.

La musique

Ernő Lendvai analyse les œuvres de Béla Bartók comme étant basées sur deux systèmes opposés, celui du nombre d'or et celui de l' échelle acoustique , bien que d'autres spécialistes de la musique rejettent cette analyse. Le compositeur français Erik Satie a utilisé le nombre d'or dans plusieurs de ses pièces, dont Sonneries de la Rose+Croix . Le nombre d'or se manifeste également dans l'organisation des sections de la musique des Reflets dans l'eau de Debussy , d' après Images ( 1ère série, 1905), où « la suite des tonalités est marquée par les intervalles 34, 21, 13 et 8, et le point culminant principal se situe à la position phi ».

Le musicologue Roy Howat a observé que les limites formelles de La Mer de Debussy correspondent exactement au nombre d'or. Trezise trouve les preuves intrinsèques "remarquables", mais prévient qu'aucune preuve écrite ou rapportée ne suggère que Debussy a consciemment recherché de telles proportions.

Bien que Heinz Bohlen ait proposé l' échelle de 833 cents sans répétition d'octave basée sur des tons combinés , l'accord présente des relations basées sur le nombre d'or. En tant qu'intervalle musical, le rapport 1,618... est de 833,090... cents ( Play ( aide · info ) ).  

Nature

Détail de l'usine de soucoupe, Aeonium tabuliforme , montrant l'arrangement en spirale multiple ( parastichy )

Johannes Kepler a écrit que "l'image de l'homme et de la femme découle de la proportion divine. À mon avis, la propagation des plantes et les actes progéniteurs des animaux sont dans le même rapport".

Le psychologue Adolf Zeising a noté que le nombre d'or est apparu dans la phyllotaxie et a soutenu à partir de ces modèles dans la nature que le nombre d'or était une loi universelle. Zeising a écrit en 1854 sur une loi orthogénétique universelle de "la recherche de la beauté et de l'exhaustivité dans les domaines de la nature et de l'art".

Cependant, certains ont fait valoir que de nombreuses manifestations apparentes du nombre d'or dans la nature, en particulier en ce qui concerne les dimensions animales, sont fictives.

Optimisation

Le nombre d'or est un élément essentiel de la recherche de nombre d'or .

Mathématiques

Irrationalité

Le nombre d'or est un nombre irrationnel . Voici deux courtes preuves de l'irrationalité :

Contradiction d'une expression dans les termes les plus bas

Si étaient rationnel , alors ce serait le rapport des côtés d'un rectangle avec des côtés entiers (le rectangle comprenant le diagramme entier). Mais ce serait aussi un rapport des côtés entiers du plus petit rectangle (la partie la plus à droite du diagramme) obtenu en supprimant un carré. La séquence de longueurs de côtés entières décroissantes formées en supprimant des carrés ne peut pas être poursuivie indéfiniment car les entiers positifs ont une borne inférieure, donc ne peuvent pas être rationnels.${\displaystyle\varphi }$${\displaystyle\varphi }$

Rappeler que:

Si nous appelons le tout et la partie la plus longue , la deuxième déclaration ci-dessus devient ${\displaystyle n}$${\displaystyle m,}$

${\displaystyle n}$c'est comme c'est${\displaystyle m}$${\displaystyle m}$${\displaystyle nm.}$

Dire que le nombre d'or est rationnel signifie que c'est une fraction où et sont des nombres entiers. Nous pouvons considérer que nous sommes dans les termes les plus bas et que nous sommes positifs. Mais si est en termes les plus bas, alors la valeur égale est en termes encore inférieurs. C'est une contradiction qui découle de l'hypothèse qui est rationnelle. ${\displaystyle\varphi }$${\displaystyle\varphi }$${\displaystyle n/m}$${\displaystyle n}$${\displaystyle m}$${\displaystyle n/m}$${\displaystyle n}$${\displaystyle m}$${\displaystyle n/m}$${\displaystyle m/(nm)}$${\displaystyle\varphi }$

Par irrationalité de${\displaystyle {\sqrt {5}}}$

Une autre preuve courte - peut-être plus connue - de l'irrationalité du nombre d'or utilise la fermeture des nombres rationnels sous l'addition et la multiplication. Si est rationnel, alors est aussi rationnel, ce qui est une contradiction si l'on sait déjà que la racine carrée d'un nombre naturel non carré est irrationnelle. ${\displaystyle \varphi ={\tfrac {1}{2}}(1+{\sqrt {5}})}$${\displaystyle 2\varphi -1={\sqrt {5}}}$

Polynôme minimal

Le nombre d'or et son inverse négatif sont les deux racines du polynôme quadratique . Le nombre d'or négatif et réciproque sont les deux racines du polynôme quadratique .${\displaystyle\varphi }$${\displaystyle -\varphi ^{-1}}$ ${\displaystyle x^{2}-x-1}$${\displaystyle -\varphi }$${\displaystyle \varphi ^{-1}}$${\displaystyle x^{2}+x-1}$

Le nombre d'or est aussi un nombre algébrique et même un entier algébrique . Il a un polynôme minimal

${\displaystyle x^{2}-x-1.}$

Ce polynôme quadratique a deux racines , et${\displaystyle\varphi }$${\displaystyle -\varphi ^{-1}.}$

Le nombre d'or est également étroitement lié au polynôme

${\displaystyle x^{2}+x-1,}$

qui a des racines et${\displaystyle -\varphi }$${\displaystyle\varphi ^{-1}.}$

Nombre d'or conjugué

La racine conjuguée du polynôme minimal est ${\displaystyle x^{2}-x-1}$

${\displaystyle -{\frac {1}{\varphi }}=1-\varphi ={\frac {1-{\sqrt {5}}}{2}}=-0.618033\dots .}$

La valeur absolue de cette quantité ( )${\displaystyle 0.618\ldots}$ correspond au rapport de longueur pris dans l'ordre inverse (longueur de segment plus courte sur longueur de segment plus longue, ), et est parfois appelée nombre d' or conjugué ou rapport d'argent . Il est désigné ici par le Phi majuscule ( ) :${\displaystyle b/a}$${\displaystyle {\boldsymbol {\Phi}}}$

${\displaystyle \Phi ={\frac {1}{\varphi }}=\varphi ^{-1}=\varphi -1=0.618033\ldots .}$

Cela illustre la propriété unique du nombre d'or parmi les nombres positifs, que

${\displaystyle {\frac {1}{\varphi }}=\varphi -1,}$

ou son inverse :

${\displaystyle {\frac {1}{\Phi }}=\Phi +1.}$

Formes alternatives

Approximations du nombre d'or réciproque par des fractions continues finies ou des rapports de nombres de Fibonacci

La formule peut être développée de manière récursive pour obtenir une fraction continue pour le nombre d'or : ${\displaystyle \varphi =1+1/\varphi }$

${\displaystyle \varphi =[1;1,1,1,\dots ]=1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}$

et sa réciproque :

${\displaystyle \varphi ^{-1}=[0;1,1,1,\dots ]=0+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1} {1+\ddots }}}}}}}$

Les convergentes de ces fractions continues (${\displaystyle 1/1,}$ ... ou ...) sont des rapports de nombres de Fibonacci successifs . ${\displaystyle 2/1,}$ ${\displaystyle 2/1,}$ ${\displaystyle 3/2,}$ ${\displaystyle 5/3,}$ ${\displaystyle 8/5,}$ ${\displaystyle 13/8,}$${\displaystyle 1/1,}$ ${\displaystyle 1/2,}$ ${\displaystyle 2/3,}$ ${\displaystyle 3/5,}$ ${\displaystyle 5/8,}$ ${\displaystyle 8/13,}$

L'équation produit également la racine carrée continue : ${\displaystyle \varphi ^{2}=1+\varphi }$

${\displaystyle \varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+\cdots}}}}}}.}$

Une série infinie peut être dérivée pour exprimer : ${\displaystyle\varphi }$

${\displaystyle \varphi ={\frac {13}{8}}+\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}(2n+1) ! }{4^{2n+3}n!(n+2) !}}.}$

Également:

${\displaystyle {\begin{aligned}\varphi &=1+2\sin(\pi /10)=1+2\sin 18^{\circ },\\[5mu]\varphi &={\tfrac { 1}{2}}\csc(\pi /10)={\tfrac {1}{2}}\csc 18^{\circ },\\[5mu]\varphi &=2\cos(\pi / 5)=2\cos 36^{\circ },\\[5mu]\varphi &=2\sin(3\pi /10)=2\sin 54^{\circ }.\end{aligned}}}$

Celles-ci correspondent au fait que la longueur de la diagonale d'un pentagone régulier est multipliée par la longueur de son côté, et des relations similaires dans un pentagramme . ${\displaystyle\varphi }$

Géométrie

Spirales dorées approximatives et vraies . La spirale verte est constituée de quarts de cercles tangents à l'intérieur de chaque carré, tandis que la spirale rouge est une spirale dorée, un type particulier de spirale logarithmique . Les parties qui se chevauchent apparaissent en jaune . La longueur du côté d'un carré divisée par celle du carré plus petit suivant est le nombre d'or.

Le nombre revient souvent en géométrie , notamment dans les figures à symétrie pentagonale . La longueur de la diagonale d'un pentagone régulier est multipliée par son côté. Les sommets d'un icosaèdre régulier sont ceux de trois rectangles dorés mutuellement orthogonaux .${\displaystyle\varphi }$${\displaystyle\varphi }$

Il n'y a pas d' algorithme général connu pour disposer un nombre donné de nœuds uniformément sur une sphère, pour l'une des nombreuses définitions de distribution paire (voir, par exemple, le problème de Thomson ou le problème de Tammes ). Cependant, une approximation utile résulte de la division de la sphère en bandes parallèles de surface égale et du placement d'un nœud dans chaque bande à des longitudes espacées par une section d'or du cercle, c'est-à-dire que cette méthode a été utilisée pour disposer les 1500 miroirs de l'étudiant-participatif. satellite Starshine-3 . ${\displaystyle 360^{\circ }/\varphi \approx 222.5^{\circ }.}$

Division d'un segment de ligne par division intérieure

Diviser un segment de ligne par division intérieure selon le nombre d'or

1. Avoir un segment de droite construire une perpendiculaire au point avec la moitié de la longueur de Dessiner l' hypoténuse${\displaystyle AB,}$${\displaystyle BC}$${\ style d'affichage B,}$${\displaystyle BC}$${\displaystyle AB.}$ ${\displaystyle AC.}$
2. Dessine un arc de centre et de rayon Cet arc coupe l'hypoténuse au point${\displaystyle C}$${\displaystyle BC.}$${\displaystyle CA}$${\displaystyle D.}$
3. Dessiner un arc avec centre et rayon Cet arc coupe le segment de ligne d'origine au point Point divise le segment de ligne d'origine en segments de ligne et avec des longueurs dans le nombre d'or.${\displaystyle A}$${\displaystyle AD.}$${\displaystyle AB}$${\displaystyle S.}$${\displaystyle S}$${\displaystyle AB}$${\displaystyle AS}$${\displaystyle SB}$

Diviser un segment de ligne par une division extérieure

Diviser un segment de ligne par une division extérieure selon le nombre d'or

1. Tracez un segment de droite et construisez à partir de ce point un segment perpendiculaire et de même longueur que${\displaystyle AS}$${\displaystyle S}$${\displaystyle SC}$${\displaystyle AS}$${\displaystyle AS.}$
2. Coupez le segment de ligne en deux avec${\displaystyle AS}$${\displaystyle M.}$
3. Un arc de cercle autour de rayon coupe en point la ligne droite passant par les points et (également appelée extension de ). Le rapport de au segment construit est le nombre d'or.${\displaystyle M}$${\displaystyleMC}$${\displaystyle B}$${\displaystyle A}$${\displaystyle S}$${\displaystyle AS}$${\displaystyle AS}$${\displaystyle SB}$

Des exemples d'application que vous pouvez voir dans les articles Pentagone avec une longueur de côté donnée , Decagon avec un cercle circonscrit donné et Decagon avec une longueur de côté donnée .

Les deux algorithmes différents affichés ci-dessus produisent des constructions géométriques qui déterminent deux segments de ligne alignés où le rapport du plus long au plus court est le nombre d'or.

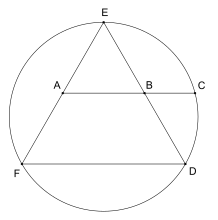
Triangle d'or, pentagone et pentagramme

Triangle d'or . L'angle à double arc rouge est ou radians.${\displaystyle 36^{\circ }}$${\displaystyle {\tfrac {1}{5}}\pi }$

Triangle d'or

Le triangle d'or peut être caractérisé comme un triangle isocèle avec la propriété que la bissectrice de l'angle produit un nouveau triangle qui est un triangle similaire à l'original. ${\displaystyle ABC}$${\displaystyle C}$ ${\displaystyle CXB}$

Si angle alors à cause de la bissection, et à cause des triangles semblables ; de la symétrie isocèle originelle, et par similarité. Les angles d'un triangle s'additionnent pour donner donc les angles du triangle d'or sont donc - - Les angles du triangle isocèle obtus restant (parfois appelé le gnomon d'or) sont - -${\displaystyle BCX=\alpha ,}$${\displaystyle XCA=\alpha }$${\displaystyle CAB=\alpha }$${\displaystyle ABC=2\alpha }$${\displaystyle BXC=2\alpha }$${\displaystyle 180^{\circ },}$${\displaystyle 5\alpha =180^{\circ },}$${\displaystyle \alpha =36^{\circ }.}$${\displaystyle 36^{\circ }}$${\displaystyle 72^{\circ }}$${\displaystyle 72^{\circ }.}$${\displaystyle AXC}$${\displaystyle 36^{\circ }}$${\displaystyle 36^{\circ }}$${\displaystyle 108^{\circ }.}$

Supposons qu'il ait une longueur et que nous appelons la longueur En raison des triangles isocèles et donc ceux-ci sont également de longueur Longueur donc égale Mais le triangle est similaire au triangle tel et tel également égal Ainsi confirmant que c'est bien le nombre d'or. ${\displaystyle XB}$${\displaystyle 1,}$${\displaystyle BC}$${\displaystyle\varphi .}$${\displaystyle XC=XA}$${\displaystyle BC=XC,}$${\displaystyle\varphi .}$${\displaystyle AC=AB,}$${\displaystyle\varphi +1.}$${\displaystyle ABC}$${\displaystyle CXB,}$${\displaystyle AC/BC=BC/BX,}$ ${\displaystyle AC/\varphi =\varphi /1,}$${\displaystyle CA}$${\displaystyle\varphi ^{2}.}$${\displaystyle \varphi ^{2}=\varphi +1,}$${\displaystyle\varphi }$

De même, le rapport de l'aire du plus grand triangle au plus petit est égal à tandis que le rapport inverse est${\displaystyle AXC}$${\displaystyle CXB}$${\displaystyle \varphi ,}$${\displaystyle\varphi -1.}$

Pentagone

Dans un pentagone régulier , le rapport d'une diagonale à un côté est le nombre d'or, tandis que les diagonales qui se croisent se coupent dans le nombre d'or.

La construction d'Odom

Soit et être les milieux des côtés et d'un triangle équilatéral Prolonger pour rencontrer le cercle circonscrit d' au${\displaystyle A}$${\displaystyle B}$${\displaystyle EF}$${\displaystyle ED}$${\displaystyle DÉF.}$${\displaystyle AB}$${\displaystyle DEF}$${\displaystyle C.}$

${\displaystyle {\tfrac {|AB|}{|BC|}}={\tfrac {|AC|}{|AB|}}=\phi }$

George Odom a donné une construction remarquablement simple pour impliquer un triangle équilatéral : si un triangle équilatéral est inscrit dans un cercle et que le segment de droite joignant les milieux de deux côtés est produit pour couper le cercle en l'un ou l'autre de deux points, alors ces trois points sont en proportion d'or. Ce résultat est une conséquence directe du théorème des accords d'intersection et peut être utilisé pour construire un pentagone régulier, une construction qui a attiré l'attention du célèbre géomètre canadien HSM Coxeter qui l'a publié au nom d'Odom sous forme de diagramme dans l' American Mathematical Monthly accompagné de le seul mot "Voici!" ${\displaystyle\varphi }$

Pentacle

Un pentagramme coloré pour distinguer ses segments de ligne de différentes longueurs. Les quatre longueurs sont en nombre d'or les unes par rapport aux autres.

Le nombre d'or joue un rôle important dans la géométrie des pentagrammes . Chaque intersection d'arêtes sectionne d'autres arêtes dans le nombre d'or. De plus, le rapport de la longueur du segment le plus court au segment délimité par les deux arêtes qui se croisent (un côté du pentagone au centre du pentagramme) est comme le montre l'illustration en quatre couleurs. ${\displaystyle \varphi ,}$

Le pentagramme comprend dix triangles isocèles : cinq triangles isocèles aigus et cinq obtus . Dans chacun d'eux, le rapport du côté le plus long au côté le plus court est Les triangles aigus sont des triangles d'or. Les triangles isocèles obtus sont des gnomons dorés. ${\displaystyle\varphi .}$

Théorème de Ptolémée

Le nombre d'or dans un pentagone régulier peut être calculé à l'aide du théorème de Ptolémée .

Les propriétés du nombre d'or d'un pentagone régulier peuvent être confirmées en appliquant le théorème de Ptolémée au quadrilatère formé en supprimant l'un de ses sommets. Si le bord long et les diagonales du quadrilatère sont et les bords courts sont alors le théorème de Ptolémée donne ce qui donne ${\displaystyle b,}$${\displaystyle a,}$${\displaystyle b^{2}=a^{2}+ab}$

${\displaystyle {b \over a}={{1+{\sqrt {5}}} \over 2}.}$

Scalenité des triangles

Considérons un triangle dont les côtés sont de longueurs et dans l'ordre décroissant. Définissez la "scalénité" du triangle comme étant le plus petit des deux rapports et La scalénité est toujours inférieure à et peut être rendue aussi proche que souhaité de${\displaystyle a,}$ ${\displaystyle b,}$${\displaystyle c}$${\displaystyle a/b}$${\displaystyle b/c.}$${\displaystyle\varphi }$${\displaystyle\varphi .}$

Triangle dont les côtés forment une progression géométrique

Si les longueurs des côtés d'un triangle forment une progression géométrique et sont dans le rapport où est le rapport commun, alors doivent se situer dans la plage en conséquence de l' inégalité du triangle (la somme de deux côtés d'un triangle doit être strictement supérieure à la longueur du troisième côté). Si alors les deux côtés les plus courts sont et mais leur somme est donc Un calcul similaire montre qu'un triangle dont les côtés sont dans le rapport est un triangle rectangle (car ) appelé triangle de Kepler . ${\displaystyle 1\mathbin {:} r\mathbin {:} r^{2},}$${\displaystyle r}$${\displaystyle r}$${\displaystyle \varphi -1<r<\varphi ,}$${\displaystyle r=\varphi }$${\displaystyle 1}$${\displaystyle\varphi }$${\displaystyle \varphi ^{2},}$${\displaystyle r<\varphi .}$${\displaystyle r>\varphi -1.}$${\displaystyle 1\mathbin {:} {\sqrt {\varphi }}\mathbin {:} \varphi }$${\displaystyle 1+\varphi =\varphi ^{2}}$

Triangle d'or, losange et triacontaèdre rhombique

L'un des losanges du triacontaèdre rhombique

Toutes les faces du triacontaèdre rhombique sont des losanges dorés

Un losange doré est un losange dont les diagonales sont dans le nombre d'or. Le triacontaèdre rhombique est un polytope convexe qui possède une propriété bien particulière : toutes ses faces sont des losanges dorés. Dans le triacontaèdre rhombique , l' angle dièdre entre deux losanges adjacents est égal à deux fois l'angle isocèle d'un triangle d'or et quatre fois son angle le plus aigu. ${\displaystyle 144^{\circ },}$

Relation avec la suite de Fibonacci

Les mathématiques du nombre d'or et de la suite de Fibonacci sont intimement liées. La suite de Fibonacci est :

${\displaystyle 1,}$ ${\displaystyle 1,}$ ${\displaystyle 2,}$ ${\displaystyle 3,}$ ${\displaystyle 5,}$ ${\displaystyle 8,}$ ${\displaystyle 13,}$ ${\displaystyle 21,}$ ${\displaystyle 34,}$ ${\displaystyle 55,}$ ${\displaystyle 89,}$ ${\displaystyle 144,}$ ${\displaystyle 233,}$ ${\displaystyle 377,}$ ${\displaystyle 610,}$ ${\displaystyle 987,}$...

Une expression de forme fermée pour la suite de Fibonacci implique le nombre d'or :

${\displaystyle F\left(n\right)={{\varphi ^{n}-(1-\varphi )^{n}} \over {\sqrt {5}}}={{\varphi ^{n }-(-\varphi )^{-n}} \over {\sqrt {5}}}.}$

Une spirale de Fibonacci qui se rapproche de la spirale dorée, en utilisant des tailles de carrés de séquence de Fibonacci jusqu'à La spirale est dessinée à partir du carré intérieur et continue vers l'extérieur vers des carrés successivement plus grands.${\displaystyle 34.}$${\displaystyle 1\fois 1}$

Le nombre d'or est la limite des rapports des termes successifs de la suite de Fibonacci (ou de toute suite de type Fibonacci), comme le montre Kepler :

${\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\varphi .}$

En d'autres termes, si un nombre de Fibonacci est divisé par son prédécesseur immédiat dans la séquence, le quotient se rapproche , par exemple, ces approximations sont alternativement inférieures et supérieures à et convergent vers à mesure que les nombres de Fibonacci augmentent, et : ${\displaystyle\varphi ;}$${\displaystyle 987/610\environ 1.6180327868852.}$${\displaystyle \varphi ,}$${\displaystyle\varphi }$

${\displaystyle \sum _{n=1}^{\infty}|F_{n}\varphi -F_{n+1}|=\varphi .}$

Plus généralement

${\displaystyle \lim _{n\to \infty }{\frac {F_{n+a}}{F_{n}}}=\varphi ^{a},}$

où ci-dessus, les rapports des termes consécutifs de la suite de Fibonacci, est un cas où${\displaystyle a=1.}$

De plus, les puissances successives de obéissent à la récurrence de Fibonacci${\displaystyle\varphi }$

${\displaystyle \varphi ^{n+1}=\varphi ^{n}+\varphi ^{n-1}.}$

Cette identité permet de réduire tout polynôme en une expression linéaire. Par exemple: ${\displaystyle\varphi }$

${\displaystyle {\begin{aligned}3\varphi ^{3}-5\varphi ^{2}+4&=3(\varphi ^{2}+\varphi )-5\varphi ^{2}+4\ \&=3[(\varphi +1)+\varphi ]-5(\varphi +1)+4\\&=\varphi +2\environ 3,618033.\end{aligné}}}$

La réduction à une expression linéaire peut être accomplie en une seule étape en utilisant la relation

${\displaystyle \varphi ^{k}=F_{k}\varphi +F_{k-1},}$

où est le ème nombre de Fibonacci. ${\displaystyle F_{k}}$${\displaystyle k}$

Cependant, ce n'est pas une propriété spéciale de car les polynômes de toute solution d'une équation quadratique peuvent être réduits de manière analogue, en appliquant : ${\displaystyle \varphi ,}$${\style d'affichage x}$

${\displaystyle x^{2}=ax+b}$

pour des coefficients donnés tels que satisfait l'équation. Plus généralement encore, toute fonction rationnelle (avec des coefficients rationnels) de la racine d'un polynôme irréductible de ème degré sur les rationnels peut être réduite à un polynôme de degré Phrasé en termes de théorie des champs , si est une racine d'un irréductible de degré e polynôme, puis a un degré supérieur avec une base${\displaystyle a,}$ ${\displaystyle b}$${\style d'affichage x}$${\displaystyle n}$${\displaystyle n-1.}$${\displaystyle\alpha}$${\displaystyle n}$${\displaystyle \mathbb {Q} (\alpha)}$${\displaystyle n}$${\displaystyle \mathbb {Q} ,}$${\displaystyle \{1,\alpha ,\ldots ,\alpha ^{n-1}\}.}$

Symétries

Le nombre d'or et le nombre d'or inverse ont un ensemble de symétries qui les préservent et les relient. Ils sont tous deux préservés par les transformations linéaires fractionnaires - ce fait correspond à l'identité et à la définition de l'équation quadratique. De plus, ils sont interchangés par les trois cartes - ils sont réciproques, symétriques autour et (projectivement) symétriques autour${\displaystyle \varphi _{\pm }={\tfrac {1}{2}}{\bigl (}1\pm {\sqrt {5}}{\bigr )}}$ ${\displaystyle x,1/(1-x),(x-1)/x}$${\displaystyle 1/x,1-x,x/(x-1)}$${\displaystyle {\tfrac {1}{2}},}$${\displaystyle 2.}$

Plus profondément, ces applications forment un sous-groupe du groupe modulaire isomorphe au groupe symétrique sur les lettres, correspondant au stabilisateur de l'ensemble des points étalons sur la droite projective , et les symétries correspondent à l'application quotient – ​​le sous-groupe constitué par l'identité et les -cycles, en notation cyclique, fixent les deux nombres, tandis que les -cycles les échangent , réalisant ainsi la carte. ${\displaystyle \operatorname {PSL} (2,\mathbb {Z} )}$${\displaystyle 3}$${\displaystyle S_{3},}$${\style d'affichage \{0,1,\infty \}}$${\displaystyle 3}$${\displaystyle S_{3}\à S_{2}}$${\displaystyle C_{3}<S_{3}}$${\displaystyle 3}$ ${\displaystyle \{(1),(0\,1\,\infty ),(0\,\infty \,1)\},}$${\displaystyle 2}$${\displaystyle \{(0\,1),(0\,\infty ),(1\,\infty )\}}$

Autres propriétés

Le nombre d'or a l'expression la plus simple (et la convergence la plus lente) en tant qu'expansion de fraction continue de tout nombre irrationnel (voir Formes alternatives ci-dessus). C'est, pour cette raison, l'un des pires cas du théorème d'approximation de Lagrange et c'est un cas extrême de l' inégalité de Hurwitz pour les approximations diophantiennes . C'est peut-être la raison pour laquelle des angles proches du nombre d'or apparaissent souvent dans la phyllotaxie .

Le polynôme quadratique de définition et la relation conjuguée conduisent à des valeurs décimales qui ont leur partie fractionnaire en commun avec : ${\displaystyle\varphi }$

${\displaystyle {\begin{aligned}\varphi ^{2}&=\varphi +1=2.618033\dots ,\\[5mu]{\frac {1}{\varphi }}&=\varphi -1=0.618033 \points .\end{aligné}}}$

La suite des puissances de contient ces valeurs plus généralement, toute puissance de est égale à la somme des deux puissances immédiatement précédentes : ${\displaystyle\varphi }$${\displaystyle 0.618033\ldots ,}$ ${\displaystyle 1.0,}$ ${\displaystyle 1.618033\ldots ,}$ ${\displaystyle 2.618033\ldots ;}$${\displaystyle\varphi }$

${\displaystyle \varphi ^{n}=\varphi ^{n-1}+\varphi ^{n-2}=\varphi \cdot \operatorname {F} _{n}+\operatorname {F} _{n -1}.}$

Par conséquent, on peut facilement décomposer n'importe quelle puissance de en un multiple de et une constante. Le multiple et la constante sont toujours des nombres de Fibonacci adjacents. Cela conduit à une autre propriété des puissances positives de : ${\displaystyle\varphi }$${\displaystyle\varphi }$${\displaystyle\varphi }$

Si alors : ${\displaystyle \lfloor n/2-1\rfloor =m,}$

${\displaystyle {\begin{aligned}\varphi ^{n}&=\varphi ^{n-1}+\varphi ^{n-3}+\cdots +\varphi ^{n-1-2m}+\ varphi ^{n-2-2m}\\[5mu]\varphi ^{n}-\varphi ^{n-1}&=\varphi ^{n-2}.\end{aligned}}}$

Le nombre d'or est une unité fondamentale du corps des nombres algébriques et est un nombre de Pisot-Vijayaraghavan . Dans le champ nous avons où est le -ème numéro de Lucas . ${\displaystyle \mathbb {Q} ({\sqrt {5}})}$${\displaystyle \mathbb {Q} ({\sqrt {5}})}$${\displaystyle \varphi ^{n}={\tfrac {1}{2}}{\bigl (}L_{n}+F_{n}{\sqrt {5}}{\bigr )},}$${\displaystyle L_{n}}$${\displaystyle n}$

Lorsque le nombre d'or est utilisé comme base d'un système numérique (voir base du nombre d'or , parfois surnommé phinary ou -nary ), les nombres entiers quadratiques dans l'anneau - c'est-à-dire les nombres de la forme pour - ont des représentations terminales , mais les fractions rationnelles ont représentations non terminales. ${\displaystyle\varphi }$${\displaystyle \mathbb {Z} [\varphi ]}$${\displaystyle a+b\varphi }$${\displaystyle a,b\in \mathbb {Z} }$

Le nombre d'or apparaît également en géométrie hyperbolique , comme la distance maximale d'un point d'un côté d'un triangle idéal au plus proche des deux autres côtés : cette distance, la longueur du côté du triangle équilatéral formé par les points de tangence d'un cercle inscrit dans le triangle idéal, est${\displaystyle 4\mathbin {:} \log(\varphi ).}$

Le nombre d'or apparaît également dans la théorie des fonctions modulaires . Pour , laissez ${\displaystyle \left|q\right|<1}$

${\displaystyle R(q)={\cfrac {q^{1/5}}{1+{\cfrac {q}{1+{\cfrac {q^{2}}{1+{\cfrac {q ^{3}}{1+\ddots }}}}}}}}.}$

Puis

${\displaystyle R(e^{-2\pi })={\sqrt {\varphi {\sqrt {5}}}}-\varphi ,\quad R(-e^{-\pi })=\varphi ^{-1}-{\sqrt {2-\varphi ^{-1}}}}$

et

${\displaystyle R(e^{-2\pi i/\tau })={\frac {1-\varphi R(e^{2\pi i\tau })}{\varphi +R(e^{ 2\pi i\tau })}}}$

où et dans la fraction continue doivent être évalués comme . La fonction est invariante sous , un sous-groupe de congruence du groupe modulaire . Aussi pour les nombres réels positifs , puis ${\displaystyle \operatorname {Je} \tau >0}$${\displaystyle (e^{z})^{1/5}}$${\displaystyle e^{z/5}}$${\displaystyle \tau \mapsto R(e^{2\pi i\tau })}$${\displaystyle\Gamma (5)}$ ${\displaystyle a,b\in \mathbb {R} ^{+}}$${\displaystyle ab=\pi ^{2},}$

${\displaystyle (\varphi +R(e^{-2a}))(\varphi +R(e^{-2b}))=\varphi {\sqrt {5}}}$

et

${\displaystyle (\varphi ^{-1}-R(-e^{-a}))(\varphi ^{-1}-R(-e^{-b}))=\varphi ^{-1 }{\sqrt {5}}.}$

Pour la fonction gamma , les seules solutions à l'équation Γ( z − 1) = Γ( z + 1) sont z = φ et z = −1/ φ .

Développement décimal

L'expansion décimale du nombre d'or peut être calculée à partir de l'expression

${\displaystyle \varphi ={1+{\sqrt {5}} \over 2}}$

avec${\displaystyle {\sqrt {5}}=}$ 2.236 067 977 .... OEIS :  A002163 . La racine carrée de${\displaystyle 5}$ peut être calculée via la méthode babylonienne , en commençant par une estimation initiale telle queet en itérant${\style d'affichage x_{0}=2}$

${\displaystyle x_{n+1}={\frac {1}{2}}\left(x_{n}+{\frac {5}{x_{n}}}\right)}$

jusqu'à ce que la différence entre et devienne zéro au nombre de chiffres souhaité. Puis${\displaystyle n=0,1,2,3,\ldots ,}$${\style d'affichage x_{n}}$${\displaystyle x_{n-1}}$${\displaystyle \varphi \approx {\tfrac {1}{2}}(1+x_{n}).}$

L'algorithme babylonien pour est équivalent à la méthode de Newton pour résoudre l'équation et il converge quadratiquement , ce qui signifie que le nombre de chiffres corrects est à peu près doublé à chaque itération. ${\displaystyle {\sqrt {5}}}$${\displaystyle x^{2}-5=0,}$

Pour éviter l'opération de division coûteuse en calcul, la méthode de Newton peut à la place être utilisée pour résoudre l'équation de la racine Alors et l'étape de mise à jour est ${\displaystyle 5x^{-2}-4=0}$${\textstyle {\tfrac {1}{2}}{\sqrt {5}}.}$${\textstyle \varphi \approx {\tfrac {1}{2}}+x_{n}}$

${\displaystyle x_{n+1}={\tfrac {3}{2}}x_{n}-{\tfrac {2}{5}}x_{n}^{3}.}$

Alternativement, la méthode de Newton peut être appliquée directement à toute équation qui a le nombre d'or comme solution, comme Dans ce cas, et l'étape de mise à jour est ${\displaystyle x^{2}-x-1=0.}$${\textstyle \varphi \environ x_{n}}$

${\displaystyle x_{n+1}={\frac {x_{n}^{2}+1}{2x_{n}-1}}\,.}$

La méthode de Halley a une convergence cubique (triplant environ le nombre de chiffres corrects à chaque itération), mais peut être plus lente pour le calcul pratique car chaque étape demande plus de travail. Pour résoudre l'étape de mise à jour est ${\displaystyle x^{2}-x-1=0,}$

${\displaystyle x_{n+1}={\frac {x_{n}^{3}+3x_{n}-1}{3x_{n}^{2}-3x_{n}+2}}\, .}$

Le nombre d'or est donc relativement facile à calculer avec une précision arbitraire . Le temps nécessaire pour calculer les chiffres du nombre d'or est proportionnel au temps nécessaire pour diviser les nombres à deux chiffres. C'est considérablement plus rapide que les algorithmes connus pour les nombres transcendantaux et . ${\displaystyle n}$${\displaystyle n}$ ${\style d'affichage \pi}$${\displaystyle e}$

Une alternative facilement programmable utilisant uniquement l'arithmétique entière consiste à calculer deux grands nombres de Fibonacci consécutifs et à les diviser. Le rapport des nombres de Fibonacci et chacun sur les chiffres donne plus de chiffres significatifs du nombre d'or. ${\displaystyle F_{25001}}$${\displaystyle F_{25000},}$${\displaystyle 5000}$${\displaystyle 10{,}000}$

L'expansion décimale du nombre d'or a été calculée avec une précision de dix billions ( ) chiffres. ${\displaystyle\varphi }$${\displaystyle 1\fois 10^{13}=10{,}000{,}000{,}000{,}000}$

Pyramides

Une pyramide carrée régulière est déterminée par son triangle rectangle médial, dont les bords sont l'apothème de la pyramide ( ),${\displaystyle a}$ la demi-base ( )${\displaystyle b}$ et la hauteur ( ); ${\displaystyle h}$l'angle d'inclinaison du visage est également marqué. Les proportions mathématiques de et et présentent un intérêt particulier par rapport aux pyramides égyptiennes.${\displaystyle b\mathbin {:} h\mathbin {:} a}$${\displaystyle 1\mathbin {:} {\sqrt {\varphi }}\mathbin {:} \varphi }$${\displaystyle 3\mathbin {:} 4\mathbin {:} 5}$${\displaystyle 1\mathbin {:} 4/\pi \mathbin {:} 1.61899}$

Les pyramides égyptiennes et les pyramides carrées régulières qui leur ressemblent peuvent être analysées en fonction du nombre d'or et d'autres rapports.

Pyramides mathématiques

Une pyramide dans laquelle l'apothème (hauteur oblique le long de la bissectrice d'un visage) est égale à fois la demi-base (la moitié de la largeur de la base) est parfois appelée une pyramide dorée . Le triangle isocèle qui est la face d'une telle pyramide peut être construit à partir des deux moitiés d'un rectangle doré divisé en diagonale (de taille demi-base par apothème), joignant les arêtes de longueur moyenne pour former l'apothème. La hauteur de cette pyramide est multipliée par la demi-base (c'est-à-dire que la pente de la face est ); le carré de la hauteur est égal à l'aire d'une face multipliée par le carré de la demi-base. Le triangle rectangle médian de cette pyramide "dorée" (voir schéma), avec des côtés est intéressant en soi, démontrant via le théorème de Pythagore la relation ou Ce triangle de Kepler est le seul triangle rectangle de proportion avec des longueurs d'arêtes en progression géométrique , tout comme le triangle est la seule proportion de triangle rectangle avec des longueurs d'arête en progression arithmétique . L'angle avec la tangente correspond à l'angle que fait le côté de la pyramide par rapport au sol, ( ).${\displaystyle\varphi }$${\displaystyle {\sqrt {\varphi}}}$${\displaystyle {\sqrt {\varphi}}}$${\displaystyle\varphi }$${\displaystyle 1\mathbin {:} {\sqrt {\varphi }}\mathbin {:} \varphi }$${\textstyle {\sqrt {\varphi }}={\sqrt {\varphi ^{2}-1}}}$${\displaystyle \varphi ={\sqrt {1+\varphi}}.}$${\displaystyle 3\mathbin {:} 4\mathbin {:} 5}$ ${\displaystyle {\sqrt {\varphi}}}$${\displaystyle 51.827^{\circ }}$ ${\displaystyle 51^{\circ }\;49'\;38''}$

Une forme pyramidale presque similaire, mais avec des proportions rationnelles, est décrite dans le Rhind Mathematical Papyrus (la source d'une grande partie des connaissances modernes des mathématiques égyptiennes antiques ), basée sur le triangle ; la pente de la face correspondant à l'angle avec la tangente est, à deux décimales près, ( ). La hauteur oblique ou apothème est multipliée par la demi-base. Le papyrus Rhind a également un autre problème de pyramide, encore une fois avec une pente rationnelle (exprimée en dépassement d'élévation). Les mathématiques égyptiennes n'incluaient pas la notion de nombres irrationnels, et la pente inverse rationnelle (course / montée, multipliée par un facteur de pour convertir en leurs unités conventionnelles de palmiers par coudée) était utilisée dans la construction des pyramides. ${\displaystyle 3\mathbin {:} 4\mathbin {:} 5}$${\displaystyle 4/3}$${\displaystyle 53.13^{\circ }}$ ${\displaystyle 53^{\circ }\;8'}$${\displaystyle 5/3=1.666\ldots}$${\displaystyle 7}$

Des pyramides égyptiennes très proches en proportion de ces pyramides mathématiques sont connues.

Pyramides égyptiennes

La Grande Pyramide de Gizeh

Une pyramide égyptienne proche d'une "pyramide dorée" est la Grande Pyramide de Gizeh (également connue sous le nom de Pyramide de Khéops ou Khufu). Sa pente est proche de l'inclinaison de la pyramide "dorée" de - et encore plus proche de l' inclinaison de la pyramide basée sur - Cependant, plusieurs autres théories mathématiques de la forme de la grande pyramide, basées sur des pentes rationnelles, se sont avérées à la fois plus explications précises et plus plausibles de la pente. ${\displaystyle 51^{\circ }\;52'}$${\displaystyle 51^{\circ }\;50'}$${\style d'affichage \pi}$${\displaystyle 51^{\circ }\;51'.}$${\displaystyle 51^{\circ }\;52'}$

Au milieu du XIXe siècle, Friedrich Röber a étudié diverses pyramides égyptiennes, notamment celles de Khafre , Menkaure et certains des groupes de Gizeh , Saqqarah et Abusir . Il n'a pas appliqué le nombre d'or à la Grande Pyramide de Gizeh, mais a plutôt convenu avec John Shae Perring que son rapport hauteur/côté est Pour toutes les autres pyramides, il a appliqué des mesures liées au triangle de Kepler, et a affirmé que soit leur ensemble ou les longueurs des demi-côtés sont liées à leurs hauteurs par le nombre d'or. ${\displaystyle 8\mathbin {:} 5.}$

En 1859, le pyramidologue John Taylor a mal interprété Hérodote ( vers 440 avant JC ) comme indiquant que la hauteur de la Grande Pyramide au carré est égale à l'aire de l'un de ses triangles faciaux. Cela a conduit Taylor à affirmer que, dans la Grande Pyramide, le nombre d'or est représenté par le rapport de la longueur de la face (la hauteur de la pente, inclinée à un angle par rapport au sol) à la moitié de la longueur du côté de la base carrée (équivalent à la sécante de l'angle ). Les deux longueurs ci-dessus sont d'environ 186,4 mètres (612 pieds) et 115,2 mètres (378 pieds), respectivement. Le rapport de ces longueurs est le nombre d'or, précis à plus de chiffres que l'une ou l'autre des mesures d'origine. De même, Howard Vyse a rapporté la hauteur de la grande pyramide de 148,2 mètres (486 pieds) et la demi-base de 116,4 mètres (382 pieds), ce qui donne le rapport de la hauteur oblique à la demi-base, encore une fois plus précis que la variabilité des données. ${\displaystyle \thêta}$${\displaystyle \thêta}$${\displaystyle 1.6189}$

Eric Temple Bell , mathématicien et historien, a affirmé en 1950 que les mathématiques égyptiennes n'auraient pas permis de calculer la hauteur oblique des pyramides, ou le rapport à la hauteur, sauf dans le cas de la pyramide, puisque le triangle était le seul triangle rectangle connu des Égyptiens et ils ne connaissaient pas le théorème de Pythagore, ni aucun moyen de raisonner sur les irrationnels tels que ou Exemple les problèmes géométriques de conception des pyramides dans le papyrus Rhind correspondent à diverses pentes rationnelles. ${\displaystyle 3\mathbin {:} 4\mathbin {:} 5}$${\displaystyle 3\mathbin {:} 4\mathbin {:} 5}$${\style d'affichage \pi}$${\displaystyle\varphi .}$

Michael Rice affirme que les principales autorités sur l'histoire de l'architecture égyptienne ont soutenu que les Égyptiens connaissaient bien le nombre d'or et qu'il fait partie des mathématiques des pyramides, citant Giedon (1957). Les historiens des sciences ont longtemps débattu de la question de savoir si les Égyptiens possédaient une telle connaissance, affirmant que son apparition dans la Grande Pyramide est le résultat du hasard.

Observations contestées

Voici des exemples d'observations contestées du nombre d'or :

On prétend souvent à tort que les coquilles de nautile sont aux proportions dorées.

• Certaines proportions spécifiques dans le corps de nombreux animaux (y compris les humains) et des parties de coquilles de mollusques sont souvent prétendues être dans le nombre d'or. Cependant, il existe une grande variation dans les mesures réelles de ces éléments chez des individus spécifiques, et la proportion en question est souvent significativement différente du nombre d'or. On a dit que le rapport des os phalangiens successifs des doigts et de l'os métacarpien se rapprochait du nombre d'or. La coquille de nautile , dont la construction se déroule selon une spirale logarithmique , est souvent citée, généralement avec l'idée que toute spirale logarithmique est liée au nombre d'or, mais parfois avec l'affirmation que chaque nouvelle chambre est proportionnée en or par rapport à la précédente. une. Cependant, les mesures des coquilles de nautile ne corroborent pas cette affirmation.
• L'historien John Man déclare que les pages et la zone de texte de la Bible de Gutenberg étaient "basées sur la forme de la section dorée". Cependant, selon ses propres mesures, le rapport hauteur/largeur des pages est${\displaystyle 1.45.}$
• Des études de psychologues, à commencer par Gustav Fechner c. 1876, ont été conçues pour tester l'idée que le nombre d'or joue un rôle dans la perception humaine de la beauté . Alors que Fechner a trouvé une préférence pour les ratios rectangulaires centrés sur le nombre d'or, les tentatives ultérieures pour tester soigneusement une telle hypothèse ont été, au mieux, peu concluantes.
• En investissement, certains praticiens de l'analyse technique utilisent le nombre d'or pour indiquer le soutien d'un niveau de prix, ou la résistance aux hausses de prix, d'une action ou d'une marchandise; après d'importants changements de prix à la hausse ou à la baisse, de nouveaux niveaux de support et de résistance sont censés être trouvés à ou près des prix liés au prix de départ via le nombre d'or. L'utilisation du nombre d'or dans l'investissement est également liée à des schémas plus compliqués décrits par les nombres de Fibonacci (par exemple , le principe d'onde d'Elliott et le retracement de Fibonacci ). Cependant, d'autres analystes du marché ont publié des analyses suggérant que ces pourcentages et modèles ne sont pas étayés par les données.

Le Parthénon

On prétend que de nombreuses proportions du Parthénon présentent le nombre d'or, mais cela a été largement discrédité.

La façade du Parthénon (vers 432 av. J.-C.) ainsi que des éléments de sa façade et d'ailleurs sont, selon certains, circonscrits par des rectangles dorés. D'autres érudits nient que les Grecs aient eu une association esthétique avec le nombre d'or. Par exemple, Keith Devlin dit : « Certes, l'affirmation souvent répétée selon laquelle le Parthénon d'Athènes est basé sur le nombre d'or n'est pas étayée par des mesures réelles. En fait, toute l'histoire sur les Grecs et le nombre d'or semble être sans fondement. " Midhat J. Gazalé affirme que "Ce n'est qu'en Euclide ... que les propriétés mathématiques du nombre d'or ont été étudiées."

À partir des mesures de 15 temples, 18 tombes monumentales, 8 sarcophages et 58 stèles funéraires du cinquième siècle avant JC au deuxième siècle après JC, un chercheur a conclu que le nombre d'or était totalement absent de l'architecture grecque du cinquième siècle classique avant JC, et presque absent pendant les six siècles suivants. Des sources ultérieures comme Vitruve (1er siècle av. J.-C.) discutent exclusivement des proportions qui peuvent être exprimées en nombres entiers, c'est-à-dire proportionnées par opposition aux proportions irrationnelles.

Art moderne

Albert Gleizes , Les Baigneuses (1912)

La Section d'Or ('Golden Section') était un collectif de peintres , sculpteurs, poètes et critiques associés au cubisme et à l'orphisme . Actifs de 1911 à 1914 environ, ils adoptent le nom à la fois pour souligner que le cubisme représente la continuation d'une grande tradition, plutôt que d'être un mouvement isolé, et en hommage à l'harmonie mathématique associée à Georges Seurat . Les cubistes observaient dans ses harmonies, la structuration géométrique du mouvement et de la forme, la primauté de l'idée sur la nature, une clarté scientifique absolue de la conception. Cependant, malgré cet intérêt général pour l'harmonie mathématique, il est plus difficile de déterminer si les peintures présentées dans la célèbre exposition du Salon de la Section d'Or de 1912 utilisaient le nombre d'or dans des compositions. Livio, par exemple, prétend que non, et Marcel Duchamp l'a dit dans une interview. D'autre part, une analyse suggère que Juan Gris a utilisé le nombre d'or dans la composition d'œuvres qui ont été vraisemblablement, mais pas définitivement, présentées à l'exposition. L'historien de l'art Daniel Robbins a fait valoir qu'en plus de faire référence au terme mathématique, le nom de l'exposition fait également référence au groupe antérieur des Bandeaux d'Or , avec lequel Albert Gleizes et d'autres anciens membres de l' Abbaye de Créteil avaient été impliqués.

Piet Mondrian aurait largement utilisé la section dorée dans ses peintures géométriques, bien que d'autres experts (dont le critique Yve-Alain Bois ) aient discrédité ces affirmations.

Voir également

Les références

Notes de bas de page explicatives

Citations

Ouvrages cités

• Livio, Mario (2003) [2002]. Le nombre d'or: l'histoire de Phi, le nombre le plus étonnant du monde (première édition commerciale de poche). New York : Livres de Broadway . ISBN 978-0-7679-0816-0.
• Stakhov, Alexey P. ; Olsen, Scott (2009). Les mathématiques de l'harmonie : d'Euclide aux mathématiques et à l'informatique contemporaines . Singapour : édition scientifique mondiale . ISBN 978-981-277-582-5.

Lectures complémentaires

Liens externes

• " Nombre d'or " , Encyclopédie des mathématiques , EMS Press , 2001 [1994]
• "Golden Section" par Michael Schreiber, Wolfram Demonstrations Project , 2007.
• Weisstein, Eric W. " Nombre d'or " . MathWorld .
• Knott, Ron. "Le rapport de la section d'or : Phi" .Informations et activités par un professeur de mathématiques.
• Le pentagramme et le nombre d'or . Green, Thomas M. Mis à jour en juin 2005. Archivé en novembre 2007. Instruction de géométrie avec problèmes à résoudre.
• Le mythe qui ne disparaîtra pas , de Keith Devlin , traitant de multiples allégations sur l'utilisation du nombre d'or dans la culture.
• Fausses spirales dorées collectées par Randall Munroe
• Conférence YouTube sur le problème des souris de Zeno et les spirales logarithmiques