Triangle héronien - Heronian triangle
En géométrie , un triangle héronien est un triangle dont les côtés et l' aire sont tous des nombres entiers . Les triangles héroniens portent le nom de Héros d'Alexandrie . Le terme est parfois appliqué plus largement aux triangles dont les côtés et l'aire sont tous des nombres rationnels , car on peut redimensionner les côtés par un multiple commun pour obtenir un triangle héronien au sens ci-dessus.
Propriétés
Tout triangle rectangle dont les côtés sont un triplet de Pythagore est un triangle héronien, car les côtés d'un tel triangle sont des nombres entiers , et son aire est également un nombre entier, étant la moitié du produit des deux côtés les plus courts du triangle, à dont au moins un doit être pair.
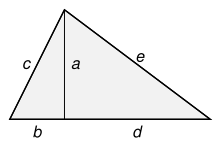
Un exemple de triangle héronien qui n'est pas rectangle est le triangle isocèle de côté 5, 5 et 6, dont l'aire est 12. Ce triangle est obtenu en joignant deux exemplaires du triangle rectangle de côté 3, 4, et 5 le long des côtés de la longueur 4. Cette approche fonctionne en général, comme illustré dans l'image adjacente. On prend un triplet de Pythagore ( a , b , c ), avec c étant le plus grand, puis un autre ( a , d , e ), avec e étant le plus grand, construit les triangles avec ces longueurs latérales, et les joint ensemble le long des côtés de longueur a , pour obtenir un triangle avec des côtés entiers c , e , et b + d , et avec une aire
- (une demi fois la base multipliée par la hauteur).
Si a est pair, l'aire A est un nombre entier. Moins évidemment, si a est impair, alors A est toujours un entier, car b et d doivent tous les deux être pairs, ce qui rend b + d pair également.
Certains triangles héroniens ne peuvent pas être obtenus en joignant deux triangles rectangles à côtés entiers comme décrit ci-dessus. Par exemple, un triangle héronien 5, 29, 30 d'aire 72 ne peut pas être construit à partir de deux triangles pythagoriciens entiers car aucune de ses altitudes n'est entière . De plus, aucun triangle pythagoricien primitif ne peut être construit à partir de deux triangles pythagoriciens entiers plus petits. De tels triangles héroniens sont dits indécomposables . Cependant, si l'on autorise les triplets pythagoriciens avec des valeurs rationnelles, pas nécessairement des entiers, alors une décomposition en triangles rectangles avec des côtés rationnels existe toujours, car chaque altitude d'un triangle héronien est rationnelle (puisqu'elle est égale à deux fois l'aire entière divisée par la base entière) . Ainsi, le triangle héronien de côtés 5, 29, 30 peut être construit à partir de triangles pythagoriciens rationnels de côtés 7/5, 24/5, 5 et 143/5, 24/5, 29. Notez qu'un triplet pythagoricien avec des valeurs rationnelles est juste une version mise à l'échelle d'un triplet avec des valeurs entières.
Les autres propriétés des triangles héroniens sont les suivantes :
- Le périmètre d'un triangle héronien est toujours un nombre pair. Ainsi, chaque triangle héronien a un nombre impair de côtés de longueur paire, et chaque triangle héronien primitif a exactement un côté pair.
- Le demi-périmètre s d'un triangle héronien de côtés a , b et c ne peut jamais être premier. Cela peut être vu du fait que s(s−a)(s−b)(s−c) doit être un carré parfait et si s est un nombre premier alors l'un des autres termes doit avoir s comme facteur mais ceci est impossible car ces termes sont tous inférieurs à s .
- L'aire d'un triangle héronien est toujours divisible par 6.
- Toutes les altitudes d'un triangle héronien sont rationnelles. Cela peut être vu du fait que l'aire d'un triangle est la moitié d'un côté multiplié par son altitude à partir de ce côté, et un triangle héronien a des côtés et une aire entiers. Certains triangles héroniens ont trois altitudes non entières, par exemple l'aigu (15, 34, 35) d'aire 252 et l'obtus (5, 29, 30) d'aire 72. Tout triangle héronien d'une ou plusieurs altitudes non entières peut être agrandie d'un facteur égal au plus petit commun multiple des dénominateurs des altitudes afin d'obtenir un triangle héronien similaire avec trois altitudes entières.
- Les triangles héroniens qui n'ont pas d'altitude entière ( indécomposables et non pythagoriciens) ont des côtés tous divisibles par des nombres premiers de la forme 4 k +1. Cependant les triangles héroniens décomposables doivent avoir deux côtés qui sont l'hypoténuse des triangles pythagoriciens. Ainsi tous les triangles héroniens qui ne sont pas pythagoriciens ont au moins deux côtés divisibles par des nombres premiers de la forme 4 k +1. Il ne reste que des triangles de Pythagore. Par conséquent, tous les triangles héroniens ont au moins un côté qui est divisible par des nombres premiers de la forme 4 k +1. Enfin si un triangle héronien n'a qu'un côté divisible par des nombres premiers de la forme 4 k +1 il doit être pythagoricien avec le côté comme hypoténuse et l'hypoténuse doit être divisible par 5 .
- Toutes les médiatrices intérieures d'un triangle héronien sont rationnelles : pour tout triangle elles sont données par et où les côtés sont a ≥ b ≥ c et l'aire est A ; dans un triangle héronien, tous les a , b , c et A sont des nombres entiers.
- Il n'y a pas de triangles héroniens équilatéraux.
- Il n'y a pas de triangles héroniens avec une longueur de côté de 1 ou 2.
- Il existe une infinité de triangles héroniens primitifs dont un côté est égal à a à condition que a > 2.
- Il n'y a pas de triangles héroniens dont la longueur des côtés forme une progression géométrique .
- Si deux côtés (mais pas trois) d'un triangle héronien ont un facteur commun, ce facteur doit être la somme de deux carrés.
- Chaque angle d'un triangle héronien a un sinus rationnel. Cela découle de la formule d'aire Aire = (1/2) ab sin C , dans laquelle l'aire et les côtés a et b sont des nombres entiers, et de manière équivalente pour les autres angles.
- Chaque angle d'un triangle héronien a un cosinus rationnel. Cela découle de la loi des cosinus , c 2 = a 2 + b 2 − 2 ab cos C , dans laquelle les côtés a , b et c sont des nombres entiers, et de manière équivalente pour les autres angles.
- Étant donné que tous les triangles héroniens ont tous les sinus et cosinus des angles rationnels, cela implique que chaque angle oblique d'un triangle Héron a une tangente, une cotangente, une sécante et une cosécante rationnelles. De plus, la moitié de chaque angle a une tangente rationnelle car tan C/2 = sin C / (1 + cos C) , et de manière équivalente pour les autres angles.
- Il n'y a pas de triangles héroniens dont les trois angles internes forment une progression arithmétique. C'est parce que tous les triangles plans avec des angles dans une progression arithmétique doivent avoir un angle de 60°, qui n'a pas de sinus rationnel.
- Tout carré inscrit dans un triangle héronien a des côtés rationnels : Pour un triangle général, le carré inscrit sur le côté de longueur a a une longueur où A est l'aire du triangle ; dans un triangle héronien, A et a sont des nombres entiers.
- Chaque triangle héronien a un inradius rationnel (rayon de son cercle inscrit) : Pour un triangle général, l'inradius est le rapport de l'aire à la moitié du périmètre, et les deux sont rationnels dans un triangle héronien.
- Chaque triangle héronien a un circumradius rationnel (le rayon de son cercle circonscrit) : Pour un triangle général, le circumradius est égal à un quart du produit des côtés divisé par l'aire ; dans un triangle héronien, les côtés et l'aire sont des nombres entiers.
- Dans un triangle héronien, la distance du centre de gravité à chaque côté est rationnelle, car pour tous les triangles, cette distance est le rapport de deux fois la surface à trois fois la longueur du côté. Cela peut être généralisé en affirmant que tous les centres associés aux triangles héroniens dont les coordonnées barycentriques sont des rapports rationnels ont une distance rationnelle de chaque côté. Ces centres comprennent le circumcenter , orthocentre , centre de neuf points , le point symmedian , le point Gergonne et le point Nagel .
- Tous les triangles héroniens peuvent être placés sur un réseau avec chaque sommet à un point du réseau.
Formule exacte pour tous les triangles héroniens
Le mathématicien indien Brahmagupta (598-668 après JC) a dérivé la solution paramétrique telle que chaque triangle héronien a des côtés proportionnels à :
pour les entiers m , n et k où :
- .
Le coefficient de proportionnalité est généralement un rationnel p / q où q = gcd ( a, b, c ) réduit le triangle de héron généré à ses primitives et p échelles jusqu'à ce primitive à la taille requise. Par exemple, en prenant m = 36, n = 4 et k = 3 produit un triangle avec a = 5220, b = 900 et c = 5400, qui est similaire au triangle héronien 5, 29, 30 et le facteur de proportionnalité utilisé a p = 1 et q = 180.
L'obstacle à une utilisation informatique de la solution paramétrique de Brahmagupta est le dénominateur q du facteur de proportionnalité. q ne peut être déterminé qu'en calculant le plus grand diviseur commun des trois côtés ( pgcd( a, b, c ) ) et introduit un élément d'imprévisibilité dans le processus de génération. Le moyen le plus simple de générer des listes de triangles héroniens est de générer tous les triangles entiers jusqu'à une longueur de côté maximale et de tester une aire intégrale.
Des algorithmes plus rapides ont été dérivés par Kurz (2008) .
Il existe une infinité de triangles héroniens non pythagoriciens primitifs et indécomposables avec des valeurs entières pour l' inradius et les trois exradii , y compris ceux générés par
Il existe une infinité de triangles héroniens qui peuvent être placés sur un réseau de telle sorte que non seulement les sommets se trouvent aux points du réseau, comme c'est le cas pour tous les triangles héroniens, mais en plus les centres du cercle inscrit et des cercles externes se trouvent aux points du réseau.
Voir aussi les formules pour les triangles héroniens avec un angle égal à deux fois l'autre , les triangles héroniens avec des côtés en progression arithmétique , et les triangles héroniens isocèles .
Tous les triangles héroniens à partir de tangentes demi-angles
La tangente de la moitié de tout angle intérieur d'un triangle héronien est nécessairement rationnelle ; voir les propriétés ci-dessus. Ces demi - angles sont positifs, et ils additionnent à 90 ° ( π / 2 radians) du fait que les angles intérieurs ( A , B , C ) de la somme de triangle à 180 ° ( π radians). Nous commençons par choisir r = tan( A /2) et s = tan( B /2) pour être des nombres rationnels positifs satisfaisant rs < 1 . La limite de 1 assure que l'angle A /2 + B /2 est inférieur à 90° et donc que l'angle C /2 sera positif. La valeur t = tan( C /2) sera également un nombre rationnel positif car
Nous pouvons calculer le sinus de n'importe quel angle en utilisant la formule , donc les sinus de sont respectivement. Ces valeurs sont rationnelles car les valeurs de r , s et t sont rationnelles.
Nous utilisons la loi des sinus pour conclure que les longueurs des côtés du triangle sont proportionnelles à ces sinus. Les valeurs entières pour les longueurs des côtés sont obtenues en multipliant les sinus par le plus petit commun multiple de leurs dénominateurs, puis en divisant par le plus grand facteur commun des résultats. Ainsi, nous avons calculé les longueurs des côtés d'un triangle héronien primitif à partir de ses demi-angles tangentes.
Quand c'est aussi le cas que r , s , ou t est égal à 1 alors l'angle intérieur correspondant sera un angle droit et les trois côtés définiront également un triplet de Pythagore .
Exemples
La liste des triangles héroniens entiers primitifs, triés par aire et, si c'est le même, par périmètre , commence comme dans le tableau suivant. « Primitif » signifie que le plus grand diviseur commun des trois longueurs de côté est égal à 1.
| Zone | Périmètre | longueur de côté b+d | longueur de côté e | longueur de côté c |
|---|---|---|---|---|
| 6 | 12 | 5 | 4 | 3 |
| 12 | 16 | 6 | 5 | 5 |
| 12 | 18 | 8 | 5 | 5 |
| 24 | 32 | 15 | 13 | 4 |
| 30 | 30 | 13 | 12 | 5 |
| 36 | 36 | 17 | dix | 9 |
| 36 | 54 | 26 | 25 | 3 |
| 42 | 42 | 20 | 15 | 7 |
| 60 | 36 | 13 | 13 | dix |
| 60 | 40 | 17 | 15 | 8 |
| 60 | 50 | 24 | 13 | 13 |
| 60 | 60 | 29 | 25 | 6 |
| 66 | 44 | 20 | 13 | 11 |
| 72 | 64 | 30 | 29 | 5 |
| 84 | 42 | 15 | 14 | 13 |
| 84 | 48 | 21 | 17 | dix |
| 84 | 56 | 25 | 24 | 7 |
| 84 | 72 | 35 | 29 | 8 |
| 90 | 54 | 25 | 17 | 12 |
| 90 | 108 | 53 | 51 | 4 |
| 114 | 76 | 37 | 20 | 19 |
| 120 | 50 | 17 | 17 | 16 |
| 120 | 64 | 30 | 17 | 17 |
| 120 | 80 | 39 | 25 | 16 |
| 126 | 54 | 21 | 20 | 13 |
| 126 | 84 | 41 | 28 | 15 |
| 126 | 108 | 52 | 51 | 5 |
| 132 | 66 | 30 | 25 | 11 |
| 156 | 78 | 37 | 26 | 15 |
| 156 | 104 | 51 | 40 | 13 |
| 168 | 64 | 25 | 25 | 14 |
| 168 | 84 | 39 | 35 | dix |
| 168 | 98 | 48 | 25 | 25 |
| 180 | 80 | 37 | 30 | 13 |
| 180 | 90 | 41 | 40 | 9 |
| 198 | 132 | 65 | 55 | 12 |
| 204 | 68 | 26 | 25 | 17 |
| 210 | 70 | 29 | 21 | 20 |
| 210 | 70 | 28 | 25 | 17 |
| 210 | 84 | 39 | 28 | 17 |
| 210 | 84 | 37 | 35 | 12 |
| 210 | 140 | 68 | 65 | 7 |
| 210 | 300 | 149 | 148 | 3 |
| 216 | 162 | 80 | 73 | 9 |
| 234 | 108 | 52 | 41 | 15 |
| 240 | 90 | 40 | 37 | 13 |
| 252 | 84 | 35 | 34 | 15 |
| 252 | 98 | 45 | 40 | 13 |
| 252 | 144 | 70 | 65 | 9 |
| 264 | 96 | 44 | 37 | 15 |
| 264 | 132 | 65 | 34 | 33 |
| 270 | 108 | 52 | 29 | 27 |
| 288 | 162 | 80 | 65 | 17 |
| 300 | 150 | 74 | 51 | 25 |
| 300 | 250 | 123 | 122 | 5 |
| 306 | 108 | 51 | 37 | 20 |
| 330 | 100 | 44 | 39 | 17 |
| 330 | 110 | 52 | 33 | 25 |
| 330 | 132 | 61 | 60 | 11 |
| 330 | 220 | 109 | 100 | 11 |
| 336 | 98 | 41 | 40 | 17 |
| 336 | 112 | 53 | 35 | 24 |
| 336 | 128 | 61 | 52 | 15 |
| 336 | 392 | 195 | 193 | 4 |
| 360 | 90 | 36 | 29 | 25 |
| 360 | 100 | 41 | 41 | 18 |
| 360 | 162 | 80 | 41 | 41 |
| 390 | 156 | 75 | 68 | 13 |
| 396 | 176 | 87 | 55 | 34 |
| 396 | 198 | 97 | 90 | 11 |
| 396 | 242 | 120 | 109 | 13 |
Les listes des triangles héroniens primitifs dont les côtés ne dépassent pas 6 000 000 peuvent être trouvées dans "Listes des triangles héroniens primitifs" . Sascha Kurz, Université de Bayreuth, Allemagne. Archivé (PDF) à partir de l'original en mai 2016 . Consulté le 29 mars 2016 .
Triangles égaux
Une forme est dite égale si son aire est égale à son périmètre. Il y a exactement cinq triangles héroniens égaux : ceux avec des longueurs de côté (5,12,13), (6,8,10), (6,25,29), (7,15,20) et (9,10 ,17).
Triangles héroniens presque équilatéraux
Puisque l'aire d'un triangle équilatéral à côtés rationnels est un nombre irrationnel , aucun triangle équilatéral n'est héronien. Cependant, il existe une séquence unique de triangles héroniens qui sont "presque équilatéraux" car les trois côtés sont de la forme n − 1, n , n + 1. Une méthode pour générer toutes les solutions à ce problème basée sur des fractions continues a été décrite dans 1864 par Edward Sang , et en 1880 Reinhold Hoppe a donné une expression fermée pour les solutions. Les premiers exemples de ces triangles presque équilatéraux sont répertoriés dans le tableau suivant (séquence A003500 dans l' OEIS ) :
| Longueur du côté | Zone | rayon d'action | ||
|---|---|---|---|---|
| n − 1 | m | n +1 | ||
| 3 | 4 | 5 | 6 | 1 |
| 13 | 14 | 15 | 84 | 4 |
| 51 | 52 | 53 | 1170 | 15 |
| 193 | 194 | 195 | 16296 | 56 |
| 723 | 724 | 725 | 226974 | 209 |
| 2701 | 2702 | 2703 | 3161340 | 780 |
| 10083 | 10084 | 10085 | 44031786 | 2911 |
| 37633 | 37634 | 37635 | 613283664 | 10864 |
Les valeurs suivantes de n peuvent être trouvées en multipliant la valeur précédente par 4, puis en soustrayant la valeur avant celle-ci (52 = 4 × 14 − 4, 194 = 4 × 52 − 14, etc.), ainsi :
où t désigne n'importe quelle ligne du tableau. C'est une séquence de Lucas . Alternativement, la formule génère tous les n . De manière équivalente, soit A = aire et y = rayon infra, alors,
où { n , y } sont des solutions de n 2 − 12 y 2 = 4. Une petite transformation n = 2x donne une équation de Pell conventionnelle x 2 − 3 y 2 = 1, dont les solutions peuvent alors être dérivées de la suite régulière expansion fractionnaire pour √ 3 .
La variable n est de la forme , où k vaut 7, 97, 1351, 18817, …. Les nombres de cette séquence ont la propriété que k entiers consécutifs ont un écart type intégral .
Voir également
- tétraèdre héronien
- quadrilatère de Brahmagupta
- Pentagone de Robbins
- Triangle entier#Triangles héroniens
Les références
Liens externes
- Weisstein, Eric W. "Triangle héronien" . MathWorld .
- Encyclopédie en ligne des séquences entières Heronian
- Wm. Fitch Cheney, Jr. (janvier 1929), "Triangles héroniennes", Amer. Math. Mensuel , 36 (1) : 22–28, doi : 10.1080/00029890.1929.11986902 , JSTOR 2300173
- S. sh. Kozhegel'dinov (1994), "Sur les triangles héroniens fondamentaux", Math. Notes , 55 (2) : 151–6, doi : 10.1007/BF02113294 , S2CID 115233024