Triangle isocèle - Isosceles triangle

Triangle isocèle
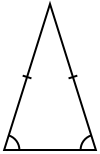Triangle isocèle à axe de symétrie vertical
Taper	Triangle
Arêtes et sommets	3
Symbole Schläfli	( ) { }
Groupe Symétrie	Dih 2 , [ ], (*), ordre 2
Double polygone	Auto-dual
Propriétés	convexe , cyclique

En géométrie , un triangle isocèle est un triangle qui a deux côtés de même longueur. Parfois, il est spécifié comme ayant exactement deux côtés de même longueur, et parfois comme ayant au moins deux côtés de même longueur, cette dernière version incluant ainsi le triangle équilatéral comme cas particulier . Des exemples de triangles isocèles comprennent le triangle rectangle isocèle , le triangle d'or et les faces des bipyramides et certains solides catalans .

L'étude mathématique des triangles isocèles remonte aux mathématiques égyptiennes antiques et aux mathématiques babyloniennes . Les triangles isocèles ont été utilisés comme décoration depuis des temps encore plus anciens et apparaissent fréquemment dans l'architecture et le design, par exemple dans les frontons et les pignons des bâtiments.

Les deux côtés égaux sont appelés les jambes et le troisième côté est appelé la base du triangle. Les autres dimensions du triangle, telles que sa hauteur, sa superficie et son périmètre, peuvent être calculées par des formules simples à partir des longueurs des pattes et de la base. Tout triangle isocèle a un axe de symétrie le long de la médiatrice de sa base. Les deux angles opposés aux jambes sont égaux et sont toujours aigus , de sorte que la classification du triangle comme aigu, droit ou obtus ne dépend que de l'angle entre ses deux jambes.

Terminologie, classification et exemples

Euclide a défini un triangle isocèle comme un triangle avec exactement deux côtés égaux, mais les traitements modernes préfèrent définir les triangles isocèles comme ayant au moins deux côtés égaux. La différence entre ces deux définitions est que la version moderne fait des triangles équilatéraux (avec trois côtés égaux) un cas particulier des triangles isocèles. Un triangle qui n'est pas isocèle (ayant trois côtés inégaux) est appelé scalène . "Isocèle" est fabriqué à partir des racines grecques "isos" (égal) et "skelos" (jambe). Le même mot est utilisé, par exemple, pour les trapèzes isocèles , les trapèzes à deux côtés égaux, et pour les ensembles isocèles , ensembles de points tous les trois formant un triangle isocèle.

Dans un triangle isocèle qui a exactement deux côtés égaux, les côtés égaux sont appelés jambes et le troisième côté est appelé base . L'angle inclus par les jambes est appelé l' angle au sommet et les angles qui ont la base comme l'un de leurs côtés sont appelés les angles de base . Le sommet opposé à la base s'appelle le sommet . Dans le cas du triangle équilatéral, puisque tous les côtés sont égaux, n'importe quel côté peut être appelé la base.

Triangles isocèles spéciaux

Triangle rectangle isocèle

Trois carrés inscrits congruents dans le triangle de Calabi

Un triangle d'or subdivisé en un triangle d'or plus petit et un gnomon d'or

Le carrelage triangulaire triakis

Solides catalans à faces triangulaires isocèles

Tétraèdre de Triakis

Octaèdre de Triakis

Hexaèdre Tetrakis

dodécaèdre de pentakis

Icosaèdre de Triakis

Qu'un triangle isocèle soit aigu, droit ou obtus ne dépend que de l'angle à son sommet. En géométrie euclidienne , les angles de base ne peuvent pas être obtus (supérieurs à 90°) ou droits (égal à 90°) car leurs mesures totaliseraient au moins 180°, le total de tous les angles d'un triangle euclidien. Puisqu'un triangle est obtus ou droit si et seulement si l'un de ses angles est respectivement obtus ou droit, un triangle isocèle est obtus, droit ou aigu si et seulement si son angle au sommet est respectivement obtus, droit ou aigu. Dans le livre d' Edwin Abbott Flatland , cette classification des formes était utilisée comme une satire de la hiérarchie sociale : les triangles isocèles représentaient la classe ouvrière , avec des triangles isocèles aigus plus haut dans la hiérarchie que les triangles isocèles rectangles ou obtus.

En plus du triangle rectangle isocèle , plusieurs autres formes spécifiques de triangles isocèles ont été étudiées. Ceux-ci incluent le triangle de Calabi (un triangle avec trois carrés inscrits congrus), le triangle d'or et le gnomon d'or (deux triangles isocèles dont les côtés et la base sont dans le nombre d' or ), le triangle 80-80-20 apparaissant dans le puzzle Angles adventifs de Langley , et le triangle 30-30-120 du carrelage triangulaire triakis . Cinq solides catalans , le triakitétraèdre , triakioctaèdre , tétrakihexaèdre , pentakidodécaèdre et Triakis icosaèdre , ont chacun visages isocèle triangle, tout comme une infinité de pyramides et bipyramides .

Formules

Hauteur

Pour tout triangle isocèle, les six segments de droite suivants coïncident :

• l' altitude , un segment de droite partant du sommet perpendiculaire à la base,
• la bissectrice du sommet à la base,
• la médiane du sommet au milieu de la base,
• la médiatrice de la base à l'intérieur du triangle,
• le segment à l'intérieur du triangle de l'unique axe de symétrie du triangle, et
• le segment à l'intérieur du triangle de la ligne d'Euler du triangle, sauf lorsque le triangle est équilatéral .

Leur longueur commune est la hauteur du triangle. Si le triangle a des côtés égaux de longueur et de base de longueur , les formules générales du triangle pour les longueurs de ces segments se simplifient toutes en ${\style d'affichage h}$${\style d'affichage a}$${\style d'affichage b}$

${\displaystyle h={\frac {1}{2}}{\sqrt {4a^{2}-b^{2}}}.}$

Cette formule peut également être dérivée du théorème de Pythagore en utilisant le fait que l'altitude coupe la base et divise le triangle isocèle en deux triangles rectangles congrus.

La droite d'Euler de tout triangle passe par l' orthocentre du triangle (l'intersection de ses trois altitudes), son centre de gravité (l'intersection de ses trois médianes) et son centre circonscrit (l'intersection des médiatrices de ses trois côtés, qui est aussi le centre du cercle circonscrit qui passe par les trois sommets). Dans un triangle isocèle avec exactement deux côtés égaux, ces trois points sont distincts, et (par symétrie) se trouvent tous sur l'axe de symétrie du triangle, d'où il suit que la ligne d'Euler coïncide avec l'axe de symétrie. Le centre du triangle se trouve également sur la ligne d'Euler, ce qui n'est pas vrai pour les autres triangles. Si deux d'une bissectrice, d'une médiane ou d'une altitude coïncident dans un triangle donné, ce triangle doit être isocèle.

Zone

L'aire d'un triangle isocèle peut être dérivée de la formule de sa hauteur et de la formule générale de l'aire d'un triangle comme la moitié du produit de la base et de la hauteur : ${\style d'affichage T}$

${\displaystyle T={\frac {b}{4}}{\sqrt {4a^{2}-b^{2}}}.}$

La même formule d'aire peut également être dérivée de la formule de Heron pour l'aire d'un triangle à partir de ses trois côtés. Cependant, l'application directe de la formule de Heron peut être numériquement instable pour les triangles isocèles avec des angles très vifs, en raison de la quasi-annulation entre le demi - périmètre et la longueur des côtés dans ces triangles.

Si l'angle au sommet et la longueur des jambes d'un triangle isocèle sont connus, alors l'aire de ce triangle est : ${\style d'affichage (\theta )}$${\style d'affichage (a)}$

${\displaystyle T={\frac {1}{2}}a^{2}\sin \theta .}$

C'est un cas particulier de la formule générale pour l'aire d'un triangle comme la moitié du produit de deux côtés par le sinus de l'angle inclus.

Périmètre

Le périmètre d'un triangle isocèle de côtés et de base égaux est juste ${\style d'affichage p}$${\style d'affichage a}$${\style d'affichage b}$

${\style d'affichage p=2a+b.}$

Comme dans tout triangle, l'aire et le périmètre sont liés par l' inégalité isopérimétrique${\style d'affichage T}$${\style d'affichage p}$

${\displaystyle p^{2}>12{\sqrt {3}}T.}$

C'est une inégalité stricte pour les triangles isocèles avec des côtés différents de la base, et devient une égalité pour le triangle équilatéral. L'aire, le périmètre et la base peuvent également être liés les uns aux autres par l'équation

${\displaystyle 2pb^{3}-p^{2}b^{2}+16T^{2}=0.}$

Si la base et le périmètre sont fixes, cette formule détermine l'aire du triangle isocèle résultant, qui est le maximum possible parmi tous les triangles ayant la même base et le même périmètre. En revanche, si l'aire et le périmètre sont fixes, cette formule permet de récupérer la longueur de base, mais pas uniquement : il y a en général deux triangles isocèles distincts d'aire et de périmètre donnés . Lorsque l'inégalité isopérimétrique devient une égalité, il n'y a qu'un seul tel triangle, qui est équilatéral. ${\style d'affichage T}$${\style d'affichage p}$

Longueur de la bissectrice

Si les deux côtés égaux ont une longueur et l'autre côté a une longueur , alors la bissectrice de l' angle interne de l'un des deux sommets d'angle égal satisfait ${\style d'affichage a}$${\style d'affichage b}$ ${\style d'affichage t}$

${\displaystyle {\frac {2}ab}{a+b}}>t>{\frac {ab{\sqrt {2}}}{a+b}}}$

aussi bien que

${\style d'affichage t<{\frac {4a}{3}} ;}$

et inversement, si cette dernière condition est vérifiée, un triangle isocèle paramétré par et existe. ${\style d'affichage a}$${\style d'affichage t}$

Le théorème de Steiner-Lehmus stipule que tout triangle avec deux bissectrices de longueurs égales est isocèle. Il a été formulé en 1840 par CL Lehmus . Son autre homonyme, Jakob Steiner , a été l'un des premiers à apporter une solution. Bien que formulé à l'origine uniquement pour les bissectrices d'angle internes, il fonctionne dans de nombreux cas (mais pas dans tous) lorsque, à la place, deux bissectrices d'angle externes sont égales. Le triangle isocèle 30-30-120 constitue un cas limite pour cette variation du théorème, car il a quatre bissectrices d'angle égal (deux internes, deux externes).

Rayons

Triangle isocèle montrant son centre circonscrit (bleu), son centre de gravité (rouge), son centre (vert) et son axe de symétrie (violet)

Les formules inradius et circumradius pour un triangle isocèle peuvent être dérivées de leurs formules pour des triangles arbitraires. Le rayon du cercle inscrit d'un triangle isocèle de longueur de côté , de base et de hauteur est : ${\style d'affichage a}$${\style d'affichage b}$${\style d'affichage h}$

${\displaystyle {\frac {2ab-b^{2}}{4h}}.}$

Le centre du cercle se trouve sur l'axe de symétrie du triangle, cette distance au-dessus de la base. Un triangle isocèle a le plus grand cercle inscrit possible parmi les triangles ayant la même base et le même angle au sommet, ainsi que la plus grande aire et le plus grand périmètre parmi la même classe de triangles.

Le rayon du cercle circonscrit est :

${\displaystyle {\frac {a^{2}}{2h}}.}$

Le centre du cercle se trouve sur l'axe de symétrie du triangle, cette distance en dessous du sommet.

Carré inscrit

Pour tout triangle isocèle, il existe un carré unique avec un côté colinéaire avec la base du triangle et les deux coins opposés de ses côtés. Le triangle de Calabi est un triangle isocèle spécial avec la propriété que les deux autres carrés inscrits, avec des côtés colinéaires avec les côtés du triangle, sont de la même taille que le carré de base. Un théorème beaucoup plus ancien, conservé dans les travaux de Héros d'Alexandrie , stipule que, pour un triangle isocèle de base et de hauteur , la longueur du côté du carré inscrit sur la base du triangle est ${\style d'affichage b}$${\style d'affichage h}$

${\style d'affichage {\frac {bh}{b+h}}.}$

Subdivision isocèle d'autres formes

Partage d'un pentagone cyclique en triangles isocèles par les rayons de son cercle circonscrit

Pour tout entier , tout triangle peut être partitionné en triangles isocèles. Dans un triangle rectangle , la médiane de l'hypoténuse (c'est-à-dire le segment de droite allant du milieu de l'hypoténuse au sommet à angle droit) divise le triangle rectangle en deux triangles isocèles. En effet, le milieu de l'hypoténuse est le centre du cercle circonscrit du triangle rectangle et chacun des deux triangles créés par la partition a deux rayons égaux comme deux de ses côtés. De même, un triangle aigu peut être divisé en trois triangles isocèles par segments à partir de son centre circonscrit, mais cette méthode ne fonctionne pas pour les triangles obtus, car le centre circonscrit se trouve à l'extérieur du triangle. ${\style d'affichage n\geq 4}$${\style d'affichage n}$

En généralisant la partition d'un triangle aigu, tout polygone cyclique qui contient le centre de son cercle circonscrit peut être partitionné en triangles isocèles par les rayons de ce cercle passant par ses sommets. Le fait que tous les rayons d'un cercle aient la même longueur implique que tous ces triangles sont isocèles. Cette partition peut être utilisée pour dériver une formule pour l'aire du polygone en fonction de ses longueurs de côté, même pour les polygones cycliques qui ne contiennent pas leurs centres circonscrits. Cette formule généralise la formule de Heron pour les triangles et la formule de Brahmagupta pour les quadrilatères cycliques .

L' une ou l'autre diagonale d'un losange le divise en deux triangles isocèles congruents . De même, l'une des deux diagonales d'un cerf - volant le divise en deux triangles isocèles, qui ne sont congrus que lorsque le cerf-volant est un losange.

Applications

En architecture et design

Fronton obtus isocèle du Panthéon, Rome

Pignon isocèle aigu sur le portail Saint-Etienne, Notre-Dame de Paris

Les triangles isocèles apparaissent généralement en architecture sous la forme de pignons et de frontons . Dans l'architecture grecque antique et ses imitations ultérieures, le triangle isocèle obtus était utilisé; dans l'architecture gothique, il a été remplacé par le triangle aigu isocèle.

Dans l' architecture du Moyen Âge , une autre forme de triangle isocèle est devenue populaire : le triangle isocèle égyptien. C'est un triangle isocèle qui est aigu, mais moins que le triangle équilatéral ; sa hauteur est proportionnelle aux 5/8 de sa base. Le triangle isocèle égyptien a été remis en usage dans l'architecture moderne par l'architecte néerlandais Hendrik Petrus Berlage .

Vue détaillée d'un treillis Warren modifié avec des verticales

Les structures en treillis Warren , telles que les ponts, sont généralement disposées en triangles isocèles, bien que parfois des poutres verticales soient également incluses pour une résistance supplémentaire. Les surfaces tesselées par des triangles isocèles obtus peuvent être utilisées pour former des structures déployables qui ont deux états stables : un état déplié dans lequel la surface s'étend en une colonne cylindrique et un état plié dans lequel elle se replie en une forme de prisme plus compacte qui peut être plus facilement transportable. Le même motif de tessellation forme la base du flambement de Yoshimura , un motif formé lorsque des surfaces cylindriques sont comprimées axialement, et de la lanterne de Schwarz , un exemple utilisé en mathématiques pour montrer que l'aire d'une surface lisse ne peut pas toujours être approchée avec précision par des polyèdres convergeant vers la surface.

Drapeau de la Guyane

Drapeau de Sainte-Lucie

Dans le graphisme et les arts décoratifs , les triangles isocèles ont été un élément de conception fréquent dans les cultures du monde entier, depuis au moins le Néolithique ancien jusqu'aux temps modernes. Ils sont un élément de conception commun dans les drapeaux et l' héraldique , apparaissant en évidence avec une base verticale, par exemple, dans le drapeau de la Guyane , ou avec une base horizontale dans le drapeau de Sainte-Lucie , où ils forment une image stylisée d'une île de montagne.

Ils ont également été utilisés dans des conceptions ayant une signification religieuse ou mystique, par exemple dans le Sri Yantra de la pratique de la méditation hindoue .

Dans d'autres domaines des mathématiques

Si une équation cubique à coefficients réels a trois racines qui ne sont pas toutes des nombres réels , alors lorsque ces racines sont tracées dans le plan complexe sous forme de diagramme d'Argand, elles forment les sommets d'un triangle isocèle dont l'axe de symétrie coïncide avec l'axe horizontal (réel) . En effet, les racines complexes sont des conjugués complexes et sont donc symétriques par rapport à l'axe réel.

En mécanique céleste , le problème des trois corps a été étudié dans le cas particulier où les trois corps forment un triangle isocèle, car supposer que les corps sont disposés de cette manière réduit le nombre de degrés de liberté du système sans le réduire au Cas ponctuel lagrangien résolu lorsque les corps forment un triangle équilatéral. Les premiers exemples du problème à trois corps dont les oscillations sont illimitées se trouvent dans le problème à trois corps isocèle.

Histoire et illusions

Bien avant que les triangles isocèles ne soient étudiés par les anciens mathématiciens grecs , les praticiens des mathématiques égyptiennes antiques et des mathématiques babyloniennes savaient comment calculer leur aire. Des problèmes de ce type sont inclus dans le papyrus mathématique de Moscou et le papyrus mathématique de Rhind .

Le théorème selon lequel les angles à la base d'un triangle isocèle sont égaux apparaît comme la proposition I.5 dans Euclide. Ce résultat a été appelé le pons asinorum (le pont des ânes) ou le théorème du triangle isocèle. Les explications rivales de ce nom incluent la théorie selon laquelle c'est parce que le diagramme utilisé par Euclide dans sa démonstration du résultat ressemble à un pont, ou parce que c'est le premier résultat difficile dans Euclide, et agit pour séparer ceux qui peuvent comprendre la géométrie d'Euclide de ceux qui ne peut pas.

Une erreur bien connue est la fausse preuve de l'affirmation selon laquelle tous les triangles sont isocèles . Robin Wilson attribue cet argument à Lewis Carroll , qui l'a publié en 1899, mais WW Rouse Ball l'a publié en 1892 et a écrit plus tard que Carroll a obtenu l'argument de lui. L'erreur est enracinée dans le manque de reconnaissance d'Euclide du concept d'entre- deux et l'ambiguïté qui en résulte entre l' intérieur et l' extérieur des figures.

Remarques

Les références

Liens externes

• Weisstein, Eric W. , "Triangle isocèle" , MathWorld