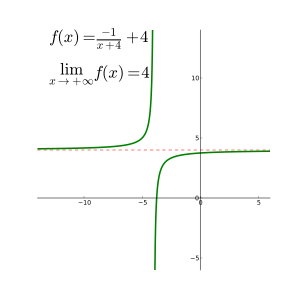
Limite d'une fonction - Limit of a function

Fait partie d'une série d'articles sur
Calcul
Théorème fondamental Règle intégrale de Leibniz Limites des fonctions Continuité Théorème de la valeur moyenne Le théorème de Rolle
Différentiel Définitions Dérivé  ( généralisations ) Différentiel infinitésimal d'une fonction le total notions Notation de différenciation Dérivée seconde Différenciation implicite Différenciation logarithmique Tarifs associés Le théorème de Taylor Règles et identités Somme Produit Chaîne Puissance Quotient La règle de l'Hôpital Inverse Général Leibniz La formule de Faà di Bruno Reynolds
Intégral Listes d'intégrales Transformation intégrale Définitions Primitive Intégral  ( impropre ) intégrale de Riemann Intégration de Lebesgue Intégration des contours Intégrale des fonctions inverses Intégration par les pièces Disques Coquilles cylindriques Substitution  ( trigonométrique , Weierstrass , Euler ) la formule d'Euler Fractions partielles Modification de l'ordre Formules de réduction Différencier sous le signe intégral Algorithme de Risch
Séries Géométrique  ( arithmético-géométrique ) Harmonique en alternance Puissance Binôme Taylor Tests de convergence Limite de sommation (test de terme) Rapport Racine Intégral Comparaison directe Comparaison des limites Série alternée Cauchy condensation Dirichlet Abel
Vecteur Pente Divergence Boucle Laplacien Dérivée directionnelle Identités Théorèmes Pente Légumes verts Stokes' Divergence Stokes généralisé
Multivariable Formalismes Matrice Tenseur Extérieur Géométrique Définitions Dérivée partielle Intégrale multiple Intégrale de ligne Intégrale surfacique Intégrale de volume Jacobien Toile de jute
Spécialisé Fractionnaire Malliavin Stochastique Variantes
Divers Précalcul Histoire Glossaire Liste des sujets Abeille d'intégration Une analyse
v t e

En mathématiques , la limite d'une fonction est un concept fondamental en calcul et en analyse concernant le comportement de cette fonction à proximité d'une entrée particulière .

Les définitions formelles, conçues pour la première fois au début du XIXe siècle, sont données ci-dessous. De manière informelle, une fonction f affecte une sortie f ( x ) à chaque entrée x . On dit que la fonction a une limite L à une entrée p, si f ( x ) se rapproche de plus en plus de L à mesure que x se rapproche de p . Plus précisément, lorsque f est appliqué à toute entrée suffisamment proche de p , la valeur de sortie est forcée arbitrairement proche de L . D'un autre côté, si certaines entrées très proches de p sont amenées à des sorties qui restent à une distance fixe, alors nous disons que la limite n'existe pas .

La notion de limite a de nombreuses applications dans le calcul moderne . En particulier, les nombreuses définitions de la continuité emploient le concept de limite : grosso modo, une fonction est continue si toutes ses limites sont en accord avec les valeurs de la fonction. La notion de limite apparaît aussi dans la définition de la dérivée : dans le calcul d'une variable, c'est la valeur limite de la pente des droites sécantes au graphe d'une fonction.

Histoire

Bien qu'implicite dans le développement du calcul des XVIIe et XVIIIe siècles, l'idée moderne de la limite d'une fonction remonte à Bolzano qui, en 1817, introduisit les bases de la technique epsilon-delta pour définir les fonctions continues. Cependant, son travail n'était pas connu de son vivant.

Dans son livre Cours d'analyse de 1821 , Cauchy a discuté des quantités variables, des infinitésimaux et des limites, et a défini la continuité de en disant qu'un changement infinitésimal de x produit nécessairement un changement infinitésimal de y , tandis que ( Grabiner 1983 ) prétend qu'il a utilisé un epsilon rigoureux -définition delta dans les preuves. Weierstrass a introduit pour la première fois la définition epsilon-delta de la limite sous la forme qu'elle est habituellement écrite aujourd'hui. Il a également introduit les notations lim et lim _{x → x 0} . ${\style d'affichage y=f(x)}$

La notation moderne consistant à placer la flèche sous le symbole de la limite est due à Hardy , qui est introduit dans son livre A Course of Pure Mathematics en 1908.

Motivation

Imaginez une personne marchant sur un paysage représenté par le graphique de y = f ( x ). Leur position horizontale est mesurée par la valeur de x , tout comme la position donnée par une carte du territoire ou par un système de positionnement global . Leur altitude est donnée par la coordonnée y . Ils marchent vers la position horizontale donnée par x = p . Au fur et à mesure qu'ils s'en approchent, ils remarquent que leur altitude se rapproche de L . Si interrogé sur l'altitude de x = p , ils seraient alors répondre à L .

Qu'est-ce que cela veut dire, alors, que leur altitude se rapproche de L ? Cela signifie que leur altitude se rapproche de plus en plus de L, à l' exception d'une éventuelle petite erreur de précision. Par exemple, supposons que nous fixions un objectif de précision particulier pour notre voyageur : il doit s'approcher à moins de dix mètres de L . Ils rapportent qu'en effet, ils peuvent s'approcher à moins de dix mètres verticaux de L , puisqu'ils constatent que lorsqu'ils sont à moins de cinquante mètres horizontaux de p , leur altitude est toujours de dix mètres ou moins de L .

L'objectif de précision est alors modifié : peuvent-ils s'approcher à moins d'un mètre vertical ? Oui. S'ils se trouvent n'importe où à moins de sept mètres horizontaux de p , leur altitude restera toujours à moins d'un mètre de la cible L . En résumé, dire que l'altitude du voyageur se rapproche de L lorsque sa position horizontale se rapproche de p , c'est dire que pour chaque objectif de précision cible, aussi petit soit-il, il existe un voisinage de p dont l'altitude remplit cet objectif de précision.

La déclaration informelle initiale peut maintenant être expliquée :

La limite d'une fonction f ( x ) lorsque x se rapproche de p est un nombre L avec la propriété suivante : étant donné toute distance cible de L , il existe une distance de p à l' intérieur de laquelle les valeurs de f ( x ) restent à l'intérieur de la distance cible.

En fait, cet énoncé explicite est assez proche de la définition formelle de la limite d'une fonction, avec des valeurs dans un espace topologique .

Plus précisément, pour dire que

${\displaystyle \lim _{x\to p}f(x)=L,\,}$

c'est-à-dire que ƒ ( x ) peut être rendu aussi proche de L que souhaité, en rendant x suffisamment proche, mais non égal, de  p .

Les définitions suivantes, connues sous le nom de (ε, )-définitions, sont les définitions généralement acceptées pour la limite d'une fonction dans divers contextes.

Fonctions d'une seule variable

(ε, δ)-définition de la limite

Supposons que f  : R → R est défini sur la ligne réelle et p, L ∈ R . On dirait que la limite de f , lorsque x tend vers p , est L et s'écrit

${\displaystyle \lim _{x\to p}f(x)=L,}$

ou bien comme :

${\style d'affichage f(x)\à L}$comme (lit " tend vers comme tend vers ")${\style d'affichage x\à p}$${\style d'affichage f(x)}$${\style d'affichage L}$${\style d'affichage x}$${\style d'affichage p}$

si la propriété suivante est vérifiée :

• Pour tout réel ε > 0 , il existe un réel δ > 0 tel que pour tout réel x, 0 < | x − p | < δ implique que | f ( x ) − L | < ε .

Une définition plus générale s'applique aux fonctions définies sur des sous - ensembles de la ligne réelle. Soit ( a ,  b ) un intervalle ouvert dans R , et p un point de ( a ,  b ). Soit f une fonction à valeur réelle définie sur l'ensemble de ( a ,  b )—sauf éventuellement en p lui-même. On dit alors que la limite de f lorsque x tend vers p est L, si pour tout réel ε > 0 , il existe un réel δ > 0 tel que 0 < | x − p | < δ et x ∈ ( a , b ) implique que | f ( x ) − L | < ε .

Ici, notez que la valeur de la limite ne dépend pas du fait que f soit défini en p , ni de la valeur f ( p ) - si elle est définie.

Les lettres e et δ peuvent être compris comme « erreur » et « distance ». En fait, Cauchy a utilisé ε comme abréviation d'"erreur" dans certains de ses travaux, bien que dans sa définition de la continuité, il ait utilisé un infinitésimal plutôt que ε ou δ (voir Cours d'Analyse ). Dans ces conditions, l'erreur ( ε ) dans la mesure de la valeur à la limite peut être aussi faible que souhaité, en réduisant la distance ( δ ) jusqu'au point de fin de course. Comme indiqué ci-dessous, cette définition fonctionne également pour les fonctions dans un contexte plus général. L'idée que δ et e représentent des distances aide suggèrent que ces généralisations. ${\style d'affichage \alpha }$

Existence et limites unilatérales

Alternativement, x peut approcher p d'en haut (à droite) ou d'en bas (à gauche), auquel cas les limites peuvent être écrites comme

${\displaystyle \lim _{x\to p^{+}}f(x)=L}$

ou

${\displaystyle \lim _{x\to p^{-}}f(x)=L}$

respectivement. Si ces limites existent à p et y sont égales, alors cela peut être appelé la limite de f ( x ) à p . Si les limites unilatérales existent en p , mais sont inégales, alors il n'y a pas de limite en p (c'est-à-dire que la limite en p n'existe pas). Si l'une des limites unilatérales n'existe pas en p , alors la limite en p n'existe pas non plus.

Une définition formelle est la suivante. La limite de f ( x ) lorsque x tend vers p par le haut est L si, pour tout ε  > 0, il existe a δ > 0 tel que | f ( x ) −  L | <  ε chaque fois que 0 <  x  −  p  <  δ . La limite de f ( x ) comme x approche p en bas est L si, pour tout ε > 0, il existe un δ > 0 tel que | f ( x ) −  L | <  ε chaque fois que 0 <  p  −  x  <  δ .

Si la limite n'existe pas, alors l' oscillation de f en p est non nulle.

Sous-ensembles plus généraux

En dehors des intervalles ouverts, des limites peuvent être définies pour des fonctions sur des sous-ensembles arbitraires de R , comme suit ( Bartle & Sherbert 2000 ) : soit f une fonction à valeur réelle définie sur un sous-ensemble S de la droite réelle. Soit p un point limite de S, c'est-à-dire que p est la limite d'une séquence d'éléments de S distincte de p. La limite de f , lorsque x tend vers p à partir des valeurs de S , est L, si pour tout ε > 0 , il existe a δ > 0 tel que 0 < | x − p | < δ et x ∈ S implique que | f ( x ) − L | < ε . erreur harv : pas de cible : CITEREFBartleSherbert2000 ( aide )

Cette limite s'écrit souvent :

${\displaystyle L=\lim _{\stackrel {x\to p}{x\in S}}f(x).}$

La condition pour que f soit défini sur S est que S soit un sous-ensemble du domaine de f . Cette généralisation inclut comme cas particuliers des limites sur un intervalle, ainsi que des limites gauches de fonctions à valeurs réelles (par exemple, en prenant S comme un intervalle ouvert de la forme ), et des limites droites (par exemple, en prenant S être un intervalle ouvert de la forme ). Elle se prolonge aussi la notion de limite à sens unique vers les points d' extrémité inclus de (semi-) intervalles fermés, de sorte que la fonction racine carrée f ( x ) = √ x peut avoir des limites 0 lorsque x tend vers 0 au - dessus. ${\style d'affichage (-\infty ,a)}$${\style d'affichage (a,\infty )}$

Limites supprimées et non supprimées

La définition de limite donnée ici ne dépend pas de comment (ou si) f est défini à p . Bartle (1967) appelle cela une limite supprimée , car elle exclut la valeur de f à p . La limite non supprimée correspondante dépend de la valeur de f en p , si p est dans le domaine de f :

• Un nombre L est la limite non supprimée de f lorsque x tend vers p si, pour tout ε > 0 , il existe un δ > 0 tel que | x  −  p  | <  δ et x ∈ Dm ( f ) implique | f ( x ) −  L  | <  ε .

La définition est la même, sauf que le quartier | x  −  p  | <  δ inclut désormais le point p , contrairement au voisinage supprimé 0 < | x  −  p  | <  δ . Cela rend la définition d'une limite non supprimée moins générale. L'un des avantages de travailler avec des limites non supprimées est qu'elles permettent d'énoncer le théorème sur les limites des compositions sans aucune contrainte sur les fonctions (autre que l'existence de leurs limites non supprimées) ( Hubbard (2015) ).

Bartle (1967) note que bien que par « limite » certains auteurs entendent cette limite non supprimée, les limites supprimées sont les plus populaires. Par exemple, Apostol (1974) , Courant (1924) , Hardy (1921) , Rudin (1964) , Whittaker & Watson (1902) prennent tous "limite" pour signifier la limite supprimée. erreur harvtxt : pas de cible : CITEREFWhitakerWatson1902 ( aide )

Exemples

Inexistence de limite(s) unilatérale(s)

La fonction

${\displaystyle f(x)={\begin{cases}\sin {\frac {5}{x-1}}&{\text{ pour }}x<1\\0&{\text{ pour }}x =1\\{\frac {0.1}{x-1}}&{\text{ for }}x>1\end{cases}}}$

n'a pas de limite à (la limite de gauche n'existe pas en raison de la nature oscillatoire de la fonction sinus, et la limite de droite n'existe pas en raison du comportement asymptotique de la fonction réciproque), mais a une limite à tous les autres x -coordonnée. ${\style d'affichage x_{0}=1}$

La fonction

${\displaystyle f(x)={\begin{cases}1&x{\text{ rationnel }}\\0&x{\text{ irrational }}\end{cases}}}$

(aka, la fonction de Dirichlet ) n'a de limite à aucune coordonnée x .

Non-égalité des limites unilatérales

La fonction

${\displaystyle f(x)={\begin{cases}1&{\text{ pour }}x<0\\2&{\text{ pour }}x\geq 0\end{cases}}}$

a une limite à chaque coordonnée x non nulle (la limite est égale à 1 pour x négatif et égale à 2 pour x positif ). La limite à x = 0 n'existe pas (la limite de gauche vaut 1, alors que la limite de droite vaut 2).

Limites en un seul point

Les fonctions

${\displaystyle f(x)={\begin{cases}x&x{\text{ rationnel }}\\0&x{\text{ irrational }}\end{cases}}}$

et

${\displaystyle f(x)={\begin{cases}|x|&x{\text{ rationnel }}\\0&x{\text{ irrational }}\end{cases}}}$

les deux ont une limite à x = 0 et elle est égale à 0.

Limites à un nombre incalculable de points

La fonction

${\displaystyle f(x)={\begin{cases}\sin x&x{\text{ irrationnel }}\\1&x{\text{ rationnel }}\end{cases}}}$

a une limite à n'importe quelle coordonnée x de la forme , où n est un entier quelconque. ${\displaystyle {\frac {\pi }{2}}+2n\pi }$

Fonctions sur les espaces métriques

Supposons que M et N soient des sous-ensembles des espaces métriques A et B , respectivement, et f  : M → N est défini entre M et N , avec x ∈ M, p un point limite de M et L ∈ N . On dit que la limite de f lorsque x tend vers p est L et écrire

${\displaystyle \lim _{x\to p}f(x)=L}$

si la propriété suivante est vérifiée :

• Pour tout ε > 0, il existe a δ > 0 tel que d _B ( f ( x ), L ) < ε chaque fois que 0 <  d _A ( x ,  p ) <  δ .

Encore une fois, notez que p n'a pas besoin d'être dans le domaine de f , ni L n'a besoin d'être dans la plage de f , et même si f ( p ) est défini, il n'a pas besoin d'être égal à L .

Une autre définition utilisant le concept de voisinage est la suivante :

${\displaystyle \lim _{x\to p}f(x)=L}$

si, pour tout voisinage V de L dans B , il existe un voisinage U de p dans A tel que f (U M − { p }) V .

Fonctions sur les espaces topologiques

Supposons que X , Y sont des espaces topologiques avec Y un espace de Hausdorff . Soit p un point limite de Ω ⊆  X , et L ∈ Y . Pour une fonction f  : Ω → Y , on dit que la limite de f lorsque x tend vers p est L (ie, f ( x ) → L lorsque x → p ) et s'écrit

${\displaystyle \lim _{x\to p}f(x)=L}$

si la propriété suivante est vérifiée :

• Pour tout voisinage ouvert V de L , il existe un voisinage ouvert U de p tel que f ( U  ∩ Ω − { p }) V .

Cette dernière partie de la définition peut aussi être formulée « il existe un voisinage ouvert poinçonné U de p tel que f ( U ∩Ω) ⊆ V ».

Notez que le domaine de f n'a pas besoin de contenir p . Si c'est le cas, alors la valeur de f à p n'est pas pertinente pour la définition de la limite. En particulier, si le domaine de f est X  − { p } (ou tout de X ), alors la limite de f comme x → p existe et est égale à L si, pour tous les sous-ensembles de X de point limite p , le La limite de la restriction de f à existe et est égale à L . Parfois, ce critère est utilisé pour établir la non-existence de la limite bilatérale d'une fonction sur R en montrant que les limites unilatérales n'existent pas ou ne concordent pas. Une telle vision est fondamentale dans le domaine de la topologie générale , où les limites et la continuité en un point sont définies en termes de familles spéciales de sous-ensembles, appelés filtres , ou de séquences généralisées appelées réseaux .

Alternativement, l'exigence que Y soit un espace de Hausdorff peut être assouplie à l'hypothèse que Y soit un espace topologique général, mais alors la limite d'une fonction peut ne pas être unique. En particulier, on ne peut plus parler de limite d'une fonction en un point, mais plutôt d' une limite ou de l'ensemble des limites en un point.

Une fonction est continue en un point limite p de et dans son domaine si et seulement si f ( p ) est la (ou, dans le cas général, a ) limite de f ( x ) lorsque x tend vers p .

Limites impliquant l'infini

Limites à l'infini

Laissez , et . ${\displaystyle S\subseteq \mathbb {R} }$${\style d'affichage x\dans S}$${\displaystyle f:S\mapsto \mathbb {R} }$

La limite de f lorsque x tend vers l'infini est L , notée

${\displaystyle \lim _{x\to \infty }f(x)=L,}$

signifie que pour tout , il existe c tel que chaque fois que x  >  c . Ou, symboliquement : ${\displaystyle \varepsilon >0}$${\displaystyle |f(x)-L|<\varepsilon }$

${\displaystyle \forall \varepsilon >0\;\exists c\;\forall x>c:\;|f(x)-L|<\varepsilon }$.

De même, la limite de f lorsque x tend vers l'infini négatif est L , notée

${\displaystyle \lim _{x\to -\infty }f(x)=L,}$

signifie que pour tout il existe c tel que chaque fois que x  <  c . Ou, symboliquement : ${\displaystyle \varepsilon >0}$${\displaystyle |f(x)-L|<\varepsilon }$

${\displaystyle \forall \varepsilon >0\;\exists c\;\forall x<c:\;|f(x)-L|<\varepsilon }$.

Par exemple,

${\displaystyle \lim _{x\to -\infty }e^{x}=0.\,}$

Limites infinies

Pour une fonction dont les valeurs croissent sans limite, la fonction diverge et la limite habituelle n'existe pas. Cependant, dans ce cas, on peut introduire des limites avec des valeurs infinies. Laissez , et . L'énoncé la limite de f lorsque x se rapproche de a est l'infini , noté ${\displaystyle S\subseteq \mathbb {R} }$${\style d'affichage x\dans S}$${\displaystyle f:S\mapsto \mathbb {R} }$

${\displaystyle \lim _{x\to a}f(x)=\infty ,}$

signifie que pour tout il existe tel que chaque fois que${\style d'affichage N>0}$${\displaystyle \delta >0}$${\style d'affichage f(x)>N}$${\displaystyle 0<|xa|<\delta .}$

Ces idées peuvent être combinées de manière naturelle pour produire des définitions pour différentes combinaisons, telles que

${\displaystyle \lim _{x\to \infty }f(x)=\infty ,\lim _{x\to a^{+}}f(x)=-\infty .}$

Par exemple,

${\displaystyle \lim _{x\to 0^{+}}\ln x=-\infty .}$

Les limites impliquant l'infini sont liées au concept d' asymptotes .

Ces notions de limite tentent de fournir une interprétation de l'espace métrique aux limites à l'infini. En fait, ils sont cohérents avec la définition de l'espace topologique de la limite si

• un voisinage de −∞ est défini pour contenir un intervalle [−∞,  c ) pour un certain c  ∈  R ,
• est défini un voisinage de ∞ pour contenir un intervalle ( c , ∞] où c  ∈  R , et
• un voisinage de a ∈ R est défini de la manière habituelle espace métrique R .

Dans ce cas, R est un espace topologique et une fonction de la forme f :  X  →  Y avec X ,  Y ⊆  R est soumise à la définition d'une limite topologique. Notez qu'avec cette définition topologique, il est facile de définir des limites infinies aux points finis, qui n'ont pas été définies ci-dessus au sens métrique.

Notation alternative

De nombreux auteurs autorisent l'utilisation de la ligne réelle étendue par projection comme moyen d'inclure des valeurs infinies ainsi que la ligne réelle étendue . Avec cette notation, la droite réelle étendue est donnée par R {−∞, +∞} et la droite réelle étendue projectivement est R  ∪ {∞} où un voisinage de ∞ est un ensemble de la forme { x : | x | > c }. L'avantage est qu'on n'a besoin que de trois définitions de limites (gauche, droite et centrale) pour couvrir tous les cas. Comme présenté ci-dessus, pour un compte rendu complètement rigoureux, nous aurions besoin de considérer 15 cas distincts pour chaque combinaison d'infinis (cinq directions : −∞, gauche, centrale, droite et +∞ ; trois bornes : −∞, fini ou + ). Il y a aussi des écueils notables. Par exemple, lorsque vous travaillez avec la ligne réelle étendue, ne possède pas de limite centrale (ce qui est normal): ${\style d'affichage x^{-1}}$

${\displaystyle \lim _{x\to 0^{+}}{1 \over x}=+\infty ,\lim _{x\to 0^{-}}{1 \over x}=-\infty .}$

En revanche, lorsque l'on travaille avec la ligne réelle projective, infinités ( un peu comme 0) ne sont pas signés, donc, la limite centrale ne exist dans ce contexte:

${\displaystyle \lim _{x\to 0^{+}}{1 \over x}=\lim _{x\to 0^{-}}{1 \over x}=\lim _{x\to 0}{1 \over x}=\infty .}$

En fait, il existe une pléthore de systèmes formels contradictoires. Dans certaines applications de différentiation et d'intégration numériques , il est par exemple commode d'avoir des zéros signés . Une raison simple a à voir avec l'inverse de , à savoir qu'il est pratique pour être considéré comme vrai. De tels zéros peuvent être vus comme une approximation des infinitésimaux . ${\displaystyle \lim _{x\to 0^{-}}{x^{-1}}=-\infty }$${\displaystyle \lim _{x\to -\infty }{x^{-1}}=-0}$

Limites à l'infini pour les fonctions rationnelles

Il existe trois règles de base pour évaluer les limites à l'infini pour une fonction rationnelle f ( x ) = p ( x )/ q ( x ) : (où p et q sont des polynômes) :

• Si le degré de p est supérieur au degré de q , alors la limite est l'infini positif ou négatif selon les signes des coefficients dominants ;
• Si les degrés de p et q sont égaux, la limite est le coefficient dominant de p divisé par le coefficient dominant de q ;
• Si le degré de p est inférieur au degré de q , la limite est 0.

Si la limite à l'infini existe, elle représente une asymptote horizontale à y = L . Les polynômes n'ont pas d'asymptotes horizontales ; de telles asymptotes peuvent cependant se produire avec des fonctions rationnelles.

Fonctions de plusieurs variables

En notant que | x  −  p | représente une distance, la définition d'une limite peut être étendue aux fonctions de plusieurs variables. Dans le cas d'une fonction f  : R ² → R ,

${\displaystyle \lim _{(x,y)\to (p,q)}f(x,y)=L}$

si

pour tout ε > 0 il existe un δ > 0 tel que pour tout ( x , y ) avec 0 < ||( x , y ) − ( p , q )|| < δ, alors | f ( x , y ) −  L | < ε

où ||( x , y ) − ( p , q )|| représente la distance euclidienne . Cela peut être étendu à un nombre quelconque de variables.

Limites séquentielles

Soit f  : X → Y une application à partir d' un espace topologique X dans un espace séparé Y , p ∈ X un point limite de X et L ∈ Y .

La limite séquentielle de f lorsque x tend vers p est L si, pour toute suite ( x _n ) dans X − { p } qui converge vers p , la suite f ( x _n ) converge vers L .

Si L est la limite (au sens ci-dessus) de f lorsque x tend vers p , alors c'est aussi une limite séquentielle, cependant l'inverse n'a pas besoin d'être vérifié en général. Si de plus X est métrisable , alors L est la limite séquentielle de f lorsque x tend vers p si et seulement si c'est la limite (au sens ci-dessus) de f lorsque x tend vers p .

Autres caractérisations

En termes de séquences

Pour les fonctions sur la ligne réelle, une façon de définir la limite d'une fonction est en termes de limite de séquences. (Cette définition est généralement attribuée à Eduard Heine .) Dans ce cadre :

${\displaystyle \lim _{x\to a}f(x)=L}$

si, et seulement si, pour toutes les suites (avec différent de a pour tout n ) convergeant vers la suite converge vers . Il a été montré par Sierpiński en 1916 que prouver l'équivalence de cette définition et de la définition ci-dessus, nécessite et équivaut à une forme faible de l' axiome du choix . Notez que définir ce que cela signifie pour une séquence de converger vers nécessite la méthode epsilon, delta . ${\style d'affichage x_{n}}$${\style d'affichage x_{n}}$${\style d'affichage a}$${\style d'affichage f(x_{n})}$${\style d'affichage L}$${\style d'affichage x_{n}}$${\style d'affichage a}$

De même que ce fut le cas de la définition de Weierstrass, une définition plus générale de Heine s'applique aux fonctions définies sur des sous - ensembles de la ligne réelle. Soit f une fonction à valeur réelle de domaine Dm ( f ). Soit a la limite d'une suite d'éléments de Dm ( f ) \ { a }. Alors la limite (dans ce sens) de f est L lorsque x tend vers p si pour chaque suite  ∈  Dm ( f ) \ { a } (de sorte que pour tout n , n'est pas égal à a ) qui converge vers a , la suite converge à . C'est la même chose que la définition d'une limite séquentielle dans la section précédente obtenue en considérant le sous-ensemble Dm ( f ) de R comme un espace métrique avec la métrique induite. ${\style d'affichage x_{n}}$${\style d'affichage x_{n}}$${\style d'affichage f(x_{n})}$${\style d'affichage L}$

En calcul non standard

En calcul non standard, la limite d'une fonction est définie par :

${\displaystyle \lim _{x\to a}f(x)=L}$

si et seulement si pour tout , est infinitésimal quand est infinitésimal. Voici les nombres hyperréels et est l'extension naturelle de f aux nombres réels non standard. Keisler a prouvé qu'une telle définition hyperréelle de limite réduit la complexité du quantificateur de deux quantificateurs. D'autre part, Hrbacek écrit que pour que les définitions soient valables pour tous les nombres hyperréels, elles doivent être implicitement fondées sur la méthode ε-δ, et affirme que, du point de vue pédagogique, l'espoir que le calcul non standard puisse être fait sans les méthodes ε-δ ne peut pas être réalisé dans son intégralité. Bŀaszczyk et al. détailler l'utilité de la microcontinuité dans l'élaboration d'une définition transparente de la continuité uniforme, et caractériser la critique de Hrbacek comme une « complainte douteuse ». ${\displaystyle x\in \mathbb {R} ^{*}}$${\style d'affichage f^{*}(x)-L}$${\style d'affichage xa}$${\displaystyle \mathbb {R} ^{*}}$${\displaystyle f^{*}}$

En terme de proximité

Au congrès international de mathématiques de 1908, F. Riesz a introduit une autre manière de définir les limites et la continuité du concept appelée « proximité ». Un point est défini comme étant proche d'un ensemble si pour tout il y a un point tel que . Dans ce cadre, le ${\style d'affichage x}$${\displaystyle A\subseteq \mathbb {R} }$${\style d'affichage r>0}$${\style d'affichage a\dans A}$${\style d'affichage |xa|<r}$

${\displaystyle \lim _{x\to a}f(x)=L}$

si et seulement si pour tout , est proche chaque fois que est proche . Voici l'ensemble . Cette définition peut également être étendue aux espaces métriques et topologiques. ${\displaystyle A\subseteq \mathbb {R} }$${\style d'affichage L}$${\style d'affichage f(A)}$${\style d'affichage a}$${\style d'affichage A}$${\style d'affichage f(A)}$${\displaystyle \{f(x)|x\in A\}}$

Relation à la continuité

La notion de limite d'une fonction est très étroitement liée à la notion de continuité. Une fonction ƒ est dite continue en c si elle est à la fois définie en c et si sa valeur en c est égale à la limite de f lorsque x tend vers c :

${\displaystyle \lim _{x\to c}f(x)=f(c).}$

(Nous avons supposé ici que c est un point limite du domaine de f .)

Propriétés

Si une fonction f est à valeur réelle, alors la limite de f en p est L si et seulement si la limite droite et la limite gauche de f en p existent et sont égales à L .

La fonction f est continue en p si et seulement si la limite de f ( x ) lorsque x tend vers p existe et est égale à f ( p ). Si f  : M → N est une fonction entre les espaces métriques M et N , alors il est équivalent que f transforme toute suite dans M qui converge vers p en une suite dans N qui converge vers f ( p ).

Si N est un espace vectoriel normé , alors l'opération limite est linéaire dans le sens suivant : si la limite de f ( x ) lorsque x tend vers p est L et la limite de g ( x ) lorsque x tend vers p est P , alors le la limite de f ( x ) + g( x ) lorsque x s'approche de p est L + P . Si a est un scalaire du corps de base , alors la limite de af ( x ) lorsque x s'approche de p est aL .

Si f et g sont des fonctions à valeur réelle (ou à valeur complexe), alors prendre la limite d'une opération sur f ( x ) et g ( x ) (par exemple, , , , , ) sous certaines conditions est compatible avec l'opération de limites de f(x) et g(x) . Ce fait est souvent appelé le théorème algébrique limite . La condition principale nécessaire pour appliquer les règles suivantes est que les limites sur les membres de droite des équations existent (en d'autres termes, ces limites sont des valeurs finies incluant 0). De plus, l'identité pour la division nécessite que le dénominateur du côté droit soit non nul (la division par 0 n'est pas définie), et l'identité pour l'exponentiation nécessite que la base soit positive, ou zéro alors que l'exposant est positif (fini ). ${\style d'affichage f+g}$ ${\style d'affichage fg}$ ${\displaystyle f\fois g}$ ${\style d'affichage f/g}$ ${\style d'affichage f^{g}}$

${\displaystyle {\begin{matrice}\lim \limits _{x\to p}&(f(x)+g(x))&=&\lim \limits _{x\to p}f(x) +\lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)-g(x))&=&\lim \limits _{ x\to p}f(x)-\lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)\cdot g(x) )&=&\lim \limits _{x\to p}f(x)\cdot \lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}& (f(x)/g(x))&=&{\lim \limits _{x\to p}f(x)/\lim \limits _{x\to p}g(x)}\\\ lim \limits _{x\to p}&f(x)^{g(x)}&=&{\lim \limits _{x\to p}f(x)^{\lim \limits _{x\ à p}g(x)}}\end{matrice}}}$

Ces règles sont également valables pour les limites unilatérales, y compris lorsque p est ∞ ou −∞. Dans chaque règle ci-dessus, lorsque l'une des limites à droite est ∞ ou -∞, la limite à gauche peut parfois encore être déterminée par les règles suivantes.

• q + ∞ = ∞ si q ≠ −∞
• q × ∞ = ∞ si q > 0
• q × ∞ = −∞ si q < 0
• q / ∞ = 0 si q ≠ ∞ et q ≠ −∞
• ∞ ^q = 0 si q <0
• ∞ ^q = ∞ si q > 0
• q ^∞ = 0 si 0 < q < 1
• q ^∞ = ∞ si q > 1
• q ^−∞ = ∞ si 0 < q < 1
• q ^−∞ = 0 si q > 1

(voir aussi Ligne des nombres réels étendus ).

Dans d'autres cas, la limite à gauche peut encore exister, bien que la partie droite, appelée forme indéterminée , ne permette pas de déterminer le résultat. Cela dépend des fonctions f et g . Ces formes indéterminées sont :

• 0 / 0
• ±∞ / ±∞
• 0 × ±∞
• + −∞
• 0 ⁰
• ∞ ⁰
• 1 ^±∞

Voir plus loin la règle de L'Hôpital ci-dessous et le formulaire Indéterminé .

Limites des compositions de fonctions

En général, en sachant que

${\displaystyle \lim _{y\to b}f(y)=c}$et ,${\displaystyle \lim _{x\to a}g(x)=b}$

ça ne s'ensuit pas . Cependant, cette "règle de la chaîne" est valable si l'une des conditions supplémentaires suivantes est vérifiée : ${\displaystyle \lim _{x\to a}f(g(x))=c}$

• f ( b ) = c (c'est-à-dire que f est continue en b ), ou
• g ne prend pas la valeur b près de a (c'est-à-dire qu'il existe un tel que si alors ).${\displaystyle \delta >0}$${\displaystyle 0<|xa|<\delta }$${\style d'affichage |g(x)-b|>0}$

À titre d'exemple de ce phénomène, considérons les fonctions suivantes qui enfreignent les deux restrictions supplémentaires :

${\displaystyle f(x)=g(x)={\begin{cases}0&{\text{if }}x\neq 0\\1&{\text{if }}x=0\end{cases}} .}$

Puisque la valeur à f (0) est une discontinuité amovible ,

${\displaystyle \lim _{x\to a}f(x)=0}$pour tous .${\style d'affichage a}$

Ainsi, la règle de la chaîne naïve suggérerait que la limite de f ( f ( x )) est 0. Cependant, il est vrai que

${\displaystyle f(f(x))={\begin{cases}1&{\text{if }}x\neq 0\\0&{\text{if }}x=0\end{cases}}}$

et donc

${\displaystyle \lim _{x\to a}f(f(x))=1}$pour tous .${\style d'affichage a}$

Limites d'intérêt particulier

Fonctions rationnelles

Pour un entier non négatif et des constantes et , ${\style d'affichage n}$${\displaystyle a_{1},a_{2},a_{3},\ldots ,a_{n}}$${\displaystyle b_{1},b_{2},b_{3},\ldots ,b_{n}}$

• ${\displaystyle \lim _{x\to \infty }{\frac {a_{1}{x}^{n}+a_{2}{x}^{n-1}+a_{3}{x} ^{n-2}+...+a_{n}}{b_{1}{x}^{n}+b_{2}{x}^{n-1}+b_{3}{x} ^{n-2}+...+b_{n}}}={\frac {a_{1}}{b_{1}}}}$

Cela peut être prouvé en divisant à la fois le numérateur et le dénominateur par . Si le numérateur est un polynôme de degré supérieur, la limite n'existe pas. Si le dénominateur est de degré supérieur, la limite est 0. ${\style d'affichage x^{n}}$

Fonctions trigonométriques

• ${\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}=1}$
• ${\displaystyle \lim _{x\to 0}{\frac {1-\cos x}{x}}=0}$

Fonctions exponentielles

• ${\displaystyle \lim _{x\to 0}(1+x)^{\frac {1}{x}}=\lim _{r\to \infty }\left(1+{\frac {1} {r}}\right)^{r}=e}$
• ${\displaystyle \lim _{x\to 0}{\frac {e^{x}-1}{x}}=1}$
• ${\displaystyle \lim _{x\to 0}{\frac {e^{ax}-1}{bx}}={\frac {a}{b}}}$
• ${\displaystyle \lim _{x\to 0}{\frac {c^{ax}-1}{bx}}={\frac {a}{b}}\ln c}$
• ${\displaystyle \lim _{x\to 0^{+}}x^{x}=1}$

Fonctions logarithmiques

• ${\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1}$
• ${\displaystyle \lim _{x\to 0}{\frac {\ln(1+ax)}{bx}}={\frac {a}{b}}}$
• ${\displaystyle \lim _{x\to 0}{\frac {\log _{c}(1+ax)}{bx}}={\frac {a}{b\ln c}}}$

La règle de l'Hôpital

Cette règle utilise des dérivées pour trouver des limites de formes indéterminées 0/0 ou ±∞/∞ , et ne s'applique qu'à de tels cas. D'autres formes indéterminées peuvent être manipulées dans cette forme. Soient deux fonctions f ( x ) et g ( x ) , définies sur un intervalle ouvert I contenant le point limite désiré c , alors si :

1. ${\displaystyle \lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0,}$ ou , et${\displaystyle \lim _{x\to c}f(x)=\pm \lim _{x\to c}g(x)=\pm \infty }$
2. ${\style d'affichage f}$et sont dérivables sur , et${\style d'affichage g}$${\displaystyle I\setminus \{c\}}$
3. ${\style d'affichage g'(x)\neq 0}$pour tous , et${\displaystyle x\in I\setminus \{c\}}$
4. ${\displaystyle \lim _{x\to c}{\frac {f'(x)}{g'(x)}}}$ existe,

alors:

${\displaystyle \lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g '(X)}}}$

Normalement, la première condition est la plus importante.

Par exemple: ${\displaystyle \lim _{x\to 0}{\frac {\sin(2x)}{\sin(3x)}}=\lim _{x\to 0}{\frac {2\cos(2x) }{3\cos(3x)}}={\frac {2\cdot 1}{3\cdot 1}}={\frac {2}{3}}.}$

Sommes et intégrales

La spécification d'une limite infinie sur une sommation ou une intégrale est un raccourci courant pour spécifier une limite.

Une façon courte d'écrire la limite est . Un exemple important de limites de sommes telles que celles-ci sont les séries . ${\displaystyle \lim _{n\to \infty }\sum _{i=s}^{n}f(i)}$${\displaystyle \sum _{i=s}^{\infty }f(i)}$

Une façon courte d'écrire la limite est . ${\displaystyle \lim _{x\to \infty }\int _{a}^{x}f(t)\;dt}$${\displaystyle \int _{a}^{\infty }f(t)\;dt}$

Une façon courte d'écrire la limite est . ${\displaystyle \lim _{x\to -\infty }\int _{x}^{b}f(t)\;dt}$${\displaystyle \int _{-\infty }^{b}f(t)\;dt}$

Voir également

•  Notation Big O - Notation décrivant le comportement limitant
• Règle de L'Hôpital  – Règle mathématique pour évaluer certaines limites
• Liste des limites  – article de la liste Wikipédia
• Limite d'une séquence  - Valeur vers laquelle les termes d'une séquence "tendent"
• Limite supérieure et limite inférieure
• Net (mathématiques)  - Une généralisation d'une séquence de points
• Calcul non standard
• Théorème de la compression  - Sur le calcul des limites en délimitant une fonction entre deux autres fonctions
• Limite subséquente  - La limite d'une sous-séquence

Remarques

Les références

• Apostol, Tom M. (1974), Analyse mathématique (2 éd.), Addison-Wesley, ISBN 0-201-00288-4
• Bartle, Robert (1967), Les éléments de l'analyse réelle , Wiley
• Courant, Richard (1924), Vorlesungen über Differential- und Integralrechnung , Springer Verlag
• Hardy, GH (1921), Un cours de mathématiques pures , Cambridge University Press
• Hubbard, John H. (2015), Calcul vectoriel, algèbre linéaire et formes différentielles : une approche unifiée (cinquième éd.), Matrix Editions
• Page, Warren ; Hersh, Ruben ; Selden, Annie; et al., éd. (2002), " Media Highlights ", The College Mathematics , 33 (2) : 147-154, JSTOR  2687124.
• Rudin, Walter (1964), Principes d'analyse mathématique , McGraw-Hill
• Sutherland, WA (1975), Introduction aux espaces métriques et topologiques , Oxford: Oxford University Press, ISBN 0-19-853161-3
• Sherbert, Robert (2000), Introduction à l'analyse réelle , Wiley
• Whittaker ; Watson (1904), Un cours d'analyse moderne , Cambridge University Press

Liens externes

• Histoire MacTutor de Weierstrass.
• MacTutor Histoire de Bolzano
• Visual Calculus par Lawrence S. Husch , Université du Tennessee (2001)