Intégrale de ligne - Line integral

En mathématiques , une intégrale de ligne est une intégrale où la fonction à intégrer est évaluée le long d'une courbe . Les termes de l' intégrale de chemin , solidaires de la courbe , et intégrales curvilignes sont également utilisés; L'intégrale de contour est également utilisée, bien qu'elle soit généralement réservée aux intégrales de ligne dans le plan complexe .

La fonction à intégrer peut être un champ scalaire ou un champ vectoriel . La valeur de l'intégrale linéaire est la somme des valeurs du champ en tous les points de la courbe, pondérée par une fonction scalaire sur la courbe (généralement la longueur de l'arc ou, pour un champ vectoriel, le produit scalaire du champ vectoriel avec un différentiel vecteur dans la courbe). Cette pondération distingue l'intégrale de ligne des intégrales plus simples définies sur des intervalles . De nombreuses formules simples en physique, telles que la définition du travail comme , ont des analogues continus naturels en termes d'intégrales de ligne, dans ce cas , qui calcule le travail effectué sur un objet se déplaçant dans un champ électrique ou gravitationnel F le long d'un chemin . ${\displaystyle W=\mathbf {F} \cdot \mathbf {s} }$${\displaystyle \textstyle W=\int _{L}\mathbf {F} (\mathbf {s} )\cdot d\mathbf {s} }$${\style d'affichage L}$

Calcul vectoriel

En termes qualitatifs, une ligne intégrale en calcul vectoriel peut être considérée comme une mesure de l'effet total d'un champ de tenseur donné le long d'une courbe donnée. Par exemple, la ligne intégrale sur un champ scalaire (tenseur de rang 0) peut être interprétée comme l'aire sous le champ découpée par une courbe particulière. Cela peut être visualisé comme la surface créée par z = f ( x , y ) et une courbe C dans le plan xy . L'intégrale de la ligne de f serait la zone du "rideau" créé - lorsque les points de la surface qui sont directement au-dessus de C sont découpés.

Intégrale linéaire d'un champ scalaire

La ligne intégrale sur un champ scalaire f peut être considérée comme l'aire sous la courbe C le long d'une surface z = f ( x , y ), décrite par le champ.

Définition

Pour un champ scalaire où , la ligne intégrale le long d'une courbe lisse par morceaux est définie comme ${\displaystyle f\colon U\to \mathbb {R} }$${\displaystyle U\subseteq \mathbb {R} ^{n}}$ ${\displaystyle {\mathcal {C}}\sous-ensemble U}$

${\displaystyle \int _{\mathcal {C}}f(\mathbf {r} )\,ds=\int _{a}^{b}f\left(\mathbf {r} (t)\right) \gauche|\mathbf {r} '(t)\droit|\,dt.}$

où est une paramétrisation bijective arbitraire de la courbe telle que r ( a ) et r ( b ) donnent les extrémités de et a < b . Ici, et dans le reste de l'article, les barres de valeur absolue désignent la norme (euclidienne) standard d'un vecteur. ${\displaystyle \mathbf {r} \colon [a,b]\to {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

La fonction f est appelée l'intégrande, la courbe est le domaine d'intégration, et le symbole ds peut être intuitivement interprété comme une longueur d'arc élémentaire . Les intégrales linéaires des champs scalaires sur une courbe ne dépendent pas de la paramétrisation choisie r de . ${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

Géométriquement, lorsque le champ scalaire f est définie sur un plan ( n = 2) , son graphe est une surface z = f ( x , y ) dans l' espace, et l'intégrale de ligne donne le (signé) de section transversale zone délimitée par la courbe et le graphique de f . Voir l'animation à droite. ${\displaystyle {\mathcal {C}}}$

Dérivation

Pour une ligne intégrale sur un champ scalaire, l'intégrale peut être construite à partir d'une somme de Riemann en utilisant les définitions ci-dessus de f , C et une paramétrisation r de C . Cela peut être fait en partitionnant l' intervalle [ a , b ] en n sous-intervalles [ t _{i −1} , t _i ] de longueur Δ t = ( b − a )/ n , alors r ( t _i ) désigne un point, appelez-le un point d'échantillonnage, sur la courbe C . Nous pouvons utiliser l' ensemble des points d'échantillonnage { r ( t _i ): 1 ≤ i ≤ n } pour approximer la courbe C par un chemin polygonal en introduisant un morceau de droite entre chacun des points d'échantillonnage r ( t _{i −1} ) et r ( t _i ) . Nous marquons alors la distance entre chacun des points d'échantillonnage sur la courbe comme Δ de _{la i} . Le produit de f ( r ( t _i )) et Δ s _i peut être associé à la zone signée d'un rectangle dont la hauteur et la largeur de f ( r ( t _i )) et Δ de _{la i} , respectivement. Prendre la limite de la somme des termes lorsque la longueur des partitions tend vers zéro nous donne

${\displaystyle I=\lim _{\Delta s_{i}\to 0}\sum _{i=1}^{n}f(\mathbf {r} (t_{i}))\,\Delta s_ {je}.}$

Par le théorème de la valeur moyenne , la distance entre les points suivants sur la courbe, est

${\displaystyle \Delta s_{i}=\left|\mathbf {r} (t_{i}+\Delta t)-\mathbf {r} (t_{i})\right|\approx \left|\mathbf {r} '(t_{i})\right|\Delta t.}$

En substituant cela dans la somme de Riemann ci-dessus, on obtient

${\displaystyle I=\lim _{\Delta t\to 0}\sum _{i=1}^{n}f(\mathbf {r} (t_{i}))\left|\mathbf {r} '(t_{i})\right|\Delta t}$

qui est la somme de Riemann pour l'intégrale

${\displaystyle I=\int _{a}^{b}f(\mathbf {r} (t))\left|\mathbf {r} '(t)\right|dt.}$

Intégrale linéaire d'un champ de vecteurs

Définition

Pour un champ de vecteurs F : U ⊆ R ⁿ → R ⁿ , l'intégrale de ligne le long d' une lisse par morceaux courbe C ⊂ U , dans le sens de r , est définie comme

${\displaystyle \int _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt}$

où · est le produit scalaire , et r : [ a , b ] → C est une paramétrisation bijective de la courbe C telle que r ( a ) et r ( b ) donnent les extrémités de C .

Une ligne intégrale d'un champ scalaire est donc une ligne intégrale d'un champ de vecteurs, où les vecteurs sont toujours tangents à la ligne.

Les intégrales linéaires des champs de vecteurs sont indépendantes de la paramétrisation r en valeur absolue , mais elles dépendent de son orientation . En effet, une inversion de l'orientation de la paramétrisation change le signe de l'intégrale droite.

Du point de vue de la géométrie différentielle , l'intégrale de ligne d'un champ de vecteurs le long d' une courbe est l'intégrale de la 1-forme correspondante dans le isomorphisme musical (qui prend le champ de vecteurs pour le correspondant covecteur champ), au-dessus de la courbe considérée comme une immergé 1-collecteur.

Dérivation

La trajectoire d'une particule (en rouge) le long d'une courbe à l'intérieur d'un champ vectoriel. En partant de a , la particule trace le chemin C le long du champ vectoriel F . Le produit scalaire (ligne verte) de son vecteur tangent (flèche rouge) et du vecteur champ (flèche bleue) définit une aire sous une courbe, qui est équivalente à l'intégrale de la ligne du chemin. (Cliquez sur l'image pour une description détaillée.)

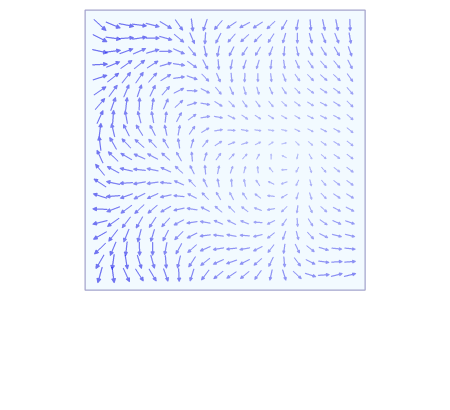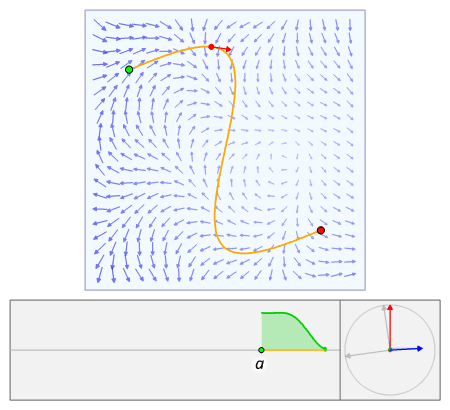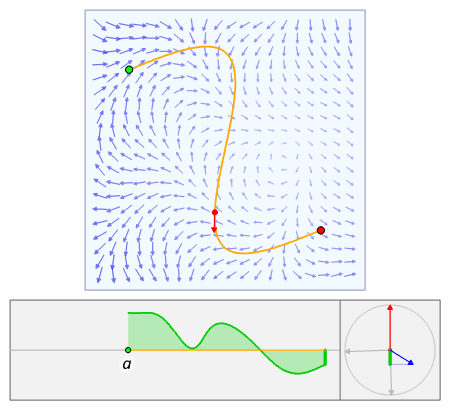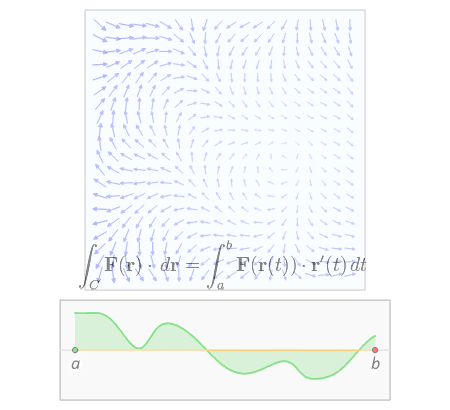
L'intégrale de ligne d'un champ vectoriel peut être dérivée d'une manière très similaire au cas d'un champ scalaire, mais cette fois avec l'inclusion d'un produit scalaire. En utilisant à nouveau les définitions ci-dessus de F , C et sa paramétrisation r ( t ) , nous construisons l'intégrale à partir d'une somme de Riemann . On partitionne l' intervalle [ a , b ] (qui est la plage des valeurs du paramètre t ) en n intervalles de longueur Δ t = ( b − a )/ n . Laisser t _i être le i e point [ a , b ] , puis r ( t _i ) nous donne la position du i ème point de la courbe. Cependant, au lieu de calculer les distances entre les points suivants, nous avons besoin de calculer leurs déplacements vecteurs, Δ r _i . Comme précédemment, évaluer F à tous les points de la courbe et prendre le produit scalaire avec chaque vecteur de déplacement nous donne la contribution infinitésimale de chaque partition de F sur C . Laisser la taille des partitions passer à zéro nous donne une somme

${\displaystyle I=\lim _{\Delta t\to 0}\sum _{i=1}^{n}\mathbf {F} (\mathbf {r} (t_{i}))\cdot \Delta \mathbf {r} _{i}}$

Par le théorème de la valeur moyenne , nous voyons que le vecteur de déplacement entre les points adjacents sur la courbe est

${\displaystyle \Delta \mathbf {r} _{i}=\mathbf {r} (t_{i}+\Delta t)-\mathbf {r} (t_{i})\approx \mathbf {r} ' (t_{i})\,\Delta t.}$

En substituant cela dans la somme de Riemann ci-dessus, on obtient

${\displaystyle I=\lim _{\Delta t\to 0}\sum _{i=1}^{n}\mathbf {F} (\mathbf {r} (t_{i}))\cdot \mathbf {r} '(t_{i})\,\Delta t,}$

qui est la somme de Riemann pour l'intégrale définie ci-dessus.

Indépendance du chemin

Si un champ vectoriel F est le gradient d'un champ scalaire G (c'est-à-dire si F est conservateur ), c'est-à-dire

${\displaystyle \mathbf {F} =\nabla G,}$

alors par la règle de la chaîne multivariable la dérivée de la composition de G et r ( t ) est

${\displaystyle {\frac {dG(\mathbf {r} (t))}{dt}}=\nabla G(\mathbf {r} (t))\cdot \mathbf {r} '(t)=\ mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)}$

qui se trouve être l'intégrande de l'intégrale de ligne de F sur r ( t ). Il s'ensuit, étant donné un chemin C , que

${\displaystyle \int _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt=\int _{a}^{b}{\frac {dG(\mathbf {r} (t))}{dt }}\,dt=G(\mathbf {r} (b))-G(\mathbf {r} (a)).}$

Autrement dit, l'intégrale de F sur C dépend uniquement des valeurs de G aux points r ( b ) et r ( a ), et est donc indépendante du chemin qui les sépare. Pour cette raison, une ligne intégrale d'un champ de vecteurs conservateur est appelée indépendante du chemin .

Applications

L'intégrale de ligne a de nombreuses utilisations en physique. Par exemple, le travail effectué sur une particule se déplaçant sur une courbe C à l' intérieur d'un champ de force représenté comme un champ vectoriel F est l'intégrale droite de F sur C .

Flux à travers une courbe

Pour un champ de vecteurs , F ( x , y ) = ( P ( x , y ), Q ( x , y )) , l' intégrale de droite passant par une courbe C ⊂ U , également appelée intégrale de flux , est définie en termes de paramétrisation lisse par morceaux r : [ a , b ] → C , r ( t ) = ( x ( t ), y ( t )) , comme : ${\displaystyle \mathbf {F} \colon U\subseteq \mathbb {R} ^{2}\to \mathbb {R} ^{2}}$

${\displaystyle \int _{C}\mathbf {F} (\mathbf {r} )\cdot d\mathbf {r} ^{\perp }=\int _{a}^{b}{\begin{bmatrix }P{\grand (}x(t),y(t){\grand )}\\Q{\grand (}x(t),y(t){\grand )}\end{bmatrice}}\ cdot {\begin{bmatrix}y'(t)\\-x'(t)\end{bmatrix}}~dt=\int _{a}^{b}-Q~dx+P~dy.}$

Ici • est le produit scalaire, et est la perpendiculaire dans le sens horaire du vecteur vitesse . ${\displaystyle \mathbf {r} '(t)^{\perp }=(y'(t),-x'(t))}$${\displaystyle \mathbf {r} '(t)=(x'(t),y'(t))}$

Le flux est calculé dans un sens orienté : la courbe C a une direction vers l'avant spécifiée de r ( a ) à r ( b ) , et le flux est compté comme positif lorsque F ( r ( t )) est du côté des aiguilles d'une montre vecteur vitesse avant r' ( t ) .

Intégrale de ligne complexe

En analyse complexe , l'intégrale de ligne est définie en termes de multiplication et d' addition de nombres complexes. Supposons que U est un ouvert du plan complexe C , f  : U → C est une fonction, et est une courbe de longueur finie, paramétrée par γ : [ a , b ] → L , où γ ( t ) = x ( t ) + iy ( t ) . L'intégrale de ligne ${\displaystyle L\sous-ensemble U}$

${\displaystyle \int _{L}f(z)\,dz}$

peut être défini en subdivisant l' intervalle [ a , b ] en a = t ₀ < t ₁ < ... < t _n = b et en considérant l'expression

${\displaystyle \sum _{k=1}^{n}f(\gamma (t_{k}))\,[\gamma (t_{k})-\gamma (t_{k-1})]= \sum _{k=1}^{n}f(\gamma _{k})\,\Delta \gamma _{k}.}$

L'intégrale est alors la limite de cette somme de Riemann lorsque les longueurs des intervalles de subdivision approchent de zéro.

Si la paramétrisation γ est continûment différentiable , l'intégrale de ligne peut être évaluée comme une intégrale d'une fonction d'une variable réelle:

${\displaystyle \int _{L}f(z)\,dz=\int _{a}^{b}f(\gamma (t))\gamma '(t)\,dt.}$

Lorsque L est une courbe fermée (les points initial et final coïncident), l'intégrale de ligne est souvent désignée, parfois appelée en ingénierie, intégrale cyclique . ${\textstyle \oint _{L}f(z)\,dz,}$

L'intégrale de droite par rapport à la différentielle complexe conjuguée est définie comme étant ${\displaystyle {\overline {dz}}}$

${\displaystyle \int _{L}f(z){\overline {dz}} :={\overline {\int _{L}{\overline {f(z)}}\,dz}}=\int _{a}^{b}f(\gamma (t)){\overline {\gamma '(t)}}\,dt.}$

Les intégrales linéaires des fonctions complexes peuvent être évaluées en utilisant un certain nombre de techniques. Le plus direct consiste à diviser en parties réelles et imaginaires, ce qui réduit le problème à l'évaluation de deux intégrales de ligne à valeur réelle. Le théorème de l'intégrale de Cauchy peut être utilisé pour assimiler l'intégrale de ligne d'une fonction analytique à la même intégrale sur une courbe plus pratique. Cela implique également que sur une courbe fermée englobant une région où f ( z ) est analytique sans singularités , la valeur de l'intégrale est simplement zéro, ou dans le cas où la région comprend des singularités, le théorème des résidus calcule l'intégrale en termes de singularités.

Exemple

Considérons la fonction f ( z ) = 1/ z , et soit le contour L le cercle unité dans le sens antihoraire autour de 0, paramétré par z( t ) = e ^it avec t dans [0, 2π] en utilisant l' exponentielle complexe . En remplaçant, on trouve :

${\displaystyle {\begin{aligned}\oint _{L}{\frac {1}{z}}\,dz&=\int _{0}^{2\pi }{\frac {1}{e^ {it}}}ie^{it}\,dt=i\int _{0}^{2\pi }e^{-it}e^{it}\,dt\\&=i\int _{ 0}^{2\pi }dt=i(2\pi -0)=2\pi i.\end{aligned}}}$

C'est un résultat typique de la formule intégrale de Cauchy et du théorème des résidus .

Relation entre l'intégrale de ligne complexe et l'intégrale de ligne du champ vectoriel

En considérant les nombres complexes comme des vecteurs à 2 dimensions , l'intégrale de ligne d'une fonction à valeurs complexes a des parties réelles et complexes égales à l'intégrale de ligne et à l'intégrale de flux du champ vectoriel correspondant à la fonction conjuguée Plus précisément, si paramétre L , et correspond à le champ de vecteurs alors : ${\style d'affichage f(z)}$${\displaystyle {\overline {f(z)}}.}$${\displaystyle \mathbf {r} (t)=(x(t),y(t))}$${\style d'affichage f(z)=u(z)+iv(z)}$${\displaystyle \mathbf {F} (x,y)={\overline {f(x+iy)}}=(u(x+iy),-v(x+iy)),}$

${\displaystyle {\begin{aligned}\int _{L}f(z)\,dz&=\int _{L}(u+iv)(dx+i\,dy)\\&=\int _{ L}(u,-v)\cdot (dx,dy)+i\int _{L}(u,-v)\cdot (dy,-dx)\\&=\int _{L}\mathbf { F} (\mathbf {r} )\cdot d\mathbf {r} +i\int _{L}\mathbf {F} (\mathbf {r} )\cdot d\mathbf {r} ^{\perp } .\end{aligné}}}$

Par le théorème de Cauchy , l'intégrale de gauche est nulle quand est analytique (satisfaisant aux équations de Cauchy-Riemann ) pour toute courbe fermée lisse L. De même, par le théorème de Green , les intégrales de droite sont nulles quand est irrotationnel ( sans boucle ) et incompressible (sans divergence ). En fait, les équations de Cauchy-Riemann pour sont identiques à l'annulation de curl et de divergence pour F . ${\style d'affichage f(z)}$${\displaystyle \mathbf {F} ={\overline {f(z)}}}$${\style d'affichage f(z)}$

Par le théorème de Green , l'aire d'une région délimitée par une courbe lisse, fermée et orientée positivement est donnée par l'intégrale Ce fait est utilisé, par exemple, dans la preuve du théorème de l' aire . ${\style d'affichage L}$${\displaystyle \textstyle {\frac {1}{2i}}\int _{L}{\overline {z}}\,dz.}$

Mécanique quantique

La formulation intégrale de chemin de la mécanique quantique se réfère en fait non pas à des intégrales de chemin dans ce sens mais à des intégrales fonctionnelles , c'est-à-dire des intégrales sur un espace de chemins, d'une fonction d' un chemin possible. Cependant, les intégrales de chemin au sens de cet article sont importantes en mécanique quantique ; par exemple, l'intégration de contours complexes est souvent utilisée pour évaluer les amplitudes de probabilité dans la théorie de la diffusion quantique .

Voir également

Les références

Liens externes

• "Integral over trajectoires" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Modules de l' Académie Khan :
  • "Introduction à la Ligne Intégrale"
  • "Exemple d'intégrale de ligne 1"
  • "Exemple d'intégrale de ligne 2 (partie 1)"
  • "Exemple d'intégrale de ligne 2 (partie 2)"
• Intégrale de chemin à PlanetMath .
• Intégrale linéaire d'un champ de vecteurs – Interactif