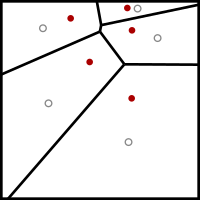
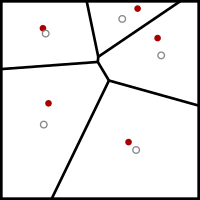
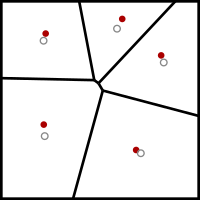
Algorithme de Lloyd - Lloyd's algorithm

Exemple de l'algorithme de Lloyd. Le diagramme de Voronoi des points courants à chaque itération est affiché. Les signes plus indiquent les centres de gravité des cellules Voronoi.

Itération 1

Itération 2

Itération 3

Itération 15

Dans la dernière image, les points sont très proches des centres de gravité des cellules de Voronoï. Une tessellation de Voronoï centroïde a été trouvée.

En génie électrique et en informatique , l'algorithme de Lloyd , également connu sous le nom d' itération ou de relaxation de Voronoi , est un algorithme nommé d'après Stuart P. Lloyd pour trouver des ensembles de points uniformément espacés dans des sous-ensembles d' espaces euclidiens et des partitions de ces sous-ensembles en bien formés et uniformément cellules convexes dimensionnées. Comme l' algorithme de clustering k -means étroitement lié , il trouve à plusieurs reprises le centre de gravité de chaque ensemble dans la partition, puis re-partitionne l'entrée selon lequel de ces centres est le plus proche. Dans ce paramètre, l'opération moyenne est une intégrale sur une région de l'espace et l'opération centroïde la plus proche donne des diagrammes de Voronoï .

Bien que l'algorithme puisse être appliqué le plus directement au plan euclidien , des algorithmes similaires peuvent également être appliqués à des espaces de dimension supérieure ou à des espaces avec d'autres métriques non euclidiennes . L'algorithme de Lloyd peut être utilisé pour construire des approximations proches des pavages de Voronoï centroïdes de l'entrée, qui peuvent être utilisées pour la quantification , le tramage et le pointillé . D'autres applications de l'algorithme de Lloyd incluent le lissage des maillages triangulaires dans la méthode des éléments finis .

Histoire

L'algorithme a été proposé pour la première fois par Stuart P. Lloyd de Bell Labs en 1957 comme technique de modulation par impulsions codées . Les travaux de Lloyd ont été largement diffusés, mais sont restés inédits jusqu'en 1982. Un algorithme similaire a été développé indépendamment par Joel Max et publié en 1960, c'est pourquoi l'algorithme est parfois appelé l'algorithme Lloyd-Max.

Description de l'algorithme

L'algorithme de Lloyd commence par un placement initial d'un certain nombre k de sites ponctuels dans le domaine d'entrée. Dans les applications de lissage de maillage, ce sont les sommets du maillage à lisser; dans d'autres applications, ils peuvent être placés au hasard ou en coupant un maillage triangulaire uniforme de taille appropriée avec le domaine d'entrée.

Il exécute ensuite à plusieurs reprises l'étape de relaxation suivante:

• Le diagramme de Voronoi des k sites est calculé.
• Chaque cellule du diagramme de Voronoi est intégrée et le centroïde est calculé.
• Chaque site est ensuite déplacé vers le centre de gravité de sa cellule Voronoi.

Intégration et calcul du centre de gravité

Comme les algorithmes de construction de diagramme de Voronoi peuvent être très non triviaux, en particulier pour les entrées de dimension supérieure à deux, les étapes de calcul de ce diagramme et de recherche des centres de gravité exacts de ses cellules peuvent être remplacées par une approximation.

Approximation

Une simplification courante consiste à utiliser une discrétisation appropriée de l'espace comme une fine grille de pixels, par exemple le tampon de texture dans le matériel graphique. Les cellules sont matérialisées sous forme de pixels, étiquetés avec leur ID de site correspondant. Le nouveau centre d'une cellule est approximé en calculant la moyenne des positions de tous les pixels affectés avec la même étiquette. Alternativement, les méthodes de Monte Carlo peuvent être utilisées, dans lesquelles des points d'échantillonnage aléatoires sont générés selon une distribution de probabilité sous-jacente fixe, assignés au site le plus proche et moyennés pour approximer le centroïde de chaque site.

Calcul exact

Bien que l'incorporation dans d'autres espaces soit également possible, cette élaboration suppose un espace euclidien en utilisant la norme L ² et discute les deux scénarios les plus pertinents, qui sont respectivement deux et trois dimensions.

Puisqu'une cellule de Voronoi est de forme convexe et renferme toujours son site, il existe des décompositions triviales en simplices faciles à intégrer:

• En deux dimensions, les bords de la cellule polygonale sont connectés à son site, créant un ensemble de triangles en forme de parapluie.
• En trois dimensions, la cellule est entourée de plusieurs polygones plans qui doivent d'abord être triangulés:
  • Calculez un centre pour la face du polygone, par exemple la moyenne de tous ses sommets.
  • La connexion des sommets d'une face polygonale avec son centre donne une triangulation plane en forme de parapluie.
  • Trivialement, un ensemble de tétraèdres est obtenu en reliant des triangles de la coque de la cellule avec le site de la cellule.

L'intégration d'une cellule et le calcul de son centroïde (centre de masse) sont maintenant donnés comme une combinaison pondérée des centroïdes de ses simplices (appelés ci-après ). ${\ textstyle \ mathbf {c} _ {i}}$

• Deux dimensions:
  • Pour un triangle, le centre de gravité peut être facilement calculé, par exemple en utilisant des coordonnées cartésiennes .
  • La pondération est calculée comme des rapports de surface simplex / cellule .
• Trois dimensions:
  • Le centre de gravité d'un tétraèdre se trouve à l'intersection de trois plans bissectrices et peut être exprimé sous la forme d'un produit matrice-vecteur.
  • La pondération est calculée en tant que rapports volumiques simplex / cellule .

Pour une cellule 2D avec n simples triangulaires et une aire accumulée (où est l' aire d'un triangle simplex), le nouveau centre de gravité de la cellule est calculé comme suit: ${\ textstyle A_ {C} = \ sum _ {i = 0} ^ {n} a_ {i}}$${\ textstyle a_ {i}}$

${\ displaystyle C = {\ frac {1} {A_ {C}}} \ sum _ {i = 0} ^ {n} \ mathbf {c} _ {i} a_ {i}}$

De manière analogue, pour une cellule 3D avec un volume de (où est le volume d'un tétraèdre simplex), le centroïde est calculé comme suit: ${\ textstyle V_ {C} = \ sum _ {i = 0} ^ {n} v_ {i}}$${\ textstyle v_ {i}}$

${\ displaystyle C = {\ frac {1} {V_ {C}}} \ sum _ {i = 0} ^ {n} \ mathbf {c} _ {i} v_ {i}}$

Convergence

Chaque fois qu'une étape de relaxation est effectuée, les points sont laissés dans une distribution légèrement plus uniforme: les points étroitement espacés s'éloignent les uns des autres et les points largement espacés se rapprochent. Dans une dimension, il a été démontré que cet algorithme converge vers un diagramme de Voronoï centroïde, également appelé pavage de Voronoï centroïde . Dans les dimensions supérieures, certains résultats de convergence légèrement plus faibles sont connus.

L'algorithme converge lentement ou, en raison de limitations de précision numérique, peut ne pas converger. Par conséquent, les applications réelles de l'algorithme de Lloyd s'arrêtent généralement une fois que la distribution est «assez bonne». Un critère de terminaison courant consiste à s'arrêter lorsque la distance maximale parcourue par un site quelconque dans une itération tombe en dessous d'un seuil prédéfini. La convergence peut être accélérée en relâchant excessivement les points, ce qui se fait en déplaçant chaque point ω fois la distance du centre de masse, en utilisant généralement une valeur légèrement inférieure à 2 pour ω .

Applications

La méthode de Lloyd était à l'origine utilisée pour la quantification scalaire, mais il est clair que la méthode s'étend également à la quantification vectorielle. En tant que tel, il est largement utilisé dans les techniques de compression de données en théorie de l'information . La méthode de Lloyd est utilisée en infographie parce que la distribution résultante a des caractéristiques de bruit bleu (voir aussi Couleurs du bruit ), ce qui signifie qu'il y a peu de composants basse fréquence qui pourraient être interprétés comme des artefacts. Il est particulièrement bien adapté à la sélection de positions d'échantillons pour le tramage . L'algorithme de Lloyd est également utilisé pour générer des dessins par points dans le style du pointillé . Dans cette application, les centres de gravité peuvent être pondérés sur la base d'une image de référence pour produire des illustrations pointillées correspondant à une image d'entrée.

Dans la méthode des éléments finis , un domaine d'entrée avec une géométrie complexe est partitionné en éléments avec des formes plus simples; par exemple, les domaines bidimensionnels (soit des sous-ensembles du plan euclidien, soit des surfaces en trois dimensions) sont souvent divisés en triangles. Il est important pour la convergence des méthodes des éléments finis que ces éléments soient bien formés; dans le cas des triangles, on préfère souvent les éléments qui sont presque des triangles équilatéraux. L'algorithme de Lloyd peut être utilisé pour lisser un maillage généré par un autre algorithme, en déplaçant ses sommets et en modifiant le modèle de connexion parmi ses éléments afin de produire des triangles plus étroitement équilatéraux. Ces applications utilisent généralement un plus petit nombre d'itérations de l'algorithme de Lloyd, l'arrêtant à la convergence, afin de préserver d'autres caractéristiques du maillage telles que les différences de taille d'élément dans différentes parties du maillage. Contrairement à une méthode de lissage différente, le lissage laplacien (dans lequel les sommets du maillage sont déplacés vers la moyenne des positions de leurs voisins), l'algorithme de Lloyd peut changer la topologie du maillage, conduisant à des éléments plus presque équilatéraux et évitant les problèmes avec enchevêtrement qui peut survenir avec le lissage laplacien. Cependant, le lissage laplacien peut être appliqué plus généralement aux maillages avec des éléments non triangulaires.

Différentes distances

L'algorithme de Lloyd est généralement utilisé dans un espace euclidien . La distance euclidienne joue deux rôles dans l'algorithme: elle sert à définir les cellules de Voronoi, mais elle correspond aussi au choix du centroïde comme point représentatif de chaque cellule, puisque le centroïde est le point qui minimise la distance euclidienne quadratique moyenne aux points de sa cellule. Des distances alternatives et des points centraux alternatifs au centre de gravité peuvent être utilisés à la place. Par exemple, Hausner (2001) a utilisé une variante de la métrique de Manhattan (avec des orientations localement variables) pour trouver un pavage d'une image par des carreaux approximativement carrés dont l'orientation s'aligne avec les caractéristiques d'une image, qu'il a utilisée pour simuler la construction de mosaïques en mosaïque . Dans cette application, malgré la variation de la métrique, Hausner a continué à utiliser les centroïdes comme points représentatifs de leurs cellules Voronoï. Cependant, pour les métriques qui diffèrent plus significativement d'Euclidienne, il peut être approprié de choisir le minimiseur de la distance quadratique moyenne comme point représentatif, à la place du centre de gravité.

Voir également

• L' algorithme Linde – Buzo – Gray , une généralisation de cet algorithme pour la quantification vectorielle
• Traversée la plus éloignée en premier , une méthode différente pour générer des points régulièrement espacés dans les espaces géométriques
• Le décalage moyen , une méthode connexe pour trouver les maxima d'une fonction de densité
• K-signifie ++

Les références

Liens externes

• DemoGNG.js Simulateur graphique Javascript pour l'algorithme LBG et d'autres modèles, comprend l'affichage des régions Voronoi