Recherche arborescente Monte Carlo - Monte Carlo tree search

Recherche d'arbre Monte-Carlo

Classer	Algorithme de recherche

En informatique , la recherche arborescente Monte Carlo ( MCTS ) est un algorithme de recherche heuristique pour certains types de processus de décision , notamment ceux utilisés dans les logiciels de jeux de société . Dans ce contexte, MCTS est utilisé pour résoudre l' arbre du jeu .

MCTS a été combiné avec des réseaux de neurones en 2016 pour l' ordinateur Go . Il a été utilisé dans d'autres jeux de société comme les échecs et le shogi , des jeux avec des informations incomplètes comme le bridge et le poker , ainsi que dans des jeux vidéo de stratégie au tour par tour (comme l' implémentation de Total War: Rome II dans la campagne de haut niveau IA). Le MCTS a également été utilisé dans les voitures autonomes, par exemple dans le logiciel Autopilot de Tesla.

Histoire

Méthode Monte-Carlo

La méthode de Monte Carlo , qui utilise un échantillonnage aléatoire pour des problèmes déterministes difficiles ou impossibles à résoudre par d'autres approches, remonte aux années 1940. Dans sa thèse de doctorat de 1987, Bruce Abramson a combiné la recherche minimax avec un modèle de résultat attendu basé sur des jeux aléatoires jusqu'à la fin, au lieu de la fonction d'évaluation statique habituelle . Abramson a déclaré que le modèle de résultat attendu "s'est avéré précis, exact, facilement estimable, calculable efficacement et indépendant du domaine". Il a expérimenté en profondeur avec Tic-tac-toe , puis avec des fonctions d'évaluation générées par machine pour Othello et Chess .

De telles méthodes ont ensuite été explorées et appliquées avec succès à la recherche heuristique dans le domaine de la démonstration automatique de théorèmes par W. Ertel, J. Schumann et C. Suttner en 1989, améliorant ainsi les temps de recherche exponentiels des algorithmes de recherche non informés tels que, par exemple, la recherche en largeur d'abord. , recherche en profondeur d'abord ou approfondissement itératif .

En 1992, B. Brügmann l'emploie pour la première fois dans un programme de Go-playing . En 2002, Chang et al. ont proposé l'idée de « déploiement et retour en arrière récursifs » avec des choix d'échantillonnage « adaptatifs » dans leur algorithme d'échantillonnage adaptatif à plusieurs étages (AMS) pour le modèle des processus de décision de Markov. AMS a été le premier travail à explorer l'idée de l' exploration et de l'exploitation basées sur UCB dans la construction d'arbres échantillonnés / simulés (Monte Carlo) et a été la principale graine pour UCT (Upper Confidence Trees).

Recherche arborescente Monte Carlo (SCTM)

Le classement des meilleurs programmes de Go-playing sur le serveur KGS depuis 2007. Depuis 2006, tous les meilleurs programmes utilisent la recherche arborescente Monte Carlo.

En 2006, inspiré par ces prédécesseurs, Rémi Coulom a décrit l'application de la méthode Monte Carlo à la recherche par arbre de jeu et a inventé le nom de recherche par arbre de Monte Carlo, L. Kocsis et Cs. Szepesvári a développé l'algorithme UCT (limites de confiance supérieures appliquées aux arbres), et S. Gelly et al. implémenté UCT dans leur programme MoGo. En 2008, MoGo a atteint le niveau dan (maître) en 9×9 Go, et le programme Fuego a commencé à gagner contre de solides joueurs amateurs en 9×9 Go.

En janvier 2012, le programme Zen a gagné 3:1 dans un match de Go sur un plateau 19×19 avec un joueur amateur de 2 dan . Google Deepmind a développé le programme AlphaGo , qui est devenu en octobre 2015 le premier programme Computer Go à battre un joueur de Go humain professionnel sans handicap sur une carte pleine grandeur 19x19. En mars 2016, AlphaGo a reçu un niveau honorifique de 9 dan (maître) en 19 × 19 Go pour avoir battu Lee Sedol dans un match de cinq matchs avec un score final de quatre matchs à un. AlphaGo représente une amélioration significative par rapport aux programmes Go précédents ainsi qu'une étape importante dans l'apprentissage automatique car il utilise la recherche arborescente Monte Carlo avec des réseaux de neurones artificiels (une méthode d' apprentissage en profondeur ) pour la politique (sélection de mouvement) et la valeur, ce qui lui confère une efficacité dépassant de loin les programmes précédents .

L'algorithme MCTS a également été utilisé dans des programmes qui jouent à d'autres jeux de société (par exemple Hex , Havannah , Game of the Amazons et Arimaa ), des jeux vidéo en temps réel (par exemple Ms. Pac-Man et Fable Legends ) et des jeux non déterministes (comme le skat , le poker , Magic: The Gathering ou Settlers of Catan ).

Principe d'opération

Le MCTS se concentre sur l'analyse des mouvements les plus prometteurs, en élargissant l' arbre de recherche sur la base d' un échantillonnage aléatoire de l'espace de recherche. L'application de la recherche arborescente Monte Carlo dans les jeux est basée sur de nombreux playouts, également appelés roll-outs . Dans chaque playout, le jeu est joué jusqu'à la fin en sélectionnant des coups au hasard. Le résultat final du jeu de chaque playout est ensuite utilisé pour pondérer les nœuds dans l'arbre du jeu afin que les meilleurs nœuds soient plus susceptibles d'être choisis dans les playouts futurs.

La façon la plus basique d'utiliser les playouts est d'appliquer le même nombre de playouts après chaque coup légal du joueur actuel, puis de choisir le coup qui a conduit au plus grand nombre de victoires. L'efficacité de cette méthode, appelée Pure Monte Carlo Game Search, augmente souvent avec le temps, car davantage de playouts sont attribués aux mouvements qui ont fréquemment abouti à la victoire du joueur actuel selon les playouts précédents. Chaque tour de recherche arborescente Monte Carlo se compose de quatre étapes :

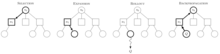
• Sélection : Partez de la racine R et sélectionnez les nœuds enfants successifs jusqu'à ce qu'un nœud feuille L soit atteint. La racine est l'état actuel du jeu et une feuille est tout nœud qui a un enfant potentiel à partir duquel aucune simulation (playout) n'a encore été initiée. La section ci-dessous en dit plus sur un moyen de biaiser le choix des nœuds enfants qui permet à l'arbre de jeu de s'étendre vers les mouvements les plus prometteurs, ce qui est l'essence de la recherche dans l'arbre Monte Carlo.
• Expansion : à moins que L ne termine le jeu de manière décisive (par exemple, victoire/défaite/nul) pour l'un ou l'autre des joueurs, créez un (ou plusieurs) nœuds enfants et choisissez le nœud C dans l'un d'entre eux. Les nœuds enfants sont tous les mouvements valides à partir de la position de jeu définie par L .
• Simulation : Terminez une lecture aléatoire à partir du nœud C . Cette étape est parfois aussi appelée playout ou rollout. Un playout peut être aussi simple que de choisir des coups aléatoires uniformes jusqu'à ce que la partie soit décidée (par exemple aux échecs, la partie est gagnée, perdue ou tirée au sort).
• Rétropropagation : utilisez le résultat de la diffusion pour mettre à jour les informations dans les nœuds sur le chemin de C à R .

Étape de recherche d'arbre de Monte Carlo.

Ce graphique montre les étapes impliquées dans une décision, chaque nœud indiquant le ratio de victoires par rapport au nombre total de parties à partir de ce point dans l'arbre de jeu pour le joueur que le nœud représente. Dans le diagramme de sélection, le noir est sur le point de se déplacer. Le nœud racine montre qu'il y a jusqu'à présent 11 victoires sur 21 playouts pour les blancs à partir de cette position. Il complète le total de 10/21 victoires noires affichées le long des trois nœuds noirs en dessous, chacun représentant un mouvement noir possible.

Si blanc perd la simulation, tous les nœuds le long de la sélection incrémentent leur nombre de simulations (le dénominateur), mais parmi eux seuls les nœuds noirs sont crédités de victoires (le numérateur). Si à la place les blancs gagnent, tous les nœuds le long de la sélection incrémenteront toujours leur nombre de simulations, mais parmi eux, seuls les nœuds blancs seront crédités de victoires. Dans les jeux où les tirages sont possibles, un tirage entraîne l'incrémentation du numérateur pour le noir et le blanc de 0,5 et le dénominateur de 1. Cela garantit que pendant la sélection, les choix de chaque joueur s'étendent vers les mouvements les plus prometteurs pour ce joueur, ce qui reflète le objectif de chaque joueur de maximiser la valeur de son coup.

Les rondes de recherche sont répétées tant que le temps alloué à un coup reste. Ensuite, le coup avec le plus de simulations effectuées (c'est-à-dire le plus grand dénominateur) est choisi comme réponse finale.

Recherche de jeu Pure Monte Carlo

Cette procédure de base peut être appliquée à n'importe quel jeu dont les positions ont nécessairement un nombre fini de coups et une longueur finie. Pour chaque position, tous les coups possibles sont déterminés : k jeux aléatoires sont joués jusqu'à la fin, et les scores sont enregistrés. Le coup menant au meilleur score est choisi. Les égalités sont rompues par des tirages au sort équitables. Pure Monte Carlo Game Search permet de jouer fort dans plusieurs jeux avec des éléments aléatoires, comme dans le jeu EinStein würfelt nicht! . Il converge vers un jeu optimal (car k tend vers l'infini) dans les jeux de remplissage de plateau avec un ordre de tour aléatoire, par exemple dans Hex avec un ordre de tour aléatoire. AlphaZero de DeepMind remplace l'étape de simulation par une évaluation basée sur un réseau de neurones.

Exploration et exploitation

La principale difficulté dans la sélection des nœuds enfants est de maintenir un certain équilibre entre l' exploitation de variantes profondes après des mouvements avec un taux de victoire moyen élevé et l' exploration de mouvements avec peu de simulations. La première formule pour équilibrer l'exploitation et l'exploration dans les jeux, appelée UCT ( Upper Confidence Bound 1 appliqué aux arbres ), a été introduite par Levente Kocsis et Csaba Szepesvári . UCT est basé sur la formule UCB1 dérivée par Auer, Cesa-Bianchi et Fischer et l'algorithme AMS (Adaptive Multi-stage Sampling) prouvablement convergent appliqué pour la première fois aux modèles de prise de décision à plusieurs étapes (en particulier, Markov Decision Processes ) par Chang, Fu, Hu et Marcus. Kocsis et Szepesvári recommandent de choisir dans chaque nœud de l'arbre de jeu le coup pour lequel l'expression a la valeur la plus élevée. Dans cette formule : ${\displaystyle {\frac {w_{i}}{n_{i}}}+c{\sqrt {\frac {\ln N_{i}}{n_{i}}}}}$

• w _i représente le nombre de victoires pour le nœud considéré après le i -ème coup
• n _i représente le nombre de simulations pour le nœud considéré après le i -ième mouvement
• N _i représente le nombre total de simulations après le i- ème mouvement exécuté par le nœud parent de celui considéré
• c est le paramètre théoriquement exploration égal à √ 2 ; en pratique généralement choisi empiriquement

La première composante de la formule ci-dessus correspond à l'exploitation ; il est élevé pour les coups avec un taux de victoire moyen élevé. La seconde composante correspond à l'exploration ; il est élevé pour les mouvements avec peu de simulations.

La plupart des implémentations contemporaines de la recherche arborescente Monte Carlo sont basées sur une variante de l'UCT qui remonte à l'algorithme d'optimisation de simulation AMS pour estimer la fonction de valeur dans les processus de décision de Markov à horizon fini (MDP) introduits par Chang et al. (2005) dans la recherche opérationnelle . (AMS a été le premier travail à explorer l'idée de l'exploration et de l'exploitation basées sur UCB dans la construction d'arbres échantillonnés/simulés (Monte Carlo) et a été le principal germe de l'UCT.)

Avantages et inconvénients

Bien qu'il ait été prouvé que l'évaluation des mouvements dans la recherche arborescente Monte Carlo converge vers minimax , la version de base de la recherche arborescente Monte Carlo ne converge que dans les jeux dits "Monte Carlo Perfect". Cependant, la recherche arborescente Monte Carlo offre des avantages significatifs par rapport à l' élagage alpha-bêta et aux algorithmes similaires qui minimisent l'espace de recherche.

En particulier, la recherche arborescente Monte Carlo pure n'a pas besoin d'une fonction d'évaluation explicite . La simple mise en œuvre de la mécanique du jeu suffit pour explorer l'espace de recherche (c'est-à-dire la génération des coups autorisés dans une position donnée et les conditions de fin de partie). En tant que tel, la recherche arborescente Monte Carlo peut être utilisée dans des jeux sans théorie développée ou dans le jeu en général .

L'arbre du jeu dans la recherche arborescente Monte Carlo se développe de manière asymétrique à mesure que la méthode se concentre sur les sous-arbres les plus prometteurs. Ainsi, il obtient de meilleurs résultats que les algorithmes classiques dans les jeux avec un facteur de branchement élevé .

Un inconvénient est que dans certaines positions, il peut y avoir des mouvements qui semblent superficiellement forts, mais qui conduisent en réalité à une perte via une ligne de jeu subtile. De tels "états pièges" nécessitent une analyse approfondie pour être traités correctement, en particulier lorsque vous jouez contre un joueur expert ; cependant, MCTS peut ne pas "voir" de telles lignes en raison de sa politique d'expansion sélective des nœuds. On pense que cela a pu être en partie la raison de la défaite d' AlphaGo lors de son quatrième match contre Lee Sedol . Essentiellement, la recherche tente d'élaguer les séquences qui sont moins pertinentes. Dans certains cas, un jeu peut conduire à une ligne de jeu très spécifique qui est significative, mais qui est négligée lors de l'élagage de l'arbre, et ce résultat est donc "hors du radar de recherche".

Améliorations

Diverses modifications de la méthode de recherche arborescente de base de Monte Carlo ont été proposées pour raccourcir le temps de recherche. Certains utilisent des connaissances spécialisées spécifiques à un domaine, d'autres non.

La recherche d'arbre Monte Carlo peut utiliser des lectures légères ou lourdes . Les playouts légers consistent en des mouvements aléatoires tandis que les playouts lourds appliquent diverses heuristiques pour influencer le choix des mouvements. Ces heuristiques peuvent utiliser les résultats des playouts précédents (par exemple l'heuristique de la dernière bonne réponse) ou la connaissance experte d'un jeu donné. Par exemple, dans de nombreux programmes de Go-playing, certains motifs de pierres dans une partie du plateau influencent la probabilité de se déplacer dans cette zone. Paradoxalement, jouer de manière sous-optimale dans les simulations rend parfois un programme de recherche arborescente Monte Carlo plus fort dans l'ensemble.

Motifs de hane (entourant les pierres adverses) utilisés dans les playouts par le programme MoGo. Il est avantageux pour le noir et le blanc de mettre une pierre sur le carré du milieu, à l'exception du motif le plus à droite où il privilégie uniquement le noir.

Des connaissances spécifiques au domaine peuvent être utilisées lors de la construction de l'arbre du jeu pour aider à l'exploitation de certaines variantes. Une telle méthode attribue des a priori non nuls au nombre de simulations gagnées et jouées lors de la création de chaque nœud enfant, ce qui conduit à des taux de victoire moyens artificiellement augmentés ou abaissés qui font que le nœud est choisi plus ou moins fréquemment, respectivement, dans l'étape de sélection. Une méthode connexe, appelée biais progressif , consiste à ajouter à la formule UCB1 un élément, où b _i est un score heuristique du i -ème coup. ${\displaystyle {\frac {b_{i}}{n_{i}}}}$

La recherche arborescente de base de Monte Carlo collecte suffisamment d'informations pour trouver les mouvements les plus prometteurs seulement après de nombreux tours ; jusque-là, ses mouvements sont essentiellement aléatoires. Cette phase exploratoire peut être considérablement réduite dans une certaine classe de jeux utilisant RAVE ( Rapid Action Value Estimation ). Dans ces jeux, les permutations d'une séquence de coups conduisent à la même position. Typiquement, ce sont des jeux de société dans lesquels un mouvement implique le placement d'une pièce ou d'une pierre sur le plateau. Dans de tels jeux, la valeur de chaque coup n'est souvent que légèrement influencée par les autres coups.

Dans RAVE, pour un nœud N d' arbre de jeu donné , ses nœuds enfants C _i stockent non seulement les statistiques de victoires dans les playouts démarrés dans le nœud N mais aussi les statistiques de victoires dans tous les playouts démarrés dans le nœud N et en dessous, s'ils contiennent move i (également lorsque le coup a été joué dans l'arbre, entre le nœud N et un playout). De cette façon, le contenu des nœuds de l'arbre est influencé non seulement par les coups joués immédiatement dans une position donnée, mais aussi par les mêmes coups joués plus tard.

RAVE sur l'exemple du morpion. Dans les nœuds rouges, les statistiques RAVE seront mises à jour après la simulation b1-a2-b3.

Lors de l'utilisation de RAVE, l'étape de sélection sélectionne le nœud pour lequel la formule UCB1 modifiée a la valeur la plus élevée. Dans cette formule, et représente le nombre de playouts gagnés contenant le coup i et le nombre de tous les playouts contenant le coup i , et la fonction doit être proche de un et de zéro pour des n _i et relativement grands , respectivement. L'une des nombreuses formules pour , proposées par D. Silver, dit que dans des positions équilibrées, on peut prendre , où b est une constante choisie empiriquement. ${\displaystyle (1-\beta (n_{i},{\tilde {n}}_{i})){\frac {w_{i}}{n_{i}}}+\beta (n_{i },{\tilde {n}}_{i}){\frac {{\tilde {w}}_{i}}{{\tilde {n}}_{i}}}+c{\sqrt { \frac {\ln t}{n_{i}}}}}$${\displaystyle {\tilde {w}}_{i}}$${\displaystyle {\tilde {n}}_{i}}$${\displaystyle \beta (n_{i},{\tilde {n}}_{i})}$${\displaystyle {\tilde {n}}_{i}}$${\displaystyle \beta (n_{i},{\tilde {n}}_{i})}$${\displaystyle \beta (n_{i},{\tilde {n}}_{i})={\frac {{\tilde {n}}_{i}}{n_{i}+{\tilde { n}}_{i}+4b^{2}n_{i}{\tilde {n}}_{i}}}}$

Les heuristiques utilisées dans la recherche arborescente Monte Carlo nécessitent souvent de nombreux paramètres. Il existe des méthodes automatisées pour régler les paramètres afin de maximiser le taux de victoire.

La recherche dans l'arborescence Monte Carlo peut être exécutée simultanément par de nombreux threads ou processus . Il existe plusieurs méthodes fondamentalement différentes de son exécution parallèle :

• Parallélisation des feuilles , c'est-à-dire exécution parallèle de plusieurs playouts à partir d'une feuille de l'arbre de jeu.
• Parallélisation racine , c'est-à-dire construire des arbres de jeu indépendants en parallèle et effectuer le mouvement en se basant sur les branches au niveau racine de tous ces arbres.
• Parallélisation d'arbres , c'est-à-dire construction parallèle d'un même arbre de jeu, protégeant les données des écritures simultanées soit avec un seul mutex global , soit avec plusieurs mutex, soit avec une synchronisation non bloquante .

Voir également

• AlphaGo , un programme Go utilisant la recherche arborescente Monte Carlo, l' apprentissage par renforcement et l'apprentissage en profondeur .
• AlphaGo Zero , un programme Go mis à jour utilisant la recherche par arbre Monte Carlo, l' apprentissage par renforcement et l'apprentissage en profondeur .
• AlphaZero , une version généralisée d'AlphaGo Zero utilisant la recherche arborescente Monte Carlo, l' apprentissage par renforcement et l'apprentissage en profondeur .
• Leela Chess Zero , une implémentation logicielle gratuite des méthodes d'échecs d'AlphaZero, qui fait actuellement partie des principaux programmes de jeu d'échecs.

Les références

Bibliographie

• Cameron Browne ; Edward Powley ; Daniel Whitehouse ; Simon Lucas ; Peter I. Cowling ; Philipp Rohlfshagen; Stephen Tavener ; Diego Perez ; Spyridon Samothrakis ; Simon Colton (mars 2012). "Une enquête sur les méthodes de recherche d'arbres de Monte Carlo". Transactions IEEE sur l'intelligence informatique et l'IA dans les jeux . 4 (1) : 1–43. CiteSeerX  10.1.1.297.3086 . doi : 10.1109/tciaig.2012.2186810 . S2CID  9316331 .

Liens externes

• Guide du débutant à Monte Carlo Tree Search