Éléments orbitaux - Orbital elements

Les éléments orbitaux sont les paramètres requis pour identifier de manière unique une orbite spécifique . En mécanique céleste, ces éléments sont considérés dans des systèmes à deux corps utilisant une orbite de Kepler . Il existe de nombreuses façons différentes de décrire mathématiquement la même orbite, mais certains schémas, chacun constitués d'un ensemble de six paramètres, sont couramment utilisés en astronomie et en mécanique orbitale .

Une orbite réelle et ses éléments changent au fil du temps en raison des perturbations gravitationnelles par d'autres objets et des effets de la relativité générale . Une orbite de Kepler est une approximation mathématique idéalisée de l'orbite à un moment donné.

Éléments képlériens

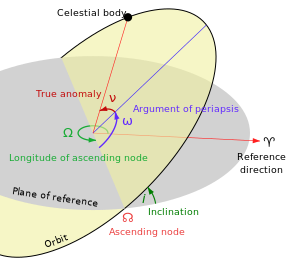
Dans ce diagramme, le plan orbital (jaune) coupe un plan de référence (gris). Pour les satellites en orbite terrestre, le plan de référence est généralement le plan équatorial de la Terre, et pour les satellites en orbite solaire, c'est le plan de l' écliptique . L'intersection s'appelle la ligne de nœuds , car elle relie le centre de masse aux nœuds ascendants et descendants. Le plan de référence, avec le point vernal ( ♈︎ ), établit un cadre de référence.

Les éléments orbitaux traditionnels sont les six éléments képlériens , d'après Johannes Kepler et ses lois du mouvement planétaire .

Vus depuis un référentiel inertiel , deux corps en orbite tracent des trajectoires distinctes. Chacune de ces trajectoires a son foyer au centre de masse commun . Vu d'un repère non inertiel centré sur l'un des corps, seule la trajectoire du corps opposé est apparente ; Les éléments képlériens décrivent ces trajectoires non inertielles. Une orbite a deux ensembles d'éléments képlériens en fonction du corps utilisé comme point de référence. Le corps de référence (généralement le plus massif) est appelé primaire , l'autre corps est appelé secondaire . Le primaire ne possède pas nécessairement plus de masse que le secondaire, et même lorsque les corps sont de masse égale, les éléments orbitaux dépendent du choix du primaire.

Deux éléments définissent la forme et la taille de l'ellipse :

Excentricité ( $e$ )—forme de l'ellipse, décrivant à quel point elle est allongée par rapport à un cercle (non marqué dans le diagramme).
Demi-grand axe ( $a$ ) — la somme des distances du périapse et de l'apoapse divisée par deux. Pour les orbites classiques à deux corps, le demi-grand axe est la distance entre les centres des corps, et non la distance des corps au centre de masse.

Deux éléments définissent l'orientation du plan orbital dans lequel l'ellipse est encastrée :

Inclinaison ( $i$ ) — inclinaison verticale de l'ellipse par rapport au plan de référence, mesurée au nœud ascendant (où l'orbite passe vers le haut par le plan de référence, l'angle vert $i$ dans le diagramme). L'angle d'inclinaison est mesuré perpendiculairement à la ligne d'intersection entre le plan orbital et le plan de référence. Trois points quelconques sur une ellipse définiront le plan orbital de l'ellipse. Le plan et l'ellipse sont tous deux des objets bidimensionnels définis dans un espace tridimensionnel.
Longitude du noeud ascendant ( $Ω$ ) - horizontalement oriente le noeud ascendant de l'ellipse (où l'orbite passe vers le haut à travers le plan de référence, symbolisée par $☊$ ) par rapport à l'image de référence point vernal (symbolisé par ♈︎). Elle est mesurée dans le plan de référence, et est représenté comme étant l'angle vert $Ω$ dans le diagramme.

Les deux éléments restants sont les suivants :

Argument de périgée ( $ω$ ) définit l'orientation de l'ellipse dans le plan orbital, selon un angle mesuré à partir du noeud ascendant au périgée (le point le plus proche de l'objet par satellite vient à l'objet principal autour duquel elle est en orbite, l'angle bleu $ω$ dans Le diagramme).
Anomalie vraie ( $ν$ , $θ$ , ou $f$ ) à l' époque ( $t 0$ ) définit la position du corps en orbite le long de l'ellipse à un moment précis (le "epoch").

L' anomalie moyenne $M$ est un "angle" fictif mathématiquement commode qui varie linéairement avec le temps, mais qui ne correspond pas à un angle géométrique réel. Il peut être converti en l' anomalie vraie $ν$ , qui ne représente l'angle réel géométrique dans le plan de l'ellipse, entre périgée (approche la plus proche du corps central) et la position de l'objet en orbite à un moment donné. Ainsi, l'anomalie vraie apparaît comme l'angle rouge $ν$ dans le diagramme et l'anomalie moyenne n'apparaît pas.

Les angles d'inclinaison, la longitude du nœud ascendant et l'argument du périapse peuvent également être décrits comme les angles d'Euler définissant l'orientation de l'orbite par rapport au système de coordonnées de référence.

Notez que des trajectoires non elliptiques existent également, mais ne sont pas fermées, et ne sont donc pas des orbites. Si l'excentricité est supérieure à un, la trajectoire est une hyperbole . Si l'excentricité est égale à un et le moment cinétique est nul, la trajectoire est radiale . Si l'excentricité est un et qu'il y a un moment cinétique, la trajectoire est une parabole .

Paramètres requis

Étant donné un référentiel inertiel et une époque arbitraire (un instant spécifié), exactement six paramètres sont nécessaires pour définir sans ambiguïté une orbite arbitraire et non perturbée.

C'est parce que le problème contient six degrés de liberté . Celles-ci correspondent aux trois dimensions spatiales qui définissent la position ( $x$ , $y$ , $z$ dans un système de coordonnées cartésiennes ), plus la vitesse dans chacune de ces dimensions. Ceux-ci peuvent être décrits comme des vecteurs d'états orbitaux , mais c'est souvent une façon peu pratique de représenter une orbite, c'est pourquoi les éléments képlériens sont couramment utilisés à la place.

Parfois, l'époque est considérée comme un "septième" paramètre orbital, plutôt que comme une partie du cadre de référence.

Si l'époque est définie comme étant au moment où l'un des éléments est nul, le nombre d'éléments quelconques est réduit à cinq. (Le sixième paramètre est toujours nécessaire pour définir l'orbite ; il est simplement mis à zéro numériquement par convention ou "déplacé" dans la définition de l'époque par rapport à l'heure de l'horloge du monde réel.)

Paramétrages alternatifs

Les éléments képlériens peuvent être obtenus à partir de vecteurs d'états orbitaux (un vecteur tridimensionnel pour la position et un autre pour la vitesse) par des transformations manuelles ou avec un logiciel informatique.

D'autres paramètres orbitaux peuvent être calculés à partir des éléments képlériens tels que la période , l' apoapsis et le périapsis . (En orbite autour de la Terre, les deux derniers termes sont appelés apogée et périgée.) Il est courant de spécifier la période au lieu du demi-grand axe dans les ensembles d'éléments képlériens, car chacun peut être calculé à partir de l'autre à condition que la gravité standard le paramètre , $GM$ , est donné pour le corps central.

Au lieu de l' anomalie moyenne à l' époque , l' anomalie moyenne $M$ , la longitude moyenne , l' anomalie vraie $ν 0$ , ou (rarement) l' anomalie excentrique pourrait être utilisée.

L'utilisation, par exemple, de « l'anomalie moyenne » au lieu de « l'anomalie moyenne à l'époque » signifie que le temps $t$ doit être spécifié comme un septième élément orbital. Parfois, on suppose que l'anomalie moyenne est nulle à l'époque (en choisissant la définition appropriée de l'époque), ne laissant que les cinq autres éléments orbitaux à spécifier.

Différents ensembles d'éléments sont utilisés pour divers corps astronomiques. L'excentricité, $e$ , et soit le demi-grand axe, $a$ , soit la distance de périapse, $q$ , sont utilisés pour spécifier la forme et la taille d'une orbite. La longitude du noeud ascendant, $Ω$ , l'inclinaison, $i$ , et l'argument de périgée, $ω$ , ou la longitude de périgée, $π$ , spécifier l'orientation de l'orbite dans son plan. Soit la longitude à l'époque, $L 0$ , l'anomalie moyenne à l'époque, $M 0$ , soit l'heure de passage au périhélie, $T 0$ , sont utilisées pour spécifier un point connu de l'orbite. Les choix effectués dépendent si l'équinoxe de printemps ou le nœud sont utilisés comme référence principale. Le demi-grand axe est connu si le mouvement moyen et la masse gravitationnelle sont connus.

Il est également assez courant de voir soit l'anomalie moyenne ( $M$ ) soit la longitude moyenne ( $L$ ) exprimées directement, sans $M 0$ ni $L 0$ comme étapes intermédiaires, comme une fonction polynomiale par rapport au temps. Cette méthode d'expression consolidera le mouvement moyen ( $n$ ) dans le polynôme comme l'un des coefficients. L'apparence sera que $L$ ou $M$ sont exprimés d'une manière plus compliquée, mais nous semblerons avoir besoin d'un élément orbital de moins.

Le mouvement moyen peut également être masqué derrière des citations de la période orbitale $P$ .

Ensembles d'éléments orbitaux
Objet	Éléments utilisés
Planète majeure	$e, un, i, Ω, π, L 0$
Comète	$e, q, i, Ω, ω, T 0$
Astéroïde	$e, un, i, Ω, ω, M 0$
Éléments à deux lignes	$e, i, Ω, ω, n, M 0$

Transformations de l'angle d'Euler

Les angles $Ω$ , $i$ , $ω$ sont les angles d' Euler (correspondant à $α$ , $β$ , $γ$ dans la notation utilisée dans cet article) caractérisant l'orientation du système de coordonnées

$x̂$ , $ŷ$ , $ẑ$ du repère inertiel $Î$ , $Ĵ$ , $K̂$

où:

$Î$ , $Ĵ$ est dans le plan équatorial du corps central. $Î$ est dans la direction de l'équinoxe de printemps. $Ĵ$ est perpendiculaire à $Î$ et avec $Î$ définit le plan de référence. $K̂$ est perpendiculaire au plan de référence. Les éléments orbitaux des corps (planètes, comètes, astéroïdes, ...) du système solaire utilisent généralement l' écliptique comme plan.
$x̂$ , $ŷ$ sont dans le plan orbital et avec $x̂$ dans la direction du péricentre ( périapsis ). $ẑ$ est perpendiculaire au plan de l'orbite. $ŷ$ est mutuellement perpendiculaire à $x̂$ et $ẑ$ .

Ensuite, la transformation de la $Î$ , $Ĵ$ , $K$ coordonnées de trame à la $x$ , $ŷ$ , $ẑ$ cadre avec les angles d' Euler $Ω$ , $i$ , $ω$ est la suivante :

{\begin{aligned}x_{1}&=\cos \Omega \cdot \cos \omega -\sin \Omega \cdot \cos i\cdot \sin \omega \ ;\\x_{2}& =\sin \Omega \cdot \cos \omega +\cos \Omega \cdot \cos i\cdot \sin \omega \ ;\\x_{3}&=\sin i\cdot \sin \omega ;\\\ ,\\y_{1}&=-\cos \Omega \cdot \sin \omega -\sin \Omega \cdot \cos i\cdot \cos \omega \ ;\\y_{2}&=-\sin \ Omega \cdot \sin \omega +\cos \Omega \cdot \cos i\cdot \cos \omega \ ;\\y_{3}&=\sin i\cdot \cos \omega \ ;\\\,\\ z_{1}&=\sin i\cdot \sin \Omega \ ;\\z_{2}&=-\sin i\cdot \cos \Omega \ ;\\z_{3}&=\cos i\ ; \\\,\end{aligné}}

\left[{\begin{array}{ccc}x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\\z_{1}&z_{2 }&z_{3}\end{array}}\right]=\left[{\begin{array}{ccc}\cos \omega &\sin \omega &0\\-\sin \omega &\cos \omega &0 \\0&0&1\end{array}}\right]\,\left[{\begin{array}{ccc}1&0&0\\0&\cos i&\sin i\\0&-\sin i&\cos i\end{array }}\right]\,\left[{\begin{array}{ccc}\cos \Omega &\sin \Omega &0\\-\sin \Omega &\cos \Omega &0\\0&0&1\end{array} }\droit]\,;

où

{\begin{aligned}\mathbf {\hat {x}} &=x_{1}\mathbf {\hat {I}} +x_{2}\mathbf {\hat {J}} +x_{ 3}\mathbf {\hat {K}} ~;\\\mathbf {\hat {y}} &=y_{1}\mathbf {\hat {I}} +y_{2}\mathbf {\hat { J}} +y_{3}\mathbf {\hat {K}} ~;\\\mathbf {\hat {z}} &=z_{1}\mathbf {\hat {I}} +z_{2} \mathbf {\hat {J}} +z_{3}\mathbf {\hat {K}} ~.\\\,\end{aligned}}

La transformation inverse, qui calcule les 3 coordonnées dans le système IJK étant donné les 3 (ou 2) coordonnées dans le système xyz, est représentée par la matrice inverse. Selon les règles de l' algèbre matricielle , la matrice inverse du produit des 3 matrices de rotation est obtenue en inversant l'ordre des trois matrices et en intervertissant les signes des trois angles d'Euler.

La transformation de $x$ , $ŷ$ , $ẑ$ angles d'Euler $Ω$ , $i$ , $ω$ est la suivante :

{\begin{aligned}\Omega &=\operatorname {arg} \left(-z_{2},z_{1}\right)\\i&=\operatorname {arg} \left(z_{3} ,{\sqrt {{z_{1}}^{2}+{z_{2}}^{2}}}\right)\\\omega &=\operatorname {arg} \left(y_{3}, x_{3}\right)\\\,\end{aligned}}

où $arg(x, y)$ signifie l'argument polaire qui peut être calculé avec la fonction standard atan2(y,x) disponible dans de nombreux langages de programmation.

Prédiction d'orbite

Dans des conditions idéales d'un corps central parfaitement sphérique et de perturbations nulles, tous les éléments orbitaux sauf l' anomalie moyenne sont des constantes. L'anomalie moyenne change linéairement avec le temps, mise à l'échelle par le mouvement moyen ,

n={\sqrt {\frac {\mu }{a^{3}}}}.

Par conséquent , si à un instant $t 0$ les paramètres orbitaux sont $[e 0, a 0, i 0, Ω 0, ω 0, M 0]$ , alors les éléments au moment $t = t 0 + AT$ est donné par $[e 0, un 0, i 0, Ω 0, w 0, M 0 + n ôt]$

Perturbations et variance élémentaire

Non perturbé, à deux corps , newtoniens orbites sont toujours des sections coniques , de sorte que les éléments de Kepler définissent une ellipse , parabole ou une hyperbole . Les orbites réelles ont des perturbations, donc un ensemble donné d'éléments képlériens décrit avec précision une orbite uniquement à l'époque. L'évolution des éléments orbitaux a lieu en raison de l' attraction gravitationnelle de corps autres que le primaire, de la non - sphéricité du primaire, de la traînée atmosphérique , des effets relativistes , de la pression de rayonnement , des forces électromagnétiques , etc.

Les éléments képlériens peuvent souvent être utilisés pour produire des prédictions utiles à des moments proches de l'époque. Alternativement, les trajectoires réelles peuvent être modélisées comme une séquence d'orbites képlériennes qui osculent ("embrasser" ou toucher) la trajectoire réelle. Elles peuvent aussi être décrites par les équations dites planétaires, équations différentielles qui se présentent sous différentes formes développées par Lagrange , Gauss , Delaunay , Poincaré , ou Hill .

Éléments à deux lignes

Les paramètres des éléments Keplerian peuvent être encodés sous forme de texte dans un certain nombre de formats. Le plus courant d'entre eux est le format NASA / NORAD « éléments à deux lignes » (TLE), conçu à l'origine pour être utilisé avec des cartes perforées à 80 colonnes, mais toujours utilisé car il s'agit du format le plus courant et peut être manipulé facilement par tous. stockages de données modernes ainsi.

Selon l'application et l'orbite de l'objet, les données dérivées des TLE de plus de 30 jours peuvent devenir peu fiables. Les positions orbitales peuvent être calculées à partir des TLE via les algorithmes SGP / SGP4 / SDP4 / SGP8 / SDP8.

Exemple d'élément de deux lignes :

1 27651U 03004A   07083.49636287  .00000119  00000-0  30706-4 0  2692
2 27651 039.9951 132.2059 0025931 073.4582 286.9047 14.81909376225249

Variables de Delaunay

Les éléments orbitaux de Delaunay ont été introduits par Charles-Eugène Delaunay lors de son étude du mouvement de la Lune . Communément appelées variables de Delaunay , il s'agit d'un ensemble de variables canoniques , qui sont des coordonnées d'angle d'action . Les angles sont des sommes simples de certains des angles képlériens :

$\ell =M+\omega +\Omega ~:$ la longitude moyenne
$g=\omega +\Omega ~:$ la longitude du périapse , et
$h=\Omega ~:$ la longitude du nœud ascendant

ainsi que leurs respectifs moments conjugués , $L$ , $G$ , et $H$ . Les moments $L$ , $G$ et $H$ sont les variables d' action et sont des combinaisons plus élaborées des éléments képlériens $a$ , $e$ et $i$ .

Les variables de Delaunay sont utilisées pour simplifier les calculs perturbatifs en mécanique céleste, par exemple lors de l'étude des oscillations de Kozai-Lidov dans les systèmes triples hiérarchiques. L'avantage des variables de Delaunay est qu'elles restent bien définies et non singulières (sauf pour $h$ , qui peut être toléré) lorsque $e$ et/ou $i$ sont très petits : Lorsque l'orbite de la particule à tester est très proche de la circulaire ( ), ou très presque « plat » ( ). $e\environ 0$ ${\style d'affichage i\environ 0}$

Voir également

Longitude apparente
Famille d' astéroïdes, astéroïdes qui partagent des éléments orbitaux appropriés similaires
Angle bêta
éphémérides
Modèle géopotentiel
Vecteurs d'état orbitaux
Éléments orbitaux appropriés
Orbite oscillante

Les références

Liens externes

Gurfil, Pini (2005). « Paramètres d'Euler en tant qu'éléments orbitaux non singuliers dans les orbites quasi-équatoriales ». J. Guid. Contrôle Dynamique . 28 (5) : 1079-1084. Bibcode : 2005JGCD ... 28.1079G . doi : 10.2514/1.14760 .

"Tutoriel" . AMSAT . Éléments képlériens. Archivé de l'original le 14 octobre 2002.

"Tutoriel Orbites" . marine.rutgers.edu .

"Visualiseur d'éléments orbitaux" . orbitalmechanics.info .

Rapport n° 3 (PDF) . celestrak (Rapport). Piste spatiale. Commandement de la défense aérospatiale de l'Amérique du Nord (NORAD). – un traitement sérieux des éléments orbitaux

"FAQ" . Célestrak . Éléments à deux lignes. Archivé de l'original le 26 mars 2016.

"Les éphémérides en ligne JPL HORIZONS" . – fournit également des éléments orbitaux pour un grand nombre d'objets du système solaire

"Paramètres orbitaux moyens" . ssd.jpl.nasa.gov . Satellites planétaires. JPL / NASA.

"Initiation à l'export" . ssd.jpl.nasa.gov . éphémérides planétaires et lunaires du JPL. JPL / NASA.

"Vecteurs d'état : VEC2TLE" . MindSpring (logiciel). Archivé de l'original le 3 mars 2016. – accès au logiciel VEC2TLE

"Fonction 'iauPlan94 ' " ( source du logiciel C ). Bibliothèque AIU SOFA C. – éléments orbitaux des grandes planètes

Languages

In other projects