Quaternions et rotation spatiale - Quaternions and spatial rotation

Les quaternions unitaires , appelés versors , fournissent une notation mathématique pratique pour représenter les orientations spatiales et les rotations des éléments dans l'espace tridimensionnel. Plus précisément, ils codent des informations sur une rotation axe-angle autour d'un axe arbitraire. Rotation et orientation escouades ont des applications dans l' infographie , vision par ordinateur , la robotique , la navigation , la dynamique moléculaire , la dynamique de vol , mécanique orbitale de satellites , et la texture cristallographique analyse.

Lorsqu'ils sont utilisés pour représenter la rotation, les quaternions unitaires sont également appelés quaternions de rotation car ils représentent le groupe de rotation 3D . Lorsqu'ils sont utilisés pour représenter une orientation (rotation par rapport à un système de coordonnées de référence), ils sont appelés quaternions d'orientation ou quaternions d'attitude . Une rotation spatiale autour d'un point fixe de radians autour d'un axe unitaire qui désigne l' axe d'Euler est donnée par le quaternion , où et . ${\displaystyle \theta }$${\style d'affichage (X,Y,Z)}$${\style d'affichage (C,X\,S,Y\,S,Z\,S)}$${\displaystyle C=\cos(\theta /2)}$${\displaystyle S=\sin(\theta /2)}$

Par rapport aux matrices de rotation , les quaternions sont plus compacts, efficaces et numériquement stables . Par rapport aux angles d'Euler , ils sont plus simples à composer et évitent le problème de blocage du cardan . Cependant, ils ne sont pas aussi intuitifs et faciles à comprendre que les angles d'Euler. Et, en raison de la nature périodique du sinus et du cosinus, les angles de rotation différant précisément de la période naturelle seront codés en quaternions identiques et les angles récupérés seront limités à (en radians ). ${\style d'affichage [0,2\pi ]}$

Utiliser des quaternions comme rotations

Dans l'espace à 3 dimensions, selon le théorème de rotation d' Euler , toute rotation ou séquence de rotations d'un corps rigide ou d'un système de coordonnées autour d'un point fixe équivaut à une seule rotation d'un angle donné autour d'un axe fixe (appelé axe d'Euler ) qui passe par le point fixe. L'axe d'Euler est généralement représenté par un vecteur unitaire u → ( dans l'image). Par conséquent, toute rotation en trois dimensions peut être représentée comme une combinaison d'un vecteur u → et d'un scalaire . ${\displaystyle \theta }$ ${\displaystyle {\hat {e}}}$  ${\displaystyle \theta }$

Les quaternions donnent un moyen simple de coder cette représentation axe-angle en quatre nombres et peuvent être utilisés pour appliquer la rotation correspondante à un vecteur de position , représentant un point par rapport à l' origine dans R ³ . Les vecteurs euclidiens tels que (2, 3, 4) ou ( a _x ,  a _y ,  a _z ) peuvent être réécrits comme 2  i + 3  j + 4  k ou a _x  i + a _y  j + a _z  k , où i , j , k sont des vecteurs unitaires représentant les trois axes cartésiens (traditionnellement x , y , z ), et obéissent également aux règles de multiplication des unités de quaternions fondamentales.

Par conséquent, une rotation d'angle autour de l'axe défini par le vecteur unitaire ${\displaystyle \theta }$

${\displaystyle {\vec {u}}=(u_{x},u_{y},u_{z})=u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{ z}\mathbf {k} }$

peut être représenté par un quaternion. Cela peut être fait en utilisant une extension de la formule d' Euler :

${\displaystyle \mathbf {q} =e^{{\frac {\theta }{2}}{(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\ mathbf {k} )}}=\cos {\frac {\theta }{2}}+(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf { k} )\sin {\frac {\theta }{2}}}$

On peut montrer que la rotation souhaitée peut être appliquée à un vecteur ordinaire dans l' espace à 3 dimensions, considéré comme un quaternion avec une coordonnée réelle égale à zéro, en évaluant la conjugaison de  p par  q : ${\displaystyle \mathbf {p} =(p_{x},p_{y},p_{z})=p_{x}\mathbf {i} +p_{y}\mathbf {j} +p_{z} \mathbf {k} }$

${\displaystyle \mathbf {p'} =\mathbf {q} \mathbf {p} \mathbf {q} ^{-1}}$

en utilisant le produit de Hamilton , où p = ( p _x ′,  p _y ′,  p _z ′) est le nouveau vecteur de position du point après la rotation. Dans une implémentation programmatique, la conjugaison est réalisée en construisant un quaternion dont la partie vectorielle est p et la partie réelle est égale à zéro, puis en effectuant la multiplication du quaternion. La partie de vecteur de la quaternion résultant est le vecteur souhaité p ' .

Mathématiquement, cette opération porte l' ensemble de tous les quaternions « purs » p (ceux dont la partie réelle est égale à zéro) - qui constituent un espace tridimensionnel parmi les quaternions - en lui-même, par la rotation souhaitée autour de l'axe u , par l'angle . (Chaque quaternion réel est transporté en lui-même par cette opération. Mais pour les rotations dans l'espace tridimensionnel, nous ignorons les quaternions réels.)

La rotation est dans le sens horaire si notre ligne de visée pointe dans la même direction que u → .

Dans ce cas, q est un quaternion unité et

${\displaystyle \mathbf {q} ^{-1}=e^{-{\frac {\theta }{2}}{(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )}}=\cos {\frac {\theta }{2}}-(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_ {z}\mathbf {k} )\sin {\frac {\theta }{2}}.}$

Il s'ensuit que la conjugaison par le produit de deux quaternions est la composition des conjugaisons par ces quaternions : Si p et q sont des quaternions unitaires, alors la rotation (conjugaison) par  pq est

${\displaystyle \mathbf {pq} {\vec {v}}(\mathbf {pq} )^{-1}=\mathbf {pq} {\vec {v}}\mathbf {q} ^{-1} \mathbf {p} ^{-1}=\mathbf {p} (\mathbf {q} {\vec {v}}\mathbf {q} ^{-1})\mathbf {p} ^{-1} }$,

ce qui revient à tourner (conjuguer) par  q puis par  p . La composante scalaire du résultat est nécessairement nulle.

Le quaternion inverse d'une rotation est la rotation opposée, puisque . Le carré d'une rotation de quaternion est une rotation de deux fois l'angle autour du même axe. Plus généralement q ⁿ est une rotation de  n fois l'angle autour du même axe que q . Cela peut être étendu à n réel arbitraire , permettant une interpolation douce entre les orientations spatiales; voir Slerp . ${\displaystyle \mathbf {q} ^{-1}(\mathbf {q} {\vec {v}}\mathbf {q} ^{-1})\mathbf {q} ={\vec {v}} }$

Deux quaternions de rotation peuvent être combinés en un quaternion équivalent par la relation :

${\displaystyle \mathbf {q} '=\mathbf {q} _{2}\mathbf {q} _{1}}$

dans laquelle q ′ correspond à la rotation q ₁ suivie de la rotation q ₂ . (Notez que la multiplication de quaternions n'est pas commutative .) Ainsi, un nombre arbitraire de rotations peut être composé ensemble puis appliqué comme une seule rotation.

Exemple d'opération de conjugaison

Conjuguer p par q renvoie à l'opération p ↦ qpq ^-1 .

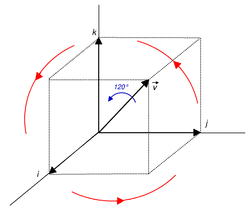
Considérons la rotation f autour de l'axe , avec un angle de rotation de 120°, ou${\displaystyle {\vec {v}}=\mathbf {i} +\mathbf {j} +\mathbf {k} }$2 π/3 radians .

${\displaystyle \alpha ={\frac {2\pi }{3}}}$

La longueur de v → est √ 3 , l'angle de la moitié est??/3(60°) avec cosinus 1/2, ( cos 60° = 0.5 ) et sinus √ 3/2, ( sin 60° 0,866 ). On a donc affaire à une conjugaison par le quaternion unité

${\displaystyle {\begin{aligned}u&=\cos {\frac {\alpha }{2}}+\sin {\frac {\alpha }{2}}\cdot {\frac {1}{\|{ \vec {v}}\|}}{\vec {v}}\\&=\cos {\frac {\pi }{3}}+\sin {\frac {\pi }{3}}\cdot {\frac {1}{\sqrt {3}}}{\vec {v}}\\&={\frac {1}{2}}+{\frac {\sqrt {3}}{2}} \cdot {\frac {1}{\sqrt {3}}}{\vec {v}}\\&={\frac {1}{2}}+{\frac {\sqrt {3}}{2 }}\cdot {\frac {\mathbf {i} +\mathbf {j} +\mathbf {k} }{\sqrt {3}}}\\&={\frac {1+\mathbf {i} + \mathbf {j} +\mathbf {k} }{2}}\end{aligned}}}$

Si f est la fonction de rotation,

${\displaystyle f(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )=u(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} ) u^{-1}}$

On peut prouver que l'inverse d'un quaternion unité est obtenu simplement en changeant le signe de ses composantes imaginaires. En conséquence,

${\displaystyle u^{-1}={\dfrac {1-\mathbf {i} -\mathbf {j} -\mathbf {k} }{2}}}$

et

${\displaystyle f(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )={\dfrac {1+\mathbf {i} +\mathbf {j} +\mathbf {k} }{2}}(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} ){\dfrac {1-\mathbf {i} -\mathbf {j} -\mathbf {k} }{2}}}$

Cela peut être simplifié, en utilisant les règles ordinaires de l'arithmétique des quaternions, pour

${\displaystyle f(a\mathbf {i} +b\mathbf {j} +c\mathbf {k} )=c\mathbf {i} +a\mathbf {j} +b\mathbf {k} }$

Comme prévu, la rotation correspond au maintien d'un cube fixe en un point et à sa rotation de 120° autour de la grande diagonale passant par le point fixe (observez comment les trois axes sont permutés cycliquement ).

Matrice de rotation dérivée du quaternion

Une rotation de quaternion (avec ) peut être algébriquement manipulée en une rotation matricielle , où est la matrice de rotation donnée par : ${\displaystyle \mathbf {p'} =\mathbf {q} \mathbf {p} \mathbf {q} ^{-1}}$${\displaystyle \mathbf {q} =q_{r}+q_{i}\mathbf {i} +q_{j}\mathbf {j} +q_{k}\mathbf {k} }$ ${\displaystyle \mathbf {p'} =\mathbf {Rp} }$${\displaystyle \mathbf {R} }$

${\displaystyle {\begin{aligned}\mathbf {R} &={\begin{bmatrix}1-2s(q_{j}^{2}+q_{k}^{2})&2s(q_{i} q_{j}-q_{k}q_{r})&2s(q_{i}q_{k}+q_{j}q_{r})\\2s(q_{i}q_{j}+q_{k }q_{r})&1-2s(q_{i}^{2}+q_{k}^{2})&2s(q_{j}q_{k}-q_{i}q_{r})\\ 2s(q_{i}q_{k}-q_{j}q_{r})&2s(q_{j}q_{k}+q_{i}q_{r})&1-2s(q_{i}^{ 2}+q_{j}^{2})\end{bmatrix}}\end{aligned}}}$

Ici et si q est un quaternion unité, . ${\displaystyle s=||q||^{-2}}$${\displaystyle s=1^{-2}=1}$

Ceci peut être obtenu en utilisant le calcul vectoriel et l'algèbre linéaire si nous exprimons et en tant que parties scalaires et vectorielles et utilisons la formule de l'opération de multiplication dans l'équation . Si nous écrivons comme , comme et comme , où , notre équation se transforme en . En utilisant la formule de multiplication de deux quaternions exprimés en parties scalaire et vectorielle, ${\displaystyle \mathbf {p} }$${\displaystyle \mathbf {q} }$${\displaystyle \mathbf {p'} =\mathbf {q} \mathbf {p} \mathbf {q} ^{-1}}$${\displaystyle \mathbf {p} }$${\displaystyle (0,\ \mathbf {p} )}$${\displaystyle \mathbf {p} '}$${\displaystyle (0,\ \mathbf {p} ')}$${\displaystyle \mathbf {q} }$${\displaystyle (q_{r},\ \mathbf {v} )}$${\displaystyle \mathbf {v} =(q_{i},q_{j},q_{k})}$${\displaystyle (0,\ \mathbf {p} ')=(q_{r},\ \mathbf {v} )(0,\ \mathbf {p} )s(q_{r},\ -\mathbf { v} )}$

${\displaystyle (r_{1},\ {\vec {v}}_{1})(r_{2},\ {\vec {v}}_{2})=(r_{1}r_{2 }-{\vec {v}}_{1}\cdot {\vec {v}}_{2},\ r_{1}{\vec {v}}_{2}+r_{2}{\ vec {v}}_{1}+{\vec {v}}_{1}\times {\vec {v}}_{2}),}$

cette équation peut être réécrite comme

${\displaystyle {\begin{aligned}(0,\ \mathbf {p} ')=&\ ((q_{r},\ \mathbf {v} )(0,\ \mathbf {p} ))s( q_{r},\ -\mathbf {v} )\\(0,\ \mathbf {p} ')=&\ (q_{r}0-\mathbf {v} \cdot \mathbf {p} ,\ q_{r}\mathbf {p} +0\mathbf {v} +\mathbf {v} \times \mathbf {p} )s(q_{r},\ -\mathbf {v} )\\(0, \ \mathbf {p} ')=&\ s(-\mathbf {v} \cdot \mathbf {p} ,\ q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )(q_{r},\ -\mathbf {v} )\\(0,\ \mathbf {p} ')=&\ s(-\mathbf {v} \cdot \mathbf {p} q_{r} -(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )\cdot (-\mathbf {v} ),\ (-\mathbf {v} \cdot \mathbf {p } )(-\mathbf {v} )+q_{r}(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )+(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )\times (-\mathbf {v} ))\\(0,\ \mathbf {p} ')=&\ s(-\mathbf {v} \ cdot \mathbf {p} q_{r}+q_{r}\mathbf {v} \cdot \mathbf {p} ,\ \mathbf {v} (\mathbf {v} \cdot \mathbf {p} )+q_ {r}^{2}\mathbf {p} +q_{r}\mathbf {v} \times \mathbf {p} +\mathbf {v} \times (q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p } ))\\(0,\ \mathbf {p} ')=&\ (0,\ s(\mathbf {v} \otimes \mathbf {v} +q_{r}^{2}\mathbf {I } +2q_{r}[\mathbf {v} ]_{\times }+[\mathbf {v} ]_{\times }^{2})\mathbf {p} ),\end{aligned}}}$

où désigne le produit extérieur , est la matrice d' identité et est la matrice de transformation qui , multipliée par la droite avec un vecteur , donne le produit vectoriel . ${\displaystyle \otimes }$${\displaystyle \mathbf {I} }$${\displaystyle [\mathbf {v} ]_{\times }}$${\displaystyle \mathbf {u} }$ ${\displaystyle \mathbf {v} \times \mathbf {u} }$

Puisque , nous pouvons identifier comme , qui, lors de l'expansion, devrait donner l'expression écrite sous forme matricielle ci-dessus. ${\displaystyle \mathbf {p} '=\mathbf {R} \mathbf {p} }$${\displaystyle \mathbf {R} }$${\displaystyle s(\mathbf {v} \otimes \mathbf {v} +q_{r}^{2}\mathbf {I} +2q_{r}[\mathbf {v} ]_{\times }+[ \mathbf {v} ]_{\times }^{2})}$

Récupération de la représentation axe-angle

L'expression fait tourner tout quaternion vectoriel autour d'un axe donné par le vecteur par l'angle , où et dépend du quaternion . ${\displaystyle \mathbf {q} \mathbf {p} \mathbf {q} ^{-1}}$ ${\displaystyle \mathbf {p} }$${\displaystyle \mathbf {a} }$${\displaystyle \theta }$${\displaystyle \mathbf {a} }$${\displaystyle \theta }$${\displaystyle \mathbf {q} =q_{r}+q_{i}\mathbf {i} +q_{j}\mathbf {j} +q_{k}\mathbf {k} }$

${\displaystyle \mathbf {a} }$et peut être trouvé à partir des équations suivantes: ${\displaystyle \theta }$

${\style d'affichage (a_{x},a_{y},a_{z})\ =\ {\frac {(q_{i},q_{j},q_{k})}{\sqrt {q_{i }^{2}+q_{j}^{2}+q_{k}^{2}}}}}$

${\displaystyle \theta \ =\ 2\operatorname {atan2} \left({\sqrt {q_{i}^{2}+q_{j}^{2}+q_{k}^{2}}}, q_{r}\droit),}$

où est l' arctangente à deux arguments . ${\displaystyle \mathrm {atan2} }$

Des précautions doivent être prises lorsque le quaternion s'approche d'un scalaire , car en raison de la dégénérescence, l'axe d'une rotation d'identité n'est pas bien défini.

La composition des rotations spatiales

Un avantage de la formulation en quaternions de la composition de deux rotations R _B et R _A est qu'elle donne directement l' axe et l'angle de rotation de la rotation composite R _C = R _B R _A .

Soit le quaternion associé à une rotation spatiale R construit à partir de son axe de rotation S avec l'angle de rotation autour de cet axe. Le quaternion associé est donné par ${\displaystyle \varphi }$

${\displaystyle S=\cos {\frac {\varphi }{2}}+\sin {\frac {\varphi }{2}}\mathbf {S} .}$

Alors la composition de la rotation R _B avec R _A est la rotation R _C = R _B R _A d'axe de rotation et d'angle défini par le produit des quaternions

${\displaystyle A=\cos {\frac {\alpha }{2}}+\sin {\frac {\alpha }{2}}\mathbf {A} \quad {\text{and}}\quad B= \cos {\frac {\beta }{2}}+\sin {\frac {\beta }{2}}\mathbf {B} ,}$

C'est

${\displaystyle C=\cos {\frac {\gamma }{2}}+\sin {\frac {\gamma }{2}}\mathbf {C} ={\Big (}\cos {\frac {\ beta }{2}}+\sin {\frac {\beta }{2}}\mathbf {B} {\Big )}{\Big (}\cos {\frac {\alpha }{2}}+\ sin {\frac {\alpha }{2}}\mathbf {A} {\Big )}.}$

Développez ce produit pour obtenir

${\displaystyle \cos {\frac {\gamma }{2}}+\sin {\frac {\gamma }{2}}\mathbf {C} ={\Big (}\cos {\frac {\beta } {2}}\cos {\frac {\alpha }{2}}-\sin {\frac {\beta }{2}}\sin {\frac {\alpha }{2}}\mathbf {B} \ cdot \mathbf {A} {\Gros )}+{\Gros (}\sin {\frac {\beta }{2}}\cos {\frac {\alpha }{2}}\mathbf {B} +\ sin {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\mathbf {A} +\sin {\frac {\beta }{2}}\sin {\frac { \alpha }{2}}\mathbf {B} \times \mathbf {A} {\Grand )}.}$

Divisez les deux côtés de cette équation par l'identité, qui est la loi des cosinus sur une sphère ,

${\displaystyle \cos {\frac {\gamma }{2}}=\cos {\frac {\beta }{2}}\cos {\frac {\alpha }{2}}-\sin {\frac { \beta }{2}}\sin {\frac {\alpha }{2}}\mathbf {B} \cdot \mathbf {A} ,}$

et calculer

${\displaystyle \tan {\frac {\gamma }{2}}\mathbf {C} ={\frac {\tan {\frac {\beta }{2}}\mathbf {B} +\tan {\frac {\alpha }{2}}\mathbf {A} +\tan {\frac {\beta }{2}}\tan {\frac {\alpha }{2}}\mathbf {B} \times \mathbf { A} }{1-\tan {\frac {\beta }{2}}\tan {\frac {\alpha }{2}}\mathbf {B} \cdot \mathbf {A} }}.}$

C'est la formule de Rodrigues pour l'axe d'une rotation composite défini en fonction des axes des deux rotations. Il a dérivé cette formule en 1840 (voir page 408).

Les trois axes de rotation A , B , et C forment un triangle sphérique et les angles dièdres entre les plans formés par les côtés de ce triangle sont définis par les angles de rotation. Hamilton a présenté la forme composante de ces équations montrant que le produit de quaternions calcule le troisième sommet d'un triangle sphérique à partir de deux sommets donnés et de leurs longueurs d'arc associées, ce qui définit également une algèbre pour les points de la géométrie elliptique .

Composition de l'angle de l'axe

L'axe de rotation normalisé, en supprimant le du produit développé, laisse le vecteur qui est l'axe de rotation, fois un certain constant. Il faut veiller à normaliser le vecteur d'axe quand est ou où le vecteur est proche ; qui est l'identité, ou 0 rotation autour de n'importe quel axe. ${\displaystyle \cos {\frac {\gamma }{2}}}$${\style d'affichage \gamma }$${\style d'affichage 0}$${\displaystyle k2\pi }$${\style d'affichage 0}$

${\displaystyle \gamma =2\cos ^{-1}(\cos {\frac {\beta }{2}}\cos {\frac {\alpha }{2}}-\sin {\frac {\beta }{2}}\sin {\frac {\alpha }{2}}\mathbf {B} \cdot \mathbf {A} )}$

${\displaystyle \mathbf {D} ={\sin {\frac {\beta }{2}}\cos {\frac {\alpha }{2}}\mathbf {B} +\sin {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\mathbf {A} +\sin {\frac {\beta }{2}}\sin {\frac {\alpha }{2}} \mathbf {B} \times \mathbf {A} }}$

Ou avec des substitutions trigonométriques par addition d'angles ...

${\displaystyle \gamma =2\cos ^{-1}((1-\mathbf {A} \cdot \mathbf {B} )\cos {\frac {\beta -\alpha }{2}}+(1 +\mathbf {A} \cdot \mathbf {B} )\cos {\frac {\beta +\alpha }{2}})}$

${\displaystyle \mathbf {D} =({\sin {\frac {\beta +\alpha }{2}}+\sin {\frac {\beta -\alpha }{2}})\mathbf {A} +(\sin {\frac {\beta +\alpha }{2}}-\sin {\frac {\beta -\alpha }{2}})\mathbf {B} +(\cos {\frac {\ beta -\alpha }{2}}-\cos {\frac {\beta +\alpha }{2}})\mathbf {B} \times \mathbf {A} }}$

enfin normaliser l'axe de rotation : ou . ${\displaystyle {\frac {\mathbf {D} }{2\sin {\frac {\gamma }{2}}}}}$${\displaystyle {\frac {\mathbf {D} }{||\mathbf {D} ||}}}$

Différenciation par rapport au quaternion de rotation

Le quaternion tourné p' = q p q ^-1 doit être différencié par rapport au quaternion tournant q , lorsque la rotation est estimée à partir de l'optimisation numérique. L'estimation de l'angle de rotation est une procédure essentielle dans l'enregistrement d'objets 3D ou l'étalonnage d'une caméra. Pour q unitaire et p imaginaire pur , c'est-à-dire pour une rotation dans l'espace 3D, les dérivées du quaternion tourné peuvent être représentées en utilisant la notation du calcul matriciel comme

${\displaystyle {\begin{aligned}{\frac {\partial \mathbf {p'} }{\partial \mathbf {q} }}\equiv \left[{\frac {\partial \mathbf {p'} } {\partial q_{0}}},{\frac {\partial \mathbf {p'} }{\partial q_{x}}},{\frac {\partial \mathbf {p'} }{\partial q_ {y}}},{\frac {\partial \mathbf {p'} }{\partial q_{z}}}\right]=\left[\mathbf {pq} -(\mathbf {pq} )^{ *},(\mathbf {pqi} )^{*}-\mathbf {pqi} ,(\mathbf {pqj} )^{*}-\mathbf {pqj} ,(\mathbf {pqk} )^{*} -\mathbf {pqk} \right].\end{aligned}}}$

Une dérivation peut être trouvée dans.

Fond

quaternions

Les nombres complexes peuvent être définis en introduisant un symbole abstrait i qui satisfait les règles habituelles de l'algèbre et en plus la règle i ² = −1 . Cela suffit pour reproduire toutes les règles de l'arithmétique des nombres complexes : par exemple :

${\displaystyle (a+b\mathbf {i} )(c+d\mathbf {i} )=ac+ad\mathbf {i} +b\mathbf {i} c+b\mathbf {i} d\mathbf {i} =ac+ad\mathbf {i} +bc\mathbf {i} +bd\mathbf {i} ^{2}=(ac-bd)+(bc+ad)\mathbf {i} .}$

De la même manière les quaternions peuvent être définis en introduisant des symboles abstraits i , j , k qui satisfont les règles i ² = j ² = k ² = i j k = −1 et les règles algébriques usuelles sauf la loi commutative de multiplication (un exemple familier d'une telle multiplication non commutative est la multiplication matricielle ). De là découlent toutes les règles de l'arithmétique des quaternions, telles que les règles de multiplication des éléments de base des quaternions . En utilisant ces règles, on peut montrer que :

${\displaystyle (a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} )(e+f\mathbf {i} +g\mathbf {j} +h\mathbf {k} )=}$

${\displaystyle (ae-bf-cg-dh)+(af+be+ch-dg)\mathbf {i} +(ag-bh+ce+df)\mathbf {j} +(ah+bg-cf+ de)\mathbf {k} .}$

La partie imaginaire d'un se comporte de quaternions comme un vecteur à trois dimensions d' espace vectoriel , et la partie réelle a se comporte comme un scalaire dans R . Lorsque des quaternions sont utilisés en géométrie, il est plus pratique de les définir comme un scalaire plus un vecteur : ${\displaystyle b\mathbf {i} +c\mathbf {j} +d\mathbf {k} }$${\displaystyle {\vec {v}}=(b,c,d)}$

${\displaystyle a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} =a+{\vec {v}}.}$

Certains pourraient trouver étrange d'ajouter un nombre à un vecteur , car ce sont des objets de natures très différentes, ou de multiplier deux vecteurs ensemble, car cette opération est généralement indéfinie. Cependant, si l'on se souvient qu'il s'agit d'une simple notation pour les parties réelles et imaginaires d'un quaternion, cela devient plus légitime. En d'autres termes, le raisonnement correct est l'addition de deux quaternions, un avec zéro vecteur/partie imaginaire, et un autre avec zéro partie scalaire/réelle :

${\displaystyle q_{1}=s+{\vec {v}}=(s,{\vec {0}})+(0,{\vec {v}}).}$

Nous pouvons exprimer la multiplication de quaternions dans le langage moderne des produits vectoriels croisés et scalaires (qui ont en fait été inspirés par les quaternions en premier lieu). Lors de la multiplication du vecteur/parties imaginaires, à la place des règles i ² = j ² = k ² = ijk = −1, nous avons la règle de multiplication des quaternions :

${\displaystyle {\vec {v}}{\vec {w}}=-{\vec {v}}\cdot {\vec {w}}+{\vec {v}}\times {\vec {w }},}$

où:

• ${\displaystyle {\vec {v}}{\vec {w}}}$ est le quaternion résultant,
• ${\displaystyle {\vec {v}}\times {\vec {w}}}$ est le produit vectoriel vectoriel (un vecteur),
• ${\displaystyle {\vec {v}}\cdot {\vec {w}}}$ est un produit scalaire vectoriel (un scalaire).

La multiplication de quaternions est non commutative (à cause du produit croisé, qui anti-commute ), tandis que les multiplications scalaire-scalaire et scalaire-vecteur commutent. De ces règles il découle immédiatement que ( voir détails ) :

${\displaystyle q_{1}q_{2}=(s+{\vec {v}})(t+{\vec {w}})=(st-{\vec {v}}\cdot {\vec {w }})+(s{\vec {w}}+t{\vec {v}}+{\vec {v}}\times {\vec {w}}).}$

L'inverse multiplicatif (gauche et droite) ou réciproque d'un quaternion non nul est donné par le rapport conjugué-à-norme ( voir détails ):

${\displaystyle q_{1}^{-1}=(s+{\vec {v}})^{-1}={\frac {(s+{\vec {v}})^{*}}{\ lVert s+{\vec {v}}\rVert ^{2}}}={\frac {s-{\vec {v}}}{s^{2}+\lVert {\vec {v}}\rVert ^{2}}},}$

comme cela peut être vérifié par calcul direct (notez la similitude avec l' inverse multiplicatif des nombres complexes ).

Identité de rotation

Soit un vecteur unitaire (l'axe de rotation) et soit . Notre objectif est de montrer que ${\displaystyle {\vec {u}}}$${\displaystyle q=\cos {\frac {\alpha }{2}}+{\vec {u}}\sin {\frac {\alpha }{2}}}$

${\displaystyle {\vec {v'}}=q{\vec {v}}q^{-1}=\left(\cos {\frac {\alpha }{2}}+{\vec {u} }\sin {\frac {\alpha }{2}}\right)\,{\vec {v}}\,\left(\cos {\frac {\alpha }{2}}-{\vec {u }}\sin {\frac {\alpha }{2}}\right)}$

donne le vecteur tourné d'un angle autour de l'axe . En élargissant (et en gardant à l'esprit que ), nous avons ${\displaystyle {\vec {v}}}$${\style d'affichage \alpha }$${\displaystyle {\vec {u}}}$${\displaystyle {\vec {u}}{\vec {v}}={\vec {u}}\times {\vec {v}}-{\vec {u}}\cdot {\vec {v} }}$

${\displaystyle {\begin{aligned}{\vec {v}}'&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+({\vec {u }}{\vec {v}}-{\vec {v}}{\vec {u}})\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2} }-{\vec {u}}{\vec {v}}{\vec {u}}\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2({\vec {u}}\times {\vec {v}})\sin {\frac {\alpha } {2}}\cos {\frac {\alpha }{2}}-(({\vec {u}}\times {\vec {v}})-({\vec {u}}\cdot {\ vec {v}})){\vec {u}}\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}\cos ^{2 }{\frac {\alpha }{2}}+2({\vec {u}}\times {\vec {v}})\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-(({\vec {u}}\times {\vec {v}}){\vec {u}}-({\vec {u}}\cdot {\vec { v}}){\vec {u}})\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}\cos ^{2}{ \frac {\alpha }{2}}+2({\vec {u}}\times {\vec {v}})\sin {\frac {\alpha }{2}}\cos {\frac {\ alpha }{2}}-((({\vec {u}}\times {\vec {v}})\times {\vec {u}}-({\vec {u}}\times {\vec {v}})\cdot {\vec {u}})-({\vec {u}}\cdot {\vec {v}}){\vec {u}})\sin ^{2}{\ frac {\alpha }{2}}\ \[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2({\vec {u}}\times {\vec {v}}) \sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-(({\vec {v}}-({\vec {u}}\cdot {\vec {v}}){\vec {u}})-0-({\vec {u}}\cdot {\vec {v}}){\vec {u}})\sin ^{2}{\ frac {\alpha }{2}}\\[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2({\vec {u}} \times {\vec {v}})\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-({\vec {v}}-2{\vec {u}}({\vec {u}}\cdot {\vec {v}}))\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2({\vec {u}}\times {\vec {v}})\sin {\frac {\alpha } {2}}\cos {\frac {\alpha }{2}}-{\vec {v}}\sin ^{2}{\frac {\alpha }{2}}+2{\vec {u} }({\vec {u}}\cdot {\vec {v}})\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}} (\cos ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\alpha }{2}})+({\vec {u}}\times {\ vec {v}})(2\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}})+{\vec {u}}({\vec {u} }\cdot {\vec {v}})(2\sin ^{2}{\frac {\alpha }{2}})\\[6pt]\end{aligned}}}$

Utilisation des identités trigonométriques :

${\displaystyle {\begin{aligned}{\vec {v}}'&={\vec {v}}(\cos ^{2}{\frac {\alpha }{2}}-\sin ^{2 }{\frac {\alpha }{2}})+({\vec {u}}\times {\vec {v}})(2\sin {\frac {\alpha }{2}}\cos { \frac {\alpha }{2}})+{\vec {u}}({\vec {u}}\cdot {\vec {v}})(2\sin ^{2}{\frac {\ alpha }{2}})\\[6pt]&={\vec {v}}\cos \alpha +({\vec {u}}\times {\vec {v}})\sin \alpha +{ \vec {u}}({\vec {u}}\cdot {\vec {v}})(1-\cos \alpha )\\[6pt]&={\vec {v}}\cos \alpha +({\vec {u}}\times {\vec {v}})\sin \alpha +{\vec {u}}({\vec {u}}\cdot {\vec {v}})- {\vec {u}}({\vec {u}}\cdot {\vec {v}})\cos \alpha \\[6pt]&=({\vec {v}}-{\vec {u }}({\vec {u}}\cdot {\vec {v}}))\cos \alpha +({\vec {u}}\times {\vec {v}})\sin \alpha +{ \vec {u}}({\vec {u}}\cdot {\vec {v}})\\[6pt]&={\vec {v}}_{\bot }\cos \alpha +({ \vec {u}}\times {\vec {v}})\sin \alpha +{\vec {v}}_{\|}\end{aligned}}}$

où et sont les composantes de v → (respectivement perpendiculaire et parallèle à u → ). C'est la formule d'une rotation par autour de l' axe u → . ${\displaystyle {\vec {v}}_{\bot }}$${\displaystyle {\vec {v}}_{\|}}$${\style d'affichage \alpha }$

Opérations de rotation des quaternions

Une explication très formelle des propriétés utilisées dans cette section est donnée par Altman.

L'hypersphère des rotations

Visualiser l'espace des rotations

Les quaternions unitaires représentent le groupe des rotations euclidiennes en trois dimensions d'une manière très simple. La correspondance entre les rotations et les quaternions peut être comprise en visualisant d'abord l'espace des rotations lui-même.

Afin de visualiser l'espace des rotations, il est utile de considérer un cas plus simple. Toute rotation en trois dimensions peut être décrite par une rotation d'un certain angle autour d'un certain axe ; pour nos besoins, nous utiliserons un vecteur d' axe pour établir la latéralité de notre angle. Considérons le cas particulier dans lequel l'axe de rotation se trouve dans le plan xy . On peut alors spécifier l'axe de l'une de ces rotations par un point d'un cercle traversé par le vecteur, et on peut sélectionner le rayon du cercle pour désigner l' angle de rotation .

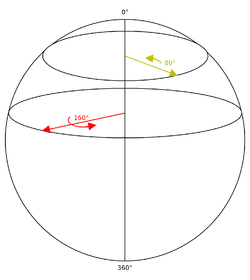
De même, une rotation dont l'axe de rotation se situe dans le plan xy peut être décrite comme un point sur une sphère de rayon fixe en trois dimensions. En commençant au pôle nord d'une sphère dans l'espace tridimensionnel, nous spécifions le point au pôle nord comme étant la rotation d'identité (une rotation à angle nul). Tout comme dans le cas de la rotation identité, aucun axe de rotation n'est défini, et l'angle de rotation (zéro) n'a pas d'importance. Une rotation ayant un très petit angle de rotation peut être spécifiée par une coupe à travers la sphère parallèle au plan xy et très près du pôle nord. Le cercle défini par cette tranche sera très petit, correspondant au petit angle de rotation. Au fur et à mesure que les angles de rotation deviennent plus grands, la tranche se déplace dans la direction z négative et les cercles deviennent plus grands jusqu'à ce que l'équateur de la sphère soit atteint, ce qui correspondra à un angle de rotation de 180 degrés. En continuant vers le sud, les rayons des cercles deviennent maintenant plus petits (correspondant à la valeur absolue de l'angle de rotation considéré comme un nombre négatif). Enfin, lorsque le pôle sud est atteint, les cercles se rétrécissent à nouveau jusqu'à la rotation d'identité, qui est également spécifiée comme le point au pôle sud.

Notez qu'un certain nombre de caractéristiques de telles rotations et de leurs représentations peuvent être vues par cette visualisation. L'espace des rotations est continu, chaque rotation a un voisinage de rotations qui sont à peu près les mêmes, et ce voisinage devient plat au fur et à mesure que le voisinage se rétrécit. De plus, chaque rotation est en fait représentée par deux points antipodaux sur la sphère, qui se trouvent aux extrémités opposées d'une ligne passant par le centre de la sphère. Cela reflète le fait que chaque rotation peut être représentée comme une rotation autour d'un axe, ou, de manière équivalente, comme une rotation négative autour d'un axe pointant dans la direction opposée (une soi-disant double couverture ). La "latitude" d'un cercle représentant un angle de rotation particulier sera la moitié de l'angle représenté par cette rotation, car lorsque le point est déplacé du pôle nord au pôle sud, la latitude varie de zéro à 180 degrés, tandis que l'angle de rotation varie de 0 à 360 degrés. (la "longitude" d'un point représente alors un axe de rotation particulier.) Notez cependant que cet ensemble de rotations n'est pas fermé sous composition. Deux rotations successives avec des axes dans le plan xy ne donneront pas nécessairement une rotation dont l'axe se situe dans le plan xy , et ne peuvent donc pas être représentées comme un point sur la sphère. Ce ne sera pas le cas avec une rotation générale en 3-espace, dans laquelle les rotations forment un ensemble fermé sous composition.

Cette visualisation peut être étendue à une rotation générale dans l'espace tridimensionnel. La rotation d'identité est un point, et un petit angle de rotation autour d'un axe peut être représenté comme un point sur une sphère avec un petit rayon. Au fur et à mesure que l'angle de rotation grandit, la sphère grandit jusqu'à ce que l'angle de rotation atteigne 180 degrés, point auquel la sphère commence à se rétrécir, devenant un point à mesure que l'angle approche de 360 ​​degrés (ou zéro degré par rapport à la direction négative). Cet ensemble de sphères en expansion et en contraction représente une hypersphère dans un espace à quatre dimensions (une 3-sphère). Tout comme dans l'exemple plus simple ci-dessus, chaque rotation représentée comme un point sur l'hypersphère correspond à son point antipodal sur cette hypersphère. La "latitude" sur l'hypersphère sera la moitié de l'angle de rotation correspondant, et le voisinage de tout point deviendra "plus plat" (c'est-à-dire représenté par un espace euclidien 3-D de points) à mesure que le voisinage se rétrécit. Ce comportement correspond à l'ensemble des quaternions unitaires : Un quaternion général représente un point dans un espace à quatre dimensions, mais le contraindre à avoir une magnitude unitaire donne un espace à trois dimensions équivalent à la surface d'une hypersphère. La magnitude du quaternion unitaire sera l'unité, correspondant à une hypersphère de rayon unitaire. La partie vectorielle d'un quaternion unitaire représente le rayon de la 2-sphère correspondant à l'axe de rotation, et sa grandeur est le cosinus de la moitié de l'angle de rotation. Chaque rotation est représentée par deux quaternions unitaires de signe opposé, et, comme dans l'espace des rotations en trois dimensions, le produit de quaternions de deux quaternions unitaires donnera un quaternion unitaire. De plus, l'espace des quaternions unitaires est « plat » dans tout voisinage infinitésimal d'un quaternion unitaire donné.

Paramétrage de l'espace de rotations

Nous pouvons paramétrer la surface d'une sphère avec deux coordonnées, telles que la latitude et la longitude. Mais la latitude et la longitude se comportent mal ( dégénérées ) aux pôles nord et sud, bien que les pôles ne soient pas intrinsèquement différents des autres points de la sphère. Aux pôles (latitudes +90° et -90°), la longitude n'a plus de sens.

On peut montrer qu'aucun système de coordonnées à deux paramètres ne peut éviter une telle dégénérescence. Nous pouvons éviter de tels problèmes en plongeant la sphère dans l'espace tridimensionnel et en la paramétrant avec trois coordonnées cartésiennes ( w ,  x ,  y ) , en plaçant le pôle nord à ( w ,  x ,  y ) = (1, 0, 0) , le pôle sud à ( w ,  x ,  y ) = (−1, 0, 0) , et l'équateur à w = 0 , x ² + y ² = 1 . Les points sur la sphère satisfont à la contrainte w ² + x ² + y ² = 1 , nous n'avons donc toujours que deux degrés de liberté bien qu'il y ait trois coordonnées. Un point ( w ,  x ,  y ) sur la sphère représente une rotation dans l' espace ordinaire autour de l' axe horizontal dirigé par le vecteur ( x ,  y , 0) d' un angle . ${\displaystyle \alpha =2\cos ^{-1}w=2\sin ^{-1}{\sqrt {x^{2}+y^{2}}}}$

De la même manière, l'espace hypersphérique des rotations 3D peut être paramétré par trois angles ( angles d' Euler ), mais toute paramétrisation de ce type est dégénérée en certains points de l'hypersphère, conduisant au problème de blocage du cardan . Nous pouvons éviter cela en utilisant quatre coordonnées euclidiennes w ,  x ,  y ,  z , avec w ² + x ² + y ² + z ² = 1 . Le point ( w ,  x ,  y ,  z ) représente une rotation autour de l' axe dirigé par le vecteur ( x ,  y ,  z ) d' un angle${\displaystyle \alpha =2\cos ^{-1}w=2\sin ^{-1}{\sqrt {x^{2}+y^{2}+z^{2}}}.}$

Expliquer les propriétés des quaternions avec des rotations

Non-commutativité

La multiplication des quaternions est non commutative . Ce fait explique comment la formule p ↦ q p q ⁻¹ peut fonctionner, ayant q q ⁻¹ = 1 par définition. Puisque la multiplication des quaternions unitaires correspond à la composition des rotations tridimensionnelles, cette propriété peut être rendue intuitive en montrant que les rotations tridimensionnelles ne sont pas commutatives en général.

Placez deux livres l'un à côté de l'autre. Faites pivoter l'un d'eux de 90 degrés dans le sens des aiguilles d'une montre autour de l' axe z , puis de 180 degrés autour de l' axe x . Prenez l'autre livre, retournez-le d'abord à 180° autour de l' axe x , puis à 90° dans le sens des aiguilles d'une montre autour de z . Les deux livres ne finissent pas parallèles. Cela montre qu'en général, la composition de deux rotations différentes autour de deux axes spatiaux distincts ne commutera pas.

Orientation

Le produit vectoriel vectoriel , utilisé pour définir la représentation axe-angle, confère une orientation (« latéralité ») à l'espace : dans un espace vectoriel tridimensionnel, les trois vecteurs de l'équation a  ×  b = c formeront toujours un droit -ensemble main gauche (ou un ensemble main gauche, selon la façon dont le produit vectoriel est défini), fixant ainsi une orientation dans l'espace vectoriel. Alternativement, la dépendance à l'orientation est exprimée en se référant à un tel u → qui spécifie une rotation quant aux vecteurs axiaux . Dans le formalisme quaternionique le choix d'une orientation de l'espace correspond à l'ordre de multiplication : ij = k mais ji = − k . Si on inverse l'orientation, alors la formule ci-dessus devient p ↦ q ⁻¹  p q , c'est-à-dire qu'une unité q est remplacée par le quaternion conjugué – le même comportement que les vecteurs axiaux.

Conventions alternatives

Il est rapporté que l'existence et l'utilisation continue d'une convention de quaternion alternative dans la communauté aérospatiale et, dans une moindre mesure, la communauté robotique encourent un coût important et permanent [ sic ]. Cette convention alternative est proposée par Shuster MD dans et s'écarte de la tradition en inversant la définition pour multiplier les éléments de base de quaternions tels que sous la convention de Shuster, alors que la définition de Hamilton est . ${\displaystyle \mathbf {i} \mathbf {j} =-\mathbf {k} }$${\displaystyle \mathbf {i} \mathbf {j} =\mathbf {k} }$

Selon la convention de Shuster, la formule de multiplication de deux quaternions est modifiée de telle sorte que

${\displaystyle (r_{1},\ {\vec {v}}_{1})(r_{2},\ {\vec {v}}_{2})=(r_{1}r_{2 }-{\vec {v}}_{1}\cdot {\vec {v}}_{2},\ r_{1}{\vec {v}}_{2}+r_{2}{\ vec {v}}_{1}\color {red}\mathbf {-} \color {black}{\vec {v}}_{1}\times {\vec {v}}_{2}), }$

La formule pour faire tourner un vecteur par un quaternion est modifiée pour être

${\displaystyle {\begin{aligned}\mathbf {p} '_{alt}=&\ (\mathbf {v} \otimes \mathbf {v} +q_{r}^{2}\mathbf {I} \ ,\color {rouge}\mathbf {-} \,\color {noir}2q_{r}[\mathbf {v} ]_{\times }+[\mathbf {v} ]_{\times }^{2 })\mathbf {p} \\=&\ (\mathbf {I} \,\color {rouge}\mathbf {-} \,\color {noir}2q_{r}[\mathbf {v} ]_{ \times }+2[\mathbf {v} ]_{\times }^{2})\mathbf {p} \end{aligned}}}$

Pour identifier les changements selon la convention de Shuster, vérifiez que le signe avant le produit croisé est inversé de plus à moins.

Enfin, la formule de conversion d'un quaternion en matrice de rotation est modifiée pour être

${\displaystyle {\begin{aligned}\mathbf {R} _{alt}&=\ \mathbf {I} \,\color {red}\mathbf {-} \,\color {black}2q_{r}[ \mathbf {v} ]_{\times }+2[\mathbf {v} ]_{\times }^{2})\\&={\begin{bmatrix}1-2s(q_{j}^{ 2}+q_{k}^{2})&2(q_{i}q_{j}+q_{k}q_{r})&2(q_{i}q_{k}-q_{j}q_{r })\\2(q_{i}q_{j}-q_{k}q_{r})&1-2s(q_{i}^{2}+q_{k}^{2})&2(q_{ j}q_{k}+q_{i}q_{r})\\2(q_{i}q_{k}+q_{j}q_{r})&2(q_{j}q_{k}-q_ {i}q_{r})&1-2s(q_{i}^{2}+q_{j}^{2})\end{bmatrix}}\end{aligned}}}$

qui est exactement la transposée de la matrice de rotation convertie selon la convention traditionnelle.

Le tableau ci-dessous regroupe les demandes selon leur adhésion à l'une ou l'autre convention de quaternions

Applications logicielles par convention utilisée

Convention de multiplication de Hamilton	Convention de multiplication de Shuster
Wolfram Mathematica Boîte à outils du système robotique MATLAB Boîte à outils MATLAB Aerospace ROS propre Booster les quaternions Quaternion.js Solveur de Cérès	* Bibliothèque mathématique Microsoft DirectX

Bien que l'utilisation de l'une ou l'autre convention n'affecte pas la capacité ou l'exactitude des applications ainsi créées, les auteurs de ont fait valoir que la convention de Shuster devrait être abandonnée car elle s'écarte de la convention de multiplication de quaternions beaucoup plus ancienne de Hamilton et pourrait ne jamais être adoptée par la théorie mathématique ou théorique. domaines de la physique.

Comparaison avec d'autres représentations des rotations

Avantages des quaternions

La représentation d'une rotation sous forme de quaternion (4 nombres) est plus compacte que la représentation sous forme de matrice orthogonale (9 nombres). De plus, pour un axe et un angle donnés, on peut facilement construire le quaternion correspondant, et inversement, pour un quaternion donné on peut facilement lire l'axe et l'angle. Les deux sont beaucoup plus difficiles avec des matrices ou des angles d'Euler .

Dans les jeux vidéo et autres applications, on s'intéresse souvent aux "rotations douces", ce qui signifie que la scène doit tourner lentement et non en une seule étape. Ceci peut être accompli en choisissant une courbe telle que l' interpolation linéaire sphérique dans les quaternions, avec un point final étant la transformation d'identité 1 (ou une autre rotation initiale) et l'autre étant la rotation finale prévue. Ceci est plus problématique avec d'autres représentations des rotations.

Lorsqu'on compose plusieurs rotations sur un ordinateur, les erreurs d'arrondi s'accumulent forcément. Un quaternion légèrement décalé représente toujours une rotation après avoir été normalisé : une matrice légèrement décalée peut ne plus être orthogonale et est plus difficile à reconvertir en une matrice orthogonale appropriée.

Les quaternions évitent également un phénomène appelé blocage du cardan qui peut se produire lorsque, par exemple dans les systèmes de rotation tangage/lacet/roulis , le tangage est tourné de 90° vers le haut ou vers le bas, de sorte que le lacet et le roulis correspondent alors au même mouvement, et à un degré de la liberté de rotation est perdue. Dans un système de navigation inertielle aérospatiale basé sur un cardan , par exemple, cela pourrait avoir des résultats désastreux si l'avion est en piqué ou en montée raide.

Conversion vers et depuis la représentation matricielle

D'un quaternion à une matrice orthogonale

La matrice orthogonale correspondant à une rotation par le quaternion unité z = a + b  i + c  j + d  k (avec | z | = 1   ) en post-multipliant avec un vecteur colonne est donnée par

${\displaystyle R={\begin{pmatrix}a^{2}+b^{2}-c^{2}-d^{2}&2bc-2ad&2bd+2ac\\2bc+2ad&a^{2}-b ^{2}+c^{2}-d^{2}&2cd-2ab\\2bd-2ac&2cd+2ab&a^{2}-b^{2}-c^{2}+d^{2}\\ \end{pmatrix}}.}$

Cette matrice de rotation est utilisée sur le vecteur w as . La représentation en quaternion de cette rotation est donnée par : ${\displaystyle w_{rotation}=R\cdot w}$

${\displaystyle {\begin{bmatrix}0\\w_{rotation}\end{bmatrix}}=z{\begin{bmatrix}0\\w\end{bmatrix}}z^{*},}$

où est le conjugué du quaternion , donné par${\displaystyle z^{*}}$${\style d'affichage z}$${\displaystyle \mathbf {z} ^{*}=ab\mathbf {i} -c\mathbf {j} -d\mathbf {k} }$

De plus, la multiplication de quaternions est définie comme (en supposant que a et b sont des quaternions, comme z ci-dessus) :

${\displaystyle ab=(a_{0}b_{0}-{\vec {a}}\cdot {\vec {b}};a_{0}{\vec {b}}+b_{0}{\ vec {a}}+{\vec {a}}\times {\vec {b}})}$

où l'ordre a , b est important puisque le produit vectoriel de deux vecteurs n'est pas commutatif.

D'une matrice orthogonale à un quaternion

Il faut être prudent lors de la conversion d'une matrice de rotation en quaternion, car plusieurs méthodes simples ont tendance à être instables lorsque la trace (somme des éléments diagonaux) de la matrice de rotation est nulle ou très petite. Pour une méthode stable de conversion d'une matrice orthogonale en quaternion, consultez la sous-section Quaternion de l' article Matrice de rotation .

Quaternions d'ajustement

La section ci-dessus décrit comment récupérer un quaternion q à partir d'une matrice de rotation 3 × 3 Q . Supposons, cependant, que nous ayons une matrice Q qui ne soit pas une rotation pure - en raison d' erreurs d'arrondi , par exemple - et que nous souhaitions trouver le quaternion q qui représente le plus précisément Q . Dans ce cas, nous construisons une matrice symétrique 4 × 4

${\displaystyle K={\frac {1}{3}}{\begin{bmatrix}Q_{xx}-Q_{yy}-Q_{zz}&Q_{yx}+Q_{xy}&Q_{zx}+Q_ {xz}&Q_{zy}-Q_{yz}\\Q_{yx}+Q_{xy}&Q_{yy}-Q_{xx}-Q_{zz}&Q_{zy}+Q_{yz}&Q_{xz} -Q_{zx}\\Q_{zx}+Q_{xz}&Q_{zy}+Q_{yz}&Q_{zz}-Q_{xx}-Q_{yy}&Q_{yx}-Q_{xy}\\ Q_{zy}-Q_{yz}&Q_{xz}-Q_{zx}&Q_{yx}-Q_{xy}&Q_{xx}+Q_{yy}+Q_{zz}\end{bmatrix}},}$

et trouver le vecteur propre ( x ,  y ,  z ,  w ) correspondant à la plus grande valeur propre (cette valeur sera 1 si et seulement si Q est une rotation pure). Le quaternion ainsi obtenu correspondra à la rotation la plus proche de la matrice d'origine Q .

Comparaisons de performances

Cette section traite des implications en termes de performances de l'utilisation de quaternions par rapport à d'autres méthodes (axes/angles ou matrices de rotation) pour effectuer des rotations en 3D.

Résultats

Exigences de stockage

Méthode	Espace de rangement
Matrice de rotation	9
quaternion	3 ou 4 (voir ci-dessous)
Angle/axe	3 ou 4 (voir ci-dessous)

Seuls trois des composants du quaternion sont indépendants, car une rotation est représentée par un quaternion unitaire. Pour un calcul ultérieur, on a généralement besoin des quatre éléments, de sorte que tous les calculs subiraient des dépenses supplémentaires du fait de la récupération du quatrième composant. De même, l'angle/l'axe peut être stocké dans un vecteur à trois composantes en multipliant la direction de l'unité par l'angle (ou une fonction de celui-ci), mais cela entraîne un coût de calcul supplémentaire lors de son utilisation pour les calculs.

Comparaison des performances des opérations de chaînage de rotation

Méthode	# multiplie	# additions/soustraits	opérations totales
Matrices de rotation	27	18	45
quaternions	16	12	28

Comparaison des performances des opérations de rotation vectorielle

Méthode		# multiplie	# additions/soustraits	# péché/cos	opérations totales
Matrice de rotation		9	6	0	15
Quaternions *	Sans matrice intermédiaire	15	15	0	30
Quaternions *	Avec matrice intermédiaire	21	18	0	39
Angle/axe	Sans matrice intermédiaire	18	13	2	30 + 3
Angle/axe	Avec matrice intermédiaire	21	16	2	37 + 2

* Remarque : Les quaternions peuvent être implicitement convertis en une matrice de type rotation (12 multiplications et 12 additions/soustractions), qui nivelle le coût de rotation des vecteurs suivants avec la méthode de la matrice de rotation.

Méthodes utilisées

Il existe trois approches de base pour faire tourner un vecteur v → :

1. Calculer le produit matriciel d'une matrice de rotation 3 × 3 R et de la matrice colonne originale 3 × 1 représentant v → . Cela nécessite 3 × (3 multiplications + 2 additions) = 9 multiplications et 6 additions, la méthode la plus efficace pour faire tourner un vecteur.
2. Une rotation peut être représentée par un quaternion de longueur unitaire q = ( w ,  r → ) avec une partie scalaire (réelle) w et une partie vectorielle (imaginaire) r → . La rotation peut être appliquée à un vecteur 3D v → via la formule . Cela ne nécessite que 15 multiplications et 15 additions à évaluer (ou 18 multiplications et 12 additions si le facteur de 2 est fait via la multiplication.) Cette formule, initialement pensée pour être utilisée avec la notation axe/angle (formule de Rodrigues), peut également être appliqué à la notation des quaternions. Cela donne le même résultat que la formule moins efficace mais plus compacte de la multiplication des quaternions .${\displaystyle {\vec {v}}_{\text{new}}={\vec {v}}+2{\vec {r}}\times ({\vec {r}}\times {\vec {v}}+w{\vec {v}})}$${\displaystyle {\vec {v}}_{\text{new}}=q{\vec {v}}q^{-1}}$
3. Utilisez la formule angle/axe pour convertir un angle/axe en une matrice de rotation R puis en multipliant avec un vecteur, ou, de la même manière, utilisez une formule pour convertir la notation quaternion en une matrice de rotation, puis en multipliant avec un vecteur. La conversion de l'angle/axe en R coûte 12 multiplications, 2 appels de fonction (sin, cos) et 10 additions/soustractions ; à partir de l'élément 1, la rotation à l'aide de R ajoute 9 multiplications et 6 additions supplémentaires pour un total de 21 multiplications, 16 additions/soustractions et 2 appels de fonction (sin, cos). La conversion d'un quaternion en R coûte 12 multiplications et 12 additions/soustractions ; à partir de l'item 1, la rotation à l'aide de R ajoute 9 multiplications et 6 additions supplémentaires pour un total de 21 multiplications et 18 additions/soustractions.

Comparaison des performances de n opérations de rotation vectorielles

Méthode		# multiplie	# additions/soustraits	# péché/cos	opérations totales
Matrice de rotation		9 n	6 n	0	15 n
Quaternions *	Sans matrice intermédiaire	15 n	15 n	0	30 n
Quaternions *	Avec matrice intermédiaire	9 n + 12	6 n + 12	0	15 n + 24
Angle/axe	Sans matrice intermédiaire	18 n	12 n + 1	2	30 n + 3
Angle/axe	Avec matrice intermédiaire	9 n + 12	6 n + 10	2	15 n + 24

Paires de quaternions unitaires sous forme de rotations dans l'espace 4D

Une paire de quaternions unitaires z _l et z _r peut représenter n'importe quelle rotation dans l'espace 4D . Étant donné un vecteur à quatre dimensions v → , et en supposant qu'il s'agit d'un quaternion, nous pouvons faire pivoter le vecteur v → comme ceci :

${\displaystyle f({\vec {v}})=\mathbf {z} _{\rm {l}}{\vec {v}}\mathbf {z} _{\rm {r}}={\ begin{pmatrix}a_{\rm {l}}&-b_{\rm {l}}&-c_{\rm {l}}&-d_{\rm {l}}\\b_{\rm {l }}&a_{\rm {l}}&-d_{\rm {l}}&c_{\rm {l}}\\c_{\rm {l}}&d_{\rm {l}}&a_{\rm {l}}&-b_{\rm {l}}\\d_{\rm {l}}&-c_{\rm {l}}&b_{\rm {l}}&a_{\rm {l}} \end{pmatrix}}{\begin{pmatrix}w\\x\\y\\z\end{pmatrix}}{\begin{pmatrix}a_{\rm {r}}&-b_{\rm {r }}&-c_{\rm {r}}&-d_{\rm {r}}\\b_{\rm {r}}&a_{\rm {r}}&d_{\rm {r}}&- c_{\rm {r}}\\c_{\rm {r}}&-d_{\rm {r}}&a_{\rm {r}}&b_{\rm {r}}\\d_{\rm {r}}&c_{\rm {r}}&-b_{\rm {r}}&a_{\rm {r}}\end{pmatrix}}.}$

La paire de matrices représente une rotation de ⁴ . Notez que depuis , les deux matrices doivent commuter. Par conséquent, il existe deux sous - groupes de navettage du groupe des rotations à quatre dimensions. Les rotations arbitraires à quatre dimensions ont 6 degrés de liberté ; chaque matrice représente 3 de ces 6 degrés de liberté. ${\displaystyle (\mathbf {z} _{\rm {l}}{\vec {v}})\mathbf {z} _{\rm {r}}=\mathbf {z} _{\rm {l }}({\vec {v}}\mathbf {z} _{\rm {r}})}$

Puisque les générateurs des rotations à quatre dimensions peuvent être représentés par des paires de quaternions (comme suit), toutes les rotations à quatre dimensions peuvent également être représentées.

${\displaystyle \mathbf {z} _{\rm {l}}{\vec {v}}\mathbf {z} _{\rm {r}}={\begin{pmatrix}1&-dt_{ab}& -dt_{ac}&-dt_{ad}\\dt_{ab}&1&-dt_{bc}&-dt_{bd}\\dt_{ac}&dt_{bc}&1&-dt_{cd}\\dt_{ad }&dt_{bd}&dt_{cd}&1\end{pmatrix}}{\begin{pmatrix}w\\x\\y\\z\end{pmatrix}}}$

${\displaystyle \mathbf {z} _{\rm {l}}=1+{dt_{ab}+dt_{cd} \over 2}i+{dt_{ac}-dt_{bd} \over 2}j+{ dt_{ad}+dt_{bc} \over 2}k}$

${\displaystyle \mathbf {z} _{\rm {r}}=1+{dt_{ab}-dt_{cd} \over 2}i+{dt_{ac}+dt_{bd} \over 2}j+{ dt_{ad}-dt_{bc} \over 2}k}$

Voir également

Les références

Lectures complémentaires

• Grubin, Carl (1970). « Dérivation du schéma de quaternion via l'axe et l'angle d'Euler ». Journal des vaisseaux spatiaux et des fusées . 7 (10) : 1261-1263. Bibcode : 1970JSpRo ... 7.1261G . doi : 10.2514/3.30149 .
• Battey-Pratt, EP ; Racey, TJ (1980). "Modèle géométrique pour les particules fondamentales". Journal international de physique théorique . 19 (6) : 437-475. Bibcode : 1980IJTP ... 19..437B . doi : 10.1007/BF00671608 . S2CID  120642923 .

• Arribas, M. ; Elie, A.; Palacios, M. (2006). « Les quaternions et les rotations d'un corps rigide ». Céleste. Méca. Dyna. Astron . 96 (3-4): 239-251. Bibcode : 2006CeMDA..96..239A . doi : 10.1007/s10569-006-9037-6 . S2CID  123591599 .

Liens externes et ressources

• Cordonnier, Ken. "Quaternions" (PDF) .
• "Type Quaternion simple et opérations dans plus de trente langages informatiques" .sur Rosetta Code
• Hart, John C. "Démonstrateur de quaternion" .
• Barrage, Eik B.; Koch, Martin; Lillholm, Martin (1998). "Quaternions, Interpolation et Animation" (PDF) .
• Léandra, Vicci (2001). "Quaternions et rotations dans 3-Space: L'algèbre et son interprétation géométrique" (PDF) .
• Howell, Thomas ; Lafon, Jean-Claude (1975). « La complexité du produit Quaternion, TR75-245 » (PDF) . L'Université de Cornell.
• Horn, Berthold KP (2001). "Quelques notes sur les quaternions unitaires et la rotation" (PDF) .
• Lee, Byung-Uk (1991). Unité Quaternion Représentation de la rotation - Annexe A, Différenciation avec les quaternions - Annexe B (PDF) (Thèse de doctorat). Université de Stanford.
• Vance, Rod. "Quelques exemples de groupes de Lie connectés" .
• "Représentation visuelle de la rotation des quaternions" .