Espace-temps -Spacetime
| Partie d'une série sur |
| Espace-temps |
|---|
 |
En physique , l'espace -temps est un modèle mathématique qui combine les trois dimensions de l'espace et une dimension du temps en une seule variété à quatre dimensions . Les diagrammes d'espace -temps peuvent être utilisés pour visualiser les effets relativistes , par exemple pourquoi différents observateurs perçoivent différemment où et quand les événements se produisent.
Jusqu'au XXe siècle, on supposait que la géométrie tridimensionnelle de l'univers (son expression spatiale en termes de coordonnées, de distances et de directions) était indépendante du temps unidimensionnel. Le physicien Albert Einstein a aidé à développer l'idée de l'espace-temps dans le cadre de sa théorie de la relativité . Avant son travail de pionnier, les scientifiques avaient deux théories distinctes pour expliquer les phénomènes physiques : les lois de la physique d' Isaac Newton décrivaient le mouvement d'objets massifs, tandis que les modèles électromagnétiques de James Clerk Maxwell expliquaient les propriétés de la lumière. Cependant, en 1905, Einstein fonde un travail sur la relativité restreinte sur deux postulats :
- Les lois de la physique sont invariantes (c'est-à-dire identiques) dans tous les systèmes inertiels (c'est-à-dire des référentiels non accélérés)
- La vitesse de la lumière dans le vide est la même pour tous les observateurs, quel que soit le mouvement de la source lumineuse.
La conséquence logique de la réunion de ces postulats est l'union inséparable des quatre dimensions, supposées jusqu'alors indépendantes, de l'espace et du temps. De nombreuses conséquences contre-intuitives émergent : en plus d'être indépendante du mouvement de la source lumineuse, la vitesse de la lumière est constante quel que soit le référentiel dans lequel elle est mesurée ; les distances et même l'ordre temporel des paires d'événements changent lorsqu'ils sont mesurés dans différents référentiels inertiels (c'est la relativité de la simultanéité ); et l'additivité linéaire des vitesses n'est plus vraie.
Einstein a formulé sa théorie en termes de cinématique (l'étude des corps en mouvement). Sa théorie était une avancée par rapport à la théorie des phénomènes électromagnétiques de Lorentz en 1904 et à la théorie électrodynamique de Poincaré . Bien que ces théories incluaient des équations identiques à celles introduites par Einstein ( c . paradigmes existants.
En 1908, Hermann Minkowski - autrefois l'un des professeurs de mathématiques d'un jeune Einstein à Zurich - a présenté une interprétation géométrique de la relativité restreinte qui fusionnait le temps et les trois dimensions spatiales de l'espace en un seul continuum à quatre dimensions maintenant connu sous le nom d' espace de Minkowski . Une caractéristique clé de cette interprétation est la définition formelle de l'intervalle d'espace-temps. Bien que les mesures de distance et de temps entre les événements diffèrent pour les mesures effectuées dans des référentiels différents, l'intervalle spatio-temporel est indépendant du référentiel inertiel dans lequel ils sont enregistrés.
L'interprétation géométrique de la relativité de Minkowski devait s'avérer vitale pour le développement par Einstein de sa théorie générale de la relativité de 1915 , dans laquelle il montrait comment la masse et l'énergie courbent l'espace-temps plat en une variété pseudo-riemannienne .
Introduction
Définitions
La mécanique classique non relativiste traite le temps comme une quantité de mesure universelle qui est uniforme dans tout l'espace et séparée de l'espace. La mécanique classique suppose que le temps a un taux de passage constant, indépendant de l' état de mouvement de l' observateur ou de tout élément externe. De plus, il suppose que l'espace est euclidien ; il suppose que l'espace suit la géométrie du sens commun.
Dans le contexte de la relativité restreinte , le temps ne peut être séparé des trois dimensions de l'espace, car la vitesse observée à laquelle le temps passe pour un objet dépend de la vitesse de l'objet par rapport à l'observateur. La relativité générale fournit également une explication de la façon dont les champs gravitationnels peuvent ralentir le passage du temps pour un objet tel qu'il est vu par un observateur extérieur au champ.
Dans l'espace ordinaire, une position est spécifiée par trois nombres, appelés dimensions . Dans le système de coordonnées cartésiennes , celles-ci sont appelées x, y et z. Une position dans l'espace-temps est appelée un événement et nécessite la spécification de quatre nombres : l'emplacement tridimensionnel dans l'espace, plus la position dans le temps (Fig. 1). Un événement est représenté par un ensemble de coordonnées x , y , z et t . L'espace-temps est donc quadridimensionnel . Les événements mathématiques ont une durée nulle et représentent un point unique dans l'espace-temps.
Le parcours d'une particule dans l'espace-temps peut être considéré comme une succession d'événements. La série d'événements peut être liée pour former une ligne qui représente la progression d'une particule dans l'espace-temps. Cette ligne s'appelle la ligne d'univers de la particule .
Mathématiquement, l'espace-temps est une variété , c'est-à-dire qu'il apparaît localement "plat" près de chaque point de la même manière qu'à des échelles suffisamment petites, un globe apparaît plat. Un facteur d'échelle, (conventionnellement appelé la vitesse de la lumière ) relie les distances mesurées dans l'espace aux distances mesurées dans le temps. L'ampleur de ce facteur d'échelle (près de 300 000 kilomètres ou 190 000 miles dans l'espace équivaut à une seconde dans le temps), ainsi que le fait que l'espace-temps est une variété, implique qu'à des vitesses ordinaires, non relativistes et à une échelle humaine ordinaire distances, il y a peu de choses que les humains pourraient observer qui soient sensiblement différentes de ce qu'ils pourraient observer si le monde était euclidien. Ce n'est qu'avec l'avènement de mesures scientifiques sensibles au milieu des années 1800, telles que l' expérience Fizeau et l' expérience Michelson-Morley , que des écarts déroutants ont commencé à être notés entre l'observation et les prédictions basées sur l'hypothèse implicite de l'espace euclidien.

Dans la relativité restreinte, un observateur désignera, dans la plupart des cas, un cadre de référence à partir duquel un ensemble d'objets ou d'événements est mesuré. Cet usage diffère considérablement du sens anglais ordinaire du terme. Les cadres de référence sont par nature des constructions non locales, et selon cet usage du terme, cela n'a pas de sens de parler d'un observateur comme ayant un emplacement. Sur la figure 1-1, imaginons que le référentiel considéré soit équipé d'un réseau dense d'horloges, synchronisées dans ce référentiel, qui s'étend indéfiniment dans les trois dimensions de l'espace. Tout emplacement spécifique dans le réseau n'est pas important. Le réseau d'horloges est utilisé pour déterminer l'heure et la position des événements qui se déroulent dans l'ensemble du cadre. Le terme observateur désigne l'ensemble des horloges associées à un référentiel inertiel. Dans ce cas idéalisé, chaque point de l'espace est associé à une horloge, et ainsi les horloges enregistrent chaque événement instantanément, sans délai entre un événement et son enregistrement. Un vrai observateur verra cependant un délai entre l'émission d'un signal et sa détection dû à la vitesse de la lumière. Pour synchroniser les horloges, dans la réduction des données suite à une expérience, l'heure à laquelle un signal est reçu sera corrigée pour refléter son heure réelle si elle avait été enregistrée par un réseau idéalisé d'horloges.
Dans de nombreux livres sur la relativité restreinte, en particulier les plus anciens, le mot "observateur" est utilisé dans le sens le plus ordinaire du mot. Il ressort généralement du contexte quel sens a été adopté.
Les physiciens font la distinction entre ce que l'on mesure ou observe (après avoir pris en compte les retards de propagation du signal) et ce que l'on voit visuellement sans ces corrections. Le fait de ne pas comprendre la différence entre ce que l'on mesure/observe et ce que l'on voit est la source de beaucoup d'erreurs chez les étudiants débutants en relativité.
Histoire
Au milieu des années 1800, diverses expériences telles que l'observation de la tache d'Arago et les mesures différentielles de la vitesse de la lumière dans l'air par rapport à l'eau ont été considérées comme ayant prouvé la nature ondulatoire de la lumière par opposition à une théorie corpusculaire . La propagation des ondes était alors supposée nécessiter l'existence d'un milieu ondulatoire ; dans le cas des ondes lumineuses, cela a été considéré comme un hypothétique éther luminifère . Cependant, les différentes tentatives pour établir les propriétés de ce milieu hypothétique ont donné des résultats contradictoires. Par exemple, l' expérience Fizeau de 1851, menée par le physicien français Hippolyte Fizeau , a démontré que la vitesse de la lumière dans l'eau courante était inférieure à la somme de la vitesse de la lumière dans l'air et de la vitesse de l'eau d'une quantité dépendant de la vitesse de l'eau. index de réfraction. Entre autres problèmes, la dépendance de l'entraînement partiel de l' éther impliqué par cette expérience sur l'indice de réfraction (qui dépend de la longueur d'onde) a conduit à la conclusion désagréable que l'éther s'écoule simultanément à différentes vitesses pour différentes couleurs de lumière. La célèbre expérience Michelson-Morley de 1887 (Fig. 1-2) n'a montré aucune influence différentielle des mouvements de la Terre à travers l'éther hypothétique sur la vitesse de la lumière, et l'explication la plus probable, le déplacement complet de l'éther, était en conflit avec l'observation de l'éther stellaire . aberration .
George Francis FitzGerald en 1889, et Hendrik Lorentz en 1892, ont indépendamment proposé que les corps matériels voyageant à travers l'éther fixe étaient physiquement affectés par leur passage, se contractant dans la direction du mouvement d'une quantité qui était exactement ce qui était nécessaire pour expliquer les résultats négatifs de l'expérience de Michelson-Morley. (Aucun changement de longueur ne se produit dans les directions transversales à la direction du mouvement.)
En 1904, Lorentz avait élargi sa théorie de telle sorte qu'il était arrivé à des équations formellement identiques à celles qu'Einstein devait dériver plus tard (c'est-à-dire la transformation de Lorentz ), mais avec une interprétation fondamentalement différente. En tant que théorie de la dynamique (l'étude des forces et des couples et de leur effet sur le mouvement), sa théorie supposait des déformations physiques réelles des constituants physiques de la matière. Les équations de Lorentz prédisaient une quantité qu'il appelait le temps local , avec laquelle il pouvait expliquer l' aberration de la lumière , l'expérience de Fizeau et d'autres phénomènes. Cependant, Lorentz considérait le temps local comme un outil mathématique auxiliaire, une astuce en quelque sorte, pour simplifier la transformation d'un système à un autre.
D'autres physiciens et mathématiciens du tournant du siècle ont failli arriver à ce que l'on appelle actuellement l'espace-temps. Einstein lui-même a noté qu'avec tant de personnes démêlant des pièces séparées du puzzle, "la théorie restreinte de la relativité, si nous considérons son développement rétrospectivement, était mûre pour être découverte en 1905".
Un exemple important est Henri Poincaré , qui en 1898 a soutenu que la simultanéité de deux événements est une question de convention. En 1900, il a reconnu que «l'heure locale» de Lorentz est en fait ce qui est indiqué par des horloges en mouvement en appliquant une définition explicitement opérationnelle de la synchronisation d'horloge en supposant une vitesse de lumière constante. En 1900 et 1904, il suggéra l'indétectabilité inhérente de l'éther en insistant sur la validité de ce qu'il appelait le principe de relativité , et en 1905/1906 il perfectionna mathématiquement la théorie des électrons de Lorentz afin de la mettre en conformité avec le postulat de la relativité. . Tout en discutant de diverses hypothèses sur la gravitation invariante de Lorentz, il a introduit le concept innovant d'un espace-temps à 4 dimensions en définissant divers quatre vecteurs , à savoir quatre positions , quatre vitesses et quatre forces . Il n'a cependant pas poursuivi le formalisme en 4 dimensions dans des articles ultérieurs, déclarant que cette ligne de recherche semblait "entraîner une grande douleur pour un profit limité", concluant finalement "que le langage en trois dimensions semble le mieux adapté à la description de notre monde". ". De plus, même en 1909, Poincaré continuait de croire en l'interprétation dynamique de la transformée de Lorentz. Pour ces raisons et d'autres, la plupart des historiens des sciences soutiennent que Poincaré n'a pas inventé ce qu'on appelle maintenant la relativité restreinte.
En 1905, Einstein a introduit la relativité restreinte (même sans utiliser les techniques du formalisme de l'espace-temps) dans sa compréhension moderne en tant que théorie de l'espace et du temps. Alors que ses résultats sont mathématiquement équivalents à ceux de Lorentz et Poincaré, Einstein a montré que les transformations de Lorentz ne sont pas le résultat d'interactions entre la matière et l'éther, mais concernent plutôt la nature de l'espace et du temps lui-même. Il a obtenu tous ses résultats en reconnaissant que toute la théorie peut être construite sur deux postulats : le principe de relativité et le principe de constance de la vitesse de la lumière.
Einstein a effectué son analyse en termes de cinématique (l'étude des corps en mouvement sans référence aux forces) plutôt qu'en termes de dynamique. Son travail introduisant le sujet était rempli d'images vives impliquant l'échange de signaux lumineux entre des horloges en mouvement, des mesures minutieuses des longueurs de tiges mobiles et d'autres exemples similaires.
De plus, Einstein en 1905 a remplacé les tentatives précédentes d'une relation masse-énergie électromagnétique en introduisant l' équivalence générale de la masse et de l'énergie , qui a contribué à sa formulation ultérieure du principe d'équivalence en 1907, qui déclare l'équivalence de la masse inertielle et gravitationnelle. En utilisant l'équivalence masse-énergie, Einstein a montré, en outre, que la masse gravitationnelle d'un corps est proportionnelle à son contenu énergétique, ce qui a été l'un des premiers résultats du développement de la relativité générale . Bien qu'il semblerait qu'il n'ait pas d'abord pensé géométriquement à l'espace-temps, dans le développement ultérieur de la relativité générale, Einstein a pleinement incorporé le formalisme de l'espace-temps.
Quand Einstein publie en 1905, un autre de ses concurrents, son ancien professeur de mathématiques Hermann Minkowski , est également parvenu à la plupart des éléments de base de la relativité restreinte. Max Born a raconté une rencontre qu'il avait faite avec Minkowski, cherchant à être l'étudiant/collaborateur de Minkowski :
Je suis allé à Cologne, j'ai rencontré Minkowski et j'ai entendu sa célèbre conférence "Espace et Temps" prononcée le 2 septembre 1908. [...] Il m'a dit plus tard qu'il avait été très choqué lorsqu'Einstein a publié son article dans lequel l'équivalence des différents temps locaux des observateurs se déplaçant les uns par rapport aux autres a été prononcée ; car il était parvenu aux mêmes conclusions de manière indépendante mais ne les a pas publiées parce qu'il souhaitait d'abord élaborer la structure mathématique dans toute sa splendeur. Il n'a jamais revendiqué de priorité et a toujours donné à Einstein sa pleine part dans la grande découverte.
Minkowski s'était préoccupé de l'état de l'électrodynamique après les expériences perturbatrices de Michelson au moins depuis l'été 1905, lorsque Minkowski et David Hilbert ont dirigé un séminaire avancé auquel ont participé des physiciens notables de l'époque pour étudier les articles de Lorentz, Poincaré et al. Cependant, on ne sait pas du tout quand Minkowski a commencé à formuler la formulation géométrique de la relativité restreinte qui devait porter son nom, ou dans quelle mesure il a été influencé par l'interprétation quadridimensionnelle de Poincaré de la transformation de Lorentz. Il n'est pas non plus clair s'il a jamais pleinement apprécié la contribution critique d'Einstein à la compréhension des transformations de Lorentz, pensant que le travail d'Einstein était une extension du travail de Lorentz.
Le 5 novembre 1907 (un peu plus d'un an avant sa mort), Minkowski a présenté son interprétation géométrique de l'espace-temps dans une conférence à la société mathématique de Göttingen sous le titre, Le principe de relativité ( Das Relativitätsprinzip ). Le 21 septembre 1908, Minkowski présenta son célèbre discours, L'espace et le temps ( Raum und Zeit ), à la Société allemande des scientifiques et des médecins. Les premiers mots de Space and Time incluent la célèbre déclaration de Minkowski selon laquelle "Désormais, l'espace pour lui-même et le temps pour lui-même se réduiront complètement à une simple ombre, et seule une sorte d'union des deux préservera l'indépendance". Space and Time comprenait la première présentation publique de diagrammes d'espace-temps (Fig. 1-4), et comprenait une démonstration remarquable que le concept de l' intervalle invariant ( discuté ci-dessous ), ainsi que l'observation empirique que la vitesse de la lumière est finie, permettent dérivation de l'intégralité de la relativité restreinte.
Le concept d'espace-temps et le groupe de Lorentz sont étroitement liés à certains types de géométries sphériques , hyperboliques ou conformes et à leurs groupes de transformation déjà développés au XIXe siècle, dans lesquels des intervalles invariants analogues à l'intervalle d'espace-temps sont utilisés.
Einstein, pour sa part, a d'abord rejeté l'interprétation géométrique de la relativité restreinte de Minkowski, la considérant comme überflüssige Gelehrsamkeit (savoir superflu). Cependant, pour compléter sa recherche de la relativité générale commencée en 1907, l'interprétation géométrique de la relativité s'avère vitale et, en 1916, Einstein reconnaît pleinement sa dette envers Minkowski, dont l'interprétation facilite grandement le passage à la relativité générale. Puisqu'il existe d'autres types d'espace-temps, tels que l'espace-temps courbe de la relativité générale, l'espace-temps de la relativité restreinte est aujourd'hui connu sous le nom d' espace-temps de Minkowski.
L'espace-temps en relativité restreinte
Intervalle d'espace-temps
En trois dimensions, la distance entre deux points peut être définie à l'aide du théorème de Pythagore :
Bien que deux observateurs puissent mesurer la position x , y et z des deux points en utilisant des systèmes de coordonnées différents, la distance entre les points sera la même pour les deux (en supposant qu'ils mesurent en utilisant les mêmes unités). La distance est "invariante".
En relativité restreinte, cependant, la distance entre deux points n'est plus la même si elle est mesurée par deux observateurs différents lorsque l'un des observateurs se déplace, à cause de la contraction de Lorentz . La situation est encore plus compliquée si les deux points sont séparés aussi bien dans le temps que dans l'espace. Par exemple, si un observateur voit deux événements se produire au même endroit, mais à des moments différents, une personne se déplaçant par rapport au premier observateur verra les deux événements se produire à des endroits différents, car (de son point de vue) ils sont stationnaires , et la position de l'événement s'éloigne ou s'approche. Ainsi, une mesure différente doit être utilisée pour mesurer la "distance" effective entre deux événements.
Dans l'espace-temps à quatre dimensions, l'analogue de la distance est l'intervalle. Bien que le temps soit une quatrième dimension, il est traité différemment des dimensions spatiales. L'espace de Minkowski diffère donc à bien des égards de l'espace euclidien à quatre dimensions . La raison fondamentale de la fusion de l'espace et du temps dans l'espace-temps est que l'espace et le temps ne sont pas invariants séparément, c'est-à-dire que, dans les conditions appropriées, différents observateurs seront en désaccord sur la durée entre deux événements (à cause de la dilatation du temps ) ou la distance entre les deux événements (à cause de la contraction de la longueur ). Mais la relativité restreinte fournit un nouvel invariant, appelé l' intervalle spatio -temporel , qui combine les distances dans l'espace et dans le temps. Tous les observateurs qui mesurent le temps et la distance entre deux événements quelconques finiront par calculer le même intervalle d'espace-temps. Supposons qu'un observateur mesure deux événements comme étant séparés dans le temps par et par une distance spatiale Alors l'intervalle spatio-temporel entre les deux événements qui sont séparés par une distance dans l'espace et par dans la coordonnée est :
ou pour trois dimensions d'espace,
La vitesse constante de la lumière convertit les unités de temps (comme les secondes) en unités d'espace (comme les mètres). L'intervalle au carré est une mesure de la séparation entre les événements A et B qui sont séparés dans le temps et en plus dans l'espace, soit parce qu'il y a deux objets distincts subissant des événements, soit parce qu'un seul objet dans l'espace se déplace par inertie entre ses événements. L'intervalle de séparation est obtenu en mettant au carré la distance spatiale séparant l'événement B de l'événement A et en la soustrayant du carré de la distance spatiale parcourue par un signal lumineux dans ce même intervalle de temps . Si la séparation des événements est due à un signal lumineux, alors cette différence s'annule et .
Lorsque l'événement considéré est infiniment proche l'un de l'autre, alors on peut écrire
Dans un référentiel inertiel différent, disons avec des coordonnées , l'intervalle d'espace-temps peut être écrit sous la même forme que ci-dessus. En raison de la constance de la vitesse de la lumière, les événements lumineux dans tous les référentiels inertiels appartiennent à l'intervalle zéro, . Pour tout autre événement infinitésimal où , on peut prouver ce qui à son tour lors de l'intégration conduit à . L'invariance de l'intervalle de tout événement entre tous les référentiels intertiels est l'un des résultats fondamentaux de la théorie de la relativité restreinte.
Bien que par souci de brièveté, on voit fréquemment des expressions d'intervalle exprimées sans deltas, y compris dans la plupart des discussions qui suivent, il faut comprendre qu'en général, signifie , etc. Nous sommes toujours concernés par les différences de valeurs de coordonnées spatiales ou temporelles appartenant à deux événements, et puisqu'il n'y a pas d'origine préférée, les valeurs de coordonnées uniques n'ont pas de signification essentielle.
L'équation ci-dessus est similaire au théorème de Pythagore, sauf avec un signe moins entre les termes et . L'intervalle d'espace-temps est la quantité et non elle-même. La raison en est que, contrairement aux distances dans la géométrie euclidienne, les intervalles dans l'espace-temps de Minkowski peuvent être négatifs. Plutôt que de traiter des racines carrées de nombres négatifs, les physiciens considèrent habituellement comme un symbole distinct en soi, plutôt que le carré de quelque chose.
En général, peut prendre n'importe quelle valeur du nombre réel. Si est positif, l'intervalle spatio-temporel est appelé timelike . Étant donné que la distance spatiale parcourue par tout objet massif est toujours inférieure à la distance parcourue par la lumière pendant le même intervalle de temps, les intervalles réels sont toujours de type temporel. Si est négatif, l'intervalle spatio-temporel est dit spacelike , où l'intervalle spatio-temporel est imaginaire. Les intervalles d'espace-temps sont égaux à zéro lorsque En d'autres termes, l'intervalle d'espace-temps entre deux événements sur la ligne d'univers de quelque chose se déplaçant à la vitesse de la lumière est égal à zéro. Un tel intervalle est appelé lightlike ou null . Un photon arrivant dans notre œil depuis une étoile lointaine n'aura pas vieilli, bien qu'il ait (de notre point de vue) passé des années sur son passage.
Un diagramme d'espace-temps est généralement dessiné avec un seul espace et une seule coordonnée de temps. La figure 2-1 présente un diagramme de l'espace-temps illustrant les lignes d'univers (c'est-à-dire les trajets dans l'espace-temps) de deux photons, A et B, provenant du même événement et allant dans des directions opposées. De plus, C illustre la ligne d'univers d'un objet plus lent que la vitesse de la lumière. La coordonnée temporelle verticale est mise à l'échelle de sorte qu'elle ait les mêmes unités (mètres) que la coordonnée spatiale horizontale. Puisque les photons voyagent à la vitesse de la lumière, leurs lignes d'univers ont une pente de ±1. En d'autres termes, chaque mètre parcouru par un photon vers la gauche ou vers la droite nécessite environ 3,3 nanosecondes de temps.
Deux conventions de signes sont utilisées dans la littérature sur la relativité :
et
Ces conventions de signes sont associées aux signatures métriques (+−−−) et (−+++). Une variation mineure consiste à placer la coordonnée de temps en dernier plutôt qu'en premier. Les deux conventions sont largement utilisées dans le domaine d'études.
Cadres de référence
Pour mieux comprendre comment les coordonnées spatio-temporelles mesurées par les observateurs dans différents cadres de référence se comparent les unes aux autres, il est utile de travailler avec une configuration simplifiée avec des cadres dans une configuration standard. Avec précaution, cela permet de simplifier les calculs sans perte de généralité dans les conclusions auxquelles on parvient. Sur la Fig. 2-2, deux référentiels galiléens (c'est-à-dire des référentiels conventionnels à 3 espaces) sont affichés en mouvement relatif. La trame S appartient à un premier observateur O, et la trame S' (prononcez "S prime") appartient à un deuxième observateur O'.
- Les axes x , y , z du cadre S sont orientés parallèlement aux axes amorcés respectifs du cadre S'.
- Le cadre S′ se déplace dans la direction x du cadre S avec une vitesse constante v telle que mesurée dans le cadre S.
- Les origines des trames S et S' sont confondues lorsque le temps t = 0 pour la trame S et t ' = 0 pour la trame S'.
La Fig. 2-3a redessine la Fig. 2-2 dans une orientation différente. La figure 2-3b illustre un diagramme d'espace-temps du point de vue de l'observateur O. Puisque S et S′ sont en configuration standard, leurs origines coïncident aux instants t = 0 dans la trame S et t ′ = 0 dans la trame S′. L' axe ct ′ passe par les événements du cadre S ′ qui ont x ′ = 0. Mais les points avec x ′ = 0 se déplacent dans la direction x du cadre S avec une vitesse v , de sorte qu'ils ne coïncident pas avec le ct l'axe à tout moment autre que zéro. Par conséquent, l' axe ct ′ est incliné par rapport à l' axe ct d'un angle θ donné par
L' axe x ' est également incliné par rapport à l' axe x . Pour déterminer l'angle de cette inclinaison, on rappelle que la pente de la ligne d'univers d'une impulsion lumineuse est toujours ±1. La figure 2-3c présente un diagramme espace-temps du point de vue de l'observateur O'. L'événement P représente l'émission d'une impulsion lumineuse à x ′ = 0, ct ′ = − a . L'impulsion est réfléchie par un miroir situé à une distance a de la source lumineuse (événement Q), et revient vers la source lumineuse à x ' = 0, ct ' = a (événement R).
Les mêmes événements P, Q, R sont tracés sur la Fig. 2-3b dans le cadre de l'observateur O. Les trajets lumineux ont des pentes = 1 et −1, de sorte que △PQR forme un triangle rectangle avec PQ et QR tous deux à 45 degrés aux axes x et ct . Puisque OP = OQ = OR, l'angle entre x ′ et x doit également être θ .
Alors que le cadre de repos a des axes d'espace et de temps qui se rejoignent à angle droit, le cadre mobile est dessiné avec des axes qui se rejoignent à angle aigu. Les cadres sont en fait équivalents. L'asymétrie est due à des distorsions inévitables dans la manière dont les coordonnées de l'espace-temps peuvent être mappées sur un plan cartésien , et ne doit pas être considérée comme plus étrange que la manière dont, sur une projection de Mercator de la Terre, les tailles relatives des masses terrestres proches des pôles (Groenland et l'Antarctique) sont très exagérées par rapport aux masses terrestres proches de l'équateur.
Cône de lumière
Dans la Fig. 2–4, l'événement O est à l'origine d'un diagramme d'espace-temps et les deux lignes diagonales représentent tous les événements qui ont un intervalle d'espace-temps nul par rapport à l'événement d'origine. Ces deux lignes forment ce qu'on appelle le cône de lumière de l'événement O, puisque l'ajout d'une deuxième dimension spatiale (Fig. 2-5) fait apparaître celle de deux cônes circulaires droits se rejoignant par leurs sommets en O. Un cône se prolonge dans le futur (t>0), l'autre dans le passé (t<0).
Un cône de lumière (double) divise l'espace-temps en régions séparées par rapport à son sommet. L'intérieur du futur cône de lumière se compose de tous les événements qui sont séparés du sommet par plus de temps (distance temporelle) que nécessaire pour franchir leur distance spatiale à la vitesse de la lumière ; ces événements comprennent le futur temporel de l'événement O. De même, le passé temporel comprend les événements intérieurs du cône de lumière passé. Ainsi, dans des intervalles temporels, Δ ct est supérieur à Δ x , ce qui rend les intervalles temporels positifs. La région extérieure au cône de lumière est constituée d'événements qui sont séparés de l'événement O par plus d' espace qu'il ne peut être traversé à la vitesse de la lumière dans le temps donné . Ces événements comprennent la région dite spatiale de l'événement O, notée "Ailleurs" sur la figure 2-4. Les événements sur le cône de lumière lui-même sont dits légers (ou séparés par zéro ) de O. En raison de l'invariance de l'intervalle d'espace-temps, tous les observateurs attribueront le même cône de lumière à un événement donné, et seront donc d'accord sur cette division de l'espace-temps. .
Le cône de lumière a un rôle essentiel dans le concept de causalité . Il est possible qu'un signal non plus rapide que la vitesse de la lumière se déplace de la position et de l'heure de O à la position et à l'heure de D (Fig. 2-4). Il est donc possible que l'événement O ait une influence causale sur l'événement D. Le futur cône de lumière contient tous les événements qui pourraient être causalement influencés par O. De même, il est possible qu'un signal non plus rapide que la vitesse de la lumière voyager de la position et de l'heure de A, à la position et à l'heure de O. Le cône de lumière passé contient tous les événements qui pourraient avoir une influence causale sur O. En revanche, en supposant que les signaux ne peuvent pas voyager plus vite que la vitesse de la lumière, tout un événement, comme par exemple B ou C, dans la région semblable à l'espace (Ailleurs), ne peut ni affecter l'événement O, ni être affecté par l'événement O employant une telle signalisation. Sous cette hypothèse, toute relation causale entre l'événement O et tout événement dans la région spatiale d'un cône de lumière est exclue.
Relativité de la simultanéité
Tous les observateurs conviendront que pour un événement donné, un événement dans le futur cône de lumière de l'événement donné se produit après l'événement donné. De même, pour tout événement donné, un événement dans le cône de lumière passé de l'événement donné se produit avant l'événement donné. La relation avant-après observée pour des événements séparés dans le temps reste inchangée quel que soit le cadre de référence de l'observateur, c'est-à-dire quel que soit le mouvement de l'observateur. La situation est tout à fait différente pour les événements séparés par un espace. La figure 2-4 a été tirée du cadre de référence d'un observateur se déplaçant à v = 0. À partir de ce cadre de référence, on observe que l'événement C se produit après l'événement O et que l'événement B se produit avant l'événement O. À partir d'une référence différente cadre, les ordres de ces événements non liés causalement peuvent être inversés. En particulier, on note que si deux événements sont simultanés dans un cadre de référence particulier, ils sont nécessairement séparés par un intervalle de type espace et sont donc liés de manière non causale. L'observation que la simultanéité n'est pas absolue, mais dépend du cadre de référence de l'observateur, est appelée la relativité de la simultanéité .
La figure 2-6 illustre l'utilisation des diagrammes d'espace-temps dans l'analyse de la relativité de la simultanéité. Les événements dans l'espace-temps sont invariants, mais les cadres de coordonnées se transforment comme indiqué ci-dessus pour la figure 2-3. Les trois événements (A, B, C) sont simultanés à partir du référentiel d'un observateur se déplaçant à v = 0. À partir du référentiel d'un observateur se déplaçant à v = 0,3 c , les événements semblent se produire dans l'ordre C, B , A. A partir du référentiel d'un observateur se déplaçant à v = −0.5 c , les événements semblent se produire dans l'ordre A, B, C . La ligne blanche représente un plan de simultanéité déplacé du passé de l'observateur vers le futur de l'observateur, mettant en évidence les événements qui y résident. La zone grise est le cône de lumière de l'observateur, qui reste invariant.
Un intervalle d'espace-temps de type spatial donne la même distance qu'un observateur mesurerait si les événements mesurés étaient simultanés pour l'observateur. Un intervalle d'espace-temps de type spatial fournit donc une mesure de la distance appropriée , c'est-à-dire la vraie distance = De même, un intervalle d'espace-temps de type temporel donne la même mesure de temps que celle qui serait présentée par le tic-tac cumulatif d'une horloge qui se déplace le long d'une ligne mondiale donnée. Un intervalle d'espace-temps de type temps fournit donc une mesure du temps propre =
Hyperbole invariante
Dans l'espace euclidien (ayant uniquement des dimensions spatiales), l'ensemble des points équidistants (en utilisant la métrique euclidienne) d'un point forme un cercle (en deux dimensions) ou une sphère (en trois dimensions). Dans l'espace-temps de Minkowski à (1 + 1) dimension (ayant une dimension temporelle et une dimension spatiale), les points à un intervalle d'espace-temps constant loin de l'origine (en utilisant la métrique de Minkowski) forment des courbes données par les deux équations
avec une constante réelle positive. Ces équations décrivent deux familles d'hyperboles dans un diagramme d'espace-temps x - ct , appelées hyperboles invariantes .
Dans la Fig. 2-7a, chaque hyperbole magenta relie tous les événements ayant une certaine séparation spatiale fixe de l'origine, tandis que les hyperboles vertes relient les événements de séparation temporelle égale.
Les hyperboles magenta, qui traversent l' axe des x , sont des courbes temporelles, c'est-à-dire que ces hyperboles représentent des chemins réels qui peuvent être parcourus par des particules (en accélération constante) dans l'espace-temps : entre deux événements quelconques sur une hyperbole, une relation de causalité est possible, car l'inverse de la pente - représentant la vitesse nécessaire - pour toute sécante est inférieur à . D'autre part, les hyperboles vertes, qui traversent l' axe ct , sont des courbes spatiales car tous les intervalles le long de ces hyperboles sont des intervalles spatiaux : aucune causalité n'est possible entre deux points quelconques sur l'une de ces hyperboles, car toutes les sécantes représentent des vitesses supérieures à .
La figure 2-7b reflète la situation dans l'espace-temps de Minkowski à (1+2) dimensions (une dimension temporelle et deux dimensions spatiales) avec les hyperboloïdes correspondants. Les hyperboles invariantes déplacées par des intervalles spatiaux à partir de l'origine génèrent des hyperboloïdes d'une nappe, tandis que les hyperboles invariantes déplacées par des intervalles temporels à partir de l'origine génèrent des hyperboloïdes à deux nappes.
La frontière (1 + 2) dimensionnelle entre les hyperboloïdes de type espace et temps, établie par les événements formant un intervalle espace-temps nul à l'origine, est constituée par la dégénérescence des hyperboloïdes vers le cône de lumière. Dans les dimensions (1+1), les hyperboles dégénèrent en deux lignes grises à 45° représentées sur la Fig. 2-7a.
Dilatation du temps et contraction de la longueur
La Fig. 2-8 illustre l'hyperbole invariante pour tous les événements pouvant être atteints depuis l'origine dans un temps propre de 5 mètres (environ1,67 × 10 −8 s ). Différentes lignes de monde représentent des horloges se déplaçant à des vitesses différentes. Une horloge qui est stationnaire par rapport à l'observateur a une ligne d'univers qui est verticale, et le temps écoulé mesuré par l'observateur est le même que le temps propre. Pour une horloge se déplaçant à 0,3 c , le temps écoulé mesuré par l'observateur est de 5,24 mètres (1,75 × 10 −8 s ), tandis que pour une horloge se déplaçant à 0,7 c , le temps écoulé mesuré par l'observateur est de 7,00 mètres (2,34 × 10 -8 s ). Ceci illustre le phénomène connu sous le nom de dilatation du temps . Les horloges qui voyagent plus rapidement prennent plus de temps (dans le cadre de l'observateur) pour marquer la même quantité de temps propre, et elles voyagent plus loin le long de l'axe des x dans ce temps propre qu'elles ne l'auraient fait sans dilatation du temps. La mesure de la dilatation temporelle par deux observateurs dans des référentiels inertiels différents est mutuelle. Si l'observateur O mesure les horloges de l'observateur O' comme fonctionnant plus lentement dans son cadre, l'observateur O' mesurera à son tour les horloges de l'observateur O comme fonctionnant plus lentement.
La contraction de la longueur , comme la dilatation du temps, est une manifestation de la relativité de la simultanéité. La mesure de la longueur nécessite la mesure de l'intervalle spatio-temporel entre deux événements simultanés dans son référentiel. Mais les événements qui sont simultanés dans un référentiel ne sont, en général, pas simultanés dans d'autres référentiels.
La figure 2-9 illustre les mouvements d'une tige de 1 m qui se déplace à 0,5 c le long de l' axe x . Les bords de la bande bleue représentent les lignes d'univers des deux extrémités de la tige. L'hyperbole invariante illustre des événements séparés de l'origine par un intervalle spatial de 1 m. Les points terminaux O et B mesurés lorsque t ' = 0 sont des événements simultanés dans la trame S'. Mais pour un observateur dans le cadre S, les événements O et B ne sont pas simultanés. Pour mesurer la longueur, l'observateur dans le cadre S mesure les extrémités de la tige projetées sur l' axe des x le long de leurs lignes d'univers. La projection de la feuille du monde de la tige sur l' axe des x donne la longueur raccourcie OC.
(non illustré) Tracer une ligne verticale passant par A de sorte qu'elle coupe l' axe x 'démontre que, même si OB est raccourci du point de vue de l'observateur O, OA est également raccourci du point de vue de l'observateur O '. De la même manière que chaque observateur mesure les horloges de l'autre comme étant lentes, chaque observateur mesure les dirigeants de l'autre comme étant contractés.
En ce qui concerne la contraction mutuelle des longueurs, la figure 2-9 montre que les cadres amorcés et non amorcés sont mutuellement tournés d'un angle hyperbolique (analogue aux angles ordinaires en géométrie euclidienne). Du fait de cette rotation, la projection d'un bâtonnet de mètre amorcé sur l'axe x non amorcé est raccourcie, tandis que la projection d'un bâtonnet de mètre non amorcé sur l'axe x' amorcé est également raccourcie.
Dilatation mutuelle du temps et paradoxe des jumeaux
Dilatation mutuelle du temps
La dilatation mutuelle du temps et la contraction de la longueur ont tendance à frapper les débutants comme des concepts intrinsèquement contradictoires. Si un observateur dans l'image S mesure une horloge, au repos dans l'image S', comme fonctionnant plus lentement que la sienne', alors que S' se déplace à la vitesse v dans S, alors le principe de relativité exige qu'un observateur dans l'image S' mesure également une horloge dans le cadre S, se déplaçant à la vitesse − v dans S', comme fonctionnant plus lentement que la sienne. Comment deux horloges peuvent fonctionner toutes les deux plus lentement que l'autre est une question importante qui "va au cœur de la compréhension de la relativité restreinte".
Cette apparente contradiction provient d'une mauvaise prise en compte des différents réglages des mesures nécessaires et connexes. Ces paramètres permettent une explication cohérente de la seule contradiction apparente . Il ne s'agit pas du tic-tac abstrait de deux horloges identiques, mais de la façon de mesurer dans une image la distance temporelle de deux tic-tac d'une horloge en mouvement. Il s'avère qu'en observant mutuellement la durée entre les ticks d'horloges, chacune se déplaçant dans le cadre respectif, différents ensembles d'horloges doivent être impliqués. Pour mesurer dans la trame S la durée de tic d'une horloge mobile W′ (au repos dans S′), on utilise deux horloges supplémentaires synchronisées W 1 et W 2 au repos en deux points arbitrairement fixes dans S avec la distance spatiale d .
- Deux événements peuvent être définis par la condition "deux horloges sont simultanément à un même endroit", c'est-à-dire lorsque W' passe chacun W 1 et W 2 . Pour les deux événements, les deux lectures des horloges colocalisées sont enregistrées. La différence des deux lectures de W 1 et W 2 est la distance temporelle des deux événements dans S, et leur distance spatiale est d . La différence des deux lectures de W′ est la distance temporelle des deux événements dans S′. Dans S′ ces événements sont seulement séparés dans le temps, ils se produisent au même endroit dans S′. En raison de l'invariance de l'intervalle d'espace-temps parcouru par ces deux événements, et de la séparation spatiale d non nulle dans S, la distance temporelle dans S' doit être inférieure à celle dans S : la plus petite distance temporelle entre les deux événements, résultant de la lectures de l'horloge mobile W′, appartient à l' horloge W′ la plus lente .
A l'inverse, pour juger dans la trame S' de la distance temporelle de deux événements sur une horloge mobile W (au repos dans S), il faut deux horloges au repos dans S'.
- Dans cette comparaison, l'horloge W se déplace avec une vitesse − v . L'enregistrement à nouveau des quatre lectures pour les événements, définis par "deux horloges simultanément à un endroit", se traduit par les distances temporelles analogues des deux événements, désormais séparés temporellement et spatialement en S ', et seulement séparés temporellement mais colocalisés en S . garder l'intervalle spatio-temporel invariant, la distance temporelle dans S doit être plus petite que dans S′, à cause de la séparation spatiale des événements dans S′ : maintenant on observe que l'horloge W tourne plus lentement.
Les enregistrements nécessaires pour les deux jugements, avec "une horloge mobile" et "deux horloges au repos" respectivement en S ou S', impliquent deux ensembles différents, chacun avec trois horloges. Puisqu'il existe différents ensembles d'horloges impliquées dans les mesures, il n'y a aucune nécessité inhérente que les mesures soient réciproquement "cohérentes" de sorte que, si un observateur mesure que l'horloge en mouvement est lente, l'autre observateur mesure que l'horloge de l'un est rapide.
La figure 2-10 illustre la discussion précédente de la dilatation mutuelle du temps avec les diagrammes de Minkowski. L'image du haut reflète les mesures vues du cadre S "au repos" avec des axes rectangulaires non amorcés, et du cadre S '"se déplaçant avec v > 0", coordonné par des axes amorcés, obliques, inclinés vers la droite; l'image du bas montre le cadre S '"au repos" avec des coordonnées rectangulaires amorcées, et le cadre S "se déplaçant avec - v <0", avec des axes obliques non amorcés, inclinés vers la gauche.
Chaque ligne tracée parallèlement à un axe spatial ( x , x ') représente une ligne de simultanéité. Tous les événements sur une telle ligne ont la même valeur temporelle ( ct , ct ′). De même, chaque ligne tracée parallèlement à un axe temporel ( ct , ct' ) représente une ligne de valeurs de coordonnées spatiales égales ( x , x ').
- On peut désigner dans les deux images l'origine O (= O ′ ) comme l'événement, où "l'horloge en mouvement" respective est colocalisée avec la "première horloge au repos" dans les deux comparaisons. De toute évidence, pour cet événement, les lectures sur les deux horloges dans les deux comparaisons sont nulles. En conséquence, les lignes d'univers des horloges en mouvement sont les axes inclinés vers la droite ct ′ (images du haut, horloge W′) et les axes inclinés vers la gauche ct (images du bas, horloge W). Les lignes d'univers de W 1 et W′ 1 sont les axes de temps verticaux correspondants ( ct dans les images du haut et ct ′ dans les images du bas).
- Dans l'image du haut, la place de W 2 est considérée comme étant A x > 0, et donc la ligne d'univers (non représentée sur les images) de cette horloge coupe la ligne d'univers de l'horloge mobile (l' axe ct ′) dans l'événement étiqueté A , où "deux horloges sont simultanément au même endroit". Dans l'image du bas, la place pour W′ 2 est considérée comme étant C x ′ < 0, et donc dans cette mesure l'horloge mobile W dépasse W′ 2 dans l'événement C .
- Dans l'image du haut, la coordonnée ct A t de l'événement A (la lecture de W 2 ) est étiquetée B , donnant ainsi le temps écoulé entre les deux événements, mesuré avec W 1 et W 2 , comme OB . Pour une comparaison, la longueur de l'intervalle de temps OA , mesuré avec W', doit être transformée à l'échelle de l' axe ct- . Ceci est fait par l'hyperbole invariante (voir aussi Fig. 2-8) passant par A , reliant tous les événements avec le même intervalle d'espace-temps à partir de l'origine que A . Cela donne l'événement C sur l' axe ct , et évidemment : OC < OB , l'horloge "mobile" W′ tourne plus lentement.
Pour montrer la dilatation mutuelle du temps immédiatement dans l'image supérieure, l'événement D peut être construit comme l'événement à x ′ = 0 (l'emplacement de l'horloge W 'dans S '), qui est simultané à C ( OC a un intervalle espace-temps égal à OA ) en S′. Cela montre que l'intervalle de temps OD est plus long que OA , ce qui montre que l'horloge "en mouvement" tourne plus lentement.
Dans l'image du bas, le repère S se déplace avec une vitesse − v dans le repère S′ au repos. La ligne d'univers de l'horloge W est l' axe ct (incliné vers la gauche), la ligne d'univers de W′ 1 est l'axe vertical ct ′ et la ligne d'univers de W′ 2 est la verticale passant par l'événement C , avec la coordonnée ct ′ D. _ L'hyperbole invariante passant par l'événement C met à l'échelle l'intervalle de temps OC à OA , qui est plus court que OD ; de plus, B est construit (similaire à D dans les images du haut) comme simultané à A dans S, à x = 0. Le résultat OB > OC correspond à nouveau à ci-dessus.
Le mot "mesurer" est important. En physique classique, un observateur ne peut pas affecter un objet observé, mais l'état de mouvement de l'objet peut affecter les observations de l'objet par l'observateur.
Paradoxe des jumeaux
De nombreuses introductions à la relativité restreinte illustrent les différences entre relativité galiléenne et relativité restreinte en posant une série de « paradoxes ». Ces paradoxes sont en fait des problèmes mal posés, résultant de notre méconnaissance des vitesses comparables à la vitesse de la lumière. Le remède consiste à résoudre de nombreux problèmes en relativité restreinte et à se familiariser avec ses prédictions dites contre-intuitives. L'approche géométrique de l'étude de l'espace-temps est considérée comme l'une des meilleures méthodes pour développer une intuition moderne.
Le paradoxe des jumeaux est une expérience de pensée impliquant des jumeaux identiques, dont l'un fait un voyage dans l'espace dans une fusée à grande vitesse, rentrant chez lui pour découvrir que le jumeau qui est resté sur Terre a plus vieilli. Ce résultat paraît déroutant car chaque jumeau observe l'autre comme bougeant, et donc à première vue, il semblerait que chacun devrait trouver que l'autre a moins vieilli. Le paradoxe des jumeaux évite la justification de la dilatation mutuelle du temps présentée ci-dessus en évitant l'exigence d'une troisième horloge. Néanmoins, le paradoxe des jumeaux n'est pas un vrai paradoxe car il est facile à comprendre dans le contexte de la relativité restreinte.
L'impression qu'un paradoxe existe découle d'une mauvaise compréhension de ce qu'énonce la relativité restreinte. La relativité restreinte ne déclare pas tous les cadres de référence comme étant équivalents, seulement les cadres inertiels. Le châssis du jumeau voyageur n'est pas inertiel pendant les périodes d'accélération. De plus, la différence entre les jumeaux est observable : la jumelle voyageuse doit tirer ses roquettes pour pouvoir rentrer chez elle, contrairement à la jumelle qui reste à la maison.
Ces distinctions devraient entraîner une différence d'âge entre les jumeaux. Le diagramme d'espace-temps de la figure 2-11 présente le cas simple d'un jumeau sortant tout droit le long de l'axe x et revenant immédiatement en arrière. Du point de vue du jumeau qui reste à la maison, il n'y a rien de déroutant dans le paradoxe des jumeaux. Le temps propre mesuré le long de la ligne d'univers du jumeau voyageur de O à C, plus le temps propre mesuré de C à B, est inférieur au temps propre du jumeau au foyer mesuré de O à A à B. Des trajectoires plus complexes nécessitent l'intégration le temps propre entre les événements respectifs le long de la courbe (c'est-à-dire l' intégrale de chemin ) pour calculer la quantité totale de temps propre vécue par le jumeau en déplacement.
Des complications surviennent si le paradoxe des jumeaux est analysé du point de vue du jumeau voyageur.
La nomenclature de Weiss, désignant le jumeau au foyer comme Terence et le jumeau voyageur comme Stella, est utilisée ci-après.
Stella n'est pas dans un référentiel inertiel. Compte tenu de ce fait, il est parfois indiqué à tort que la résolution complète du paradoxe des jumeaux nécessite la relativité générale :
Une analyse SR pure serait la suivante : Analysée dans le cadre de repos de Stella, elle est immobile pendant tout le trajet. Lorsqu'elle tire ses fusées pour le revirement, elle subit une pseudo-force qui ressemble à une force gravitationnelle. Figues. 2-6 et 2-11 illustrent le concept de lignes (plans) de simultanéité : les lignes parallèles à l' axe x de l'observateur (plan xy ) représentent des ensembles d'événements qui sont simultanés dans le cadre de l'observateur. Dans la Fig. 2-11, les lignes bleues relient les événements sur la ligne du monde de Terence qui, du point de vue de Stella , sont simultanés avec les événements sur sa ligne du monde. (Terence, à son tour, observerait un ensemble de lignes horizontales de simultanéité.) Tout au long des étapes aller et retour du voyage de Stella, elle mesure les horloges de Terence comme fonctionnant plus lentement que la sienne. Mais pendant le retournement (c'est-à-dire entre les lignes bleues en gras sur la figure), un décalage se produit dans l'angle de ses lignes de simultanéité, correspondant à un saut rapide des événements dans la ligne du monde de Terence que Stella considère comme simultanés avec sa propre. Ainsi, à la fin de son voyage, Stella constate que Terence a plus vieilli qu'elle.
Bien que la relativité générale ne soit pas nécessaire pour analyser le paradoxe des jumeaux, l'application du principe d'équivalence de la relativité générale fournit un aperçu supplémentaire du sujet. Stella n'est pas stationnaire dans un référentiel inertiel. Analysée dans le cadre de repos de Stella, elle est immobile pendant tout le trajet. Lorsqu'elle est en roue libre, son cadre de repos est inertiel et l'horloge de Terence semble fonctionner lentement. Mais lorsqu'elle tire ses fusées pour le retournement, son cadre de repos est un cadre accéléré et elle subit une force qui la pousse comme si elle était dans un champ gravitationnel. Terence semblera être haut placé dans ce domaine et en raison de la dilatation gravitationnelle du temps , son horloge semblera fonctionner rapidement, à tel point que le résultat net sera que Terence a plus vieilli que Stella lorsqu'ils seront de retour ensemble. Les arguments théoriques prédisant la dilatation gravitationnelle du temps ne sont pas exclusifs à la relativité générale. Toute théorie de la gravité prédira la dilatation gravitationnelle du temps si elle respecte le principe d'équivalence, y compris la théorie de Newton.
Gravitation
Cette section d'introduction s'est concentrée sur l'espace-temps de la relativité restreinte, car c'est le plus facile à décrire. L'espace-temps de Minkowski est plat, ne tient pas compte de la gravité, est uniforme partout et ne sert rien de plus qu'un arrière-plan statique pour les événements qui s'y déroulent. La présence de la gravité complique grandement la description de l'espace-temps. En relativité générale, l'espace-temps n'est plus un arrière-plan statique, mais interagit activement avec les systèmes physiques qu'il contient. Les courbes de l'espace-temps en présence de matière peuvent propager des ondes, plier la lumière et présenter une foule d'autres phénomènes. Quelques-uns de ces phénomènes sont décrits dans les sections suivantes de cet article.
Mathématiques de base de l'espace-temps
Transformations galiléennes
Un objectif fondamental est de pouvoir comparer les mesures effectuées par des observateurs en mouvement relatif. S'il y a un observateur O dans le cadre S qui a mesuré les coordonnées temporelles et spatiales d'un événement, attribuant à cet événement trois coordonnées cartésiennes et le temps mesuré sur son réseau d'horloges synchronisées ( x , y , z , t ) (voir Fig . 1-1 ). Un deuxième observateur O' dans un référentiel différent S' mesure le même événement dans son système de coordonnées et son réseau d'horloges synchronisées ( x ' , y ' , z ' , t ' ) . Avec les référentiels inertiels, aucun observateur n'est sous accélération, et un simple ensemble d'équations nous permet de relier les coordonnées ( x , y , z , t ) à ( x ′ , y ′ , z ′ , t ′ ) . Étant donné que les deux systèmes de coordonnées sont en configuration standard, c'est-à-dire qu'ils sont alignés avec des coordonnées parallèles ( x , y , z ) et que t = 0 lorsque t ′ = 0 , la transformation des coordonnées est la suivante :
La figure 3-1 montre que dans la théorie de Newton, le temps est universel, pas la vitesse de la lumière. Considérez l'expérience de pensée suivante : La flèche rouge illustre un train qui se déplace à 0,4 c par rapport au quai. A l'intérieur du train, un passager tire une balle avec une vitesse de 0,4 c dans le cadre du train. La flèche bleue illustre qu'une personne debout sur les voies ferrées mesure la balle comme se déplaçant à 0,8 c. Ceci est conforme à nos attentes naïves.
Plus généralement, en supposant que le référentiel S' se déplace à la vitesse v par rapport au référentiel S, alors dans le référentiel S', l'observateur O' mesure un objet se déplaçant à la vitesse u ' . La vitesse u par rapport au cadre S, puisque x = ut , x ′ = x − vt , et t = t ′ , peut être écrite comme x ′ = ut − vt = ( u − v ) t = ( u − v ) t " . Cela conduit à u ′ = x ′ / t ′ et finalement
- ou
qui est la loi galiléenne de sens commun pour l'addition des vitesses .
Composition relativiste des vitesses
La composition des vitesses est assez différente dans l'espace-temps relativiste. Pour réduire légèrement la complexité des équations, nous introduisons un raccourci commun pour le rapport de la vitesse d'un objet par rapport à la lumière,
La figure 3-2a illustre un train rouge qui avance à une vitesse donnée par v / c = β = s / a . Depuis le cadre amorcé du train, un passager tire une balle avec une vitesse donnée par u ′ / c = β ′ = n / m , où la distance est mesurée le long d'une ligne parallèle à l'axe rouge x ′ plutôt que parallèle à la axe x noir . Quelle est la vitesse composite u de la balle par rapport à la plate-forme, représentée par la flèche bleue ? En se référant à la Fig. 3-2b :
- Depuis la plate-forme, la vitesse composite de la balle est donnée par u = c ( s + r )/( a + b ) .
- Les deux triangles jaunes sont similaires car ce sont des triangles rectangles qui partagent un angle commun α . Dans le grand triangle jaune, le rapport s / a = v / c = β .
- Les rapports des côtés correspondants des deux triangles jaunes sont constants, de sorte que r / a = b / s = n / m = β ′ . Donc b = u ′ s / c et r = u ′ a / c .
- Remplacez les expressions de b et r dans l'expression de u à l'étape 1 pour obtenir la formule d'Einstein pour l'addition des vitesses :
La formule relativiste d'addition des vitesses présentée ci-dessus présente plusieurs caractéristiques importantes :
- Si u ′ et v sont tous les deux très petits devant la vitesse de la lumière, alors le produit vu ′ / c 2 devient infiniment petit, et le résultat global devient indiscernable de la formule de Galilée (formule de Newton) pour l'addition des vitesses : u = u ′ + v . La formule galiléenne est un cas particulier de la formule relativiste applicable aux faibles vitesses.
- Si u ′ est égal à c , alors la formule donne u = c quelle que soit la valeur de départ de v . La vitesse de la lumière est la même pour tous les observateurs, quels que soient leurs mouvements par rapport à la source émettrice.
Dilatation du temps et contraction de la longueur revisitées
Il est simple d'obtenir des expressions quantitatives pour la dilatation du temps et la contraction de la longueur. La figure 3-3 est une image composite contenant des images individuelles tirées de deux animations précédentes, simplifiées et réétiquetées pour les besoins de cette section.
Pour réduire légèrement la complexité des équations, il existe une variété de notations abrégées différentes pour ct :
- et sont communs.
- On voit aussi très fréquemment l'utilisation de la convention
Sur la Fig. 3-3a, les segments OA et OK représentent des intervalles d'espace-temps égaux. La dilatation du temps est représentée par le rapport OB / OK . L'hyperbole invariante a l'équation w = √ x 2 + k 2 où k = OK , et la ligne rouge représentant la ligne d'univers d'une particule en mouvement a l'équation w = x / β = xc / v . Un peu de manipulation algébrique donne
L'expression impliquant le symbole de la racine carrée apparaît très fréquemment en relativité, et un sur l'expression est appelé le facteur de Lorentz, désigné par la lettre grecque gamma :
Si v est supérieur ou égal à c , l'expression de devient physiquement dénuée de sens, ce qui implique que c est la vitesse maximale possible dans la nature. Pour tout v supérieur à zéro, le facteur de Lorentz sera supérieur à un, bien que la forme de la courbe soit telle que pour les basses vitesses, le facteur de Lorentz soit extrêmement proche de un.
Sur la Fig. 3-3b, les segments OA et OK représentent des intervalles d'espace-temps égaux. La contraction de la longueur est représentée par le rapport OB / OK . L'hyperbole invariante a l'équation x = √ w 2 + k 2 , où k = OK , et les bords de la bande bleue représentant les lignes d'univers des extrémités d'une tige en mouvement ont une pente 1/ β = c / v . L'événement A a pour coordonnées ( x , w ) = ( γk , γβk ). Puisque la droite tangente passant par A et B a pour équation w = ( x − OB )/ β , nous avons γβk = ( γk − OB )/ β et
Transformations de Lorentz
Les transformations galiléennes et leur loi de bon sens conséquente d'addition des vitesses fonctionnent bien dans notre monde ordinaire à basse vitesse d'avions, de voitures et de balles. Cependant, à partir du milieu des années 1800, des instruments scientifiques sensibles ont commencé à trouver des anomalies qui ne correspondaient pas bien à l'addition ordinaire des vitesses.
Les transformations de Lorentz sont utilisées pour transformer les coordonnées d'un événement d'un cadre à un autre en relativité restreinte.
Le facteur de Lorentz apparaît dans les transformations de Lorentz :
Les transformations inverses de Lorentz sont :
Lorsque v ≪ c et x est suffisamment petit, les termes v 2 / c 2 et vx / c 2 tendent vers zéro, et les transformations de Lorentz se rapprochent des transformations galiléennes.
etc., signifie le plus souvent vraiment etc. Bien que par souci de brièveté les équations de transformation de Lorentz soient écrites sans deltas, x signifie Δ x , etc. Nous sommes, en général, toujours concernés par les différences d'espace et de temps entre les événements.
Appeler un ensemble de transformations les transformations de Lorentz normales et l'autre les transformations inverses est trompeur, car il n'y a pas de différence intrinsèque entre les cadres. Différents auteurs appellent l'un ou l'autre ensemble de transformations l'ensemble "inverse". Les transformations directes et inverses sont trivialement liées les unes aux autres, puisque la trame S ne peut être qu'en marche avant ou arrière par rapport à S ' . Donc, inverser les équations implique simplement de changer les variables amorcées et non amorcées et de remplacer v par - v .
Exemple : Terence et Stella participent à une course spatiale Terre-Mars. Terence est un officiel sur la ligne de départ, tandis que Stella est une participante. Au temps t = t ′ = 0 , le vaisseau spatial de Stella accélère instantanément à une vitesse de 0,5 c . La distance de la Terre à Mars est de 300 secondes-lumière (environ90,0 × 10 6 km ). Terence observe Stella franchir l'horloge de la ligne d'arrivée à t = 600.00 s . Mais Stella observe l'heure sur son chronomètre de navire lorsqu'elle passe la ligne d'arrivée, et elle calcule la distance entre les lignes de départ et d'arrivée, telle que mesurée dans son cadre, à 259,81 secondes-lumière (environ77,9 × 10 6 km ). 1).
Dérivation des transformations de Lorentz
Il y a eu plusieurs dizaines de dérivations des transformations de Lorentz depuis le travail original d'Einstein en 1905, chacune avec son objectif particulier. Bien que la dérivation d'Einstein soit basée sur l'invariance de la vitesse de la lumière, il existe d'autres principes physiques qui peuvent servir de points de départ. En fin de compte, ces points de départ alternatifs peuvent être considérés comme des expressions différentes du principe sous-jacent de localité , qui stipule que l'influence qu'une particule exerce sur une autre ne peut pas être transmise instantanément.
La dérivation donnée ici et illustrée à la Fig. 3-5 est basée sur celle présentée par Bais et utilise les résultats précédents des sections Composition relativiste des vitesses, Dilatation du temps et Contraction de la longueur. L'événement P a des coordonnées ( w , x ) dans le "système de repos" noir et des coordonnées ( w ′ , x ′ ) dans le cadre rouge qui se déplace avec le paramètre de vitesse β = v / c . Pour déterminer w ′ et x ′ en termes de w et x (ou l'inverse), il est d'abord plus facile de dériver la transformation de Lorentz inverse .
- Il ne peut y avoir d'expansion/contraction de longueur dans les directions transversales. y ' doit être égal à y et z ' doit être égal à z , sinon le fait qu'une balle de 1 m se déplaçant rapidement puisse passer à travers un trou circulaire de 1 m dépend de l'observateur. Le premier postulat de la relativité stipule que tous les référentiels inertiels sont équivalents et que l'expansion/contraction transversale violerait cette loi.
- D'après le dessin, w = a + b et x = r + s
- D'après les résultats précédents utilisant des triangles similaires, nous savons que s / a = b / r = v / c = β .
- En raison de la dilatation du temps, a = γw ′
- La substitution de l'équation (4) dans s / a = β donne s = γw ′ β .
- La contraction de la longueur et les triangles similaires nous donnent r = γx ′ et b = βr = βγx ′
- La substitution des expressions pour s , a , r et b dans les équations de l'étape 2 donne immédiatement
Les équations ci-dessus sont des expressions alternatives pour les équations t et x de la transformation inverse de Lorentz, comme on peut le voir en substituant ct à w , ct ′ à w ′ et v / c à β . À partir de la transformation inverse, les équations de la transformation vers l'avant peuvent être dérivées en résolvant pour t ' et x ' .
Linéarité des transformations de Lorentz
Les transformations de Lorentz ont une propriété mathématique appelée linéarité, puisque x ′ et t ′ sont obtenus sous forme de combinaisons linéaires de x et t , sans aucune puissance supérieure impliquée. La linéarité de la transformation reflète une propriété fondamentale de l'espace-temps qui a été tacitement supposée dans la dérivation, à savoir que les propriétés des référentiels inertiels sont indépendantes de l'emplacement et du temps. En l'absence de gravité, l'espace-temps a le même aspect partout. Tous les observateurs inertiels s'accorderont sur ce qui constitue un mouvement accéléré et non accéléré. N'importe quel observateur peut utiliser ses propres mesures d'espace et de temps, mais il n'y a rien d'absolu à leur sujet. Les conventions d'un autre observateur feront tout aussi bien l'affaire.
Un résultat de la linéarité est que si deux transformations de Lorentz sont appliquées séquentiellement, le résultat est également une transformation de Lorentz.
Exemple : Terence observe Stella s'éloigner de lui à toute vitesse à 0,500 c , et il peut utiliser les transformations de Lorentz avec β = 0,500 pour relier les mesures de Stella aux siennes. Stella, dans son cadre, observe Ursula s'éloigner d'elle à 0,250 c , et elle peut utiliser les transformations de Lorentz avec β = 0,250 pour relier les mesures d'Ursula aux siennes. En raison de la linéarité des transformations et de la composition relativiste des vitesses, Terence peut utiliser les transformations de Lorentz avec β = 0,666 pour relier les mesures d'Ursula aux siennes.
effet Doppler
L' effet Doppler est le changement de fréquence ou de longueur d'onde d'une onde pour un récepteur et une source en mouvement relatif. Pour simplifier, nous considérons ici deux scénarios de base : (1) Les mouvements de la source et/ou du récepteur sont exactement le long de la ligne qui les relie (effet Doppler longitudinal), et (2) les mouvements sont perpendiculaires à ladite ligne ( effet Doppler transverse ). Nous ignorons les scénarios où ils se déplacent le long d'angles intermédiaires.
Effet Doppler longitudinal
L'analyse Doppler classique traite des ondes qui se propagent dans un milieu, telles que les ondes sonores ou les ondulations de l'eau, et qui sont transmises entre des sources et des récepteurs qui se rapprochent ou s'éloignent les uns des autres. L'analyse de ces ondes dépend du fait que la source, le récepteur ou les deux se déplacent par rapport au milieu. Etant donné le scénario où le récepteur est stationnaire par rapport au milieu, et la source s'éloigne directement du récepteur à une vitesse de v s pour un paramètre de vitesse de β s , la longueur d'onde est augmentée, et la fréquence observée f est donnée par
D'autre part, étant donné le scénario où la source est stationnaire, et le récepteur s'éloigne directement de la source à une vitesse de v r pour un paramètre de vitesse de β r , la longueur d'onde n'est pas modifiée, mais la vitesse de transmission des ondes par rapport au récepteur est diminuée, et la fréquence observée f est donnée par
La lumière, contrairement aux ondulations du son ou de l'eau, ne se propage pas à travers un milieu, et il n'y a pas de distinction entre une source s'éloignant du récepteur ou un récepteur s'éloignant de la source. La figure 3-6 illustre un diagramme d'espace-temps relativiste montrant une source se séparant du récepteur avec un paramètre de vitesse β , de sorte que la séparation entre la source et le récepteur au temps w est βw . En raison de la dilatation du temps, . Puisque la pente du rayon lumineux vert est −1, . Par conséquent, l' effet Doppler relativiste est donné par
Effet Doppler transverse
Supposons qu'une source et un récepteur, tous deux se rapprochant l'un de l'autre dans un mouvement d'inertie uniforme le long de lignes non sécantes, soient à leur approche la plus proche l'un de l'autre. Il semblerait que l'analyse classique prédise que le récepteur ne détecte aucun décalage Doppler. En raison des subtilités de l'analyse, cette attente n'est pas nécessairement vraie. Néanmoins, lorsqu'il est correctement défini, le décalage Doppler transverse est un effet relativiste qui n'a pas d'analogue classique. Les subtilités sont celles-ci :
Dans le scénario (a), le point d'approche le plus proche est indépendant du cadre et représente le moment où il n'y a pas de changement de distance en fonction du temps (c'est-à-dire dr/dt = 0 où r est la distance entre le récepteur et la source) et donc pas de Doppler longitudinal décalage. La source observe le récepteur comme étant éclairé par une lumière de fréquence f ' , mais observe également le récepteur comme ayant une horloge dilatée dans le temps. Dans la trame S, le récepteur est donc éclairé par une lumière décalée vers le bleu de fréquence
Dans le scénario (b), l'illustration montre le récepteur éclairé par la lumière à partir du moment où la source était la plus proche du récepteur, même si la source s'est déplacée. Parce que les horloges de la source sont dilatées dans le temps comme mesuré dans l'image S, et puisque dr/dt était égal à zéro à ce point, la lumière de la source, émise à partir de ce point le plus proche, est décalée vers le rouge avec la fréquence
Les scénarios (c) et (d) peuvent être analysés par de simples arguments de dilatation temporelle. En (c), le récepteur observe la lumière de la source comme décalée vers le bleu d'un facteur , et en (d), la lumière est décalée vers le rouge. La seule complication apparente est que les objets en orbite sont en mouvement accéléré. Cependant, si un observateur inertiel regarde une horloge en accélération, seule la vitesse instantanée de l'horloge est importante lors du calcul de la dilatation du temps. (L'inverse, cependant, n'est pas vrai.) La plupart des rapports de décalage Doppler transversal se réfèrent à l'effet comme un décalage vers le rouge et analysent l'effet en termes de scénarios (b) ou (d).
Énergie et élan
Étendre l'élan à quatre dimensions
En mécanique classique, l'état de mouvement d'une particule est caractérisé par sa masse et sa vitesse. La quantité de mouvement linéaire , produit de la masse et de la vitesse d'une particule, est une grandeur vectorielle , possédant la même direction que la vitesse : p = m v . C'est une quantité conservée , ce qui signifie que si un système fermé n'est pas affecté par des forces extérieures, sa quantité de mouvement linéaire totale ne peut pas changer.
En mécanique relativiste, le vecteur impulsion est étendu à quatre dimensions. Au vecteur d'impulsion s'ajoute une composante temporelle qui permet au vecteur d'impulsion de l'espace-temps de se transformer comme le vecteur de position de l'espace-temps . En explorant les propriétés de la quantité de mouvement de l'espace-temps, nous commençons, dans la Fig. 3-8a, par examiner à quoi ressemble une particule au repos. Dans le repère de repos, la composante spatiale de la quantité de mouvement est nulle, c'est-à-dire p = 0 , mais la composante temporelle est égale à mc .
Nous pouvons obtenir les composantes transformées de ce vecteur dans le référentiel mobile en utilisant les transformations de Lorentz, ou nous pouvons le lire directement sur la figure car nous savons que et , puisque les axes rouges sont redimensionnés par gamma. La figure 3-8b illustre la situation telle qu'elle apparaît dans le cadre mobile. Il est évident que les composantes d'espace et de temps des quatre impulsions tendent vers l'infini lorsque la vitesse du repère mobile approche de c .
Nous utiliserons ces informations sous peu pour obtenir une expression du quadri-momentum .
Moment de la lumière
Les particules de lumière, ou photons, se déplacent à la vitesse de c , la constante connue sous le nom de vitesse de la lumière . Cette affirmation n'est pas une tautologie, puisque de nombreuses formulations modernes de la relativité ne partent pas de la vitesse constante de la lumière comme postulat. Les photons se propagent donc le long d'une ligne d'univers semblable à la lumière et, dans des unités appropriées, ont des composantes spatiales et temporelles égales pour chaque observateur.
Une conséquence de la théorie de l'électromagnétisme de Maxwell est que la lumière transporte de l'énergie et de la quantité de mouvement, et que leur rapport est une constante : . En réarrangeant, , et puisque pour les photons, les composantes spatiale et temporelle sont égales, E/c doit donc être assimilé à la composante temporelle du vecteur impulsion espace-temps.
Les photons voyagent à la vitesse de la lumière, mais ont une quantité de mouvement et une énergie finies. Pour qu'il en soit ainsi, le terme de masse dans γmc doit être nul, ce qui signifie que les photons sont des particules sans masse . L'infini multiplié par zéro est une quantité mal définie, mais E/c est bien défini.
Par cette analyse, si l'énergie d'un photon est égale à E dans le référentiel au repos, elle est égale dans un référentiel en mouvement. Ce résultat peut être dérivé par inspection de la Fig. 3-9 ou par application des transformations de Lorentz, et est cohérent avec l'analyse de l'effet Doppler donnée précédemment.
Relation masse-énergie
La prise en compte des interrelations entre les différentes composantes du vecteur moment relativiste a conduit Einstein à plusieurs conclusions célèbres.
- Dans la limite de faible vitesse, lorsque β = v/c tend vers zéro, γ tend vers 1, la composante spatiale de la quantité de mouvement relativiste se rapproche donc de mv , le terme classique pour la quantité de mouvement. Dans cette perspective, γm peut être interprété comme une généralisation relativiste de m . Einstein a proposé que la masse relativiste d'un objet augmente avec la vitesse selon la formule .
- De même, en comparant la composante temporelle de la quantité de mouvement relativiste avec celle du photon, , de sorte qu'Einstein est arrivé à la relation . Simplifiée au cas de la vitesse nulle, c'est la célèbre équation d'Einstein reliant l'énergie et la masse.
Une autre façon d'examiner la relation entre la masse et l'énergie est de considérer un développement en série de γmc 2 à faible vitesse :
Le deuxième terme est juste une expression de l'énergie cinétique de la particule. La masse apparaît en effet comme une autre forme d'énergie.
Le concept de masse relativiste qu'Einstein a introduit en 1905, m rel , bien que largement validé chaque jour dans les accélérateurs de particules du monde entier (ou d'ailleurs dans toute instrumentation dont l'utilisation dépend de particules à grande vitesse, comme les microscopes électroniques, les téléviseurs couleur à l'ancienne , etc.), ne s'est pourtant pas avéré être un concept fécond en physique dans le sens où ce n'est pas un concept qui a servi de base à d'autres développements théoriques. La masse relativiste, par exemple, ne joue aucun rôle dans la relativité générale.
Pour cette raison, ainsi que pour des raisons pédagogiques, la plupart des physiciens préfèrent actuellement une terminologie différente lorsqu'ils se réfèrent à la relation entre la masse et l'énergie. "Masse relativiste" est un terme obsolète. Le terme «masse» en lui-même fait référence à la masse au repos ou à la masse invariante et est égal à la longueur invariante du vecteur moment relativiste. Exprimé sous forme de formule,
Cette formule s'applique à toutes les particules, sans masse comme massives. Pour les photons où m rest est égal à zéro, cela donne, .
Quatre élans
En raison de la relation étroite entre la masse et l'énergie, le quatre-momentum (également appelé 4-momentum) est également appelé le vecteur énergie-momentum 4. En utilisant un P majuscule pour représenter les quatre impulsions et un p minuscule pour désigner l'impulsion spatiale, les quatre impulsions peuvent être écrites comme
- Ou bien,
- en utilisant la convention que
Lois de conservation
En physique, les lois de conservation stipulent que certaines propriétés mesurables particulières d'un système physique isolé ne changent pas à mesure que le système évolue dans le temps. En 1915, Emmy Noether a découvert que sous-jacente à chaque loi de conservation se trouve une symétrie fondamentale de la nature. Le fait que les processus physiques ne se soucient pas de l' endroit où ils se déroulent dans l'espace ( symétrie de translation spatiale ) donne la conservation de la quantité de mouvement , le fait que de tels processus ne se soucient pas du moment où ils se produisent ( symétrie de translation temporelle ) donne la conservation de l'énergie , et ainsi sur. Dans cette section, nous examinons les conceptions newtoniennes de la conservation de la masse, de la quantité de mouvement et de l'énergie dans une perspective relativiste.
Momentum total
Pour comprendre comment la vision newtonienne de la conservation de la quantité de mouvement doit être modifiée dans un contexte relativiste, nous examinons le problème de la collision de deux corps limité à une seule dimension.
En mécanique newtonienne, deux cas extrêmes de ce problème peuvent être distingués donnant des mathématiques de complexité minimale :
- (1) Les deux corps rebondissent l'un sur l'autre dans une collision complètement élastique.
- (2) Les deux corps se collent et continuent à se déplacer comme une seule particule. Ce deuxième cas est le cas d'une collision complètement inélastique.
Dans les deux cas (1) et (2), la quantité de mouvement, la masse et l'énergie totale sont conservées. Cependant, l'énergie cinétique n'est pas conservée en cas de collision inélastique. Une certaine fraction de l'énergie cinétique initiale est convertie en chaleur.
Dans le cas (2), deux masses avec des moments et entrent en collision pour produire une seule particule de masse conservée se déplaçant au centre de la vitesse de masse du système d'origine, . La quantité de mouvement totale est conservée.
La figure 3-10 illustre la collision inélastique de deux particules dans une perspective relativiste. Les composantes temporelles et s'ajoutent au total E/c du vecteur résultant, ce qui signifie que l'énergie est conservée. De même, les composantes spatiales et s'additionnent pour former p du vecteur résultant. Le quatre-momentum est, comme prévu, une quantité conservée. Cependant, la masse invariante de la particule fusionnée, donnée par le point où l'hyperbole invariante de la quantité de mouvement totale coupe l'axe de l'énergie, n'est pas égale à la somme des masses invariantes des particules individuelles qui sont entrées en collision. En effet, elle est supérieure à la somme des masses individuelles : .
En regardant les événements de ce scénario dans l'ordre inverse, nous voyons que la non-conservation de la masse est un phénomène courant : lorsqu'une particule élémentaire instable se désintègre spontanément en deux particules plus légères, l'énergie totale est conservée, mais pas la masse. Une partie de la masse est convertie en énergie cinétique.
Choix des référentiels
La liberté de choisir n'importe quel cadre dans lequel effectuer une analyse nous permet d'en choisir un qui peut être particulièrement pratique. Pour l'analyse des problèmes de quantité de mouvement et d'énergie, le cadre le plus pratique est généralement le « cadre du centre de la quantité de mouvement » (également appelé cadre à impulsion nulle ou cadre COM). C'est le référentiel dans lequel la composante spatiale de la quantité de mouvement totale du système est nulle. La figure 3-11 illustre la décomposition d'une particule à grande vitesse en deux particules filles. Dans le cadre du laboratoire, les particules filles sont préférentiellement émises dans une direction orientée le long de la trajectoire de la particule d'origine. Dans le cadre COM, cependant, les deux particules filles sont émises dans des directions opposées, bien que leurs masses et l'amplitude de leurs vitesses ne soient généralement pas les mêmes.
Conservation de l'énergie et de la quantité de mouvement
Dans une analyse newtonienne de particules en interaction, la transformation entre référentiels est simple car il suffit d'appliquer la transformation galiléenne à toutes les vitesses. Depuis , l' élan . Si l'on observe que la quantité de mouvement totale d'un système de particules en interaction est conservée dans un référentiel, on observera également qu'elle est conservée dans n'importe quel autre référentiel.
La conservation de la quantité de mouvement dans le cadre COM équivaut à l'exigence que p = 0 à la fois avant et après la collision. Dans l'analyse newtonienne, la conservation de la masse dicte que . Dans les scénarios unidimensionnels simplifiés que nous avons envisagés, une seule contrainte supplémentaire est nécessaire avant que l'impulsion sortante des particules puisse être déterminée : une condition d'énergie. Dans le cas unidimensionnel d'une collision complètement élastique sans perte d'énergie cinétique, les vitesses sortantes des particules rebondissantes dans le cadre COM seront précisément égales et opposées à leurs vitesses entrantes. Dans le cas d'une collision complètement inélastique avec perte totale d'énergie cinétique, les vitesses sortantes des particules rebondissantes seront nulles.
Les moments newtoniens, calculés comme , ne se comportent pas correctement sous la transformation lorentzienne. La transformation linéaire des vitesses est remplacée par la transformation hautement non linéaire de sorte qu'un calcul démontrant la conservation de la quantité de mouvement dans un cadre sera invalide dans d'autres cadres. Einstein devait soit renoncer à la conservation de la quantité de mouvement, soit changer la définition de la quantité de mouvement. C'est cette deuxième option qu'il a choisie.
La loi de conservation relativiste de l'énergie et de la quantité de mouvement remplace les trois lois de conservation classiques de l'énergie, de la quantité de mouvement et de la masse. La masse n'est plus conservée de manière indépendante, car elle a été subsumée dans l'énergie relativiste totale. Cela fait de la conservation relativiste de l'énergie un concept plus simple que dans la mécanique non relativiste, car l'énergie totale est conservée sans aucune qualification. L'énergie cinétique convertie en chaleur ou en énergie potentielle interne se traduit par une augmentation de la masse.
La figure 3-12a illustre le diagramme énergie-impulsion de cette réaction de désintégration dans le cadre de repos du pion. En raison de sa masse négligeable, un neutrino se déplace à une vitesse très proche de la lumière. L'expression relativiste de son énergie, comme celle du photon, est qui est aussi la valeur de la composante spatiale de sa quantité de mouvement. Pour conserver l'impulsion, le muon a la même valeur que la composante spatiale de l'impulsion du neutrino, mais dans le sens opposé.
Des analyses algébriques de l'énergétique de cette réaction de désintégration sont disponibles en ligne, donc la Fig. 3-12b présente à la place une solution de calculatrice graphique. L'énergie du neutrino est de 29,79 MeV et l'énergie du muon est de 33,91 MeV − 29,79 MeV = 4,12 MeV . La majeure partie de l'énergie est emportée par le neutrino de masse quasi nulle.Au-delà des bases
Les sujets de cette section sont d'une difficulté technique nettement plus grande que ceux des sections précédentes et ne sont pas essentiels pour comprendre Introduction à l'espace-temps courbe.
Rapidité
Les transformations de Lorentz relient les coordonnées des événements d'un référentiel à celles d'un autre référentiel. La composition relativiste des vitesses est utilisée pour additionner deux vitesses ensemble. Les formules pour effectuer ces derniers calculs sont non linéaires, ce qui les rend plus complexes que les formules galiléennes correspondantes.
Cette non-linéarité est un artefact de notre choix de paramètres. Nous avons précédemment noté que dans un diagramme d'espace-temps x – ct , les points à un intervalle d'espace-temps constant à partir de l'origine forment une hyperbole invariante. Nous avons également noté que les systèmes de coordonnées de deux référentiels d'espace-temps en configuration standard sont en rotation hyperbolique l'un par rapport à l'autre.
Les fonctions naturelles pour exprimer ces relations sont les analogues hyperboliques des fonctions trigonométriques . La figure 4-1a montre un cercle unitaire avec sin( a ) et cos( a ), la seule différence entre ce diagramme et le cercle unitaire familier de la trigonométrie élémentaire étant que a est interprété, et non comme l'angle entre le rayon et le x -axis , mais comme deux fois la surface du secteur balayé par le rayon à partir de l' x -axis . (Numériquement, les mesures d'angle et de surface 2 × pour le cercle unitaire sont identiques.) La figure 4-1b montre une hyperbole unitaire avec sinh( a ) et cosh( a ), où a est également interprété comme le double de la surface teintée. La Fig. 4-2 présente les tracés des fonctions sinh, cosh et tanh.
Pour le cercle unitaire, la pente du rayon est donnée par
Dans le plan cartésien, la rotation du point ( x , y ) en point ( x ' , y ' ) d'angle θ est donnée par
Dans un diagramme espace-temps, le paramètre de vitesse est l'analogue de la pente. La rapidité , φ , est définie par
où
La rapidité définie ci-dessus est très utile en relativité restreinte car de nombreuses expressions prennent une forme considérablement plus simple lorsqu'elles sont exprimées en termes de celle-ci. Par exemple, la rapidité est simplement additive dans la formule d'addition de vitesse colinéaire ;
ou en d'autres termes,
Les transformations de Lorentz prennent une forme simple lorsqu'elles sont exprimées en termes de rapidité. Le facteur γ peut être écrit comme
Les transformations décrivant un mouvement relatif avec une vitesse uniforme et sans rotation des axes de coordonnées spatiales sont appelées boosts .
En remplaçant γ et γβ dans les transformations présentées précédemment et en réécrivant sous forme matricielle, le boost de Lorentz dans la direction x peut s'écrire
et le boost de Lorentz inverse dans la direction x peut être écrit comme
En d'autres termes, les boosts de Lorentz représentent des rotations hyperboliques dans l'espace-temps de Minkowski.
Les avantages de l'utilisation des fonctions hyperboliques sont tels que certains manuels comme les classiques de Taylor et Wheeler introduisent très tôt leur utilisation.
4 vecteurs
Quatre vecteurs ont été mentionnés ci-dessus dans le contexte du 4 vecteur énergie-impulsion , mais sans trop insister. En effet, aucune des dérivations élémentaires de la relativité restreinte ne les requiert. Mais une fois compris, les 4‑vecteurs , et plus généralement les tenseurs , simplifient grandement la compréhension mathématique et conceptuelle de la relativité restreinte. Travailler exclusivement avec de tels objets conduit à des formules manifestement invariantes relativistes, ce qui est un avantage considérable dans des contextes non triviaux. Par exemple, démontrer l'invariance relativiste des équations de Maxwell dans leur forme habituelle n'est pas trivial, alors qu'il ne s'agit que d'un calcul de routine (en réalité rien de plus qu'une observation) utilisant la formulation du tenseur d'intensité de champ . D'autre part, la relativité générale, dès le départ, s'appuie fortement sur les 4‑vecteurs , et plus généralement les tenseurs, représentant des entités physiquement pertinentes. Les relier via des équations qui ne reposent pas sur des coordonnées spécifiques nécessite des tenseurs, capables de connecter ces 4 vecteurs même dans un espace-temps courbe , et pas seulement dans un espace-temps plat comme dans la relativité restreinte. L'étude des tenseurs sort du cadre de cet article, qui ne fournit qu'une discussion de base sur l'espace-temps.
Définition des 4-vecteurs
Un 4-uplet est un "4-vecteur" si sa composante A i se transforme entre les trames selon la transformation de Lorentz.
Si vous utilisez des coordonnées, A est un vecteur 4 s'il se transforme (dans la direction x ) selon
qui vient du simple remplacement de ct par A 0 et x par A 1 dans la présentation précédente de la transformation de Lorentz.
Comme d'habitude, quand on écrit x , t , etc. on entend généralement Δx , Δt etc.
Les trois dernières composantes d'un vecteur 4 doivent être un vecteur standard dans un espace tridimensionnel. Par conséquent, un vecteur 4 doit se transformer comme sous les transformations de Lorentz ainsi que les rotations.
Propriétés des 4-vecteurs
- Fermeture sous combinaison linéaire : Si A et B sont 4-vecteurs , alors est aussi un 4-vecteur .
- Invariance du produit interne : Si A et B sont 4-vecteurs , alors leur produit interne (produit scalaire) est invariant, c'est-à-dire que leur produit interne est indépendant du référentiel dans lequel il est calculé. Notez comment le calcul du produit scalaire diffère du calcul du produit scalaire d'un 3-vecteur . Dans la suite, et sont des 3-vecteurs :
- En plus d'être invariant sous la transformation de Lorentz, le produit interne ci-dessus est également invariant sous rotation dans l'espace 3 .
- Deux vecteurs sont dits orthogonaux si Contrairement au cas des 3 vecteurs, les 4 vecteurs orthogonaux ne sont pas nécessairement à angle droit l'un par rapport à l'autre. La règle est que deux 4-vecteurs sont orthogonaux s'ils sont décalés d'angles égaux et opposés par rapport à la ligne à 45° qui est la ligne d'univers d'un rayon lumineux. Cela implique qu'un 4-vecteur léger est orthogonal à lui- même .
- Invariance de l'amplitude d'un vecteur : l'amplitude d'un vecteur est le produit intérieur d'un vecteur 4 avec lui-même et est une propriété indépendante du cadre. Comme pour les intervalles, la magnitude peut être positive, négative ou nulle, de sorte que les vecteurs sont appelés temporels, spatiaux ou nuls (lightlike). Notez qu'un vecteur nul n'est pas la même chose qu'un vecteur nul. Un vecteur nul est celui pour lequel tandis qu'un vecteur nul est celui dont les composantes sont toutes nulles. Les cas particuliers illustrant l'invariance de la norme incluent l'intervalle invariant et la longueur invariante du vecteur moment relativiste
Exemples de 4-vecteurs
- Déplacement 4-vecteur : autrement connu sous le nom de séparation de l'espace -temps , il s'agit de ( Δt, Δx, Δy, Δz ), ou pour les séparations infinitésimales, ( dt, dx, dy, dz ) .
- Velocity 4-vector : Cela se produit lorsque le déplacement 4-vector est divisé par , où est le temps propre entre les deux événements qui donnent dt, dx, dy et dz .
- La 4-vitesse est tangente à la ligne d'univers d'une particule et a une longueur égale à une unité de temps dans le cadre de la particule.
- Une particule accélérée n'a pas de référentiel inertiel dans lequel elle est toujours au repos. Cependant, un cadre inertiel peut toujours être trouvé qui se déplace momentanément avec la particule. Ce cadre, le cadre de référence momentanément comoving (MCRF), permet d'appliquer la relativité restreinte à l'analyse des particules accélérées.
- Puisque les photons se déplacent sur des lignes nulles, pour un photon, et une 4-vitesse ne peut pas être définie. Il n'y a pas de cadre dans lequel un photon est au repos, et aucun MCRF ne peut être établi le long du chemin d'un photon.
- Énergie-momentum 4-vecteur :
- Comme indiqué précédemment, il existe différents traitements pour le vecteur énergie-impulsion 4 de sorte que l'on peut également le voir exprimé en ou La première composante est l'énergie totale (y compris la masse) de la particule (ou du système de particules) dans un cadre donné , tandis que les composants restants sont son élan spatial. Le 4-vecteur énergie-impulsion est une quantité conservée.
- Accélération 4-vecteur : Cela résulte de la dérivée du 4-vecteur vitesse par rapport à
- Vecteur de force 4 : C'est la dérivée du vecteur de moment 4 par rapport à
Comme prévu, les composants finaux des 4 vecteurs ci- dessus sont tous des 3 vecteurs standard correspondant à l' impulsion spatiale 3 , à la force 3, etc.
4-vecteurs et loi physique
Le premier postulat de la relativité restreinte déclare l'équivalence de tous les référentiels inertiels. Une loi physique tenant dans un cadre doit s'appliquer à tous les cadres, car sinon il serait possible de différencier les cadres. Les impulsions newtoniennes ne se comportent pas correctement sous la transformation lorentzienne, et Einstein a préféré changer la définition de l'impulsion en une impliquant 4 vecteurs plutôt que d'abandonner la conservation de l'impulsion.
Les lois physiques doivent être basées sur des constructions indépendantes du cadre. Cela signifie que les lois physiques peuvent prendre la forme d'équations reliant des scalaires, qui sont toujours indépendants du cadre. Cependant, les équations impliquant 4 vecteurs nécessitent l'utilisation de tenseurs de rang approprié, qui eux-mêmes peuvent être considérés comme étant construits à partir de 4 vecteurs .
Accélération
C'est une idée fausse courante que la relativité restreinte ne s'applique qu'aux référentiels inertiels et qu'elle est incapable de gérer des objets en accélération ou des référentiels en accélération. En fait, les objets en accélération peuvent généralement être analysés sans avoir à traiter du tout avec des images en accélération. Ce n'est que lorsque la gravitation est significative que la relativité générale est nécessaire.
Cependant, la gestion correcte des images en accélération nécessite une certaine prudence. La différence entre la relativité restreinte et la relativité générale est que (1) Dans la relativité restreinte, toutes les vitesses sont relatives, mais l'accélération est absolue. (2) En relativité générale, tout mouvement est relatif, qu'il soit inertiel, en accélération ou en rotation. Pour tenir compte de cette différence, la relativité générale utilise un espace-temps courbe.
Dans cette section, nous analysons plusieurs scénarios impliquant des référentiels accélérés.
Paradoxe du vaisseau spatial Dewan – Beran – Bell
Le paradoxe du vaisseau spatial Dewan – Beran – Bell (paradoxe du vaisseau spatial de Bell ) est un bon exemple d'un problème où un raisonnement intuitif non assisté par la perspicacité géométrique de l'approche de l'espace-temps peut conduire à des problèmes.
Dans la Fig. 4-4, deux vaisseaux spatiaux identiques flottent dans l'espace et sont au repos l'un par rapport à l'autre. Ils sont reliés par une ficelle qui n'est capable que d'un étirement limité avant de se rompre. A un instant donné dans notre référentiel, le référentiel de l'observateur, les deux vaisseaux spatiaux accélèrent dans la même direction le long de la ligne qui les sépare avec la même accélération propre constante. La corde va-t-elle casser ?
Lorsque le paradoxe était nouveau et relativement inconnu, même les physiciens professionnels avaient du mal à trouver la solution. Deux lignes de raisonnement conduisent à des conclusions opposées. Les deux arguments, qui sont présentés ci-dessous, sont erronés même si l'un d'eux donne la bonne réponse.
- Pour les observateurs dans le cadre de repos, les vaisseaux spatiaux commencent à une distance L l'un de l' autre et restent à la même distance l'un de l'autre pendant l'accélération. Lors de l'accélération, L est une distance contractée en longueur de la distance L ' = γL dans le cadre des vaisseaux spatiaux en accélération. Après un temps suffisamment long, γ augmentera jusqu'à un facteur suffisamment grand pour que la corde doive casser.
- Soit A et B les vaisseaux spatiaux arrière et avant. Dans le cadre des vaisseaux spatiaux, chaque vaisseau spatial voit l'autre vaisseau spatial faire la même chose qu'il est en train de faire. A dit que B a la même accélération que lui, et B voit que A lui correspond à chaque mouvement. Ainsi, les vaisseaux spatiaux restent à la même distance et la ficelle ne se casse pas.
Le problème avec le premier argument est qu'il n'y a pas de "cadre des vaisseaux spatiaux". Il ne peut pas y en avoir, car les deux vaisseaux spatiaux mesurent une distance croissante entre les deux. Parce qu'il n'y a pas de cadre commun aux vaisseaux spatiaux, la longueur de la chaîne est mal définie. Néanmoins, la conclusion est correcte et l'argument est généralement juste. Le deuxième argument, cependant, ignore complètement la relativité de la simultanéité.
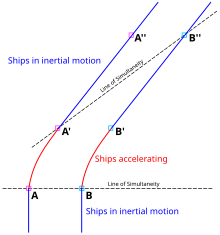
Un diagramme de l'espace-temps (Fig. 4-5) rend la solution correcte à ce paradoxe presque immédiatement évidente. Deux observateurs dans l'espace-temps de Minkowski accélèrent avec une accélération de magnitude constante pendant un temps propre (accélération et temps écoulé mesurés par les observateurs eux-mêmes, et non par un observateur inertiel). Ils sont mobiles et inertiels avant et après cette phase. En géométrie de Minkowski, la longueur le long de la ligne de simultanéité s'avère supérieure à la longueur le long de la ligne de simultanéité .
L'augmentation de longueur peut être calculée à l'aide de la transformation de Lorentz. Si, comme illustré à la Fig. 4-5, l'accélération est terminée, les navires resteront à un décalage constant dans une trame Si et sont les positions des navires dans les positions dans la trame sont :
Le « paradoxe », pour ainsi dire, vient de la façon dont Bell a construit son exemple. Dans la discussion habituelle de la contraction de Lorentz, la longueur de repos est fixe et la longueur de déplacement se raccourcit telle que mesurée dans le cadre . Comme le montre la figure 4-5, l'exemple de Bell affirme que les longueurs mobiles et mesurées dans l'image doivent être fixes, forçant ainsi la longueur de l'image restante dans l'image à augmenter.
Observateur accéléré avec horizon
Certaines configurations de problèmes de relativité restreinte peuvent conduire à un aperçu des phénomènes normalement associés à la relativité générale, tels que les horizons des événements . Dans le texte accompagnant la Fig. 2-7 , les hyperboles magenta représentaient des trajectoires réelles suivies par un voyageur en accélération constante dans l'espace-temps. Pendant les périodes d'accélération positive, la vitesse du voyageur s'approche juste de la vitesse de la lumière, tandis que, mesurée dans notre référentiel, l'accélération du voyageur diminue constamment.
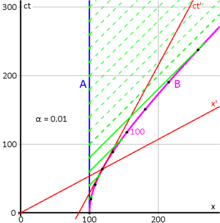
La figure 4-6 détaille diverses caractéristiques des mouvements du voyageur avec plus de précision. A tout moment, son axe spatial est formé par une ligne passant par l'origine et sa position actuelle sur l'hyperbole, tandis que son axe temporel est la tangente à l'hyperbole à sa position. Le paramètre de vitesse s'approche d'une limite de un à mesure qu'il augmente. De même, se rapproche de l'infini.
La forme de l'hyperbole invariante correspond à une trajectoire d'accélération propre constante. Ceci est démontrable comme suit :
- On s'en souvient
- Puisque nous concluons que
- De la loi de force relativiste,
- La substitution de l'étape 2 et l'expression de l'étape 3 donne qui est une expression constante.
La Fig. 4-6 illustre un scénario calculé spécifique. Terence (A) et Stella (B) se tiennent initialement ensemble à 100 heures-lumière de l'origine. Stella décolle au temps 0, son vaisseau spatial accélérant à 0,01 c par heure. Toutes les vingt heures, Terence fait le point par radio avec Stella sur la situation à la maison (lignes vertes pleines). Stella reçoit ces transmissions régulières, mais la distance croissante (compensée en partie par la dilatation du temps) l'amène à recevoir les communications de Terence de plus en plus tard, comme mesuré sur son horloge, et elle ne reçoit jamais de communications de Terence après 100 heures sur son horloge (pointillé vert lignes).
Après 100 heures selon l'horloge de Terence, Stella entre dans une région sombre. Elle a voyagé en dehors du futur temporel de Terence. En revanche, Terence peut continuer à recevoir indéfiniment les messages que Stella lui adresse. Il n'a qu'à attendre assez longtemps. L'espace-temps a été divisé en régions distinctes séparées par un horizon d'événements apparent . Tant que Stella continue d'accélérer, elle ne peut jamais savoir ce qui se passe derrière cet horizon.
Introduction à l'espace-temps courbe
Propositions de base
Les théories de Newton supposaient que le mouvement se produisait dans le contexte d'un cadre de référence euclidien rigide qui s'étendait à travers tout l'espace et tout le temps. La gravité est médiatisée par une force mystérieuse, agissant instantanément à distance, dont les actions sont indépendantes de l'espace intermédiaire. En revanche, Einstein a nié qu'il existe un cadre de référence euclidien d'arrière-plan qui s'étend dans tout l'espace. Il n'y a pas non plus de force de gravitation, seulement la structure de l'espace-temps lui-même.
En termes d'espace-temps, la trajectoire d'un satellite en orbite autour de la Terre n'est pas dictée par les influences lointaines de la Terre, de la Lune et du Soleil. Au lieu de cela, le satellite se déplace dans l'espace uniquement en réponse aux conditions locales. Puisque l'espace-temps est partout localement plat lorsqu'il est considéré à une échelle suffisamment petite, le satellite suit toujours une ligne droite dans son référentiel inertiel local. On dit que le satellite suit toujours la trajectoire d'une géodésique . Aucune preuve de gravitation ne peut être découverte en suivant les mouvements d'une seule particule.
Dans toute analyse de l'espace-temps, la preuve de la gravitation exige que l'on observe les accélérations relatives de deux corps ou de deux particules séparées. Dans la Fig. 5-1, deux particules séparées, en chute libre dans le champ gravitationnel de la Terre, présentent des accélérations de marée dues à des inhomogénéités locales dans le champ gravitationnel telles que chaque particule suit un chemin différent dans l'espace-temps. Les accélérations de marée que ces particules présentent les unes par rapport aux autres ne nécessitent pas de forces pour leur explication. Au contraire, Einstein les a décrits en termes de géométrie de l'espace-temps, c'est-à-dire la courbure de l'espace-temps. Ces accélérations de marée sont strictement locales. C'est l'effet total cumulé de nombreuses manifestations locales de courbure qui se traduisent par l' apparition d'une force gravitationnelle agissant à une longue distance de la Terre.
Deux propositions centrales sous-tendent la relativité générale.
- Le premier concept crucial est l'indépendance des coordonnées : les lois de la physique ne peuvent pas dépendre du système de coordonnées utilisé. Il s'agit d'une extension majeure du principe de relativité à partir de la version utilisée dans la relativité restreinte, qui stipule que les lois de la physique doivent être les mêmes pour chaque observateur se déplaçant dans des référentiels non accélérés (inertiel). En relativité générale, pour reprendre les propres mots d'Einstein (traduits), "les lois de la physique doivent être d'une nature telle qu'elles s'appliquent aux systèmes de référence dans tout type de mouvement". Cela conduit à un problème immédiat : dans les cadres accélérés, on ressent des forces qui apparemment permettraient d'évaluer son état d'accélération dans un sens absolu. Einstein a résolu ce problème grâce au principe d'équivalence.
- Le principe d'équivalence stipule que dans toute région suffisamment petite de l'espace, les effets de la gravitation sont les mêmes que ceux de l'accélération.
- Dans la Fig. 5-2, la personne A se trouve dans un vaisseau spatial, loin de tout objet massif, qui subit une accélération uniforme de g . La personne B est dans une boîte posée sur Terre. À condition que le vaisseau spatial soit suffisamment petit pour que les effets de marée ne soient pas mesurables (étant donné la sensibilité de l'instrumentation de mesure de la gravité actuelle, A et B devraient probablement être des lilliputiens ), il n'y a aucune expérience que A et B peuvent effectuer qui leur permettra de dire dans quel cadre ils se trouvent.
- Une expression alternative du principe d'équivalence est de noter que dans la loi universelle de la gravitation de Newton, F = GMm g /r 2 = m g g et dans la deuxième loi de Newton, F = m i a , il n'y a pas de raison a priori pour laquelle la force gravitationnelle la masse m g doit être égale à la masse d'inertie m i . Le principe d'équivalence stipule que ces deux masses sont identiques.
Pour passer de la description élémentaire ci-dessus de l'espace-temps courbe à une description complète de la gravitation, il faut du calcul tensoriel et de la géométrie différentielle, sujets qui nécessitent tous deux une étude considérable. Sans ces outils mathématiques, il est possible d'écrire sur la relativité générale, mais il n'est pas possible de démontrer des dérivations non triviales.
Courbure du temps
Dans le débat sur la relativité restreinte, les forces n'ont joué qu'un rôle d'arrière-plan. La relativité restreinte suppose la capacité de définir des cadres inertiels qui remplissent tout l'espace-temps, dont toutes les horloges fonctionnent au même rythme que l'horloge à l'origine. Est-ce vraiment possible ? Dans un champ gravitationnel non uniforme, l'expérience dicte que la réponse est non. Les champs gravitationnels rendent impossible la construction d'un référentiel inertiel global . Dans des régions suffisamment petites de l'espace-temps, des référentiels inertiels locaux sont encore possibles. La relativité générale implique l'assemblage systématique de ces cadres locaux dans une image plus générale de l'espace-temps.
Des années avant la publication de la théorie générale en 1916, Einstein a utilisé le principe d'équivalence pour prédire l'existence du redshift gravitationnel dans l' expérience de pensée suivante : (i) Supposons qu'une tour de hauteur h (Fig. 5-3) ait été construite. (ii) Laisser tomber une particule de masse au repos m du haut de la tour. Il tombe librement avec une accélération g , atteignant le sol avec une vitesse v = (2 gh ) 1/2 , de sorte que son énergie totale E , mesurée par un observateur au sol, est (iii) Un convertisseur masse-énergie transforme l'énergie totale l'énergie de la particule en un seul photon de haute énergie, qu'il dirige vers le haut. (iv) Au sommet de la tour, un convertisseur énergie-masse retransforme l'énergie du photon E ' en une particule de masse au repos m ' .
Il faut que m = m ' , car sinon on pourrait construire un dispositif à mouvement perpétuel . Nous prédisons donc que E ' = m , de sorte que
Un photon grimpant dans le champ gravitationnel de la Terre perd de l'énergie et est décalé vers le rouge. Les premières tentatives pour mesurer ce décalage vers le rouge par des observations astronomiques n'ont pas été concluantes, mais des observations définitives en laboratoire ont été effectuées par Pound & Rebka (1959) et plus tard par Pound & Snider (1964).
La lumière a une fréquence associée, et cette fréquence peut être utilisée pour piloter le fonctionnement d'une horloge. Le redshift gravitationnel conduit à une conclusion importante sur le temps lui-même : la gravité ralentit le temps. Supposons que nous construisions deux horloges identiques dont les fréquences sont contrôlées par une transition atomique stable. Placez une horloge au sommet de la tour, tandis que l'autre horloge reste au sol. Un expérimentateur au sommet de la tour observe que les signaux de l'horloge au sol ont une fréquence inférieure à celle de l'horloge à côté d'elle sur la tour. La lumière qui monte dans la tour n'est qu'une vague, et il est impossible que les crêtes des vagues disparaissent en montant. Exactement autant d'oscillations lumineuses arrivent au sommet de la tour qu'il en est émis en bas. L'expérimentateur conclut que l'horloge au sol est lente et peut le confirmer en abaissant l'horloge de la tour pour la comparer côte à côte avec l'horloge au sol. Pour une tour de 1 km, l'écart s'élèverait à environ 9,4 nanosecondes par jour, facilement mesurable avec l'instrumentation moderne.
Les horloges dans un champ gravitationnel ne fonctionnent pas toutes au même rythme. Des expériences telles que l'expérience Pound-Rebka ont fermement établi la courbure de la composante temporelle de l'espace-temps. L'expérience Pound-Rebka ne dit rien sur la courbure de la composante spatiale de l'espace -temps. Mais les arguments théoriques prédisant la dilatation gravitationnelle du temps ne dépendent pas du tout des détails de la relativité générale. Toute théorie de la gravité prédira la dilatation gravitationnelle du temps si elle respecte le principe d'équivalence. Cela inclut la gravitation newtonienne. Une démonstration standard en relativité générale est de montrer comment, dans la " limite newtonienne " (c'est-à-dire que les particules se déplacent lentement, le champ gravitationnel est faible et le champ est statique), la courbure du temps seule est suffisante pour dériver la loi de gravité de Newton .
La gravitation newtonienne est une théorie du temps courbe. La relativité générale est une théorie du temps courbe et de l'espace courbe. Étant donné G comme la constante gravitationnelle, M comme la masse d'une étoile newtonienne et des corps en orbite de masse insignifiante à la distance r de l'étoile, l'intervalle d'espace-temps pour la gravitation newtonienne est celui pour lequel seul le coefficient de temps est variable :
Courbure de l'espace
Le coefficient devant décrit la courbure du temps dans la gravitation newtonienne, et cette courbure rend compte complètement de tous les effets gravitationnels newtoniens. Comme prévu, ce facteur de correction est directement proportionnel à et , et à cause du dénominateur, le facteur de correction augmente à mesure que l'on s'approche du corps gravitant, ce qui signifie que le temps est courbé.
Mais la relativité générale est une théorie de l'espace courbe et du temps courbe, donc s'il existe des termes modifiant les composantes spatiales de l'intervalle d'espace-temps présenté ci-dessus, leurs effets ne devraient-ils pas être observés, par exemple, sur les orbites planétaires et satellitaires en raison des facteurs de correction de courbure appliqués aux termes spatiaux ?
La réponse est qu'ils sont vus, mais les effets sont minimes. La raison en est que les vitesses planétaires sont extrêmement faibles par rapport à la vitesse de la lumière, de sorte que pour les planètes et les satellites du système solaire, le terme éclipse les termes spatiaux.
Malgré la minutie des termes spatiaux, les premières indications que quelque chose n'allait pas avec la gravitation newtonienne ont été découvertes il y a plus d'un siècle et demi. En 1859, Urbain Le Verrier , dans une analyse des observations chronométrées disponibles des transits de Mercure sur le disque solaire de 1697 à 1848, rapporta que la physique connue ne pouvait pas expliquer l'orbite de Mercure, à moins qu'il n'existe éventuellement une planète ou une ceinture d'astéroïdes dans le disque solaire. orbite de Mercure. Le périhélie de l'orbite de Mercure présentait un taux de précession excessif par rapport à ce qui pouvait s'expliquer par les remorqueurs des autres planètes. La capacité de détecter et de mesurer avec précision la valeur infime de cette précession anormale (seulement 43 secondes d'arc par siècle tropical ) témoigne de la sophistication de l' astrométrie du XIXe siècle .

Comme le célèbre astronome qui avait découvert plus tôt l'existence de Neptune "au bout de sa plume" en analysant les oscillations de l'orbite d'Uranus, l'annonce de Le Verrier a déclenché une longue période de deux décennies de "Vulcan-mania", en tant que professionnel et amateur les astronomes chassaient pour la nouvelle planète hypothétique. Cette recherche comprenait plusieurs fausses observations de Vulcain. Il a finalement été établi qu'aucune planète ou ceinture d'astéroïdes n'existait.
En 1916, Einstein devait montrer que cette précession anormale de Mercure s'explique par les termes spatiaux de la courbure de l'espace-temps. La courbure dans le terme temporel, étant simplement une expression de la gravitation newtonienne, n'a aucun rôle dans l'explication de cette précession anormale. Le succès de son calcul était une indication puissante pour les pairs d'Einstein que la théorie générale de la relativité pouvait être correcte.
La plus spectaculaire des prédictions d'Einstein était son calcul selon lequel les termes de courbure dans les composantes spatiales de l'intervalle d'espace-temps pouvaient être mesurés dans la courbure de la lumière autour d'un corps massif. La lumière a une pente de ±1 sur un diagramme d'espace-temps. Son déplacement dans l'espace est égal à son déplacement dans le temps. Pour l'expression de champ faible de l'intervalle invariant, Einstein a calculé une courbure de signe exactement égale mais opposée dans ses composantes spatiales.
Dans la gravitation de Newton, le coefficient devant prédit la courbure de la lumière autour d'une étoile. En relativité générale, le coefficient devant prédit un doublement de la flexion totale.
L'histoire de l' expédition de l'éclipse d'Eddington en 1919 et de l'ascension d'Einstein vers la gloire est bien racontée ailleurs.
Sources de courbure de l'espace-temps
Dans la théorie de la gravitation de Newton , la seule source de force gravitationnelle est la masse .
En revanche, la relativité générale identifie plusieurs sources de courbure de l'espace-temps en plus de la masse. Dans les équations du champ d'Einstein , les sources de gravité sont présentées du côté droit du tenseur contrainte-énergie .
La Fig. 5-5 classe les différentes sources de gravité dans le tenseur énergie-contrainte :
- (rouge) : la densité masse-énergie totale, y compris toute contribution à l'énergie potentielle des forces entre les particules, ainsi que l'énergie cinétique des mouvements thermiques aléatoires.
- et (orange) : ce sont des termes de densité de quantité de mouvement. Même s'il n'y a pas de mouvement de masse, l'énergie peut être transmise par conduction thermique et l'énergie conduite portera l'élan.
- sont les débits de la composante i de la quantité de mouvement par unité de surface dans la direction j . Même s'il n'y a pas de mouvement de masse, les mouvements thermiques aléatoires des particules donneront lieu à un flux d'impulsion, de sorte que les termes i = j (vert) représentent la pression isotrope et les termes i ≠ j (bleu) représentent les contraintes de cisaillement.
Une conclusion importante à tirer des équations est que, familièrement parlant, la gravité elle-même crée la gravité . L'énergie a une masse. Même dans la gravité newtonienne, le champ gravitationnel est associé à une énergie, appelée énergie potentielle gravitationnelle . En relativité générale, l'énergie du champ gravitationnel est réinjectée dans la création du champ gravitationnel. Cela rend les équations non linéaires et difficiles à résoudre dans autre chose que les cas de champ faible. La relativité numérique est une branche de la relativité générale utilisant des méthodes numériques pour résoudre et analyser des problèmes, employant souvent des superordinateurs pour étudier les trous noirs , les ondes gravitationnelles , les étoiles à neutrons et d'autres phénomènes dans le régime de champ fort.
Momentum énergétique
En relativité restreinte, la masse-énergie est étroitement liée à la quantité de mouvement . Tout comme l'espace et le temps sont des aspects différents d'une entité plus complète appelée espace-temps, la masse-énergie et la quantité de mouvement ne sont que des aspects différents d'une quantité unifiée à quatre dimensions appelée quatre impulsions . En conséquence, si la masse-énergie est une source de gravité, la quantité de mouvement doit également en être une. L'inclusion de la quantité de mouvement comme source de gravité conduit à la prédiction que des masses en mouvement ou en rotation peuvent générer des champs analogues aux champs magnétiques générés par des charges en mouvement, un phénomène connu sous le nom de gravitomagnétisme .
Il est bien connu que la force du magnétisme peut être déduite en appliquant les règles de la relativité restreinte aux charges en mouvement. (Une démonstration éloquente de cela a été présentée par Feynman dans le volume II, chapitre 13-6 de ses Lectures on Physics , disponible en ligne.) Une logique analogue peut être utilisée pour démontrer l'origine du gravitomagnétisme. Sur la Fig. 5-7a, deux flux parallèles et infiniment longs de particules massives ont des vitesses égales et opposées − v et + v par rapport à une particule test au repos et centrée entre les deux. En raison de la symétrie de la configuration, la force nette sur la particule centrale est nulle. Supposons que les vitesses soient simplement additives. La figure 5-7b montre exactement la même configuration, mais dans le cadre du courant supérieur. La particule d'essai a une vitesse de + v , et le courant de fond a une vitesse de +2 v . Puisque la situation physique n'a pas changé, seulement le cadre dans lequel les choses sont observées, la particule de test ne doit pas être attirée vers l'un ou l'autre des flux. Mais il n'est pas du tout clair que les forces exercées sur la particule test soient égales. (1) Étant donné que le flux inférieur se déplace plus rapidement que le haut, chaque particule dans le flux inférieur a une énergie de masse plus grande qu'une particule dans le haut. (2) En raison de la contraction de Lorentz, il y a plus de particules par unité de longueur dans le courant inférieur que dans le courant supérieur. (3) Une autre contribution à la masse gravitationnelle active du courant de fond provient d'un terme de pression supplémentaire dont, à ce stade, nous n'avons pas suffisamment de connaissances pour discuter. Tous ces effets ensemble exigeraient apparemment que la particule d'essai soit attirée vers le courant de fond.
La particule d'essai n'est pas attirée vers le courant de fond en raison d'une force dépendant de la vitesse qui sert à repousser une particule qui se déplace dans la même direction que le courant de fond. Cet effet gravitationnel dépendant de la vitesse est le gravitomagnétisme.
La matière en mouvement à travers un champ gravitomagnétique est donc soumise à des effets dits de traînée de trame analogues à l'induction électromagnétique . Il a été proposé que de telles forces gravitomagnétiques sous-tendent la génération des jets relativistes (Fig. 5-8) éjectés par certains trous noirs supermassifs en rotation .
Pression et stress
Les grandeurs qui sont directement liées à l'énergie et à la quantité de mouvement devraient également être des sources de gravité, à savoir la pression interne et la contrainte . Pris ensemble, la masse-énergie , l'élan, la pression et le stress servent tous de sources de gravité : collectivement, ils sont ce qui indique à l'espace-temps comment se courber.
La relativité générale prédit que la pression agit comme une source gravitationnelle avec exactement la même force que la densité masse-énergie. L'inclusion de la pression comme source de gravité conduit à des différences dramatiques entre les prédictions de la relativité générale et celles de la gravitation newtonienne. Par exemple, le terme de pression fixe une limite maximale à la masse d'une étoile à neutrons . Plus une étoile à neutrons est massive, plus il faut de pression pour supporter son poids contre la gravité. La pression accrue, cependant, ajoute à la gravité agissant sur la masse de l'étoile. Au-dessus d'une certaine masse déterminée par la limite de Tolman-Oppenheimer-Volkoff , le processus s'emballe et l'étoile à neutrons s'effondre en un trou noir .
Les termes de contrainte deviennent très significatifs lors de l'exécution de calculs tels que des simulations hydrodynamiques de supernovae à effondrement de cœur.
Ces prédictions des rôles de la pression, de la quantité de mouvement et du stress en tant que sources de courbure de l'espace-temps sont élégantes et jouent un rôle important en théorie. En ce qui concerne la pression, l'univers primitif était dominé par le rayonnement, et il est hautement improbable que l'une des données cosmologiques pertinentes (par exemple , les abondances de nucléosynthèse , etc.) puisse être reproduite si la pression ne contribuait pas à la gravité, ou si elle n'avait pas le même force qu'une source de gravité en tant que masse-énergie. De même, la cohérence mathématique des équations du champ d'Einstein serait rompue si les termes de contrainte ne contribuaient pas en tant que source de gravité.
Test expérimental des sources de courbure de l'espace-temps
Définitions : Masse active, passive et inertielle
Bondi distingue différents types de masse possibles : (1) la masse active ( ) est la masse qui agit comme source d'un champ gravitationnel ; (2) la masse passive ( ) est la masse qui réagit à un champ gravitationnel ; (3) la masse d'inertie ( ) est la masse qui réagit à l'accélération.
- est identique à la masse gravitationnelle ( ) dans la discussion du principe d'équivalence .
Dans la théorie newtonienne,
- La troisième loi d'action et de réaction dicte cela et doit être la même.
- D'autre part, si et sont égaux est un résultat empirique.
En relativité générale,
- L'égalité de et est dictée par le principe d'équivalence.
- Il n'y a pas de principe "d'action et de réaction" dictant une relation nécessaire entre et .
La pression comme source gravitationnelle
L'expérience classique pour mesurer la force d'une source gravitationnelle (c'est-à-dire sa masse active) a été menée pour la première fois en 1797 par Henry Cavendish (Fig. 5-9a). Deux boules petites mais denses sont suspendues à un fil fin, formant un équilibre de torsion . L'approche de deux grandes masses d'essai près des billes introduit un couple détectable. Compte tenu des dimensions de l'appareil et de la constante de ressort mesurable du fil de torsion, la constante gravitationnelle G peut être déterminée.
Étudier les effets de pression en comprimant les masses d'essai est sans espoir, car les pressions de laboratoire atteignables sont insignifiantes par rapport à l' énergie de masse d'une bille métallique.
Cependant, les pressions électromagnétiques répulsives résultant de la compression serrée des protons à l'intérieur des noyaux atomiques sont typiquement de l'ordre de 10 28 atm ≈ 10 33 Pa ≈ 10 33 kg·s −2 m −1 . Cela équivaut à environ 1 % de la masse volumique nucléaire d'environ 10 18 kg/m 3 (après prise en compte de c 2 ≈ 9×10 16 m 2 s −2 ).
Si la pression n'agit pas comme une source gravitationnelle, alors le rapport devrait être plus faible pour les noyaux de numéro atomique Z plus élevé , dans lesquels les pressions électrostatiques sont plus élevées. LB Kreuzer (1968) a fait une expérience Cavendish en utilisant une masse de Téflon en suspension dans un mélange des liquides trichloroéthylène et dibromoéthane ayant la même densité de flottabilité que le Téflon (Fig. 5-9b). Le fluor a le numéro atomique Z = 9 , tandis que le brome a Z = 35 . Kreuzer a découvert que le repositionnement de la masse en téflon ne provoquait aucune déviation différentielle de la barre de torsion, établissant ainsi une masse active et une masse passive équivalentes à une précision de 5 × 10 −5 .
Bien que Kreuzer considérait à l'origine cette expérience comme un simple test du rapport de la masse active à la masse passive, Clifford Will (1976) a réinterprété l'expérience comme un test fondamental du couplage des sources aux champs gravitationnels.
En 1986, Bartlett et Van Buren ont noté que la télémétrie laser lunaire avait détecté un décalage de 2 km entre le centre de la figure de la lune et son centre de masse. Cela indique une asymétrie dans la distribution de Fe (abondant dans le noyau de la Lune) et d'Al (abondant dans sa croûte et son manteau). Si la pression ne contribuait pas de la même manière à la courbure de l'espace-temps que la masse-énergie, la lune ne serait pas sur l'orbite prédite par la mécanique classique. Ils ont utilisé leurs mesures pour resserrer les limites de tout écart entre masse active et masse passive à environ 10 −12 .
Gravitomagnétisme
L'existence du gravitomagnétisme a été prouvée par Gravity Probe B (GP-B) , une mission satellitaire lancée le 20 avril 2004. La phase de vol spatial a duré jusqu'à. L'objectif de la mission était de mesurer la courbure de l'espace-temps près de la Terre, avec un accent particulier sur le gravitomagnétisme .
Les premiers résultats ont confirmé l' effet géodésique relativement important (qui est dû à une simple courbure de l'espace-temps, et est également connu sous le nom de précession de Sitter) avec une précision d'environ 1 %. L' effet de traînée de trame beaucoup plus petit (qui est dû au gravitomagnétisme et est également connu sous le nom de précession Lense – Thirring ) était difficile à mesurer en raison d'effets de charge inattendus provoquant une dérive variable dans les gyroscopes. Néanmoins, par, l'effet de traînée de cadre a été confirmé à moins de 15 % du résultat attendu, tandis que l'effet géodésique a été confirmé à mieux que 0,5 %.
Les mesures ultérieures du glissement de cadre par les observations de télémétrie laser des satellites LARES , LAGEOS -1 et LAGEOS-2 se sont améliorées par rapport à la mesure GP-B , avec des résultats (à partir de 2016) démontrant l'effet à moins de 5% de sa valeur théorique, bien qu'il y ait eu un certain désaccord sur l'exactitude de ce résultat.
Un autre effort, l'expérience Gyroscopes en relativité générale (GINGER), cherche à utiliser trois lasers annulaires de 6 m montés à angle droit les uns par rapport aux autres à 1400 m sous la surface de la Terre pour mesurer cet effet.
Sujets techniques
L'espace-temps est-il vraiment courbe ?
Dans les vues conventionnalistes de Poincaré , les critères essentiels selon lesquels on devrait sélectionner une géométrie euclidienne ou non euclidienne seraient l'économie et la simplicité. Un réaliste dirait qu'Einstein a découvert que l'espace-temps n'était pas euclidien. Un conventionnaliste dirait qu'Einstein trouvait simplement plus pratique d'utiliser une géométrie non euclidienne. Le conventionnaliste soutiendrait que l'analyse d'Einstein ne dit rien sur ce qu'est réellement la géométrie de l'espace-temps .
Cela étant dit,
- 1. Est-il possible de représenter la relativité générale en termes d'espace-temps plat ?
- 2. Existe-t-il des situations où une interprétation plate de l'espace-temps de la relativité générale peut être plus pratique que l'interprétation habituelle de l'espace-temps courbe ?
En réponse à la première question, un certain nombre d'auteurs dont Deser, Grishchuk, Rosen, Weinberg, etc. ont fourni diverses formulations de la gravitation en tant que champ dans une variété plate. Ces théories sont diversement appelées « gravité bimétrique », « approche théorique des champs de la relativité générale », etc. Kip Thorne a fourni une revue populaire de ces théories.
Le paradigme de l'espace-temps plat postule que la matière crée un champ gravitationnel qui fait rétrécir les règles lorsqu'elles sont tournées de l'orientation circonférentielle à radiale, et qui provoque la dilatation des taux de tic-tac des horloges. Le paradigme de l'espace-temps plat est pleinement équivalent au paradigme de l'espace-temps courbe en ce sens qu'ils représentent tous les deux les mêmes phénomènes physiques. Cependant, leurs formulations mathématiques sont entièrement différentes. Les physiciens en activité alternent régulièrement entre l'utilisation de techniques d'espace-temps courbes et plates en fonction des exigences du problème. Le paradigme de l'espace-temps plat s'avère particulièrement pratique pour effectuer des calculs approximatifs dans des champs faibles. Par conséquent, les techniques d'espace-temps plat seront utilisées pour résoudre les problèmes d'ondes gravitationnelles, tandis que les techniques d'espace-temps courbe seront utilisées dans l'analyse des trous noirs.
Symétries asymptotique
Le groupe de symétrie de l'espace-temps pour la relativité restreinte est le groupe de Poincaré , qui est un groupe à dix dimensions de trois boosts de Lorentz, trois rotations et quatre translations d'espace-temps. Il est logique de se demander quelles symétries, le cas échéant, pourraient s'appliquer en relativité générale . Un cas traitable pourrait être de considérer les symétries de l'espace-temps telles que vues par des observateurs situés loin de toutes les sources du champ gravitationnel. L'attente naïve de symétries asymptotiquement plates de l'espace-temps pourrait être simplement d'étendre et de reproduire les symétries de l'espace-temps plat de la relativité restreinte, à savoir. , le groupe de Poincaré.
En 1962 , Hermann Bondi , MG van der Burg, AW Metzner et Rainer K. Sachs ont abordé ce problème de symétrie asymptotique afin d'étudier le flux d'énergie à l'infini dû à la propagation des ondes gravitationnelles . Leur première étape consistait à décider de certaines conditions aux limites physiquement sensibles à placer sur le champ gravitationnel à l'infini lumineux pour caractériser ce que cela signifie de dire qu'une métrique est asymptotiquement plate, sans faire d' hypothèses a priori sur la nature du groupe de symétrie asymptotique - pas même l'hypothèse qu'un tel groupe existe. Ensuite, après avoir conçu ce qu'ils considéraient comme les conditions aux limites les plus sensibles, ils ont étudié la nature des transformations de symétrie asymptotique résultantes qui laissent invariante la forme des conditions aux limites appropriées pour des champs gravitationnels asymptotiquement plats. Ce qu'ils ont découvert, c'est que les transformations de symétrie asymptotique forment en fait un groupe et que la structure de ce groupe ne dépend pas du champ gravitationnel particulier qui se trouve être présent. Cela signifie que, comme prévu, on peut séparer la cinématique de l'espace-temps de la dynamique du champ gravitationnel au moins à l'infini spatial. La surprise déroutante en 1962 a été leur découverte d'un riche groupe de dimension infinie (le soi-disant groupe BMS) en tant que groupe de symétrie asymptotique, au lieu du groupe de Poincaré de dimension finie, qui est un sous-groupe du groupe BMS. Non seulement les transformations de Lorentz sont des transformations de symétrie asymptotique, mais il existe également des transformations supplémentaires qui ne sont pas des transformations de Lorentz mais des transformations de symétrie asymptotique. En fait, ils ont trouvé une infinité supplémentaire de générateurs de transformation appelés supertranslations . Ceci implique la conclusion que la Relativité Générale (RG) ne se réduit pas à la relativité restreinte dans le cas des champs faibles à grande distance.
Géométrie riemannienne
| Géométrie |
|---|

|
| Géomètres |
La géométrie riemannienne est la branche de la géométrie différentielle qui étudie les variétés riemanniennes , variétés lisses à métrique riemannienne , c'est-à-dire avec un produit scalaire sur l' espace tangent en chaque point qui varie régulièrement d'un point à l'autre. Cela donne notamment des notions locales d' angle , de longueur de courbes , de surface et de volume . A partir de celles-ci, d'autres grandeurs globales peuvent être dérivées en intégrant les contributions locales.
La géométrie riemannienne est née de la vision de Bernhard Riemann exprimée dans sa leçon inaugurale " Ueber die Hypothesen, welche der Geometrie zu Grunde liegen " ("Sur les hypothèses sur lesquelles la géométrie est basée"). C'est une généralisation très large et abstraite de la différentielle géométrie des surfaces dans R 3 . Le développement de la géométrie riemannienne a abouti à la synthèse de divers résultats concernant la géométrie des surfaces et le comportement des géodésiques sur celles-ci, avec des techniques applicables à l'étude des variétés différentiables de dimensions supérieures. Il a permis la formulation de la théorie générale de la relativité d'Einstein , a eu un impact profond sur la théorie des groupes et la théorie des représentations , ainsi que sur l'analyse , et a stimulé le développement de la topologie algébrique et différentielle .
Collecteurs courbes
Pour des raisons physiques, un continuum d'espace-temps est défini mathématiquement comme une variété lorentzienne quadridimensionnelle, lisse et connexe . Cela signifie que la métrique lisse de Lorentz a signature . La métrique détermine la géométrie de l'espace-temps , ainsi que la détermination desgéodésiquesdes particules et des faisceaux lumineux. A propos de chaque point (événement) sur cette variété,des tableaux de coordonnéessont utilisés pour représenter les observateurs dans des cadres de référence. Habituellement, les coordonnées cartésiennessont utilisées. De plus, pour des raisons de simplicité, les unités de mesure sont généralement choisies de telle sorte que la vitesse de la lumièresoit égale à 1.
Un cadre de référence (observateur) peut être identifié avec l'un de ces tableaux de coordonnées ; un tel observateur peut décrire n'importe quel événement . Un autre cadre de référence peut être identifié par un deuxième tableau de coordonnées autour de . Deux observateurs (un dans chaque référentiel) peuvent décrire le même événement mais obtenir des descriptions différentes.
Habituellement, de nombreux tableaux de coordonnées qui se chevauchent sont nécessaires pour couvrir un collecteur. Étant donné deux cartes de coordonnées, l'une contenant (représentant un observateur) et l'autre contenant (représentant un autre observateur), l'intersection des cartes représente la région de l'espace-temps dans laquelle les deux observateurs peuvent mesurer des quantités physiques et donc comparer les résultats. La relation entre les deux ensembles de mesures est donnée par une transformation de coordonnées non singulière sur cette intersection. L'idée de cartes de coordonnées en tant qu'observateurs locaux pouvant effectuer des mesures dans leur voisinage a également un bon sens physique, car c'est ainsi que l'on collecte réellement des données physiques - localement.
Par exemple, deux observateurs, dont l'un est sur Terre, mais l'autre qui est sur une fusée rapide vers Jupiter, peuvent observer une comète s'écraser sur Jupiter (c'est l'événement ). En général, ils ne seront pas d'accord sur l'emplacement et le moment exacts de cet impact, c'est-à-dire qu'ils auront des quadruplets différents (car ils utilisent des systèmes de coordonnées différents). Bien que leurs descriptions cinématiques diffèrent, les lois dynamiques (physiques), telles que la conservation de la quantité de mouvement et la première loi de la thermodynamique, seront toujours valables. En fait, la théorie de la relativité exige plus que cela dans le sens où elle stipule que ces lois (et toutes les autres lois physiques) doivent prendre la même forme dans tous les systèmes de coordonnées. Cela introduit des tenseurs dans la relativité, par lesquels toutes les quantités physiques sont représentées.
Les géodésiques sont dites temporelles, nulles ou spatiales si le vecteur tangent à un point de la géodésique est de cette nature. Les trajectoires des particules et des faisceaux lumineux dans l'espace-temps sont représentées respectivement par des géodésiques de type temps et nulles (de type lumière).
Caractère privilégié de l'espace-temps 3+1
Il existe deux types de dimensions : spatiale (bidirectionnelle) et temporelle (unidirectionnelle). Soit le nombre de dimensions spatiales N et le nombre de dimensions temporelles T . Que N = 3 et T = 1, en mettant de côté les dimensions compactifiées invoquées par la théorie des cordes et indétectables à ce jour, peut s'expliquer en faisant appel aux conséquences physiques de laisser N différent de 3 et T différent de 1. L'argument est souvent d'un caractère anthropique et peut-être le premier du genre, bien qu'avant que le concept complet n'entre en vogue.
La notion implicite que la dimensionnalité de l'univers est spéciale est d'abord attribuée à Gottfried Wilhelm Leibniz , qui dans le Discours sur la métaphysique a suggéré que le monde est « celui qui est à la fois le plus simple en hypothèses et le plus riche en phénomènes ». Immanuel Kant a soutenu que l'espace tridimensionnel était une conséquence de la loi du carré inverse de la gravitation universelle . Bien que l'argument de Kant soit historiquement important, John D. Barrow a déclaré qu'il "remet la punchline à l'envers: c'est la tridimensionnalité de l'espace qui explique pourquoi nous voyons des lois de force en carré inverse dans la nature, et non l'inverse. " (Barrow 2002 : 204).
En 1920, Paul Ehrenfest a montré que s'il n'y a qu'une seule dimension temporelle et plus de trois dimensions spatiales, l' orbite d'une planète autour de son Soleil ne peut pas rester stable. Il en va de même pour l'orbite d'une étoile autour du centre de sa galaxie . Ehrenfest a également montré que s'il existe un nombre pair de dimensions spatiales, les différentes parties d'une impulsion d' onde se déplaceront à des vitesses différentes. S'il existe des dimensions spatiales, où k est un nombre entier positif, les impulsions des ondes sont déformées. En 1922, Hermann Weyl a montré que la théorie de l'électromagnétisme de Maxwell ne fonctionne qu'avec trois dimensions d'espace et une de temps. Enfin, Tangherlini a montré en 1963 que lorsqu'il y a plus de trois dimensions spatiales, les orbitales d'électrons autour des noyaux ne peuvent pas être stables ; les électrons tomberaient dans le noyau ou se disperseraient.
Max Tegmark développe l'argument précédent de la manière anthropique suivante. Si T diffère de 1, le comportement des systèmes physiques ne peut pas être prédit de manière fiable à partir de la connaissance des équations aux dérivées partielles pertinentes . Dans un tel univers, une vie intelligente capable de manipuler la technologie ne pourrait pas émerger. De plus, si T > 1, Tegmark soutient que les protons et les électrons seraient instables et pourraient se désintégrer en particules ayant une masse supérieure à eux-mêmes. (Ce n'est pas un problème si les particules ont une température suffisamment basse.)
Enfin, si N < 3, la gravitation quelle qu'elle soit devient problématique, et l'univers est probablement trop simple pour contenir des observateurs. Par exemple, lorsque N < 3, les nerfs ne peuvent pas se croiser sans se croiser.
Par conséquent, les arguments anthropiques et autres excluent tous les cas sauf N = 3 et T = 1, qui se trouve décrire le monde qui nous entoure.
En 2019, James Scargill a fait valoir qu'une vie complexe peut être possible avec deux dimensions spatiales. Selon Scargill, une théorie purement scalaire de la gravité peut permettre une force gravitationnelle locale, et les réseaux 2D peuvent être suffisants pour les réseaux de neurones complexes.Voir également
Remarques
Détails supplémentaires
Références
Lectures complémentaires
- Barrow, John D. ; Tipler, Frank J. (1986). Le principe cosmologique anthropique (1ère éd.). Presse universitaire d'Oxford . ISBN 978-0-19-282147-8. RCAC 87028148 .
- George F. Ellis et Ruth M. Williams (1992) Espaces-temps plats et courbes . Université d'Oxford. Presse. ISBN 0-19-851164-7
- Lorentz, HA , Einstein, Albert , Minkowski, Hermann et Weyl, Hermann (1952) Le principe de relativité : une collection de mémoires originaux . Douvres.
- Lucas, John Randolph (1973) Un traité sur le temps et l'espace . Londres : Methuen.
- Penrose, Roger (2004). La route vers la réalité . Oxford : presse universitaire d'Oxford. ISBN 0-679-45443-8.Chpts. 17–18.
- Taylor, EF; Wheeler, John A. (1992). Physique de l'espace-temps, deuxième édition . Archives Internet : WH Freeman. ISBN 0-7167-2327-1.
- Arkani-Hamed, Nima (1er décembre 2017). Le destin de l'espace-temps : pourquoi il doit se dissoudre dans des structures plus fondamentales (discours). La 2 384e réunion de la Société. Washington, DC . Récupéré le 16 juillet 2022 .
Liens externes
-
 Médias liés à l' espace -temps sur Wikimedia Commons
Médias liés à l' espace -temps sur Wikimedia Commons - Albert Einstein sur l'espace-temps 13e édition Encyclopædia Britannica Historique: article d'Albert Einstein de 1926
- Encyclopédie de l'espace-temps et de la gravitation Scholarpedia Articles d'experts
- Stanford Encyclopedia of Philosophy : " Space and Time : Inertial Frames " par Robert DiSalle.








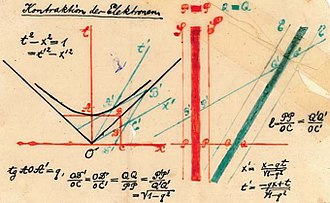








































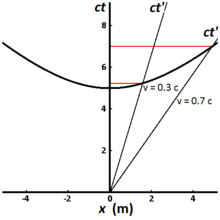

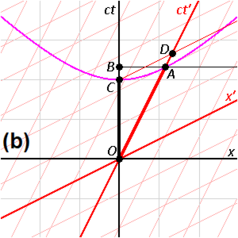

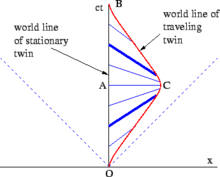




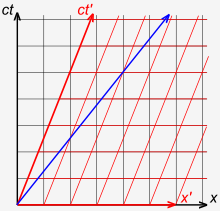





















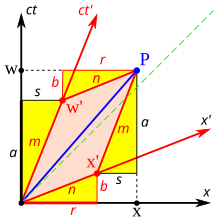




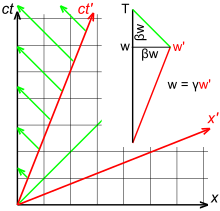



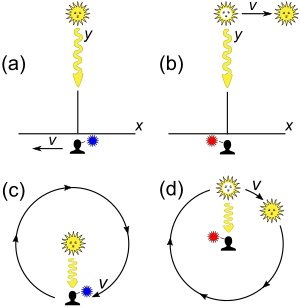






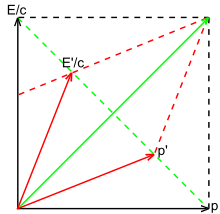













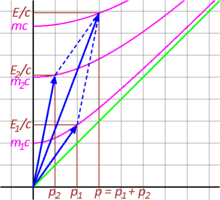











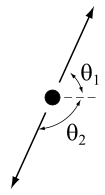







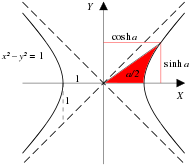


































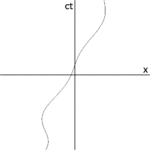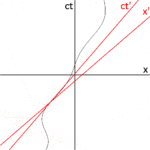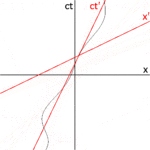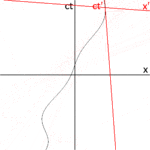











































![{\displaystyle -\,\left(1+{\frac {2GM}{c^{2}r}}\right)\left[(\Delta x)^{2}+(\Delta y)^{2 }+(\Delta z)^{2}\droite]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e004b8eb220d5cc0f0e835a4f9a584ebfdc3ef02)

![{\displaystyle \left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b88b386b994cad15b04251eedd908b3828db4d66)