Harmoniques sphériques - Spherical harmonics

En mathématiques et en sciences physiques , les harmoniques sphériques sont des fonctions spéciales définies à la surface d'une sphère . Ils sont souvent utilisés pour résoudre des équations aux dérivées partielles dans de nombreux domaines scientifiques.

Puisque les harmoniques sphériques forment un ensemble complet de fonctions orthogonales et donc une base orthonormée , chaque fonction définie à la surface d'une sphère peut s'écrire comme une somme de ces harmoniques sphériques. Ceci est similaire aux fonctions périodiques définies sur un cercle qui peuvent être exprimées comme une somme de fonctions circulaires (sinus et cosinus) via des séries de Fourier . Comme les sinus et les cosinus de la série de Fourier, les harmoniques sphériques peuvent être organisées par fréquence angulaire (spatiale) , comme le montrent les rangées de fonctions de l'illustration de droite. De plus, les harmoniques sphériques sont des fonctions de base pour les représentations irréductibles de SO(3) , le groupe des rotations en trois dimensions, et jouent ainsi un rôle central dans la discussion théorique de groupe de SO(3).

Les harmoniques sphériques proviennent de la résolution de l'équation de Laplace dans les domaines sphériques. Les fonctions qui sont des solutions à l'équation de Laplace sont appelées harmoniques. Malgré leur nom, les harmoniques sphériques prennent leur forme la plus simple en coordonnées cartésiennes , où ils peuvent être définis comme des polynômes homogènes de degré en obéissant à l' équation de Laplace. Le rapprochement avec les coordonnées sphériques se fait immédiatement si l'on utilise l'homogénéité pour extraire un facteur de dépendance radiale du polynôme de degré précité ; le facteur restant peut être considéré comme une fonction des coordonnées angulaires sphériques et uniquement, ou de manière équivalente, du vecteur unité d' orientation spécifié par ces angles. Dans ce cadre, ils peuvent être considérés comme la partie angulaire d'un ensemble de solutions à l'équation de Laplace en trois dimensions, et ce point de vue est souvent pris comme une définition alternative. ${\style d'affichage \ell }$${\style d'affichage (x,y,z)}$${\displaystyle r^{\ell }}$${\style d'affichage \ell }$${\displaystyle \theta }$${\displaystyle \varphi }$ ${\displaystyle \mathbf {r} }$

Un ensemble spécifique d'harmoniques sphériques, noté ou , sont connus sous le nom d'harmoniques sphériques de Laplace, car ils ont été introduits pour la première fois par Pierre Simon de Laplace en 1782. Ces fonctions forment un système orthogonal , et sont donc à la base de l'expansion d'une fonction générale sur le sphère comme mentionné ci-dessus. ${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )}$${\displaystyle Y_{\ell }^{m}({\mathbf {r} })}$

Les harmoniques sphériques sont importantes dans de nombreuses applications théoriques et pratiques, notamment la représentation des champs électrostatiques et électromagnétiques multipolaires , les configurations électroniques , les champs gravitationnels , les géoïdes , les champs magnétiques des corps planétaires et des étoiles et le rayonnement de fond cosmique micro-ondes . En infographie 3D , les harmoniques sphériques jouent un rôle dans une grande variété de sujets, notamment l'éclairage indirect ( occlusion ambiante , illumination globale , transfert de radiance précalculé , etc.) et la modélisation de formes 3D.

Histoire

Les harmoniques sphériques ont d'abord été étudiées en relation avec le potentiel newtonien de la loi de la gravitation universelle de Newton en trois dimensions. En 1782, Pierre-Simon de Laplace avait, dans sa Mécanique céleste , déterminé que le potentiel gravitationnel en un point x associé à un ensemble de masses ponctuelles m _i situées aux points x _i était donné par ${\displaystyle \mathbb {R} ^{3}\to \mathbb {R} }$

${\displaystyle V(\mathbf {x} )=\sum _{i}{\frac {m_{i}}{|\mathbf {x} _{i}-\mathbf {x} |}}.}$

Chaque terme de la sommation ci-dessus est un potentiel newtonien individuel pour une masse ponctuelle. Juste avant cette époque, Adrien-Marie Legendre avait étudié l'expansion du potentiel newtonien en puissances de r = | x | et r ₁ = | x ₁ | . Il a découvert que si r ≤ r ₁ alors

${\displaystyle {\frac {1}{|\mathbf {x} _{1}-\mathbf {x} |}}=P_{0}(\cos \gamma ){\frac {1}{r_{1 }}}+P_{1}(\cos \gamma ){\frac {r}{r_{1}^{2}}}+P_{2}(\cos \gamma ){\frac {r^{2 }}{r_{1}^{3}}}+\cdots }$

où γ est l'angle entre les vecteurs x et x ₁ . Les fonctions sont les polynômes de Legendre , et elles peuvent être dérivées comme un cas particulier d'harmoniques sphériques. Par la suite, dans son mémoire 1782, Laplace étudié ces coefficients en utilisant les coordonnées sphériques pour représenter l'angle γ entre x ₁ et x . (Voir Applications des polynômes de Legendre en physique pour une analyse plus détaillée.) ${\displaystyle P_{i}:[-1,1]\to \mathbb {R} }$

En 1867, William Thomson (Lord Kelvin) et Peter Guthrie Tait ont introduit les harmoniques sphériques solides dans leur Traité de philosophie naturelle , et ont également introduit pour la première fois le nom d'« harmoniques sphériques » pour ces fonctions. Les harmoniques solides étaient des solutions polynomiales homogènes de l'équation de Laplace${\displaystyle \mathbb {R} ^{3}\to \mathbb {R} }$

${\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{ \frac {\partiel ^{2}u}{\partiel z^{2}}}=0.}$

En examinant l'équation de Laplace en coordonnées sphériques, Thomson et Tait ont récupéré les harmoniques sphériques de Laplace. (Voir la section ci-dessous, « Représentation polynomiale harmonique ».) Le terme « coefficients de Laplace » a été utilisé par William Whewell pour décrire le système particulier de solutions introduit le long de ces lignes, tandis que d'autres ont réservé cette désignation pour les harmoniques sphériques zonales qui avaient été correctement été présenté par Laplace et Legendre.

Le développement des séries de Fourier au XIXe siècle a rendu possible la solution d'une grande variété de problèmes physiques dans des domaines rectangulaires, tels que la solution de l' équation de la chaleur et de l'équation des ondes . Ceci pourrait être réalisé par l'expansion des fonctions en séries de fonctions trigonométriques . Alors que les fonctions trigonométriques d'une série de Fourier représentent les modes fondamentaux de vibration dans une corde , les harmoniques sphériques représentent les modes fondamentaux de vibration d'une sphère à peu près de la même manière. De nombreux aspects de la théorie des séries de Fourier pourraient être généralisés en prenant des développements en harmoniques sphériques plutôt que des fonctions trigonométriques. De plus, de manière analogue à la façon dont les fonctions trigonométriques peuvent être écrites de manière équivalente sous forme d' exponentielles complexes , les harmoniques sphériques possédaient également une forme équivalente en tant que fonctions à valeurs complexes. C'était une aubaine pour les problèmes possédant une symétrie sphérique , comme ceux de la mécanique céleste initialement étudiés par Laplace et Legendre.

La prévalence des harmoniques sphériques déjà en physique a ouvert la voie à leur importance ultérieure dans la naissance de la mécanique quantique au 20e siècle . Les harmoniques sphériques (à valeur complexe) sont des fonctions propres du carré de l' opérateur de moment angulaire orbital${\displaystyle S^{2}\à \mathbb {C} }$

${\displaystyle -i\hbar \mathbf {r} \times \nabla ,}$

et donc ils représentent les différentes configurations quantifiées des orbitales atomiques .

Harmoniques sphériques de Laplace

L'équation de Laplace impose que le laplacien d'un champ scalaire f soit nul. (Ici le champ scalaire est compris comme complexe, c'est-à-dire qu'il correspond à une fonction (lisse) .) En coordonnées sphériques c'est : ${\displaystyle f:\mathbb {R} ^{3}\to \mathbb {C} }$

${\displaystyle \nabla ^{2}f={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac { \partial f}{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\ sin \theta {\frac {\partial f}{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}f}{\partiel \varphi ^{2}}}=0.}$

Considérons le problème de trouver des solutions de la forme f ( r , θ , φ ) = R ( r ) Y ( θ , φ ) . Par séparation de variables , deux équations différentielles résultent en imposant l'équation de Laplace :

${\displaystyle {\frac {1}{R}}{\frac {d}{dr}}\left(r^{2}{\frac {dR}{dr}}\right)=\lambda ,\qquad {\frac {1}{Y}}{\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial Y}{\partial \theta }}\right)+{\frac {1}{Y}}{\frac {1}{\sin ^{2}\theta }}{\frac {\partial ^{2} Y}{\partial \varphi ^{2}}}=-\lambda .}$

La seconde équation peut être simplifiée dans l'hypothèse où Y a la forme Y ( θ , φ ) = Θ ( θ ) Φ ( φ ) . L'application à nouveau de la séparation des variables à la deuxième équation cède la place à la paire d'équations différentielles

${\displaystyle {\frac {1}{\Phi }}{\frac {d^{2}\Phi }{d\varphi ^{2}}}=-m^{2}}$

${\displaystyle \lambda \sin ^{2}\theta +{\frac {\sin \theta }{\Theta }}{\frac {d}{d\theta }}\left(\sin \theta {\frac {d\Thêta }{d\thêta }}\right)=m^{2}}$

pour un certain nombre m . A priori, m est une constante complexe, mais comme Φ doit être une fonction périodique dont la période divise régulièrement 2 π , m est nécessairement un entier et Φ est une combinaison linéaire des exponentielles complexes e ^{± imφ} . La fonction solution Y ( θ , φ ) est régulière aux pôles de la sphère, où θ = 0, π . Imposer cette régularité dans la solution Θ de la seconde équation aux points limites du domaine est un problème de Sturm-Liouville que les forces du paramètre X pour être de la forme λ = ℓ ( ℓ + 1) pour un entier non négatif avec ℓ | m | ; ceci est également expliqué ci-dessous en termes de moment angulaire orbital . De plus, un changement de variables t = cos θ transforme cette équation en l' équation de Legendre , dont la solution est un multiple du polynôme de Legendre associé P^m
_ℓ(cos θ ) . Enfin, l'équation de R a des solutions de la forme R ( r ) = A r ^ℓ + B r ^{− ℓ − 1} ; nécessitant que la solution soit régulière tout au long de R ³ forces B = 0 .

Ici , la solution a été supposé avoir la forme spéciale Y ( θ , φ ) = Θ ( θ ) Φ ( φ ) . Pour une valeur donnée de ℓ , il y a 2 ℓ + 1 solutions indépendantes de cette forme, un pour chaque nombre entier m avec - ℓ ≤ m ≤ ℓ . Ces solutions angulaires sont un produit de fonctions trigonométriques , représentées ici sous la forme d'une exponentielle complexe , et des polynômes de Legendre associés : ${\displaystyle Y_{\ell }^{m}:S^{2}\to \mathbb {C} }$

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=Ne^{im\varphi }P_{\ell }^{m}(\cos {\theta })}$

qui remplissent

${\displaystyle r^{2}\nabla ^{2}Y_{\ell }^{m}(\theta ,\varphi )=-\ell (\ell +1)Y_{\ell }^{m}( \theta ,\varphi ).}$

Ici , est appelée une fonction harmonique sphérique de degré ℓ et de l' ordre m , est un polynôme de Legendre associé , N est une constante de normalisation, et θ et & phiv représentent colatitude et longitude, respectivement. En particulier, l' colatitude θ , ou angle polaire, varie de 0 au pôle Nord, à tc / 2 à l'équateur, à tc au pôle Sud et la longitude φ , ou azimut , peut prendre toutes les valeurs avec 0 ≤ φ <2 π . Pour un nombre entier fixe ℓ , chaque solution Y ( θ , φ ) , de la valeur propre problème ${\displaystyle Y_{\ell }^{m}:S^{2}\to \mathbb {C} }$${\displaystyle P_{\ell }^{m}:[-1,1]\to \mathbb {R} }$ ${\displaystyle Y:S^{2}\to \mathbb {C} }$

${\displaystyle r^{2}\nabla ^{2}Y=-\ell (\ell +1)Y}$

est une combinaison linéaire de . En effet, pour une telle solution, r ^ℓ Y ( θ , φ ) est l'expression en coordonnées sphériques d'un polynôme homogène qui est harmonique (voir ci - dessous ), et ainsi les dimensions de comptage montre qu'il y a 2 ℓ + 1 tels polynômes linéairement indépendants . ${\displaystyle Y_{\ell }^{m}:S^{2}\to \mathbb {C} }$ ${\displaystyle \mathbb {R} ^{3}\to \mathbb {C} }$

La solution générale de l'équation de Laplace dans une boule centrée à l'origine est une combinaison linéaire des fonctions harmoniques sphériques multipliées par le facteur d'échelle approprié r ^ℓ , ${\displaystyle f:\mathbb {R} ^{3}\to \mathbb {C} }$ ${\style d'affichage \Delta f=0}$

${\displaystyle f(r,\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{\ell }^{ m}r^{\ell }Y_{\ell }^{m}(\theta ,\varphi ),}$

où le sont des constantes et les facteurs r ^ℓ Y _ℓ ^m sont connus comme ( réguliers ) harmoniques solides . Une telle expansion est valable dans la balle${\displaystyle f_{\ell }^{m}\in \mathbb {C} }$ ${\displaystyle \mathbb {R} ^{3}\to \mathbb {C} }$

${\displaystyle r<R={\frac {1}{\limsup _{\ell \to \infty }|f_{\ell }^{m}|^{{1}/{\ell }}}}. }$

Pour , les harmoniques solides avec des puissances négatives de (les harmoniques solides irrégulières ) sont choisies à la place. Dans ce cas, il faut développer la solution des régions connues dans la série de Laurent (environ ), au lieu de la série de Taylor (environ ) utilisée ci-dessus, pour faire correspondre les termes et trouver les coefficients de développement de la série . ${\style d'affichage r>R}$${\style d'affichage r}$ ${\displaystyle \mathbb {R} ^{3}\setminus \{\mathbf {0} \}\to \mathbb {C} }$${\displaystyle r=\infty }$${\style d'affichage r=0}$${\displaystyle f_{\ell }^{m}\in \mathbb {C} }$

Moment angulaire orbital

En mécanique quantique, les harmoniques sphériques de Laplace sont comprises en termes de moment angulaire orbital

${\displaystyle \mathbf {L} =-i\hbar (\mathbf {x} \times \mathbf {\nabla } )=L_{x}\mathbf {i} +L_{y}\mathbf {j} +L_ {z}\mathbf {k} .}$

Le ħ est classique en mécanique quantique; il est commode de travailler dans des unités où ¯h = 1 . Les harmoniques sphériques sont des fonctions propres du carré du moment angulaire orbital

${\displaystyle {\begin{aligned}\mathbf {L} ^{2}&=-r^{2}\nabla ^{2}+\left(r{\frac {\partial }{\partial r}} +1\right)r{\frac {\partial }{\partial r}}\\&=-{\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta } }\sin \theta {\frac {\partial }{\partial \theta }}-{\frac {1}{\sin ^{2}\theta }}{\frac {\partial ^{2}}{\ partiel \varphi ^{2}}}.\end{aligned}}}$

Les harmoniques sphériques de Laplace sont les fonctions propres conjointes du carré du moment angulaire orbital et du générateur de rotations autour de l'axe azimutal :

${\displaystyle {\begin{aligned}L_{z}&=-i\left(x{\frac {\partial }{\partial y}}-y{\frac {\partial }{\partial x}}\ à droite)\\&=-i{\frac {\partial }{\partial \varphi }}.\end{aligned}}}$

Ces opérateurs commutent, et sont des opérateurs auto-adjoints densément définis sur l' espace de Hilbert pondéré des fonctions f carré-intégrable par rapport à la distribution normale comme fonction de poids sur R ³ :

${\displaystyle {\frac {1}{(2\pi )^{3/2}}}\int _{\mathbb {R} ^{3}}|f(x)|^{2}e^{ -|x|^{2}/2}\,dx<\infty .}$

De plus, L ² est un opérateur positif .

Si Y est une fonction propre conjointe de L ² et L _z , alors par définition

${\displaystyle {\begin{aligned}\mathbf {L} ^{2}Y&=\lambda Y\\L_{z}Y&=mY\end{aligned}}}$

pour certains nombres réels m et λ . Ici m doivent en effet être un nombre entier, pour Y doit être périodique à la coordonnée φ avec la période d' un nombre qui divise uniformément 2 π . De plus, depuis

${\displaystyle \mathbf {L} ^{2}=L_{x}^{2}+L_{y}^{2}+L_{z}^{2}}$

et chacun de L _x , L _y , L _z sont autoadjointe, il en résulte que X ≥ m ² .

On note cette sous - espace commun de E _{λ , m} , et définir la montée et la descente des opérateurs par

${\displaystyle {\begin{aligned}L_{+}&=L_{x}+iL_{y}\\L_{-}&=L_{x}-iL_{y}\end{aligned}}}$

Alors L ₊ et L ₋ commutent avec L ² , et l'algèbre de Lie engendrée par L ₊ , L ₋ , L _z est l' algèbre de Lie linéaire spéciale d'ordre 2, , avec des relations de commutation ${\displaystyle {\mathfrak {sl}}_{2}(\mathbb {C} )}$

${\displaystyle [L_{z},L_{+}]=L_{+},\quad [L_{z},L_{-}]=-L_{-},\quad [L_{+},L_{ -}]=2L_{z}.}$

Ainsi L ₊  : E _{λ , m} → E _{λ , m +1} (c'est un "opérateur montant") et L ₋  : E _{λ , m} → E _{λ , m −1} (c'est un "opérateur descendant"). En particulier, L^k
₊ : E _{λ , m} → E _{λ , m + k} doit être nul pour k suffisamment grand, car l'inégalité λ  ≥  m ² doit être vérifiée dans chacun des espaces propres joints non triviaux. Soit Y  ∈  E _{λ , m} une fonction propre jointe non nulle, et soit k le plus petit entier tel que

${\displaystyle L_{+}^{k}Y=0.}$

Puis, depuis

${\displaystyle L_{-}L_{+}=\mathbf {L} ^{2}-L_{z}^{2}-L_{z}}$

il s'ensuit que

${\displaystyle 0=L_{-}L_{+}^{k}Y=(\lambda -(m+k)^{2}-(m+k))Y.}$

Ainsi λ = ℓ ( ℓ + 1) pour l'entier positif ℓ = m + k .

Tout ce qui précède a été élaboré dans la représentation des coordonnées sphériques, mais peut être exprimé de manière plus abstraite dans la base de ket sphérique orthonormée complète . ${\displaystyle \langle \theta ,\phi |lm\rangle =Y_{l}^{m}(\theta ,\phi )}$

Représentation polynomiale harmonique

Les harmoniques sphériques peuvent être exprimées comme la restriction à la sphère unitaire de certaines fonctions polynomiales . Plus précisément, on dit qu'une fonction polynomiale (à valeurs complexes) est homogène de degré si ${\displaystyle \mathbb {R} ^{3}\to \mathbb {C} }$${\displaystyle p:\mathbb {R} ^{3}\to \mathbb {C} }$${\style d'affichage \ell }$

${\displaystyle p(\lambda \mathbf {x} )=\lambda ^{\ell }p(\mathbf {x} )}$

pour tous les nombres réels et tous . On dit que c'est harmonique si ${\displaystyle \lambda \in \mathbb {R} }$${\displaystyle x\in \mathbb {R} ^{3}}$${\style d'affichage p}$

${\style d'affichage \Delta p=0,}$

où est le Laplacien . Puis pour chacun , on définit ${\style d'affichage \Delta }$${\style d'affichage \ell }$

${\displaystyle \mathbf {A} _{\ell }=\left\{{\text{polynômes harmoniques }}\mathbb {R} ^{3}\to \mathbb {C} {\text{ qui sont homogènes de degré }}\ell \right\}.}$

Par exemple, quand , n'est que l'espace tridimensionnel de toutes les fonctions linéaires , car une telle fonction est automatiquement harmonique. Pendant ce temps, lorsque , nous avons un espace à 5 dimensions : ${\displaystyle \ell =1}$${\displaystyle \mathbf {A} _{1}}$${\displaystyle \mathbb {R} ^{3}\to \mathbb {C} }$${\style d'affichage \ell =1}$

${\displaystyle \mathbf {A} _{2}=\operatorname {span} _{\mathbb {C} }(x_{1}x_{2},\,x_{1}x_{3},\,x_ {2}x_{3},\,x_{1}^{2}-x_{2}^{2},\,x_{1}^{2}-x_{3}^{2}).}$

Pour tout , l'espace des harmoniques sphériques de degré n'est que l'espace des restrictions à la sphère des éléments de . Comme suggéré dans l'introduction, cette perspective est vraisemblablement à l'origine du terme « harmonique sphérique » (c'est-à-dire la restriction à la sphère d'une fonction harmonique ). ${\style d'affichage \ell }$${\displaystyle \mathbf {H} _{\ell }}$${\style d'affichage \ell }$${\style d'affichage S^{2}}$${\displaystyle \mathbf {A} _{\ell }}$

Par exemple, pour toute formule ${\displaystyle c\in \mathbb {C} }$

${\displaystyle p(x_{1},x_{2},x_{3})=c(x_{1}+ix_{2})^{\ell }}$

définit un polynôme homogène de degré avec domaine et codomaine , qui se trouve être indépendant de . Ce polynôme est facilement considéré comme harmonique. Si nous écrivons en coordonnées sphériques puis restreignons à , nous obtenons ${\style d'affichage \ell }$${\displaystyle \mathbb {R} ^{3}\to \mathbb {C} }$${\style d'affichage x_{3}}$${\style d'affichage p}$${\displaystyle (r,\theta ,\phi )}$${\style d'affichage r=1}$

${\displaystyle p(\theta ,\phi )=c\sin(\theta )^{\ell }(\cos(\phi )+i\sin(\phi ))^{\ell },}$

qui peut être réécrit comme

${\displaystyle p(\theta ,\phi )=c\left({\sqrt {1-\cos ^{2}(\theta )}}\right)^{\ell }e^{i\ell \phi }.}$

Après avoir utilisé la formule du polynôme de Legendre associé , nous pouvons reconnaître cela comme la formule de l'harmonique sphérique (Voir la section ci-dessous sur les cas particuliers des harmoniques sphériques.) ${\displaystyle P_{\ell }^{\ell }}$${\displaystyle Y_{\ell }^{\ell }(\theta ,\phi ).}$

Conventions

Orthogonalité et normalisation

Plusieurs normalisations différentes sont couramment utilisées pour les fonctions harmoniques sphériques de Laplace . Tout au long de la section, nous utilisons la convention standard que pour (voir polynômes de Legendre associés ) ${\displaystyle S^{2}\à \mathbb {C} }$${\style d'affichage m>0}$

${\displaystyle P_{\ell }^{-m}=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^ {m}}$

qui est la normalisation naturelle donnée par la formule de Rodrigues.

En acoustique , les harmoniques sphériques de Laplace sont généralement définies comme (c'est la convention utilisée dans cet article)

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{\frac {(2\ell +1)}{4\pi }}{\frac {(\ell - m)!}{(\ell +m)!}}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

tandis qu'en mécanique quantique :

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=(-1)^{m}{\sqrt {{\frac {(2\ell +1)}{4\pi }} {\frac {(\ell -m)!}{(\ell +m)!}}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\ varphi }}$

où sont associés des polynômes de Legendre sans la phase Condon-Shortley (pour éviter de compter la phase deux fois). ${\displaystyle P_{\ell }^{m}}$

Dans les deux définitions, les harmoniques sphériques sont orthonormées

${\displaystyle \int _{\theta =0}^{\pi }\int _{\varphi =0}^{2\pi }Y_{\ell }^{m}\,Y_{\ell '}^ {m'}{}^{*}\,d\Omega =\delta _{\ell \ell '}\,\delta _{mm'},}$

où δ _ij est le delta de Kronecker et d Ω = sin( θ ) dφ dθ . Cette normalisation est utilisée en mécanique quantique car elle garantit que la probabilité est normalisée, c'est-à-dire

${\displaystyle \int {|Y_{\ell }^{m}|^{2}d\Omega }=1.}$

Les disciplines de la géodésie et de l'analyse spectrale utilisent

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{(2\ell +1)}{\frac {(\ell -m)!}{(\ell + m)!}}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

qui possèdent une puissance unitaire

${\displaystyle {\frac {1}{4\pi }}\int _{\theta =0}^{\pi }\int _{\varphi =0}^{2\pi }Y_{\ell }^ {m}\,Y_{\ell '}^{m'}{}^{*}d\Omega =\delta _{\ell \ell '}\,\delta _{mm'}.}$

La communauté magnétique , en revanche, utilise des harmoniques semi-normalisées de Schmidt

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {\frac {(\ell -m)!}{(\ell +m)!}}}\,P_{ \ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

qui ont la normalisation

${\displaystyle \int _{\theta =0}^{\pi }\int _{\varphi =0}^{2\pi }Y_{\ell }^{m}\,Y_{\ell '}^ {m'}{}^{*}d\Omega ={\frac {4\pi }{(2\ell +1)}}\delta _{\ell \ell '}\,\delta _{mm' }.}$

En mécanique quantique, cette normalisation est parfois également utilisée et est nommée normalisation de Racah d'après Giulio Racah .

On peut montrer que toutes les fonctions harmoniques sphériques normalisées ci-dessus satisfont

${\displaystyle Y_{\ell }^{m}{}^{*}(\theta ,\varphi )=(-1)^{m}Y_{\ell }^{-m}(\theta ,\varphi ),}$

où l'exposant * désigne une conjugaison complexe. Alternativement, cette équation découle de la relation des fonctions harmoniques sphériques avec la matrice D de Wigner .

Phase de Condon-Shortley

Une source de confusion avec la définition des fonctions harmoniques sphériques concerne un facteur de phase de (−1) ^m , communément appelé phase Condon- Shortley dans la littérature quantique. Dans la communauté de la mécanique quantique, il est courant soit d'inclure ce facteur de phase dans la définition des polynômes de Legendre associés , soit de l'annexer à la définition des fonctions harmoniques sphériques. Il n'est pas nécessaire d'utiliser la phase Condon-Shortley dans la définition des fonctions harmoniques sphériques, mais l'inclure peut simplifier certaines opérations de mécanique quantique, en particulier l'application d' opérateurs d' élévation et d'abaissement . Les communautés géodésique et magnétique n'incluent jamais le facteur de phase Condon-Shortley dans leurs définitions des fonctions harmoniques sphériques ni dans celles des polynômes de Legendre associés.

Forme réelle

Une base réelle d'harmoniques sphériques peut être définie en termes de leurs analogues complexes en définissant ${\displaystyle Y_{\ell m}:S^{2}\to \mathbb {R} }$${\displaystyle Y_{\ell }^{m}:S^{2}\to \mathbb {C} }$

La convention de phase Condon-Shortley est utilisée ici par souci de cohérence. Les équations inverses correspondantes définissant les harmoniques sphériques complexes en termes d'harmoniques sphériques réelles sont ${\displaystyle Y_{\ell }^{m}:S^{2}\to \mathbb {C} }$${\displaystyle Y_{\ell m}:S^{2}\to \mathbb {R} }$

Les vraies harmoniques sphériques sont parfois appelées harmoniques sphériques tessérales . Ces fonctions ont les mêmes propriétés d'orthonormalité que les fonctions complexes ci- dessus. Les harmoniques sphériques réelles avec m  > 0 sont dites de type cosinus, et celles avec m  < 0 de type sinus. La raison de ceci peut être vue en écrivant les fonctions en termes de polynômes de Legendre comme ${\displaystyle Y_{\ell m}:S^{2}\to \mathbb {R} }$${\displaystyle Y_{\ell }^{m}:S^{2}\to \mathbb {C} }$${\displaystyle Y_{\ell m}}$

Les mêmes facteurs sinus et cosinus peuvent également être vus dans la sous-section suivante qui traite de la représentation cartésienne.

Voir ici pour une liste des harmoniques sphériques réelles jusqu'à et y compris , qui peuvent être considérées comme cohérentes avec la sortie des équations ci-dessus. ${\style d'affichage \ell =4}$

Utilisation en chimie quantique

Comme cela est connu des solutions analytiques pour l'atome d'hydrogène, les fonctions propres de la partie angulaire de la fonction d'onde sont des harmoniques sphériques. Cependant, les solutions de l'équation de Schrödinger non relativiste sans termes magnétiques peuvent être rendues réelles. C'est pourquoi les formes réelles sont largement utilisées dans les fonctions de base de la chimie quantique, car les programmes n'ont alors pas besoin d'utiliser l'algèbre complexe. Ici, il est important de noter que les fonctions réelles couvrent le même espace que les fonctions complexes.

Par exemple, comme le montre le tableau des harmoniques sphériques , les fonctions p habituelles ( ) sont complexes et mélangent les directions des axes, mais les versions réelles ne sont essentiellement que x , y et z . ${\displaystyle \ell =1}$

Harmoniques sphériques sous forme cartésienne

Les harmoniques sphériques complexes donnent naissance aux harmoniques solides en s'étendant de à tous en fonction homogène de degré , c'est à dire en fixant ${\displaystyle Y_{\ell }^{m}}$${\style d'affichage S^{2}}$${\displaystyle \mathbb {R} ^{3}}$${\style d'affichage \ell }$

${\displaystyle R_{\ell }^{m}(v):=\|v\|^{\ell }Y_{\ell }^{m}({\frac {v}{\|v\|} })}$

Il s'avère que c'est la base de l'espace des polynômes de degré harmoniques et homogènes . Plus précisément, c'est la (unique jusqu'à la normalisation) base Gelfand-Tsetlin de cette représentation du groupe rotationnel et une formule explicite pour en coordonnées cartésiennes peut être dérivée de ce fait. ${\displaystyle R_{\ell }^{m}}$${\style d'affichage \ell }$${\style d'affichage SO(3)}$${\displaystyle R_{\ell }^{m}}$

La fonction génératrice de Herglotz

Si la convention de mécanique quantique est adoptée pour le , alors ${\displaystyle Y_{\ell }^{m}:S^{2}\to \mathbb {C} }$

${\displaystyle e^{v{\mathbf {a} }\cdot {\mathbf {r} }}=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^ {\ell }{\sqrt {\frac {4\pi }{2\ell +1}}}{\frac {r^{\ell }v^{\ell }{\lambda ^{m}}}{ \sqrt {(\ell +m)!(\ell -m)!}}}Y_{\ell }^{m}(\mathbf {r} /r).}$

Ici, est le vecteur avec les composantes , , et ${\displaystyle \mathbf {r} }$${\style d'affichage (x,y,z)\in \mathbb {R} ^{3}}$${\displaystyle r=|\mathbf {r} |}$

${\displaystyle {\mathbf {a} }={\mathbf {\hat {z}} }-{\frac {\lambda }{2}}\left({\mathbf {\hat {x}} }+i {\mathbf {\hat {y}} }\right)+{\frac {1}{2\lambda }}\left({\mathbf {\hat {x}} }-i{\mathbf {\hat { y}} }\droit)}$

est un vecteur à coefficients complexes. Il suffit de prendre et comme paramètres réels. La propriété essentielle de est qu'il est nul : ${\style d'affichage v}$${\style d'affichage \lambda }$${\displaystyle \mathbf {a} }$

${\displaystyle \mathbf {a} \cdot \mathbf {a} =0.}$

En nommant cette fonction génératrice d'après Herglotz , nous suivons Courant & Hilbert 1962 , §VII.7, qui attribuent sa découverte à des notes inédites de lui.

Essentiellement, toutes les propriétés des harmoniques sphériques peuvent être dérivées de cette fonction génératrice. Un avantage immédiat de cette définition est que si le vecteur est remplacé par l' opérateur vecteur spin de la mécanique quantique , tel que l' opérateur analogue de l' harmonique solide , on obtient une fonction génératrice pour un ensemble normalisé d' opérateurs tenseurs sphériques , : ${\displaystyle \mathbf {r} }$${\displaystyle \mathbf {J} }$${\displaystyle {\mathcal {Y}}_{\ell }^{m}({\mathbf {J} })}$ ${\displaystyle r^{\ell }Y_{\ell }^{m}(\mathbf {r} /r)}$${\displaystyle {\mathcal {Y}}_{\ell }^{m}({\mathbf {J} })}$

${\displaystyle e^{v{\mathbf {a} }\cdot {\mathbf {J} }}=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^ {\ell }{\sqrt {\frac {4\pi }{2\ell +1}}}{\frac {v^{\ell }{\lambda ^{m}}}{\sqrt {(\ell +m)!(\ell -m)!}}}{\mathcal {Y}}_{\ell }^{m}({\mathbf {J} }).}$

Le parallélisme des deux définitions garantit que les 's se transforment sous les rotations (voir ci-dessous) de la même manière que les 's, ce qui garantit à son tour qu'il s'agit d'opérateurs tensoriels sphériques, , avec et , obéissant à toutes les propriétés de tels opérateurs, tels que le théorème de composition de Clebsch-Gordan et le théorème de Wigner-Eckart . Ils sont, de plus, un ensemble standardisé avec une échelle ou une normalisation fixe. ${\displaystyle {\mathcal {Y}}_{\ell }^{m}}$${\displaystyle Y_{\ell }^{m}}$${\displaystyle T_{q}^{(k)}}$${\displaystyle k={\ell }}$${\style d'affichage q=m}$

Forme cartésienne séparée

La définition herglotzienne donne des polynômes qui peuvent, si on le souhaite, être encore factorisés en un polynôme de et un autre de et , comme suit (phase Condon-Shortley) : ${\style d'affichage z}$${\style d'affichage x}$${\style d'affichage y}$

${\displaystyle r^{\ell }\,{\begin{pmatrix}Y_{\ell }^{m}\\Y_{\ell }^{-m}\end{pmatrix}}=\left[{\ frac {2\ell +1}{4\pi }}\right]^{1/2}{\bar {\Pi }}_{\ell }^{m}(z){\begin{pmatrix}\ gauche(-1\droite)^{m}(A_{m}+iB_{m})\\(A_{m}-iB_{m})\end{pmatrix}},\qquad m>0.}$

et pour m = 0 :

${\displaystyle r^{\ell }\,Y_{\ell }^{0}\equiv {\sqrt {\frac {2\ell +1}{4\pi }}}{\bar {\Pi }} _{\ell }^{0}.}$

Ici

${\displaystyle A_{m}(x,y)=\sum _{p=0}^{m}{\binom {m}{p}}x^{p}y^{mp}\cos \left( (mp){\frac {\pi }{2}}\right),}$

${\displaystyle B_{m}(x,y)=\sum _{p=0}^{m}{\binom {m}{p}}x^{p}y^{mp}\sin \left( (mp){\frac {\pi }{2}}\right),}$

et

${\displaystyle {\bar {\Pi }}_{\ell }^{m}(z)=\left[{\frac {(\ell -m)!}{(\ell +m)!}}\ right]^{1/2}\sum _{k=0}^{\left\lfloor (\ell -m)/2\right\rfloor }(-1)^{k}2^{-\ell } {\binom {\ell }{k}}{\binom {2}ell -2k}{\ell }}{\frac {(\ell -2k)!}{(\ell -2k-m)!}} \;r^{2k}\;z^{\ell -2k-m}.}$

Car cela se réduit à ${\style d'affichage m=0}$

${\displaystyle {\bar {\Pi }}_{\ell }^{0}(z)=\sum _{k=0}^{\left\lfloor \ell /2\right\rfloor }(-1 )^{k}2^{-\ell }{\binom {\ell }{k}}{\binom {2\ell -2k}{\ell }}\;r^{2k}\;z^{ \ell -2k}.}$

Le facteur est essentiellement le polynôme de Legendre associé , et les facteurs sont essentiellement . ${\displaystyle {\bar {\Pi }}_{\ell }^{m}(z)}$${\displaystyle P_{\ell }^{m}(\cos \theta )}$${\style d'affichage (A_{m}\pm iB_{m})}$${\displaystyle e^{\pm im\varphi }}$

Exemples

En utilisant les expressions pour , , et listées explicitement ci-dessus, nous obtenons : ${\displaystyle {\bar {\Pi }}_{\ell }^{m}(z)}$${\style d'affichage A_{m}(x,y)}$${\style d'affichage B_{m}(x,y)}$

${\displaystyle Y_{3}^{1}=-{\frac {1}{r^{3}}}\left[{\tfrac {7}{4\pi }}\cdot {\tfrac {3} {16}}\right]^{1/2}\left(5z^{2}-r^{2}\right)\left(x+iy\right)=-\left[{\tfrac {7} {4\pi }}\cdot {\tfrac {3}{16}}\right]^{1/2}\left(5\cos ^{2}\theta -1\right)\left(\sin \ theta e^{i\varphi }\right)}$

${\displaystyle Y_{4}^{-2}={\frac {1}{r^{4}}}\left[{\tfrac {9}{4\pi }}\cdot {\tfrac {5} {32}}\right]^{1/2}\left(7z^{2}-r^{2}\right)\left(x-iy\right)^{2}=\left[{\tfrac {9}{4\pi }}\cdot {\tfrac {5}{32}}\right]^{1/2}\left(7\cos ^{2}\theta -1\right)\left( \sin ^{2}\theta e^{-2i\varphi }\right)}$

On peut vérifier que cela est en accord avec la fonction listée ici et ici .

Formes réelles

En utilisant les équations ci-dessus pour former les harmoniques sphériques réelles, on voit que seuls les termes (cosinus) sont inclus et que seuls les termes (sinus) sont inclus : ${\style d'affichage m>0}$${\style d'affichage A_{m}}$${\style d'affichage m<0}$${\style d'affichage B_{m}}$

${\displaystyle r^{\ell }\,{\begin{pmatrix}Y_{\ell m}\\Y_{\ell -m}\end{pmatrix}}={\sqrt {\frac {2\ell + 1}{2\pi }}}{\bar {\Pi }}_{\ell }^{m}(z){\begin{pmatrix}A_{m}\\B_{m}\end{pmatrix} },\qquad m>0.}$

et pour m = 0 :

${\displaystyle r^{\ell }\,Y_{\ell 0}\equiv {\sqrt {\frac {2\ell +1}{4\pi }}}{\bar {\Pi }}_{\ euh }^{0}.}$

Cas particuliers et valeurs

1. Quand , les harmoniques sphériques se réduisent aux polynômes de Legendre ordinaires :${\style d'affichage m=0}$${\displaystyle Y_{\ell }^{m}:S^{2}\to \mathbb {C} }$
   $${\displaystyle Y_{\ell }^{0}(\theta ,\varphi )={\sqrt {\frac {2\ell +1}{4\pi }}}P_{\ell }(\cos \theta ).}$$

   
2. Quand ,${\displaystyle m=\pm \ell }$
   $${\displaystyle Y_{\ell }^{\pm \ell }(\theta ,\varphi )={\frac {(\mp 1)^{\ell }}{2^{\ell }\ell !}} {\sqrt {\frac {(2\ell +1)!}{4\pi }}}\sin ^{\ell }\theta \,e^{\pm i\ell \varphi },}$$

   
   ou plus simplement en coordonnées cartésiennes,
   $${\displaystyle r^{\ell }Y_{\ell }^{\pm \ell }({\mathbf {r} })={\frac {(\mp 1)^{\ell }}{2^{ \ell }\ell !}}{\sqrt {\frac {(2\ell +1)!}{4\pi }}}(x\pm iy)^{\ell }.}$$

   
3. Au pôle nord, où , et n'est pas défini, toutes les harmoniques sphériques à l'exception de celles qui disparaissent :${\displaystyle \theta =0}$${\displaystyle \varphi }$${\style d'affichage m=0}$
   $${\displaystyle Y_{\ell }^{m}(0,\varphi )=Y_{\ell }^{m}({\mathbf {z} })={\sqrt {\frac {2\ell +1 }{4\pi }}}\delta _{m0}.}$$

   

Propriétés de symétrie

Les harmoniques sphériques ont des propriétés profondes et conséquentes sous les opérations d'inversion spatiale (parité) et de rotation.

Parité

Les harmoniques sphériques ont une parité définie. C'est-à-dire qu'ils sont soit pairs soit impairs par rapport à l'inversion de l'origine. L'inversion est représentée par l'opérateur . Ensuite, comme on peut le voir de plusieurs manières (peut-être plus simplement à partir de la fonction génératrice de Herglotz), étant un vecteur unitaire, ${\displaystyle P\Psi (\mathbf {r} )=\Psi (-\mathbf {r} )}$${\displaystyle \mathbf {r} }$

${\displaystyle Y_{\ell }^{m}(-\mathbf {r} )=(-1)^{\ell }Y_{\ell }^{m}(\mathbf {r} ).}$

En termes d'angles sphériques, la parité transforme un point de coordonnées en . L'énoncé de la parité des harmoniques sphériques est alors ${\displaystyle \{\theta ,\phi \}}$${\displaystyle \{\pi -\theta ,\pi +\phi \}}$

${\displaystyle Y_{\ell }^{m}(\theta ,\phi )\rightarrow Y_{\ell }^{m}(\pi -\theta ,\pi +\phi )=(-1)^{ \ell }Y_{\ell }^{m}(\theta ,\phi )}$

(Ceci peut être vu comme suit : Les polynômes de Legendre associés donnent (−1) ^{ℓ + m} et à partir de la fonction exponentielle on a (−1) ^m , donnant ensemble pour les harmoniques sphériques une parité de (−1) ^ℓ .)

La parité continue d'attente pour les harmoniques sphériques réelles, et pour les harmoniques sphériques dans des dimensions supérieures à : appliquer une symétrie centrale à une harmonique sphérique de degré ℓ change le signe d'un facteur (-1) ^ℓ .

Rotations

Considérons une rotation autour de l'origine qui envoie le vecteur unitaire à . Sous cette opération, une harmonique sphérique de degré et d'ordre se transforme en une combinaison linéaire d'harmoniques sphériques de même degré. C'est-à-dire, ${\displaystyle {\mathcal {R}}}$${\displaystyle \mathbf {r} }$${\displaystyle \mathbf {r} '}$${\style d'affichage \ell }$${\style d'affichage m}$

${\displaystyle Y_{\ell }^{m}({\mathbf {r} }')=\sum _{m'=-\ell }^{\ell }A_{mm'}Y_{\ell }^ {m'}({\mathbf {r} }),}$

où est une matrice d'ordre qui dépend de la rotation . Cependant, ce n'est pas la manière standard d'exprimer cette propriété. De la manière habituelle, on écrit, ${\style d'affichage A_{mm'}}$${\style d'affichage (2\ell +1)}$${\displaystyle {\mathcal {R}}}$

${\displaystyle Y_{\ell }^{m}({\mathbf {r} }')=\sum _{m'=-\ell }^{\ell }[D_{mm'}^{(\ell )}({\mathcal {R}})]^{*}Y_{\ell }^{m'}({\mathbf {r} }),}$

où est le conjugué complexe d'un élément de la matrice D de Wigner . En particulier quand est une rotation de l'azimut nous obtenons l'identité, ${\displaystyle D_{mm'}^{(\ell )}({\mathcal {R}})^{*}}$${\displaystyle \mathbf {r} '}$${\displaystyle \phi _{0}}$

${\displaystyle Y_{\ell }^{m}({\mathbf {r} }')=Y_{\ell }^{m}({\mathbf {r} })e^{im\phi _{0 }}.}$

Le comportement rotationnel des harmoniques sphériques est peut-être leur caractéristique par excellence du point de vue de la théorie des groupes. Les 's de degré fournissent un ensemble de fonctions de base pour la représentation irréductible du groupe SO(3) de dimension . De nombreux faits sur les harmoniques sphériques (comme le théorème d'addition) qui sont prouvés laborieusement en utilisant les méthodes d'analyse acquièrent des preuves plus simples et une signification plus profonde en utilisant les méthodes de symétrie. ${\displaystyle Y_{\ell }^{m}}$${\style d'affichage \ell }$${\style d'affichage (2\ell +1)}$

Expansion des harmoniques sphériques

Les harmoniques sphériques de Laplace forment un ensemble complet de fonctions orthonormées et forment ainsi une base orthonormée de l' espace de Hilbert des fonctions carrées intégrables . Sur la sphère unité , toute fonction carrée intégrable peut ainsi être développée comme une combinaison linéaire de celles-ci : ${\displaystyle Y_{\ell }^{m}:S^{2}\to \mathbb {C} }$ ${\displaystyle L_{\mathbb {C} }^{2}(S^{2})}$${\style d'affichage S^{2}}$${\displaystyle f:S^{2}\to \mathbb {C} }$

${\displaystyle f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{\ell }^{m} \,Y_{\ell }^{m}(\theta ,\varphi ).}$

Cette expansion tient dans le sens de la convergence quadratique moyenne — convergence dans L ² de la sphère — c'est-à-dire que

${\displaystyle \lim _{N\to \infty }\int _{0}^{2\pi }\int _{0}^{\pi }\left|f(\theta ,\varphi )-\sum _{\ell =0}^{N}\sum _{m=-\ell }^{\ell }f_{\ell }^{m}Y_{\ell }^{m}(\theta ,\varphi )\right|^{2}\sin \theta \,d\theta \,d\varphi =0.}$

Les coefficients de dilatation sont les analogues des coefficients de Fourier et peuvent être obtenus en multipliant l'équation ci-dessus par le conjugué complexe d'une harmonique sphérique, intégrant sur l'angle solide et utilisant les relations d'orthogonalité ci-dessus. Ceci est rigoureusement justifié par la théorie de base de l'espace de Hilbert. Pour le cas des harmoniques orthonormalisées, cela donne :

${\displaystyle f_{\ell }^{m}=\int _{\Omega }f(\theta ,\varphi )\,Y_{\ell }^{m*}(\theta ,\varphi )\,d \Omega =\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }\,d\theta \,\sin \theta f(\theta ,\varphi )Y_{ \ell }^{m*}(\theta ,\varphi ).}$

Si les coefficients décroissent en ℓ suffisamment rapidement — par exemple, de façon exponentielle — alors la série converge également uniformément vers f .

Une fonction carrée intégrable peut également être étendue en termes d'harmoniques réelles ci-dessus sous forme de somme ${\displaystyle f:S^{2}\to \mathbb {R} }$${\displaystyle Y_{\ell m}:S^{2}\to \mathbb {R} }$

${\displaystyle f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{\ell m}\,Y_ {\ell m}(\theta ,\varphi ).}$

La convergence de la série tient encore dans le même sens, à savoir que les harmoniques sphériques réelles forment un ensemble complet de fonctions orthonormées et forment ainsi une base orthonormée de l' espace de Hilbert des fonctions carrées intégrables . L'avantage de l'expansion en termes de fonctions harmoniques réelles est que pour les fonctions réelles, les coefficients d'expansion sont garantis réels, alors que leurs coefficients dans leur expansion en termes de (en les considérant comme des fonctions ) n'ont pas cette propriété. ${\displaystyle Y_{\ell m}:S^{2}\to \mathbb {R} }$ ${\displaystyle L_{\mathbb {R} }^{2}(S^{2})}$${\displaystyle Y_{\ell m}}$${\displaystyle f:S^{2}\to \mathbb {R} }$${\displaystyle f_{\ell m}}$${\displaystyle f_{\ell }^{m}}$${\displaystyle Y_{\ell }^{m}}$${\displaystyle f:S^{2}\to \mathbb {C} \supset \mathbb {R} }$

Tenseurs harmoniques

Formule

En règle générale, les fonctions harmoniques sont utiles en physique théorique pour considérer les champs dans le champ lointain lorsque la distance des charges est beaucoup plus grande que la taille de leur emplacement. Dans ce cas, le rayon R est constante et les coordonnées ( θ , φ ) sont commodes à utiliser. La physique théorique considère de nombreux problèmes lorsqu'une solution de l'équation de Laplace est nécessaire en fonction des coordonnées artésiennes. En même temps, il est important d'obtenir une forme invariante des solutions par rapport à la rotation de l'espace ou, de manière générale, par rapport aux transformations de groupe. Les solutions tensorielles les plus simples – potentiels dipolaires, quadripolaires et octupôles – sont des concepts fondamentaux de la physique générale :

${\displaystyle {\begin{aligned}T_{i}^{(1)}=x_{i},\\T_{ik}^{(2)}=3x{_{i}}x{_{k }}-\delta _{ik}r^{2},\\T_{ikn}^{(3)}=15x{_{i}}x{_{k}}x{_{n}}- 3\delta _{ik}{r^{2}}x{_{n}}-3\delta _{kn}{r^{2}}x{_{i}}-3\delta _{ni }{r^{2}}x{_{k}}.\end{aligned}}}$

Il est facile de vérifier qu'il s'agit des fonctions harmoniques. L'ensemble total des tenseurs est défini par la série de Taylor d'un potentiel de champ de charge ponctuelle pour : ${\style d'affichage r_{0}<r}$

${\displaystyle {\frac {1}{\left|{\boldsymbol {rr}}{_{0}}\right|}}=\sum _{l}(-1)^{l}{\frac { {({\boldsymbol {r_{0}}}\nabla )}^{l}}{l!}}{\frac {1}{r}}=\sum _{l}{\frac {x_{0i }\ldots x_{0k}}{l!\,r^{2l+1}}}T_{i\ldots k}^{(l)}({\boldsymbol {r}})=\sum _{l }{\frac {\left[\otimes {\boldsymbol {{r_{0}}^{l}T^{(l)}}}\right]}{l!\,r^{2l+1}} },}$

où le tenseur est désigné par le symbole et la contraction des tenseurs est entre parenthèses [...]. Par conséquent, le tenseur est défini par la -ième dérivée du tenseur : ${\displaystyle x_{0i}\ldots x_{0k}}$${\displaystyle \otimes {\boldsymbol {r_{0}}}^{l}}$${\displaystyle {\boldsymbol {T}}^{(l)}}$${\style d'affichage l}$

${\displaystyle {\frac {\boldsymbol {T^{(l)}}}{r^{(2l+1)}}}=(-\otimes {\boldsymbol {\nabla }})^{l}{ \frac {1}{r}}}$

James Clerk Maxwell a naturellement utilisé des considérations similaires sans tenseurs. EW Hobson a également analysé la méthode de Maxwell. On peut voir à partir de l'équation les propriétés suivantes qui répètent principalement celles des fonctions solides et sphériques.

• Le tenseur est le polynôme harmonique c'est-à-dire .${\displaystyle \Delta {\boldsymbol {T}}^{(l)}=0}$
• La trace sur chaque paire d'indices est nulle jusqu'à .${\textstyle \Delta {\frac {1}{r}}=0}$
• Le tenseur est un polynôme homogène de degré, c'est-à-dire que le degré sommé des variables x, y, z de chaque élément est égal à .${\style d'affichage l}$${\style d'affichage l}$
• Le tenseur a une forme invariante sous des rotations de variables x,y,z c'est-à-dire de vecteur .${\displaystyle \mathbf {r} }$
• L'ensemble des potentiels est complet.${\displaystyle \mathbf {T} ^{(l)}}$
• La contraction d' avec un tenseur est proportionnelle à la contraction de deux potentiels harmoniques :${\displaystyle \mathbf {T} ^{(l)}(\mathbf {r} )}$${\displaystyle \otimes {\boldsymbol {\rho }}^{l}}$
  $${\displaystyle \left[\mathbf {T} ^{(l)}(\mathbf {r} )\otimes {\boldsymbol {\rho }}^{l}\right]={\frac {1}{( 2l-1)!!}}\gauche[\mathbf {T} ^{(l)}(\mathbf {r} )\mathbf {T} ^{(l)}({\boldsymbol {\rho }}) \droit]}$$

  

La formule d'un tenseur invariant harmonique a été trouvée dans le papier. Une description détaillée est donnée dans la monographie. Les tenseurs harmoniques 4-D sont importants dans la symétrie de Fock trouvée dans le problème de Coulomb quantique. La formule contient des produits de tenseurs et de symboles de Kronecker : ${\displaystyle x_{i}\ldots x_{k}=\mathbf {\otimes } r^{m}}$ ${\displaystyle \delta _{ik}}$

${\displaystyle \mathbf {T} ^{(l)}=(2l-1)!!\ \mathbf {(} \otimes r^{l})-(2l-3)!!\ r^{2} \left\langle \otimes \mathbf {r} ^{(l-2)}\otimes {\mathsf {\boldsymbol {\delta }}}^{1}\right\rangle +(2l-5)!!\ r^{4}\left\langle \otimes \mathbf {r} ^{(l-4)}\otimes {\mathsf {\boldsymbol {\delta }}}^{2}\right\rangle -\cdots }$

Le nombre de symboles Kronecker est augmenté de deux dans le produit de chaque élément suivant lorsque la plage de tenseurs est réduite de deux en conséquence. L'opération symétrise un tenseur en additionnant toutes les permutations indépendantes d'indices. En particulier, chacun n'a pas besoin d'être transformé en et les tenseurs ne deviennent pas . ${\displaystyle x_{i}\dots x_{k}}$${\displaystyle \left\langle \cdot \right\rangle }$${\displaystyle \delta _{ik}}$${\displaystyle \delta _{ki}}$${\style d'affichage x_{i}x_{k}}$${\style d'affichage x_{k}x_{i}}$

Ces tenseurs sont commodes à substituer dans l'équation de Laplace :

${\displaystyle \Delta \left\langle \otimes \mathbf {r} ^{(l-2k)}\otimes {\mathsf {\boldsymbol {\delta }}}^{k}\right\rangle =2\left \langle \otimes \mathbf {r} ^{(l-2k-2)}\otimes {\mathsf {\boldsymbol {\delta }}}^{(k+2)}\right\rangle ,\quad (\ mathbf {r} \mathbf {\nabla } )\left\langle \otimes \mathbf {r} ^{(l-2k)}\otimes {\mathsf {\boldsymbol {\delta }}}^{(k)} \right\rangle =l\left\langle \otimes \mathbf {r} ^{(l-2k)}\otimes {\mathsf {\boldsymbol {\delta }}}^{(k)}\right\rangle . }$

La dernière relation est la formule d'Euler pour les polynômes homogènes . L'opérateur de Laplace n'affecte pas la symétrie d'indice des tenseurs. Les deux relations permettent de substituer un tenseur dans l'équation de Laplace pour vérifier directement que le tenseur est une fonction harmonique : ${\style d'affichage \Delta }$

${\displaystyle \Delta \mathbf {T} ^{(l)}=0.}$

Des instants simplifiés

La dernière propriété est importante pour la physique théorique pour la raison suivante. Le potentiel des charges en dehors de leur emplacement est intégral pour être égal à la somme des potentiels multipolaires :

${\displaystyle \iiint {\frac {f({\boldsymbol {r}})}{\left||\mathbf {rr} {_{0}}\right|}}\,dx\,dy\,dz =\sum _{l}\iiint f(\mathbf {r} )\left[\mathbf {T} ^{(l)}(\mathbf {r} )dx\,dy\,dz{\frac {\ mathbf {T} ^{(l)}(\mathbf {r} _{0})}{(2l-1)!!\,l!\,r_{0}^{(2l+1)}}} \droit],}$

où est la densité de charge. La convolution est appliquée aux tenseurs dans la formule naturellement. Les intégrales de la somme sont appelées en physique moments multipolaires . Trois d'entre elles sont utilisées activement tandis que d'autres s'appliquent moins souvent car leur structure (ou celle des fonctions sphériques) est plus compliquée. Néanmoins, la dernière propriété permet de simplifier les calculs en physique théorique en utilisant des intégrales avec le tenseur au lieu du tenseur harmonique . Par conséquent, les moments simplifiés donnent le même résultat et il n'est pas nécessaire de restreindre les calculs pour les potentiels dipolaires, quadripolaires et octupôles uniquement. C'est l'avantage du point de vue tenseur et pas le seul. ${\displaystyle {f}(\mathbf {r} )}$${\displaystyle {\boldsymbol {\otimes }}r^{l}}$${\displaystyle \mathbf {T} ^{(l)}}$

L'opérateur d'échelle d'Efimov

Les fonctions sphériques ont quelques formules récurrentes. En mécanique quantique, les formules récurrentes jouent un rôle lorsqu'elles relient des fonctions d' états quantiques au moyen d'un opérateur en échelle . La propriété est due au groupe de symétrie du système considéré. L'opérateur d'échelle vectorielle pour les états harmoniques invariants trouvés dans le papier et détaillés dans. ${\style d'affichage \psi -}$

À cette fin, la transformation de l' espace est appliquée qui conserve la forme de l'équation de Laplace :${\displaystyle {\boldsymbol {\rho }}}$

${\displaystyle {\boldsymbol {\rho }}={\frac {\ \mathbf {r} }{r^{2}}}.}$

L'opérateur s'appliquant au potentiel tenseur harmonique dans l' espace va dans l'opérateur échelle d'Efimov agissant sur le tenseur transformé dans l' espace : ${\displaystyle {\boldsymbol {\nabla }}}$${\displaystyle {\boldsymbol {\rho }}}$${\displaystyle \mathbf {r} }$

${\displaystyle {\hat {\mathbf {D} }}=(2{\hat {l}}-1)\mathbf {r} -r^{2}{\boldsymbol {\nabla }},}$

où est l'opérateur du module du moment cinétique : ${\displaystyle {\hat {l}}}$

${\displaystyle {\hat {l}}=({\boldsymbol {\nabla }}\mathbf {r} ).}$

L'opérateur multiplie le tenseur harmonique par son degré c'est-à-dire par si pour rappeler selon la fonction sphérique pour les nombres quantiques , . Pour vérifier l'action de l'opérateur d'échelle , on peut l'appliquer aux tenseurs dipolaires et quadripolaires : ${\displaystyle {\hat {l}}}$${\style d'affichage l}$ ${\style d'affichage l}$${\style d'affichage m}$${\displaystyle \mathbf {\hat {D}} }$

${\displaystyle \mathbf {\hat {D}} _{i}x_{k}=3x_{i}x_{k}-\delta _{ik},}$

${\displaystyle \mathbf {\hat {D}} _{i}x_{k}x_{n}=15x_{i}x_{k}x_{n}-3\delta _{ik}x_{n}- 3\delta _{kn}x_{i}-3\delta _{ni}x_{k},}$

En appliquant successivement à nous obtenons la forme générale des tenseurs harmoniques invariants : ${\displaystyle \mathbf {\hat {D}} }$${\displaystyle \mathbf {1} }$

${\displaystyle \mathbf {T} ^{(l)}=(\otimes \mathbf {\hat {D}} )^{l}\mathbf {1} .}$

L'opérateur analogue à l' opérateur d'échelle d' oscillateur . Pour tracer une relation avec un opérateur quantique il est utile de le multiplier par pour aller dans l'espace inversé : ${\displaystyle \mathbf {\hat {D}} }$ ${\displaystyle i\hbar }$

${\displaystyle {\boldsymbol {\rho }}={\frac {\mathbf {r} }{r^{2}}}.}$

En conséquence, l'opérateur entre dans l'opérateur de quantité de mouvement dans l' espace : ${\displaystyle {\boldsymbol {\rho }}}$

${\displaystyle \mathbf {\hat {D}} \Rightarrow \mathbf {\hat {p}} .}$

Il est utile d'appliquer les propriétés suivantes de . ${\displaystyle \mathbf {\hat {D}} }$

• Le commutateur des opérateurs de coordonnées est zéro :
  $${\displaystyle {\hat {D}}_{i}{\hat {D}}_{k}-{\hat {D}}_{k}{\hat {D}}_{i}=0 .}$$

  

La propriété est tout à fait pratique pour les calculs.

• L'opérateur scalaire produit est nul dans l'espace des fonctions harmoniques :
  $${\displaystyle {\hat {D}}_{i}{\hat {D}}_{i}={\hat {\mathbf {D} }}{\hat {\mathbf {D} }}=r ^{4}\Delta .}$$

  

La propriété donne une trace nulle du tenseur harmonique sur chacun des deux indices. ${\displaystyle \mathbf {T} ^{l}}$

L'opérateur en échelle est analogue à celui du problème de l' oscillateur quantique . Il génère des états de Glauber qui sont créés dans la théorie quantique des champs de rayonnement électromagnétique. Il a été montré plus tard comme résultat théorique que les états cohérents sont intrinsèques pour tout système quantique avec une symétrie de groupe pour inclure le groupe rotationnel.

Forme invariante des harmoniques sphériques

Les harmoniques sphériques s'accordent avec le système de coordonnées. Soit les vecteurs unitaires le long des axes X, Y, Z. Notons les vecteurs unitaires suivants comme et : ${\displaystyle \mathbf {n} _{x},\mathbf {n} _{y},\mathbf {n} _{z}}$${\displaystyle \mathbf {n} _{+}}$${\displaystyle \ \mathbf {n} _{-}}$

${\displaystyle \mathbf {n} _{\pm }={\frac {(\mathbf {n} _{x}\pm i\mathbf {n} _{y})}{\sqrt {2}}} .}$

En utilisant les vecteurs, les harmoniques solides sont égales à :

${\displaystyle r^{l}Y_{(l\pm m)}=C_{l,m}(\mathbf {n} _{z}\mathbf {\hat {D)}} ^{(lm)} (\mathbf {n} _{\pm }\mathbf {\hat {D)}} ^{m}\mathbf {1} =C_{l,m}\left[\mathbf {M} ^{(l) }\otimes \mathbf {n_{z}} ^{(lm)}\otimes \mathbf {n_{\pm }} ^{m}\right]}$

où est la constante : ${\style d'affichage C_{l,m}}$

${\displaystyle C_{l,m}={\frac {2^{m\setminus 2}{\sqrt {2l+1}}}{\sqrt {(l+m)!(lm)!}}}}$

Le moment angulaire est défini par le groupe de rotation. La quantité de mouvement mécanique est liée au groupe de translation. L'opérateur d'échelle est la cartographie de la quantité de mouvement lors de l'inversion 1/ r de l'espace 3-d. C'est l'opérateur de levage . L'opérateur d'abaissement ici est le gradient naturellement avec une contraction partielle sur les indices de paire pour en laisser les autres : ${\displaystyle \mathbf {\hat {L}} }$${\displaystyle \mathbf {\hat {p}} }$${\style d'affichage i}$

${\displaystyle \left[\partial x_{i}\mathbf {T} _{i}^{(l-1)}\right]=(2l+1)l\,\mathbf {T} ^{(l -1)}}$

Analyse de spectre

Spectre de puissance dans le traitement du signal

La puissance totale d'une fonction f est définie dans la littérature sur le traitement du signal comme l'intégrale de la fonction au carré, divisée par l'aire de son domaine. En utilisant les propriétés d' orthonormalité des fonctions harmoniques sphériques de puissance unitaire réelle, il est simple de vérifier que la puissance totale d'une fonction définie sur la sphère unitaire est liée à ses coefficients spectraux par une généralisation du théorème de Parseval (ici, le théorème est énoncé pour les harmoniques semi-normalisées de Schmidt, la relation est légèrement différente pour les harmoniques orthonormées) :

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }|f(\Omega )|^{2}\,d\Omega =\sum _{\ell =0} ^{\infty }S_{f\!f}(\ell ),}$

où

${\displaystyle S_{f\!f}(\ell )={\frac {1}{2\ell +1}}\sum _{m=-\ell }^{\ell }|f_{\ell m }|^{2}}$

est défini comme le spectre de puissance angulaire (pour les harmoniques semi-normalisées de Schmidt). De la même manière, on peut définir le pouvoir croisé de deux fonctions comme

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )\,g^{\ast }(\Omega )\,d\Omega =\sum _ {\ell =0}^{\infty }S_{fg}(\ell ),}$

où

${\displaystyle S_{fg}(\ell )={\frac {1}{2\ell +1}}\sum _{m=-\ell }^{\ell }f_{\ell m}g_{\ ell m}^{\as }}$

est défini comme le spectre de puissance croisée. Si les fonctions f et g ont une moyenne nulle (les coefficients spectraux f ₀₀ et g ₀₀ sont nuls), puis S _ff ( ℓ ) et S _fg ( ℓ ) représentent les contributions à la variance et covariance de la fonction pour le degré ℓ , respectivement. Il est courant que le spectre de puissance (croisée) soit bien approximé par une loi de puissance de la forme

${\displaystyle S_{f\!f}(\ell )=C\,\ell ^{\beta }.}$

Lorsque β  = 0, le spectre est tel que chaque degré « blanc » possède une puissance égale. Lorsque β  <0, le spectre est appelé « rouge » car il n'y a plus de puissance aux faibles degrés de longueurs d' onde longues que des degrés plus élevés. Enfin, lorsque β  > 0, le spectre est appelé « bleu ». La condition de l'ordre de croissance de S _ff ( ℓ ) est en relation avec l'ordre de différentiabilité de f dans la section suivante.

Propriétés de différentiabilité

On peut aussi comprendre les propriétés de différentiabilité de la fonction d'origine f en termes d' asymptotique de S _ff ( ℓ ). En particulier, si S _ff ( ℓ ) se dégrade plus rapidement que toute fonction rationnelle de ℓ comme ℓ  → ∞, alors f est infiniment différentiables . Si, en outre, S _ff ( ℓ ) diminue de manière exponentielle, alors f est en réalité analytique réelle sur la sphère.

La technique générale consiste à utiliser la théorie des espaces de Sobolev . Des déclarations relatives à la croissance de la S _ff ( ℓ ) à différentiabilité sont alors similaires à des résultats analogues sur la croissance des coefficients de séries de Fourier . Plus précisément, si

${\displaystyle \sum _{\ell =0}^{\infty }(1+\ell ^{2})^{s}S_{ff}(\ell )<\infty ,}$

alors f est dans l'espace de Sobolev H ^s ( S ² ). En particulier, le théorème de plongement de Sobolev implique que f est infiniment dérivable à condition que

${\displaystyle S_{ff}(\ell )=O(\ell ^{-s})\quad {\rm {{as\ }\ell \to \infty }}}$

pour tous les s .

Propriétés algébriques

Théorème d'addition

Un résultat mathématique d'un intérêt et d'une utilisation considérables s'appelle le théorème d'addition pour les harmoniques sphériques. Étant donnés deux vecteurs r et r' , de coordonnées sphériques et , respectivement, l'angle entre eux est donné par la relation ${\displaystyle (r,\theta ,\varphi )}$${\displaystyle (r',\theta ',\varphi ')}$${\style d'affichage \gamma }$

${\displaystyle \cos \gamma =\cos \theta '\cos \theta +\sin \theta \sin \theta '\cos(\varphi -\varphi ')}$

dans laquelle le rôle des fonctions trigonométriques apparaissant à droite est joué par les harmoniques sphériques et celui de gauche est joué par les polynômes de Legendre .

Le théorème d'addition énonce

${\displaystyle P_{\ell }(\mathbf {x} \cdot \mathbf {y} )={\frac {4\pi }{2\ell +1}}\sum _{m=-\ell }^ {\ell }Y_{\ell m}(\mathbf {y} )\,Y_{\ell m}^{*}(\mathbf {x} )\quad \forall \,\ell \in \mathbb {N } _{0}\;\forall \,\mathbf {x} ,\mathbf {y} \in \mathbb {R} ^{2}\colon \;\|\mathbf {x} \|_{2} =\|\mathbf {y} \|_{2}=1\,,}$

( 1 )

où P _ℓ est le polynôme de Legendre de degré ℓ . Cette expression est valable à la fois pour les harmoniques réelles et complexes. Le résultat peut être prouvé analytiquement, en utilisant les propriétés du noyau de Poisson dans la boule unité, ou géométriquement en appliquant une rotation au vecteur y pour qu'il pointe le long de l' axe z , puis en calculant directement le membre de droite.

En particulier, lorsque x  =  y , cela donne le théorème d'Unsöld

${\displaystyle \sum _{m=-\ell }^{\ell }Y_{\ell m}^{*}(\mathbf {x} )\,Y_{\ell m}(\mathbf {x} ) ={\frac {2\ell +1}{4\pi }}}$

qui généralise l'identité cos ² θ + sin ² thetav = 1 à deux dimensions.

Dans l'expansion ( 1 ), le côté gauche P _ℓ ( x ⋅ y ) est un multiple constant du degré ℓ zonal harmonique sphérique . De ce point de vue, on a la généralisation suivante aux dimensions supérieures. Soit Y _j soit une base orthonormale arbitraire de l'espace H _ℓ de degré ℓ harmoniques sphériques sur le n -sphere. Ensuite , le degré ℓ zonal harmonique correspondant au vecteur unité x , se décompose comme ${\displaystyle Z_{\mathbf {x} }^{(\ell )}}$

${\displaystyle Z_{\mathbf {x} }^{(\ell )}({\mathbf {y} })=\sum _{j=1}^{\dim(\mathbf {H} _{\ell })}{\overline {Y_{j}({\mathbf {x} })}}\,Y_{j}({\mathbf {y} })}$

( 2 )

De plus, l'harmonique zonale est donnée comme un multiple constant du polynôme de Gegenbauer approprié : ${\displaystyle Z_{\mathbf {x} }^{(\ell )}({\mathbf {y} })}$

${\displaystyle Z_{\mathbf {x} }^{(\ell )}({\mathbf {y} })=C_{\ell }^{((n-2)/2)}({\mathbf { x} }\cdot {\mathbf {y} })}$

( 3 )

La combinaison de ( 2 ) et ( 3 ) donne ( 1 ) en dimension n = 2 lorsque x et y sont représentés en coordonnées sphériques. Enfin, évaluer à x = y donne l'identité fonctionnelle

${\displaystyle {\frac {\dim \mathbf {H} _{\ell }}{\omega _{n-1}}}=\sum _{j=1}^{\dim(\mathbf {H} _{\ell })}|Y_{j}({\mathbf {x} })|^{2}}$

où ω _{n −1} est le volume de la ( n −1)-sphère.

Règle de contraction

Une autre identité utile exprime le produit de deux harmoniques sphériques comme une somme sur les harmoniques sphériques

${\displaystyle Y_{a,\alpha }\left(\theta ,\varphi \right)Y_{b,\beta }\left(\theta ,\varphi \right)={\sqrt {\frac {\left( 2a+1\right)\left(2b+1\right)}{4\pi }}}\sum _{c,\gamma }\left(-1\right)^{\gamma }{\sqrt {2c +1}}\gauche({\begin{array}{ccc}a&b&c\\\alpha &\beta &-\gamma \end{array}}\right)\left({\begin{array}{ccc}a&b&c \\0&0&0\end{array}}\right)Y_{c,\gamma }\left(\theta ,\varphi \right)}$

où les valeurs de et sont déterminées par les règles de sélection des symboles 3j . ${\style d'affichage c}$${\style d'affichage \gamma }$

Coefficients de Clebsch-Gordan

Les coefficients de Clebsch-Gordan sont les coefficients apparaissant dans l'expansion du produit de deux harmoniques sphériques en termes d'harmoniques sphériques eux-mêmes. Diverses techniques sont disponibles pour effectuer essentiellement le même calcul, notamment le symbole de Wigner 3-jm , les coefficients de Racah et les intégrales de Slater . De manière abstraite, les coefficients de Clebsch-Gordan expriment le produit tensoriel de deux représentations irréductibles du groupe de rotation comme une somme de représentations irréductibles : convenablement normalisés, les coefficients sont alors les multiplicités.

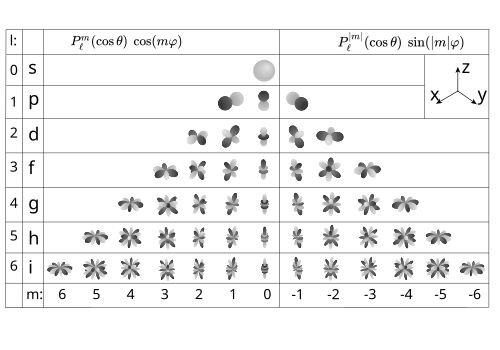
Visualisation des harmoniques sphériques

Les harmoniques sphériques de Laplace peuvent être visualisées en considérant leurs « lignes nodales », c'est-à-dire l'ensemble des points sur la sphère où , ou encore où . Les lignes nodales de sont composées de ℓ cercles : il y a | m | cercles le long des longitudes et ℓ −| m | cercles le long des latitudes. On peut déterminer le nombre de lignes nodales de chaque type en comptant le nombre de zéros dans les directions et respectivement. Considérant en fonction de , les composantes réelle et imaginaire des polynômes de Legendre associés possèdent chacune ℓ −| m | zéros, chacun donnant lieu à une « ligne de latitude » nodale. D'autre part, en considérant en fonction de , les fonctions trigonométriques sin et cos possèdent 2| m | zéros, dont chacun donne lieu à une « ligne de longitude » nodale. ${\displaystyle Y_{\ell }^{m}}$${\displaystyle \Re [Y_{\ell }^{m}]=0}$${\displaystyle \Im [Y_{\ell }^{m}]=0}$${\displaystyle Y_{\ell }^{m}}$${\displaystyle Y_{\ell }^{m}}$${\displaystyle \theta }$${\displaystyle \varphi }$${\displaystyle Y_{\ell }^{m}}$${\displaystyle \theta }$${\displaystyle Y_{\ell }^{m}}$${\displaystyle \varphi }$

Lorsque l'ordre des harmoniques sphériques m est égal à zéro (en haut à gauche sur la figure), les fonctions harmoniques sphériques ne dépendent pas de la longitude et sont appelées zonales . De telles harmoniques sphériques sont un cas particulier de fonctions sphériques zonales . Lorsque ℓ  = | m | (en bas à droite sur la figure), il n'y a pas de passage par zéro en latitude et les fonctions sont dites sectorielles . Pour les autres cas, les fonctions vérifient la sphère, et elles sont appelées tesseral .

Harmoniques sphériques plus généraux de degré ℓ ne sont pas nécessairement celles de la base de Laplace , et leurs ensembles nodaux peuvent être de nature assez générale. ${\displaystyle Y_{\ell }^{m}}$

Liste des harmoniques sphériques

Expressions analytiques pour les premières harmoniques sphériques orthonormalisées de Laplace qui utilisent la convention de phase de Condon-Shortley : ${\displaystyle Y_{\ell }^{m}:S^{2}\to \mathbb {C} }$

Dimensions supérieures

Les harmoniques sphériques classiques sont définies comme des fonctions à valeurs complexes sur la sphère unité à l' intérieur de l'espace euclidien tridimensionnel . Les harmoniques sphériques peuvent être généralisées à l'espace euclidien de dimension supérieure comme suit, conduisant aux fonctions . Laissez P _ℓ représentent l' espace de valeurs complexes polynômes homogènes de degré ℓ en n variables réelles, ici considérées comme des fonctions . Autrement dit, un polynôme p est dans P _ℓ étant entendu que pour tout réel , on a ${\style d'affichage S^{2}}$${\displaystyle \mathbb {R} ^{3}}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle S^{n-1}\to \mathbb {C} }$${\displaystyle \mathbb {R} ^{n}\to \mathbb {C} }$${\displaystyle \lambda \in \mathbb {R} }$

${\displaystyle p(\lambda \mathbf {x} )=\lambda ^{\ell }p(\mathbf {x} ).}$

Soit A _ℓ le sous-espace de P _ℓ constitué de tous les polynômes harmoniques :

${\displaystyle \mathbf {A} _{\ell }:=\{p\in \mathbf {P} _{\ell }\,\mid \,\Delta p=0\}\,.}$

Ce sont les harmoniques sphériques solides (régulières) . Soit H _ℓ l'espace des fonctions sur la sphère unité

${\displaystyle S^{n-1}:=\{\mathbf {x} \in \mathbb {R} ^{n}\,\mid \,\left|x\right|=1\}}$

obtenu par restriction à partir de A _ℓ

${\displaystyle \mathbf {H} _{\ell }:=\left\{f:S^{n-1}\to \mathbb {C} \,\mid \,{\text{ pour certains }}p \in \mathbf {A} _{\ell },\,f(\mathbf {x} )=p(\mathbf {x} ){\text{ pour tout }}\mathbf {x} \in S^{ n-1}\droit\}.}$

Les propriétés suivantes sont valables :

• La somme des espaces H _ℓ est dense dans l'ensemble des fonctions continues sur par rapport à la topologie uniforme , par le théorème de Stone-Weierstrass . De ce fait, la somme de ces espaces est également dense dans l'espace L ² ( S ^{n -1} ) des fonctions carrées intégrables sur la sphère. Ainsi, chaque fonction carrée intégrable sur la sphère se décompose de manière unique en une série d'harmoniques sphériques, où la série converge dans le sens L ² .${\style d'affichage C(S^{n-1})}$${\displaystyle S^{n-1}}$
• Pour tout f  ∈  H _ℓ , on a
  $${\displaystyle \Delta _{S^{n-1}}f=-\ell (\ell +n-2)f.}$$

  
  où Δ _{S ^{n −1}} est l' opérateur de Laplace–Beltrami sur S ^{n −1} . Cet opérateur est l'analogue de la partie angulaire du Laplacien en trois dimensions ; à savoir, le Laplacien en n dimensions se décompose en
  $${\displaystyle \nabla ^{2}=r^{1-n}{\frac {\partial }{\partial r}}r^{n-1}{\frac {\partial }{\partial r}} +r^{-2}\Delta _{S^{n-1}}={\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {n-1} {r}}{\frac {\partiel }{\partiel r}}+r^{-2}\Delta _{S^{n-1}}}$$

  
• Il résulte des théorème de Stokes et la propriété précédente que les espaces H _ℓ sont orthogonaux par rapport au produit scalaire de L ² ( S ^{n -1} ). C'est-à-dire,
  $${\displaystyle \int _{S^{n-1}}f{\bar {g}}\,\mathrm {d} \Omega =0}$$

  
  pour f  ∈  H _ℓ et g  ∈  H _k pour k  ≠  ℓ .
• A l' inverse, les espaces H _ℓ sont précisément les espaces propres de Δ _{S ^{n -1}} . En particulier, une application du théorème spectral au potentiel Riesz donne une autre preuve que les espaces H _ℓ sont orthogonaux deux à deux et complète dans L ² ( S ^{n -1} ).${\displaystyle \Delta _{S^{n-1}}^{-1}}$
• Chaque polynôme homogène p  de  P _{de ℓ} peut être écrit de manière unique sous la forme
  $${\displaystyle p(x)=p_{\ell }(x)+|x|^{2}p_{\ell -2}+\cdots +{\begin{cases}|x|^{\ell }p_ {0}&\ell {\rm {\ pair}}\\|x|^{\ell -1}p_{1}(x)&\ell {\rm {\ impair}}\end{cases}} }$$

  
  où p _j  ∈  A _j . En particulier,
  $${\displaystyle \dim \mathbf {H} _{\ell }={\binom {n+\ell -1}{n-1}}-{\binom {n+\ell -3}{n-1}}. }$$

  

Une base orthogonale d'harmoniques sphériques de dimensions supérieures peut être construite de manière inductive par la méthode de séparation des variables , en résolvant le problème de Sturm-Liouville pour le Laplacien sphérique

${\displaystyle \Delta _{S^{n-1}}=\sin ^{2-n}\varphi {\frac {\partial }{\partial \varphi }}\sin ^{n-2}\varphi {\frac {\partial }{\partial \varphi }}+\sin ^{-2}\varphi \Delta _{S^{n-2}}}$

où φ est la coordonnée axiale dans un repère sphérique sur S ^{n −1} . Le résultat final d'une telle procédure est

${\displaystyle Y_{\ell _{1},\dots \ell _{n-1}}(\theta _{1},\dots \theta _{n-1})={\frac {1}{ \sqrt {2}pi }}}e^{i\ell _{1}\theta _{1}}\prod _{j=2}^{n-1}{}_{j}{\bar { P}}_{\ell _{j}}^{\ell _{j-1}}(\theta _{j})}$

où les indices satisfont | ℓ ₁ | ≤ ℓ ₂ ≤ ⋯ ≤ ℓ _{n −1} et la valeur propre est − ℓ _{n −1} ( ℓ _{n −1} + n −2). Les fonctions du produit sont définies en fonction de la fonction Legendre

${\displaystyle {}_{j}{\bar {P}}_{L}^{\ell }(\theta )={\sqrt {{\frac {2L+j-1}{2}}{\ frac {(L+\ell +j-2)!}{(L-\ell )!}}}}\sin ^{\frac {2-j}{2}}(\theta )P_{L+{\frac {j-2}{2}}}^{-\left(\ell +{\frac {j-2}{2}}\right)}(\cos \theta )\,.}$

Lien avec la théorie des représentations

L'espace H _ℓ des harmoniques sphériques de degré ℓ est une représentation du groupe de symétrie des rotations autour d'un point ( SO(3) ) et de sa double couverture SU(2) . En effet, les rotations agissent sur la sphère bidimensionnelle , et donc aussi sur H _ℓ par composition de fonction

${\displaystyle \psi \mapsto \psi \circ \rho ^{-1}}$

pour ψ une harmonique sphérique et ρ une rotation. La représentation H _ℓ est une représentation irréductible de SO (3).

Les éléments de H _ℓ se présentent comme des restrictions à la sphère des éléments de A _ℓ : polynômes harmoniques homogènes de degré ℓ sur l' espace euclidien tridimensionnel R ³ . Par polarisation de ψ  ∈  A _ℓ , il existe des coefficients symétriques sur les indices, déterminés uniquement par l'exigence ${\displaystyle \psi _{i_{1}\dots i_{\ell }}}$

${\displaystyle \psi (x_{1},\dots ,x_{n})=\sum _{i_{1}\dots i_{\ell }}\psi _{i_{1}\dots i_{\ell }}x_{i_{1}}\cdots x_{i_{\ell }}.}$

La condition que ψ soit harmonique est équivalente à l'affirmation que le tenseur doit être trace libre sur chaque paire d'indices. Ainsi , comme une représentation irréductible de SO (3), H _ℓ est isomorphe à l'espace de traceless tenseurs symétriques de degré ℓ . ${\displaystyle \psi _{i_{1}\dots i_{\ell }}}$

Plus généralement, les états analogues tiennent dans des dimensions supérieures: l'espace H _ℓ d'harmoniques sphériques sur la n -sphere est la représentation irréductible de SO ( n + 1) correspondant aux traceless symétriques ℓ -tensors. Cependant, alors que chaque représentation tensorielle irréductible de SO(2) et SO(3) est de ce type, les groupes orthogonaux spéciaux dans les dimensions supérieures ont des représentations irréductibles supplémentaires qui ne surviennent pas de cette manière.

Les groupes orthogonaux spéciaux ont des représentations de spin supplémentaires qui ne sont pas des représentations tensorielles et ne sont généralement pas des harmoniques sphériques. Une exception est la représentation de spin de SO(3) : à proprement parler ce sont des représentations de la double couverture SU(2) de SO(3). À son tour, SU(2) est identifié avec le groupe des quaternions unitaires , et coïncide ainsi avec la 3-sphère . Les espaces des harmoniques sphériques sur la 3-sphère sont certaines représentations de spin de SO(3), par rapport à l'action par multiplication quaternionique.

Connexion avec des harmoniques hémisphériques

Les harmoniques sphériques peuvent être séparées en deux ensembles de fonctions. Il s'agit des fonctions hémisphériques (HSH), orthogonales et complètes sur l'hémisphère. Un autre est celui des harmoniques hémisphériques complémentaires (CHSH).

Généralisations

Les symétries préservant l'angle des deux sphères sont décrites par le groupe de transformations de Möbius PSL(2, C ). Par rapport à ce groupe, la sphère est équivalente à la sphère de Riemann habituelle . Le groupe PSL(2, C ) est isomorphe au (propre) groupe de Lorentz , et son action sur la sphère à deux est en accord avec l'action du groupe de Lorentz sur la sphère céleste dans l'espace de Minkowski . L'analogue des harmoniques sphériques pour le groupe de Lorentz est donné par la série hypergéométrique ; de plus, les harmoniques sphériques peuvent être réexprimées en termes de séries hypergéométriques, car SO(3) = PSU(2) est un sous - groupe de PSL(2, C ).

Plus généralement, les séries hypergéométriques peuvent être généralisées pour décrire les symétries de tout espace symétrique ; en particulier, des séries hypergéométriques peuvent être développées pour n'importe quel groupe de Lie .

Voir également

Remarques

Les références

Références citées

• Courant, Richard ; Hilbert, David (1962), Méthodes de physique mathématique, Volume I , Wiley-Interscience.
• Edmonds, AR (1957), Momentum angulaire en mécanique quantique , Princeton University Press, ISBN 0-691-07912-9
• Eremenko, Alexandre ; Jakobson, Dmitry ; Nadirashvili, Nikolai (2007), "On nodal sets and nodal domains on S² and R²" , Annales de l'Institut Fourier , 57 (7) : 2345-2360, doi : 10.5802/aif.2335 , ISSN  0373-0956 , MR  2394544
• Hall, Brian C. (2013), Quantum Theory for Mathematicians , Graduate Texts in Mathematics, 267 , Springer, ISBN 978-1461471158
• MacRobert, TM (1967), Harmoniques sphériques: Un traité élémentaire sur les fonctions harmoniques, avec applications , Pergamon Press.
• Meijer, Paul Herman Ernst; Bauer, Edmond (2004), Théorie des groupes : L'application à la mécanique quantique , Douvres, ISBN 978-0-486-43798-9.
• Solomentsev, ED (2001) [1994], "Spherical harmonics" , Encyclopedia of Mathematics , EMS Press.
• Stein, Elias ; Weiss, Guido (1971), Introduction à l'analyse de Fourier sur les espaces euclidiens , Princeton, NJ: Princeton University Press, ISBN 978-0-691-08078-9.
• Unsöld, Albrecht (1927), "Beiträge zur Quantenmechanik der Atome", Annalen der Physik , 387 (3) : 355–393, Bibcode : 1927AnP...3873..355U , doi : 10.1002/andp.19273870304.
• Whittaker, ET ; Watson, GN (1927), A Course of Modern Analysis , Cambridge University Press , p. 392.

Références générales

• EW Hobson, La théorie des harmoniques sphériques et ellipsoïdales , (1955) Chelsea Pub. Co., ISBN  978-0-8284-0104-3 .
• C. Müller, Spherical Harmonics , (1966) Springer, Lecture Notes in Mathematics, Vol. 17, ISBN  978-3-540-03600-5 .
• EU Condon et GH Shortley, The Theory of Atomic Spectra , (1970) Cambridge at the University Press, ISBN  0-521-09209-4 , Voir chapitre 3 .
• JD Jackson, Électrodynamique classique , ISBN  0-471-30932-X
• Albert Messiah, Mécanique quantique , tome II. (2000) Douvres. ISBN  0-486-40924-4 .
• Appuyez sur, WH; Teukolsky, SA; Vetterling, WT ; Flannery, BP (2007), "Section 6.7. Harmoniques sphériques" , Recettes numériques : L'art de l'informatique scientifique (3e éd.), New York : Cambridge University Press, ISBN 978-0-521-88068-8
• DA Varshalovich, AN Moskalev, VK Khersonskii Quantum Theory of Angular Momentum , (1988) World Scientific Publishing Co., Singapour, ISBN  9971-5-0107-4
• Weisstein, Eric W. "Harmoniques sphériques" . MathWorld .
• Maddock, John, Harmoniques sphériques dans Boost.Math