Sous-groupe - Subgroup

Structure algébrique → Théorie des groupes Théorie des groupes
Notions de base Sous-groupe Sous-groupe normal Groupe de quotients Produit (semi-) direct Homomorphismes de groupe noyau image somme directe produit de couronne Facile fini infini continu multiplicatif additif cyclique abélien dièdre nilpotent soluble action Glossaire de la théorie des groupes Liste des sujets de théorie des groupes
Groupes finis Classification des groupes simples finis cyclique en alternance Type de mensonge sporadique Le théorème de Cauchy Le théorème de Lagrange Théorèmes de Sylow théorème de Hall groupe p Groupe abélien élémentaire Groupe Frobenius Multiplicateur de Schur Groupe symétrique S n Klein quatre groupe V Groupe dièdre D n Groupe de quaternions Q Groupe dicyclique Dic n
Groupes discrets Treillis Entiers ( )${\displaystyle \mathbb {Z} }$ Groupe gratuit Groupes modulaires PSL(2, )${\displaystyle \mathbb {Z} }$ SL(2, )${\displaystyle \mathbb {Z} }$ Groupe arithmétique Treillis Groupe hyperbolique
Groupes topologiques et de Lie Solénoïde Cercle GL linéaire général ( n ) Linéaire spécial SL( n ) O orthogonal ( n ) Euclidienne E( n ) Spécial orthogonal SO( n ) Unitaire U( n ) Unité spéciale SU( n ) Sp symplectique ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Conforme Difféomorphisme Boucle Groupe de Lie de dimension infinie O(∞) SU(∞) Sp(∞)
Groupes algébriques Groupe algébrique linéaire Groupe réducteur Variété abélienne Courbe elliptique
v t e

En théorie des groupes , branche des mathématiques , étant donné un groupe G sous une opération binaire  ∗, un sous - ensemble H de G est appelé un sous - groupe de G si H forme également un groupe sous l'opération ∗. Plus précisément, H est un sous-groupe de G si la restriction de à H × H est une opération de groupe sur H . Ceci est habituellement notée H ≤ G , lire « H est un sous - groupe de G ».

Le sous - groupe trivial de tout groupe est le sous-groupe { e } constitué uniquement de l'élément d'identité.

Un sous - groupe convenable d'un groupe G est un sous - groupe H qui est un sous - ensemble de G (qui est, H ≠ G ). Ceci est généralement représenté notationnellement par H < G , lu comme " H est un sous-groupe propre de G ". Certains auteurs excluent également le groupe trivial d'être propre (c'est-à-dire H { e }).

Si H est un sous-groupe de G , alors G est parfois appelé un surgroupe de H .

Les mêmes définitions s'appliquent plus généralement lorsque G est un semi - groupe arbitraire , mais cet article ne traitera que des sous-groupes de groupes. Le groupe G est parfois désigné par la paire ordonnée ( G , ) , généralement pour souligner l'opération lorsque G porte plusieurs structures algébriques ou autres.

Propriétés de base des sous-groupes

• Un sous-ensemble H du groupe G est un sous-groupe de G si et seulement s'il est non vide et clos par produits et inverses. (Les conditions de fermeture signifient ce qui suit : chaque fois que a et b sont dans H , alors ab et a ⁻¹ sont également dans H . Ces deux conditions peuvent être combinées en une seule condition équivalente : chaque fois que a et b sont dans H , alors ab ⁻¹ est aussi dans H .) Dans le cas où H est fini, alors H est un sous - groupe si et seulement si H est fermé par produits. (Dans ce cas, chaque élément a de H génère un sous-groupe cyclique fini de H , et l'inverse de a est alors a ⁻¹ = a ^{n −1} , où n est l'ordre de a .)
• La condition ci-dessus peut être énoncée en termes d' homomorphisme ; c'est-à-dire que H est un sous-groupe d'un groupe G si et seulement si H est un sous-ensemble de G et qu'il existe un homomorphisme d'inclusion (c'est-à-dire i( a ) = a pour tout a ) de H à G .
• L' identité d'un sous-groupe est l'identité du groupe : si G est un groupe d'identité e _G , et H est un sous-groupe de G d'identité e _H , alors e _H = e _G .
• L' inverse d'un élément d'un sous-groupe est l'inverse de l'élément du groupe : si H est un sous-groupe d'un groupe G , et a et b sont des éléments de H tels que ab = ba = e _H , alors ab = ba = e _G .
• L' intersection des sous-groupes A et B est à nouveau un sous-groupe. L' union des sous-groupes A et B est un sous-groupe si et seulement si A ou B contient l'autre, puisque par exemple 2 et 3 sont dans l'union de 2Z et 3Z mais leur somme 5 ne l'est pas. Un autre exemple est l'union de l'axe des x et de l'axe des y dans le plan (avec l'opération d'addition) ; chacun de ces objets est un sous-groupe mais leur union ne l'est pas. Cela sert également d'exemple de deux sous-groupes, dont l'intersection est précisément l'identité.
• Si S est un sous-ensemble de G , alors il existe un sous-groupe minimum contenant S , qui peut être trouvé en prenant l'intersection de tous les sous-groupes contenant S ; il est noté ⟨ S ⟩ et est dit être le sous - groupe engendré par S . Un élément de G est dans ⟨ S ⟩ si et seulement si c'est un produit fini d'éléments de S et de leurs inverses.
• Tout élément a d'un groupe G engendre le sous-groupe cyclique ⟨ a ⟩. Si ⟨ a ⟩ est isomorphe à Z / n Z pour un entier positif n , alors n est le plus petit entier positif pour lequel a ⁿ = e , et n est appelé l' ordre de a . Si ⟨ a ⟩ est isomorphe à Z , alors a est dit d' ordre infini .
• Les sous-groupes d'un groupe donné forment un réseau complet sous inclusion, appelé réseau des sous-groupes . (Alors que l' infimum est ici l'intersection théorique des ensembles habituelle, le supremum d'un ensemble de sous-groupes est le sous-groupe généré par l'union théorique des ensembles des sous-groupes, et non l'union théorique des ensembles elle-même.) Si e est l'identité de G , alors le groupe trivial { e } est le sous-groupe minimum de G , tandis que le sous-groupe maximum est le groupe G lui-même.

Cosets et le théorème de Lagrange

Étant donné un sous-groupe H et un certain a dans G, nous définissons le coset gauche aH = { ah  : h dans H }. Comme a est inversible, l'application φ : H → aH donnée par φ( h ) = ah est une bijection . De plus, chaque élément de G est contenu dans précisément un co-ensemble gauche de H ; les cosets de gauche sont les classes d'équivalence correspondant à la relation d'équivalence a ₁ ~ a ₂ si et seulement si a ₁ ⁻¹ a ₂ est dans H . Le nombre de classes gauches de H est appelé l' indice de H dans G et est noté [ G  : H ].

Le théorème de Lagrange énonce que pour un groupe fini G et un sous-groupe H ,

${\style d'affichage [G:H]={|G| \sur |H|}}$

où | G | et | H | désignent respectivement les ordres de G et H . En particulier, l'ordre de chaque sous-groupe de G (et l'ordre de chaque élément de G ) doit être un diviseur de | G |.

Les bons cosets sont définis de manière analogue : Ha = { ha  : h dans H }. Ce sont aussi les classes d'équivalence pour une relation d'équivalence appropriée et leur nombre est égal à [ G  : H ].

Si aH = Ha pour tout a dans G , alors H est dit un sous - groupe normal . Chaque sous-groupe d'indice 2 est normal : les co-ensembles de gauche, ainsi que les co-ensembles de droite, sont simplement le sous-groupe et son complément. Plus généralement, si p est le plus petit nombre premier divisant l'ordre d'un groupe fini G, alors tout sous-groupe d'indice p (s'il existe) est normal.

Exemple : Sous-groupes de Z ₈

Soit G le groupe cyclique Z ₈ dont les éléments sont

${\displaystyle G=\gauche\{0,4,2,6,1,5,3,7\droit\}}$

et dont l'opération de groupe est l' addition modulo huit . Sa table Cayley est

+	0	4	2	6	1	5	3	7
0	0	4	2	6	1	5	3	7
4	4	0	6	2	5	1	7	3
2	2	6	4	0	3	7	5	1
6	6	2	0	4	7	3	1	5
1	1	5	3	7	2	6	4	0
5	5	1	7	3	6	2	0	4
3	3	7	5	1	4	0	6	2
7	7	3	1	5	0	4	2	6

Ce groupe a deux sous-groupes non triviaux : J ={0,4} et H ={0,4,2,6} , où J est également un sous-groupe de H . La table de Cayley pour H est le quadrant supérieur gauche de la table de Cayley pour G ; La table de Cayley pour J est le quadrant supérieur gauche de la table de Cayley pour H . Le groupe G est cyclique , de même que ses sous-groupes. En général, les sous-groupes de groupes cycliques sont également cycliques.

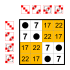
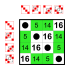
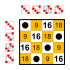
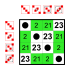
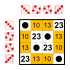
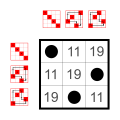
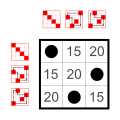
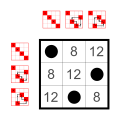
Exemple : Sous-groupes de S ₄ (le groupe symétrique sur 4 éléments)

Chaque groupe a autant de petits sous-groupes que d'éléments neutres sur la diagonale principale :

Le groupe trivial et les groupes à deux éléments Z ₂ . Ces petits sous-groupes ne sont pas comptés dans la liste suivante.

Le groupe symétrique S 4 montrant toutes les permutations de 4 éléments

Tous les 30 sous-groupes Simplifié Diagrammes de Hasse du réseau de sous - groupes de S 4

12 éléments

8 éléments

Groupe dièdre d'ordre 8 Sous-groupes :

Groupe dièdre d'ordre 8 Sous-groupes :

Groupe dièdre d'ordre 8 Sous-groupes :

6 éléments

Groupe symétrique S 3 Sous-groupe :

Groupe symétrique S 3 Sous-groupe :

Groupe symétrique S 3 Sous-groupe :

Groupe symétrique S 3 Sous-groupe :

4 éléments

Klein quatre-groupe

Klein quatre-groupe

Klein quatre-groupe

Klein quatre-groupe

Groupe cyclique Z 4

Groupe cyclique Z 4

Groupe cyclique Z 4

3 éléments

Groupe cyclique Z 3

Groupe cyclique Z 3

Groupe cyclique Z 3

Groupe cyclique Z 3

Autres exemples

• Les entiers pairs sont un sous-groupe du groupe additif d'entiers : lorsque vous additionnez deux nombres pairs, vous obtenez un nombre pair.
• Un idéal dans un anneau est un sous-groupe du groupe additif de .${\style d'affichage R}$${\style d'affichage R}$
• Un sous - espace linéaire d'un espace vectoriel est un sous-groupe du groupe additif de vecteurs.
• Soit un groupe abélien ; les éléments de qui ont une période finie forment un sous-groupe de appelé le sous - groupe de torsion de .${\style d'affichage A}$${\style d'affichage A}$${\style d'affichage A}$${\style d'affichage A}$

Voir également

• Sous-groupe Cartan
• Sous-groupe de raccords
• Sous-groupe stable
• Sous-groupe virgule fixe
• Test de sous-groupe

Remarques

Les références

• Jacobson, Nathan (2009), Algèbre de base , 1 (2e éd.), Douvres, ISBN 978-0-486-47189-1.
• Hungerford, Thomas (1974), Algèbre (1ère éd.), Springer-Verlag, ISBN 9780387905181.
• Artin, Michael (2011), Algèbre (2e éd.), Prentice Hall, ISBN 9780132413770.
• Dummit, David S.; Foote, Richard M. (2004). Algèbre abstraite (3e éd.). Hoboken, New Jersey : Wiley. ISBN 9780471452348. OCLC  248917264 .