Logique temporelle - Temporal logic

En logique , la logique temporelle est tout système de règles et de symbolisme pour représenter et raisonner sur des propositions qualifiées en termes de temps (par exemple, " j'ai toujours faim ", " j'aurai éventuellement faim " ou " j'aurai faim jusqu'à ce que je mange quelque chose"). Il est parfois également utilisé pour désigner la logique des temps , un système de logique temporelle basé sur la logique modale introduit par Arthur Prior à la fin des années 1950, avec d'importantes contributions de Hans Kamp . Il a été développé par des informaticiens , notamment Amir Pnueli , et des logiciens .

La logique temporelle a trouvé une application importante dans la vérification formelle , où elle est utilisée pour énoncer les exigences des systèmes matériels ou logiciels. Par exemple, on peut souhaiter dire que chaque fois qu'une demande est faite, l'accès à une ressource est finalement accordé, mais il n'est jamais accordé à deux demandeurs simultanément. Une telle déclaration peut commodément être exprimée dans une logique temporelle.

Motivation

Considérez l'énoncé « J'ai faim ». Bien que sa signification soit constante dans le temps, la valeur de vérité de l'énoncé peut varier dans le temps. Parfois c'est vrai, parfois faux, mais jamais à la fois vrai et faux. Dans une logique temporelle, un énoncé peut avoir une valeur de vérité qui varie dans le temps, contrairement à une logique atemporelle, qui ne s'applique qu'aux énoncés dont les valeurs de vérité sont constantes dans le temps. Ce traitement de la valeur de vérité dans le temps différencie la logique temporelle de la logique verbale computationnelle .

La logique temporelle a toujours la capacité de raisonner sur une chronologie. Les « logiques temporelles » dites linéaires sont restreintes à ce type de raisonnement. Les logiques de branchement, cependant, peuvent raisonner sur plusieurs chronologies. Cela présuppose un environnement qui peut agir de manière imprévisible. Pour continuer l'exemple, dans une logique de branchement, nous pouvons affirmer qu'"il y a une possibilité que je reste affamé pour toujours", et qu'"il y a une possibilité que finalement je n'aie plus faim". Si nous ne savons pas si je serai un jour nourri, ces affirmations peuvent toutes les deux être vraies.

Histoire

Bien que la logique d' Aristote soit presque entièrement concernée par la théorie du syllogisme catégorique , il y a des passages dans son travail qui sont maintenant considérés comme des anticipations de la logique temporelle, et peuvent impliquer une forme précoce et partiellement développée de logique binaire modale temporelle du premier ordre. . Aristote s'est particulièrement intéressé au problème des contingents futurs , où il ne pouvait accepter que le principe de bivalence s'applique aux énoncés concernant des événements futurs, c'est-à-dire que nous pouvons actuellement décider si un énoncé concernant un événement futur est vrai ou faux, comme « il sera une bataille navale demain".

Il y a eu peu de développement pendant des millénaires, a noté Charles Sanders Peirce au 19ème siècle :

Le temps a généralement été considéré par les logiciens comme ce qu'on appelle la matière « extralogique ». Je n'ai jamais partagé cet avis. Mais j'ai pensé que la logique n'était pas encore parvenue à l'état de développement où l'introduction de modifications temporelles de ses formes n'entraînerait pas une grande confusion ; et je suis encore beaucoup de cette façon de penser.

Étonnamment pour Peirce , le premier système de logique temporelle a été construit, pour autant que nous le sachions, dans la première moitié du 20e siècle. Bien qu'Arthur Prior soit largement connu comme un fondateur de la logique temporelle, la première formalisation d'une telle logique a été fournie en 1947 par le logicien polonais Jerzy Łoś . Dans son ouvrage Podstawy Analizy Metodologicznej Kanonów Milla ( Les fondements d'une analyse méthodologique des méthodes de Mill ) il a présenté une formalisation des canons de Mill . Dans Łoś .' l'accent a été mis sur le facteur temps. Ainsi, pour atteindre son but, il a dû créer une logique qui pourrait fournir des moyens de formalisation des fonctions temporelles. La logique peut être considérée comme un sous - produit de Łoś « objectif principal, mais il a été la première logique de position qui, en tant que cadre a ensuite été utilisé pour los » invetions en logique épistémique. La logique elle-même a une syntaxe très différente de la logique du temps de Prior, qui utilise des opérateurs modaux. Le langage de la logique Łoś ' utilise plutôt un opérateur de réalisation spécifique pour la logique positionnelle qui lie l'expression au contexte spécifique dans lequel sa valeur de vérité est considérée. Dans le travail de Łoś ', ce contexte considéré n'était que temporel, ainsi les expressions étaient liées à des moments ou à des intervalles de temps spécifiques.

Dans les années suivantes, les recherches sur la logique temporelle d' Arthur Prior ont commencé. Il s'inquiétait des implications philosophiques du libre arbitre et de la prédestination . Selon sa femme, il a envisagé pour la première fois de formaliser la logique temporelle en 1953. Les résultats de ses recherches ont été présentés pour la première fois à la conférence de Wellington en 1954. Le système Prior présenté était similaire du point de vue syntaxique à la logique Łoś , bien que ce n'est qu'en 1955 qu'il a explicitement fait référence à oś ', dans la dernière section de l'annexe 1 de Prior's Formal Logic.

Prior a donné des conférences sur le sujet à l' Université d'Oxford en 1955-1956, et en 1957 a publié un livre, Time and Modality , dans lequel il a introduit une logique modale propositionnelle avec deux connecteurs temporels ( opérateurs modaux ), F et P, correspondant à "un jour dans le futur" et "un jour dans le passé". Dans ces premiers travaux, Prior considérait le temps comme linéaire. En 1958 cependant, il reçoit une lettre de Saul Kripke , qui lui fait remarquer que cette hypothèse est peut-être injustifiée. Dans un développement qui préfigurait un développement similaire en informatique, Prior a pris cela en considération et a développé deux théories du temps de branchement, qu'il a appelées "Ockhamist" et "Peircean". Entre 1958 et 1965, Prior a également correspondu avec Charles Leonard Hamblin , et un certain nombre de premiers développements dans le domaine peuvent être attribués à cette correspondance, par exemple les implications de Hamblin . Prior a publié son ouvrage le plus abouti sur le sujet, le livre Past, Present, and Future en 1967. Il est décédé deux ans plus tard.

Avec la logique tendue, Prior a construit quelques systèmes de logique positionnelle , qui ont hérité des idées principales de Łoś . Les travaux sur les logiques temporelles positionnelles ont été poursuivis par Nicholas Rescher dans les années 60 et 70. Dans des ouvrages tels que Note on Chronological Logic (1966), On the Logic of Chronological Propositions (1968) , Topological Logic (1968), Temporal Logic (1971), il a recherché les liens entre les systèmes de Łoś et de Prior . De plus , il a prouvé que les opérateurs de temps de Prior pouvaient être définis en utilisant l' opérateur de réalisation dans des logiques positionnelles spécifiques . Rescher dans son travail a également créé des systèmes plus généraux de logiques positionnelles . Bien que les premiers aient été construits pour des usages purement temporels, il a proposé un terme de logiques topologiques censé contenir un opérateur de réalisation mais n'avait pas d'axiomes temporels spécifiques - comme l'axiome de l'horloge.

Les opérateurs temporels binaires Depuis et Jusqu'à ont été introduits par Hans Kamp dans son doctorat de 1968. thèse, qui contient également un résultat important reliant la logique temporelle à la logique du premier ordre - un résultat maintenant connu sous le nom de théorème de Kamp .

Deux des premiers concurrents dans les vérifications formelles étaient la logique temporelle linéaire , une logique temporelle linéaire d' Amir Pnueli , et la logique d'arbre de calcul , une logique temporelle ramifiée par Mordechai Ben-Ari , Zohar Manna et Amir Pnueli. Un formalisme presque équivalent à CTL a été suggéré à peu près au même moment par EM Clarke et EA Emerson . Le fait que la seconde logique puisse être décidée plus efficacement que la première ne reflète pas les logiques de branchement et linéaires en général, comme cela a parfois été avancé. Au contraire, Emerson et Lei montrent que toute logique linéaire peut être étendue à une logique de branchement qui peut être décidée avec la même complexité.

oś' logique positionnelle

La logique de Łoś a été publiée sous le titre de sa thèse de maîtrise en 1947 en polonais. Ses concepts philosophiques et formels pourraient être considérés comme la continuation de l'école de logique de Lviv-Varsovie car son superviseur était Jerzy Słupecki, disciple de Jan Łukasiewicz. L'article n'a été traduit en anglais qu'en 1977, bien qu'Henryk Hiż ait présenté en 1951 une revue brève mais informative dans le Journal of Symbolic Logic . Sa revue contenait les concepts fondamentaux de son travail et était suffisante pour vulgariser les résultats de Łoś parmi la communauté logique. L'objectif principal de ce travail était de présenter les canons de Mill dans le cadre de la logique formelle. Pour atteindre cet objectif, l'auteur a étudié l'importance des fonctions temporelles dans la structure du concept de Miil. Ayant cela, il a fourni son système axiomatique de logique qui s'adapterait comme un cadre pour les canons de Mill avec leurs aspects temporels.

Syntaxe

Le langage de la logique publié pour la première fois dans Podstawy Analizy Metodologicznej Kanonów Milla ( Les fondements d'une analyse méthodologique des méthodes de Mill ) se composait de :

• opérateurs logiques du premier ordre '¬', '∧', '∨', '→', '≡', '∀' et '∃'
• opérateur de réalisation U
• symbole fonctionnel
• variables propositionnelles p ₁ ,p ₂ ,p ₃ ,...
• variables désignant les moments t ₁ ,t ₂ ,t ₃ ,...
• variables désignant des intervalles de temps n ₁ ,n ₂ ,n ₃ ,...

L'ensemble de termes (noté S) est construit comme suit :

• les variables désignant des moments ou des intervalles de temps sont des termes
• si et est une variable d'intervalle de temps, alors${\displaystyle \tau \in S}$${\style d'affichage \epsilon }$${\displaystyle \delta (\tau ,\epsilon )\in S}$

L'ensemble de formules (noté For) est construit comme suit :

• toutes les formules logiques du premier ordre sont valides
• si et est une variable propositionnelle, alors${\displaystyle \tau \in S}$${\style d'affichage \phi }$${\displaystyle U_{\tau }(\phi )\in Pour}$
• si , alors${\displaystyle \phi \in Pour}$${\displaystyle \neg \phi \in Pour}$
• si et , alors${\displaystyle \phi ,\psi \in Pour}$${\displaystyle \circ \in \{\wedge ,\vee ,\rightarrow ,\equiv \}}$${\displaystyle \phi \circ \psi \in Pour}$
• si et et est une variable propositionnelle, de moment ou d'intervalle, alors${\displaystyle \phi \in Pour}$${\displaystyle Q\in \{\forall ,\existe \}}$${\displaystyle Q_{\upsilon }\phi \in Pour}$

Système Axiomatique d'origine

1. ${\displaystyle U_{t_{1}}\neg p_{1}\equiv \neg U_{t_{1}}p_{1}}$
2. ${\displaystyle U_{t_{1}}(p_{1}\rightarrow p_{2})\rightarrow (U_{t_{1}}p_{1}\rightarrow U_{t_{1}}p_{2}) }$
3. ${\displaystyle U_{t_{1}}((p_{1}\rightarrow p_{2})\rightarrow ((p_{2}\rightarrow p_{3})\rightarrow (p_{1}\rightarrow p_{3 })))}$
4. ${\displaystyle U_{t_{1}}(p_{1}\rightarrow (\neg p_{1}\rightarrow p_{2}))}$
5. ${\displaystyle U_{t_{1}}((\neg p_{1}\rightarrow p_{1})\rightarrow p_{1})}$
6. ${\displaystyle \forall _{t_{1}}U_{t_{1}}p_{1}\rightarrow p_{1}}$
7. ${\displaystyle \forall _{t_{1}}\forall _{n_{1}}\exists _{t_{2}}\forall _{p_{1}}(U_{\delta (t_{1}, n_{1})}p_{1}\équiv U_{t_{2}}p_{1})}$
8. ${\displaystyle \forall _{t_{1}}\forall _{n_{1}}\exists _{t_{2}}\forall _{p_{1}}(U_{\delta (t_{2}, n_{1})}p_{1}\équiv U_{t_{1}}p_{1})}$
9. ${\displaystyle \forall _{t_{1}}\exists _{p_{1}}\forall _{t_{2}}(U_{t_{2}}p_{1}\equiv \forall _{p_{ 2}}(U_{t_{1}}p_{2}\équivalent U_{t_{2}}p_{2}))}$

Logique du temps de Prior (TL)

La logique du temps phrastique introduite dans Time and Modality a quatre opérateurs modaux (non fonctionnels en vérité ) (en plus de tous les opérateurs fonctionnels en vérité habituels dans la logique propositionnelle du premier ordre .

• P : "C'était le cas que..." (P signifie "passé")
• F : "Ce sera le cas que..." (F signifie "futur")
• G : "Ce sera toujours le cas que..."
• H : "Ça a toujours été le cas que..."

Ceux-ci peuvent être combinés si on laisse π un chemin infini :

• ${\displaystyle \pi \vDash FG\phi }$: "À un certain point, est vrai à tous les états futurs du chemin"${\style d'affichage \phi }$
• ${\displaystyle \pi \vDash GF\phi }$: " est vrai à une infinité d'états sur le chemin"${\style d'affichage \phi }$

A partir de P et F on peut définir G et H , et vice versa :

${\displaystyle {\begin{aligned}F&\equiv \lnot G\lnot \\P&\equiv \lnot H\lnot \end{aligned}}}$

Syntaxe et sémantique

Une syntaxe minimale pour TL est spécifiée avec la grammaire BNF suivante :

${\displaystyle \phi ,\psi ::=a\;|\;\bot \;|\;\lnot \phi \;|\;\phi \lor \psi \;|\;G\phi \;| \;H\phi }$

où a est une formule atomique .

Les modèles de Kripke sont utilisés pour évaluer la vérité des phrases en TL. Une paire ( T , <) d'un ensemble T et d'une relation binaire < sur T (appelée "précédence") est appelée une trame . Un modèle est donné par le triple ( T , <, V ) d'un cadre et une fonction V appelée une évaluation qui attribue à chaque paire ( a , u ) d'une formule atomique et d'une valeur temporelle une valeur de vérité. La notion " ϕ est vraie dans un modèle U =( T , <, V ) à l'instant u " est abrégée U ⊨ ϕ [ u ]. Avec cette notation,

Déclaration	... est vrai juste quand
U ⊨ a [ u ]	V ( a , u )=vrai
U ⊨¬ ϕ [ u ]	pas U ⊨ ϕ [ u ]
U ⊨( ϕ ∧ ψ )[ u ]	U de la φ [ u ] et U ⊨ ψ [ u ]
U ⊨( ϕ ∨ ψ )[ u ]	U ⊨ ϕ [ u ] ou U ⊨ ψ [ u ]
U ⊨( ϕ → ψ )[ u ]	U de la ψ [ u ] si U de la φ [ u ]
U G ϕ [ u ]	U ⊨ ϕ [ v ] pour tout v avec u < v
U ⊨H ϕ [ u ]	U ⊨ ϕ [ v ] pour tout v avec v < u

Étant donné une classe F de cadres, une phrase φ de TL est

• valide par rapport à F si , pour chaque modèle U = ( T , <, V ) avec ( T , <) à F et pour chaque u en T , U ⊨ & phiv [ u ]
• satisfiable par rapport à F s'il existe un modèle U =( T ,<, V ) avec ( T ,<) dans F tel que pour un certain u dans T , U ⊨ ϕ [ u ]
• une conséquence d'une phrase ψ par rapport à F si , pour chaque modèle U = ( T , <, V ) avec ( T , <) à F et pour chaque u en T , si U de la ψ [ u ], puis U ⊨ & phiv [ tu ]

De nombreuses phrases ne sont valables que pour une classe limitée de cadres. Il est courant de restreindre la classe des cadres à ceux avec une relation < qui est transitive , antisymétrique , réflexive , trichotomique , irréflexive , totale , dense , ou une combinaison de celles-ci.

Une logique axiomatique minimale

Burgess décrit une logique qui ne fait aucune hypothèse sur la relation <, mais permet des déductions significatives, basées sur le schéma d'axiome suivant :

1. A où A est une tautologie de la logique du premier ordre
2. G ( A → B ) → (G A → G B )
3. H( A → B )→(HA A →H B )
4. A →GP A
5. A →HF A

avec les règles de déduction suivantes :

1. étant donné A → B et A , en déduire B ( modus ponens )
2. étant donné une tautologie A , en déduire G A
3. étant donné une tautologie A , en déduire H A

On peut en déduire les règles suivantes :

1. Règle de Becker : étant donné A → B , en déduire T A →T B où T est un temps , toute suite composée de G, H, F et P.
2. Miroir : étant donné un théorème A , en déduire son énoncé miroir A ^§ , qui s'obtient en remplaçant G par H (et donc F par P) et vice versa.
3. Dualité : étant donné un théorème A , en déduire son énoncé dual A *, qui s'obtient en intervertissant ∧ avec ∨, G avec F et H avec P.

Traduction en logique des prédicats

Burgess donne une traduction Meredith des déclarations en TL en déclarations en logique du premier ordre avec une variable libre x ₀ (représentant le moment présent). Cette translation M est définie récursivement comme suit :

${\displaystyle {\begin{aligned}&M(a)&&=a^{*}x_{0}\\&M(\lnot \phi )&&=\lnot M(\phi )\\&M(\phi \land \psi )&&=M(\phi )\land M(\psi )\\&M({\mathsf {G}}\phi )&&=\forall x_{1}(x_{0}<x_{1}\ rightarrow M(A^{+}))\\&M({\mathsf {H}}\phi )&&=\forall x_{1}(x_{1}<x_{0}\rightarrow M(A^{+ }))\end{aligné}}}$

où est la phrase avec tous les indices variables incrémentés de 1 et est un prédicat à une place défini par . ${\style d'affichage A^{+}}$${\style d'affichage A}$${\displaystyle a^{*}}$${\displaystyle x\mapsto V(a,x)}$

Opérateurs temporels

La logique temporelle a deux sortes d'opérateurs : les opérateurs logiques et les opérateurs modaux [1] . Les opérateurs logiques sont des opérateurs fonctionnels de vérité usuels ( ). Les opérateurs modaux utilisés en logique temporelle linéaire et en logique d'arbre de calcul sont définis comme suit. ${\displaystyle \neg ,\lor ,\land ,\rightarrow }$

Textuel	Symbolique	Définition	Explication	Diagramme
Opérateurs binaires
φ U ψ	${\displaystyle \phi ~{\mathcal {U}}~\psi }$	${\displaystyle (B\,{\mathcal {U}}\,C)(\phi )=\ (\exists i:C(\phi _{i})\land (\forall j<i:B(\ phi _{j})))}$	U usqu'à: ψ tient au courant ou une position future, et φ doit tenir jusqu'à cette position. A cette position φ ne doit pas contenir plus.
φ R ψ	${\displaystyle \phi ~{\mathcal {R}}~\psi }$	${\displaystyle (B\,{\mathcal {R}}\,C)(\phi )=\ (\forall i:C(\phi _{i})\lor (\exists j<i:B(\ phi _{j})))}$	R depresse: & phiv libère ψ si ψ est vrai jusqu'à et y compris la première position dans laquelle φ est vrai (ou pour toujours si la position d'un tel n'existe pas).
Opérateurs unaires
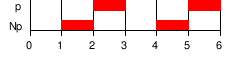
N φ	${\style d'affichage \bigcirc \phi }$	${\displaystyle {\mathcal {N}}B(\phi _{i})=B(\phi _{i+1})}$	N ext : φ doit tenir à l'état suivant. ( X est utilisé comme synonyme.)
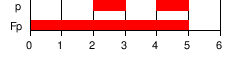
F φ	${\displaystyle \Diamond \phi }$	${\displaystyle {\mathcal {F}}B(\phi )=(true\,{\mathcal {U}}\,B)(\phi )}$	F FUTURS: φ a finalement attente (quelque part sur le chemin suivant).
G φ	${\displaystyle \Box \phi }$	${\displaystyle {\mathcal {G}}B(\phi )=\neg {\mathcal {F}}\neg B(\phi )}$	G lobally: φ doit tenir sur tout le trajet suivant.
A φ	${\displaystyle \forall \phi }$	${\displaystyle ({\mathcal {A}}B)(\psi )=\ (\forall \phi :\phi _{0}=\psi \to B(\phi ))}$	Tout : φ doit tenir sur tous les chemins à partir de l'état actuel.
E φ	${\displaystyle \exists \phi }$	${\displaystyle ({\mathcal {E}}B)(\psi )=\ (\exists \phi :\phi _{0}=\psi \land B(\phi ))}$	E xists: il existe au moins un chemin partant de l'état actuel où φ cales.

Symboles alternatifs :

• l'opérateur R est parfois noté V
• L'opérateur W est l' opérateur faible jusqu'à ce que : équivaut à${\displaystyle f\mathbf {W} g}$${\displaystyle f\mathbf {U} g\lor \mathbf {G} f}$

Les opérateurs unaires sont des formules bien formées lorsque B( φ ) est bien formé. Les opérateurs binaires sont des formules bien formées lorsque B( φ ) et C( φ ) sont bien formés.

Dans certaines logiques, certains opérateurs ne peuvent pas être exprimés. Par exemple, l' opérateur N ne peut pas être exprimé en logique temporelle d'actions .

Logiques temporelles

Les logiques temporelles incluent :

• Quelques systèmes de logique positionnelle
• Logique temporelle d'intervalle (ITL)
• Logique temporelle linéaire (LTL)
• Logique d'arbre de calcul (CTL)
• Logique temporelle du signal (STL)
• Logique temporelle d'horodatage (TTL)
• Langage de spécification de propriété (PSL)
• CTL* qui généralise LTL et CTL
• Logique Hennessy-Milner (HML)
• -calcul modal qui inclut comme sous-ensemble HML et CTL*
• Logique temporelle métrique (MTL)
• Logique temporelle d'intervalle métrique (MITL)
• Logique temporelle propositionnelle temporisée (TPTL)
• Logique temporelle linéaire tronquée (TLTL)
• Logique hyper temporelle (HyperLTL)

Une variation, étroitement liée aux logiques temporelles ou chronologiques ou tendues, sont des logiques modales basées sur la « topologie », le « lieu » ou la « position spatiale ».

Voir également

• Formalisme HPO
• Structure de Kripke
• Théorie des automates
• Grammaire de Chomsky
• Système de transition étatique
• Calcul de la durée (DC)
• Logique hybride
• Logique temporelle dans la vérification des états finis
• Logique temporelle des actions (TLA)
• Publications importantes en vérification formelle (y compris l'utilisation de la logique temporelle en vérification formelle )
• Langue de coordination Reo
• Logique modale
• Documents de recherche : Archives de la société Max Planck

Remarques

Les références

• Mordechai Ben-Ari, Zohar Manna, Amir Pnueli : La logique temporelle du temps de branchement . POPL 1981 : 164-176
• Amir Pnueli : La logique temporelle des programmes FOCS 1977 : 46-57
• Venema, Yde, 2001, "Temporal Logic", dans Goble, Lou, éd., The Blackwell Guide to Philosophical Logic . Blackwell.
• EA Emerson et C. Lei, « Modalités de vérification de modèle : la logique du temps de branchement contre-attaque », dans Science of Computer Programming 8, pp. 275-306, 1987.
• EA Emerson, " Logique temporelle et modale ", Handbook of Theoretical Computer Science , chapitre 16, the MIT Press, 1990
• Une introduction pratique à PSL , Cindy Eisner, Dana Fisman
• Vardi, Moshé Y. (2008). « De l' Église et du Prieur à PSL ». à Orna Grumberg ; Helmut Veith (éd.). 25 ans de model-checking : historique, réalisations, perspectives . Springer. ISBN 978-3-540-69849-4. préimpression . Perspective historique sur la façon dont des idées apparemment disparates se sont réunies en informatique et en ingénierie. (La mention de Church dans le titre de cet article est une référence à un article peu connu de 1957, dans lequel Church proposait un moyen d'effectuer la vérification du matériel.)

Lectures complémentaires

• Peter Øhrstrm; Par FV Hasle (1995). Logique temporelle : des idées anciennes à l'intelligence artificielle . Springer. ISBN 978-0-7923-3586-3.

Liens externes

• Stanford Encyclopedia of Philosophy : " Temporal Logic "—par Anthony Galton.
• Logique temporelle d'Yde Venema, description formelle de la syntaxe et de la sémantique, questions d'axiomatisation. Traiter aussi les opérateurs temporels dyadiques de Kamp (depuis, jusqu'à)
• Notes sur les jeux en logique temporelle par Ian Hodkinson, y compris une description formelle de la logique temporelle du premier ordre
• CADP - fournit des vérificateurs de modèles génériques pour diverses logiques temporelles
• PAT est un puissant vérificateur de modèle gratuit, un vérificateur LTL, un simulateur et un vérificateur de raffinement pour CSP et ses extensions (avec variable partagée, tableaux, large gamme d'équité).