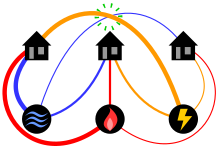
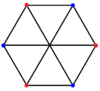
Problème de trois utilitaires - Three utilities problem

"Eau, gaz et électricité" redirige ici. Pour les utilitaires, voir Service public .
Le problème des trois utilitaires. Chaque maison peut-elle être connectée à chaque service public, sans qu'aucune ligne de connexion ne se croise?
Dans un avion, une traversée est nécessaire

Le puzzle mathématique classique connu sous le nom de problème des trois utilitaires ; le problème des trois chalets ou parfois de l' eau, du gaz et de l'électricité peut être énoncé comme suit:

Supposons qu'il y ait trois chalets sur un plan (ou une sphère) et que chacun doive être connecté aux compagnies d'eau, de gaz et d'électricité. Sans utiliser une troisième dimension ou envoyer aucune des connexions via une autre entreprise ou un autre chalet, y a-t-il un moyen de faire les neuf connexions sans qu'aucune des lignes ne se croise?

Le problème est un puzzle mathématique abstrait qui impose des contraintes qui n'existeraient pas dans une situation d'ingénierie pratique. Il fait partie du domaine mathématique de la théorie des graphes topologiques qui étudie l' incorporation de graphes sur des surfaces . En termes plus formels de théorie des graphes , le problème demande si le graphe biparti complet K 3,3 est planaire . Ce graphique est souvent appelé graphique d'utilité en référence au problème; il a également été appelé le graphe de Thomsen .

Histoire

Une revue de l'histoire du problème des trois utilités est donnée par Kullman (1979) . Il déclare que la plupart des références publiées au problème le qualifient de "très ancien". Dans la première publication trouvée par Kullman, Henry Dudeney  ( 1917 ) le nomme «eau, gaz et électricité». Cependant, Dudeney affirme que le problème est "aussi vieux que les collines ... beaucoup plus ancien que l'éclairage électrique , ou même le gaz ". Dudeney a également publié le même puzzle précédemment, dans The Strand Magazine en 1913.

Une autre version précoce du problème consiste à connecter trois maisons à trois puits. Il est énoncé de manière similaire à un casse-tête différent (et résoluble) qui implique également trois maisons et trois fontaines, les trois fontaines et une maison touchant un mur rectangulaire; le casse-tête consiste encore une fois à établir des connexions non croisées, mais seulement entre trois paires désignées de maisons et de puits ou de fontaines, comme dans les puzzles de liaison numériques modernes .

Mathématiquement, le problème peut être formulé en termes de dessins graphique du graphe biparti complet K 3,3 . Ce graphique fait une première apparition dans Henneberg (1908) . Il a six sommets, divisés en deux sous-ensembles de trois sommets et neuf arêtes, une pour chacune des neuf façons d'apparier un sommet d'un sous-ensemble avec un sommet de l'autre sous-ensemble. Le problème des trois utilitaires est la question de savoir si ce graphe est un graphe planaire .

Solution

Le graphe d'utilité, également connu sous le nom de graphe de Thomsen ou K 3,3
Preuve sans mots : une maison est temporairement supprimée. Les lignes reliant les maisons restantes aux services publics divisent le plan en trois régions, ombrées en jaune, rouge et bleu. Quelle que soit la région dans laquelle la maison supprimée est placée, l'utilitaire de couleur similaire se trouve en dehors de la région. Le théorème de la courbe de Jordan stipule qu'une ligne qui les relie doit intersecter l'une des lignes existantes.

Comme il est généralement présenté (sur un plan plat bidimensionnel), la solution au casse-tête utilitaire est «non»: il n'y a aucun moyen de faire les neuf connexions sans qu'aucune des lignes ne se croisent. En d'autres termes, le graphe K 3,3 n'est pas plan. Kazimierz Kuratowski a déclaré en 1930 que K 3,3 est non planaire, d'où il résulte que le problème n'a pas de solution. Kullman, cependant, déclare que "Il est intéressant de noter que Kuratowski n'a pas publié de preuve détaillée que [ K 3,3 est] non planaire".

Une preuve de l'impossibilité de trouver un plongement planaire de K 3,3 utilise une analyse de cas impliquant le théorème de la courbe de Jordan . Dans cette solution, on examine différentes possibilités pour les emplacements des sommets par rapport aux 4 cycles du graphe et montre qu'ils sont tous incompatibles avec un plongement planaire.

Alternativement, il est possible de montrer que tout graphe plan bipartite sans pont avec des sommets V et des arêtes E a E ≤ 2 V - 4 en combinant la formule d'Euler V - E + F = 2 (où F est le nombre de faces d'un plongement planaire ) avec l'observation que le nombre de faces est au plus égal à la moitié du nombre d'arêtes (les sommets autour de chaque face doivent alterner entre les maisons et les services publics, de sorte que chaque face a au moins quatre arêtes, et chaque arête appartient à exactement deux faces). Dans le graphe d'utilité, E  = 9 et 2 V  - 4 = 8 , violant cette inégalité, de sorte que le graphe d'utilité ne peut pas être planaire.

Généralisations

K 3,3 tiré avec un seul croisement.
Solution au problème des trois utilitaires sur un tore.

Deux caractérisations importantes des graphes planaires, le théorème de Kuratowski selon lequel les graphes planaires sont exactement les graphes qui ne contiennent ni K 3,3 ni le graphe complet K 5 comme subdivision, et le théorème de Wagner selon lequel les graphes planaires sont exactement les graphes qui ne contiennent ni K 3 , 3 ni K 5 en tant que mineur , utilisent et généralisent la non-planéité de K 3,3 .

K 3,3 est un graphe toroïdal , ce qui signifie qu'il peut être intégré sans croisements sur un tore . En ce qui concerne le problème des trois chalets, cela signifie que le problème peut être résolu en perforant deux trous à travers le plan (ou la sphère) et en les reliant avec un tube. Cela modifie les propriétés topologiques de la surface et l'utilisation du tube permet de relier les trois chalets sans croisement de lignes. Une déclaration équivalente est que le genre de graphe du graphe d'utilité est un, et par conséquent, il ne peut pas être incorporé dans une surface de genre inférieur à un. Une surface de genre un équivaut à un tore. Un encastrement toroïdal de K 3,3 peut être obtenu en remplaçant le croisement par un tube, comme décrit ci-dessus, dans lequel les deux trous où le tube se connecte au plan sont placés le long d'un des bords de croisement de part et d'autre du croisement. Une autre façon de changer les règles du puzzle est de permettre aux lignes de service public de passer à travers les chalets ou les services publics; cette liberté supplémentaire permet de résoudre le casse-tête.

Le " problème de la fabrique de briques " de Pál Turán demande plus généralement une formule pour le nombre minimum de croisements dans un dessin du graphe biparti complet K a , b en termes des nombres de sommets a et b des deux côtés de la bipartition . Le graphe d'utilité K 3,3 peut être tracé avec un seul croisement, mais pas avec des passages par zéro, son numéro de passage est donc un.

Autres propriétés de la théorie des graphes

Le graphe d'utilité K 3,3 est un graphe circulant . C'est la cage (3,4) , le plus petit graphique cubique sans triangle . Comme tous les autres graphes bipartis complets , il s'agit d'un graphe bien couvert , ce qui signifie que chaque ensemble indépendant maximal a la même taille. Dans ce graphique, les deux seuls ensembles indépendants maximaux sont les deux côtés de la bipartition, et ils sont évidemment égaux. K 3,3 est l'un des sept graphes bien couverts 3-réguliers 3-connectés .

C'est aussi un graphe de Laman , ce qui signifie qu'il forme un système minimalement rigide lorsqu'il est intégré (avec des croisements) dans le plan. C'est le plus petit exemple de graphe de Laman non planaire, car l'autre graphe non planaire minimal, K 5 , n'est pas minimalement rigide.

Les références

Liens externes