Diplôme de Turing - Turing degree

En informatique et en logique mathématique, le degré de Turing (du nom d' Alan Turing ) ou degré d'insolvabilité d'un ensemble de nombres naturels mesure le niveau d'insolvabilité algorithmique de l'ensemble.

Aperçu

Le concept de degré de Turing est fondamental dans la théorie de la calculabilité , où les ensembles de nombres naturels sont souvent considérés comme des problèmes de décision . Le degré de Turing d'un ensemble est une mesure de la difficulté de résoudre le problème de décision associé à l'ensemble, c'est-à-dire de déterminer si un nombre arbitraire se trouve dans l'ensemble donné.

Deux ensembles sont équivalents de Turing s'ils ont le même niveau d'insolvabilité ; chaque degré de Turing est une collection d'ensembles équivalents de Turing, de sorte que deux ensembles sont dans des degrés de Turing différents exactement quand ils ne sont pas équivalents à Turing. De plus, les degrés de Turing sont partiellement ordonnés de sorte que si le degré de Turing d'un ensemble X est inférieur au degré de Turing d'un ensemble Y, alors toute procédure (non calculable) qui décide correctement si les nombres sont dans Y peut être effectivement convertie en une procédure qui décide correctement si les nombres sont dans X . C'est en ce sens que le degré de Turing d'un ensemble correspond à son niveau d'insolvabilité algorithmique.

Les degrés Turing ont été introduits par Emil Leon Post (1944), et de nombreux résultats fondamentaux ont été établis par Stephen Cole Kleene et Post (1954). Les diplômes de Turing ont été un domaine de recherche intense depuis lors. De nombreuses preuves dans le domaine utilisent une technique de preuve connue sous le nom de méthode de priorité .

Équivalence de Turing

Pour la suite de cet article, le mot ensemble fera référence à un ensemble de nombres naturels. Un ensemble X est dit Turing réductible à un ensemble Y s'il existe une machine oracle de Turing qui décide de l'appartenance à X lorsqu'on lui donne un oracle pour l'appartenance à Y . La notation X ≤ _T Y indique que X est Turing réductible à Y .

Deux ensembles X et Y sont définis comme Turing équivalents si X est Turing réductible à Y et Y est Turing réductible à X . La notation X ≡ _T Y indique que X et Y sont Turing équivalent. La relation ≡ _T peut être considérée comme une relation d'équivalence , ce qui signifie que pour tous les ensembles X , Y et Z :

• X ≡ _T X
• X ≡ _T Y implique Y ≡ _T X
• Si X ≡ _T Y et Y ≡ _T Z puis X ≡ _T Z .

Un degré de Turing est une classe d'équivalence de la relation ≡ _T . La notation [ X ] désigne la classe d'équivalence contenant un ensemble X . L'ensemble des degrés de Turing est noté . ${\displaystyle {\mathcal {D}}}$

Les degrés de Turing ont un ordre partiel ≤ défini de telle sorte que [ X ] ≤ [ Y ] si et seulement si X ≤ _T Y . Il existe un degré de Turing unique contenant tous les ensembles calculables, et ce degré est inférieur à tous les autres degrés. Il est noté 0 (zéro) car c'est le moindre élément du poset . (Il est courant d'utiliser la notation en gras pour les degrés de Turing, afin de les distinguer des ensembles. Lorsqu'aucune confusion ne peut se produire, comme avec [ X ], la mise en gras n'est pas nécessaire.) ${\displaystyle {\mathcal {D}}}$

Pour tous les jeux X et Y , X rejoignent Y, écrit X ⊕ Y , est défini comme l'union des ensembles {2 n  : n ∈ X } et {2 m +1: m ∈ Y }. Le degré de Turing X ⊕ Y est la borne supérieure des degrés de X et Y . Ainsi est une jointure-semi-treillis . La borne supérieure des degrés a et b est notée a ∪ b . On sait que ce n'est pas un treillis , car il existe des paires de degrés sans plus grande borne inférieure. ${\displaystyle {\mathcal {D}}}$${\displaystyle {\mathcal {D}}}$

Pour tout ensemble X, la notation X ′ désigne l'ensemble des indices des machines oracle qui s'arrêtent (lorsqu'on leur donne leur indice en entrée) lors de l'utilisation de X comme oracle. L'ensemble X est appelé le saut de Turing de X . Le saut de Turing d'un degré [ X ] est défini comme étant le degré [ X ′] ; c'est une définition valable parce que X '≡ _T Y ' lorsque X ≡ _T Y . Un exemple clé est 0 , le degré du problème d'arrêt .

Propriétés de base des degrés de Turing

• Chaque degré de Turing est dénombrable infini , c'est-à-dire qu'il contient exactement des ensembles.${\displaystyle \aleph _{0}}$
• Il existe des degrés de Turing distincts.${\displaystyle 2^{\aleph _{0}}}$
• Pour chaque degré a, l'inégalité stricte a < a est vérifiée.
• Pour chaque degré a , l'ensemble des degrés inférieurs à a est dénombrable . L'ensemble des degrés supérieurs à a a une taille .${\displaystyle 2^{\aleph _{0}}}$

Structure des diplômes de Turing

De nombreuses recherches ont été menées sur la structure des diplômes de Turing. L'enquête suivante ne répertorie que quelques-uns des nombreux résultats connus. Une conclusion générale qui peut être tirée de la recherche est que la structure des degrés Turing est extrêmement compliquée.

Propriétés de la commande

• Il existe des diplômes minimaux . Un degré a est minimal si a est différent de zéro et qu'il n'y a pas de degré entre 0 et a . Ainsi la relation d'ordre sur les degrés n'est pas un ordre dense .
• Pour chaque degré non nul d' un il y a un degré b incomparable avec un .
• Il existe un ensemble de degrés de Turing incomparables par paires.${\displaystyle 2^{\aleph _{0}}}$
• Il existe des paires de degrés sans plus grande borne inférieure. Ce n'est donc pas un treillis.${\displaystyle {\mathcal {D}}}$
• Chaque ensemble dénombrable partiellement ordonné peut être intégré dans les degrés de Turing.
• Aucune séquence infinie et strictement croissante de degrés n'a de borne supérieure.

Propriétés impliquant le saut

• Pour chaque degré a, il existe un degré strictement compris entre a et a′ . En fait, il existe une famille dénombrable de degrés incomparables deux à deux entre a et a′ .
• Inversion de saut : un degré a est de la forme b′ si et seulement si 0′ ≤ a .
• Pour tout degré a il existe un degré b tel que a < b et b′ = a′ ; un tel degré b est dit faible par rapport à a .
• Il y a une séquence infinie a _i de degrés de telle sorte que la ' _{i 1} ≤ a _i pour chaque i .

Propriétés logiques

• Simpson (1977) a montré que la théorie du premier ordre de dans le langage ⟨ ≤, = ⟩ ou ⟨ ≤, ′, = est plusieurs-un équivalente à la théorie de l' arithmétique vraie du second ordre . Cela indique que la structure de est extrêmement compliquée.${\displaystyle {\mathcal {D}}}$${\displaystyle {\mathcal {D}}}$
• Shore et Slaman (1999) ont montré que l'opérateur de saut est définissable dans la structure du premier ordre de avec le langage ⟨ ≤, = ⟩ .${\displaystyle {\mathcal {D}}}$

Degrés de Turing énumérables récursivement

Un réseau fini qui ne peut pas être intégré dans les degrés re.

Un degré est appelé récursivement énumérable (re) s'il contient un ensemble récursivement énumérable . Chaque degré ré est inférieur à 0′ , mais tous les degrés inférieurs à 0′ ne sont pas ré.

• ( GE Sacks , 1964) Les degrés ré sont denses ; entre deux degrés de ré, il y a un troisième degré de ré.
• (AH Lachlan, 1966a et CEM Yates, 1966) Il y a deux degrés re sans plus grande limite inférieure dans les degrés re.
• (AH Lachlan, 1966a et CEM Yates, 1966) Il existe une paire de degrés non nuls dont la plus grande borne inférieure est 0 .
• (AH Lachlan, 1966b) Il n'y a pas de paire de degrés re dont la plus grande borne inférieure est 0 et dont la plus petite borne supérieure est 0′ . Ce résultat est appelé officieusement le théorème du non- diamant .
• (SK Thomason, 1971) Tout réseau distributif fini peut être intégré dans les degrés re. En fait, l' algèbre booléenne sans atome dénombrable peut être intégrée de manière à préserver suprema et infima .
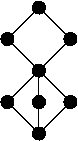
• (AH Lachlan et RI Soare , 1980) Tous les réseaux finis ne peuvent pas être intégrés dans les degrés re (via un intégration qui préserve suprema et infima). Un exemple particulier est montré à droite.
• ( LA Harrington et TA Slaman , voir Nies, Shore et Slaman (1998)) Le premier ordre théorie des degrés re dans la langue ⟨ 0 , ≤, =⟩ est beaucoup-un équivalent à la théorie du vrai premier ordre arithmétique .

Problème de poste et méthode de priorité

Emil Post a étudié les degrés de re Turing et a demandé s'il y avait un degré de re strictement compris entre 0 et 0′ . Le problème de construire un tel degré (ou de montrer qu'il n'en existe pas) est devenu connu sous le nom de problème de Post . Ce problème a été résolu de manière indépendante par Friedberg et Muchnik dans les années 1950, qui ont montré que ces degrés intermédiaires existent bel et bien. Leurs preuves développaient chacune la même nouvelle méthode de construction des re degrés, connue sous le nom de méthode prioritaire . La méthode de priorité est maintenant la principale technique pour établir des résultats sur les réinitialisations.

L'idée de la méthode de priorité pour construire une réinitialisation X est de lister une séquence dénombrable d' exigences que X doit satisfaire. Par exemple, pour construire une réinitialisation X comprise entre 0 et 0′ il suffit de satisfaire les exigences A _e et B _e pour chaque entier naturel e , où A _e requiert que la machine oracle d'indice e ne calcule pas 0′ à partir de X et B _e exige que la machine de Turing d'indice e (et sans oracle) ne calcule pas X . Ces exigences sont placées dans un ordre de priorité , qui est une bijection explicite des exigences et des nombres naturels. La preuve procède de manière inductive avec une étape pour chaque entier naturel ; ces étapes peuvent être considérées comme des pas de temps pendant lesquels l'ensemble X est énuméré. À chaque étape, les nombres peuvent être mis dans X ou empêchés à jamais d'entrer dans X pour tenter de satisfaire les exigences (c'est-à-dire les forcer à tenir une fois que tout X a été énuméré). Parfois, un nombre peut être énuméré dans X pour satisfaire une exigence, mais cela entraînerait l'insatisfaction d'une exigence précédemment satisfaite (c'est-à-dire qu'elle serait blessée ). L'ordre de priorité des exigences est utilisé pour déterminer quelle exigence satisfaire dans ce cas. L'idée informelle est que si une exigence est endommagée, elle cessera finalement d'être endommagée une fois que toutes les exigences de priorité plus élevée auront cessé d'être endommagées, bien que tous les arguments de priorité n'aient pas cette propriété. Il faut argumenter que l'ensemble X est ré et satisfait à toutes les exigences. Les arguments de priorité peuvent être utilisés pour prouver de nombreux faits sur les réinitialisations ; les exigences utilisées et la manière dont elles sont satisfaites doivent être soigneusement choisies pour produire le résultat requis.

Voir également

• Martin mesure

Les références

Monographies (niveau licence)

• Cooper, SB Théorie de la calculabilité . Chapman & Hall/CRC, Boca Raton, Floride, 2004. ISBN  1-58488-237-9
• Cutland, N. Calculabilité . Cambridge University Press, Cambridge-New York, 1980. ISBN  0-521-22384-9 ; ISBN  0-521-29465-7

Monographies et articles de sondage (niveau universitaire)

• Ambos-Spies, K. et Fejer, P. Degrés d'insolvabilité. Inédit. http://www.cs.umb.edu/~fejer/articles/History_of_Degrees.pdf
• Lerman, M. Degrés d'insolvabilité. Perspectives en logique mathématique. Springer-Verlag, Berlin, 1983. ISBN  3-540-12155-2
• Odifreddi, PG (1989), Théorie de la récursion classique , Études en logique et fondements des mathématiques, 125 , Amsterdam: North-Holland, ISBN 978-0-444-87295-1, MR  0982269
• Odifreddi, PG (1999), Théorie de la récursion classique. Vol. II , Studies in Logic and the Foundations of Mathematics, 143 , Amsterdam: North-Holland, ISBN 978-0-444-50205-6, MR  1718169
• Rogers, H. La théorie des fonctions récursives et la calculabilité efficace , MIT Press. ISBN  0-262-68052-1 , ISBN  0-07-053522-1
• Sacks, Gerald E. Degrees of Unsolvability (Annals of Mathematics Studies), Princeton University Press. ISBN  978-0-6910-7941-7
• Simpson, S. Degrés d'insolvabilité : une enquête sur les résultats. Handbook of Mathematical Logic , North-Holland, 1977, pp. 631–652.
• Shoenfield, Joseph R. Degrés d'insolvabilité , Hollande du Nord/Elsevier, ISBN  978-0-7204-2061-6 .
• Shore, R. (1993). « Les théories des degrés T, tt et wtt re : indécidabilité et au-delà ». Dans Univ. Nac. del Sur, Bahía Blanca (éd.). Actes du IXe Symposium latino-américain sur la logique mathématique, partie 1 (Bahía Blanca, 1992) . Notas Logica Mat. 38 . p. 61-70.
• Soare, R. Ensembles et degrés récursivement énumérables. Perspectives en logique mathématique. Springer-Verlag, Berlin, 1987. ISBN  3-540-15299-7
• Soare, Robert I. Ensembles et degrés récursivement énumérables. Taureau. Amer. Math. Soc. 84 (1978), n. 6, 1149-1181. MR 508451

Documents de recherche

• Kleene, Stephen Cole ; Post, Emil L. (1954), "Le semi-réseau supérieur des degrés d'insolvabilité récursive", Annals of Mathematics , Second Series, 59 (3) : 379–407, doi : 10.2307/1969708 , ISSN  0003-486X , JSTOR  1969708 , MR  0061078
• Lachlan, AH (1966a), "Lower Bounds for Pairs of Recursively Enumerable Degrees", Actes de la London Mathematical Society , 3 (1) : 537-569, CiteSeerX  10.1.1.106.7893 , doi : 10.1112/plms/s3-16.1 .537 .
• Lachlan, AH (1966b), "L'impossibilité de trouver des compléments relatifs pour les degrés récursivement énumérables", J. Symb. Enregistrer. , 31 (3) : 434–454, doi : 10.2307/2270459 , JSTOR  2270459 .
• Lachlan, AH ; Soare, RI (1980), "Pas tous les treillis finis sont intégrables dans les degrés récursivement énumérables", Advances in Mathematics , 37 : 78-82, doi : 10.1016/0001-8708(80)90027-4 .
• Nies, André; Rive, Richard A.; Slaman, Theodore A. (1998), "Interpretability and definability in the recursively enumerable degree", Actes de la London Mathematical Society , 77 (2) : 241-291, CiteSeerX  10.1.1.29.9588 , doi : 10.1112/S002461159800046X , ISSN  0024-6115 , MR  1635141
• Post, Emil L. (1944), "Ensembles récursivement énumérables d'entiers positifs et leurs problèmes de décision", Bulletin de l'American Mathematical Society , 50 (5) : 284-316, doi : 10.1090/S0002-9904-1944-08111- 1 , ISSN  0002-9904 , MR  0010514
• Sacks, GE (1964), "Les degrés récursivement énumérables sont denses", Annals of Mathematics , Second Series, 80 (2) : 300-312, doi : 10.2307/1970393 , JSTOR  1970393 .
• Rive, Richard A. ; Slaman, Theodore A. (1999), "Defining the Turing jump", Mathematical Research Letters , 6 (6): 711-722, doi : 10.4310/mrl.1999.v6.n6.a10 , ISSN  1073-2780 , MR  1739227
• Simpson, Stephen G. (1977), "Théorie du premier ordre des degrés d'insolvabilité récursive", Annals of Mathematics , Second Series, 105 (1) : 121–139, doi : 10.2307/1971028 , ISSN  0003-486X , JSTOR  19711028 , MR  0432435
• Thomason, SK (1971), "Sous-réseaux des degrés récursivement énumérables", Z. Math. Logik Grundlag. Math. , 17 : 273–280, doi : 10.1002/malq.19710170131 .
• Yates, CEM (1966), « A minimal pair of recursively enumerable degree », Journal of Symbolic Logic , 31 (2) : 159-168, doi : 10.2307/2269807 , JSTOR  2269807 .