Arbre binaire sans racine - Unrooted binary tree

Un cladogramme sous la forme d'un arbre binaire non raciné, représentant les similitudes et l'histoire de l'évolution entre les espèces d' actinobactéries .

En mathématiques et en informatique, un arbre binaire non enraciné est un arbre non enraciné dans lequel chaque sommet a un ou trois voisins.

Définitions

Un arbre libre ou un arbre non enraciné est un graphe non orienté connecté sans cycles . Les sommets avec un voisin sont les feuilles de l'arbre, et les sommets restants sont les nœuds internes de l'arbre. Le degré d'un sommet est son nombre de voisins ; dans un arbre à plusieurs nœuds, les feuilles sont les sommets de degré un. Un arbre binaire non enraciné est un arbre libre dans lequel tous les nœuds internes ont exactement le degré trois.

Dans certaines applications, il peut être judicieux de distinguer les sous-types d'arbres binaires non enracinés : un plongement planaire de l'arbre peut être fixé en spécifiant un ordre cyclique pour les arêtes à chaque sommet, ce qui en fait un arbre plan . En informatique, les arbres binaires sont souvent enracinés et ordonnés lorsqu'ils sont utilisés comme structures de données , mais dans les applications d'arbres binaires non enracinés dans le regroupement hiérarchique et la reconstruction d' arbres évolutifs , les arbres non ordonnés sont plus courants.

De plus, on peut distinguer les arbres dans lesquels tous les sommets ont des étiquettes distinctes, les arbres dans lesquels seules les feuilles sont étiquetées et les arbres dans lesquels les nœuds ne sont pas étiquetés. Dans un arbre binaire non enraciné avec n feuilles, il y aura n  − 2 nœuds internes, donc les étiquettes peuvent être tirées de l'ensemble des entiers de 1 à 2 n  − 1 lorsque tous les nœuds doivent être étiquetés, ou de l'ensemble des entiers de 1 à n lorsque seules les feuilles doivent être étiquetées.

Structures associées

Arbres binaires enracinés

Un arbre binaire non enraciné T peut être transformé en un arbre binaire entièrement enraciné (c'est-à-dire un arbre enraciné dans lequel chaque nœud non-feuille a exactement deux enfants) en choisissant une arête racine e de T , en plaçant un nouveau nœud racine au milieu de e et en éloignant chaque arête de l'arbre subdivisé résultant du nœud racine. Inversement, tout arbre binaire à racine complète peut être transformé en un arbre binaire sans racine en supprimant le nœud racine, en remplaçant le chemin entre ses deux enfants par une seule arête non dirigée et en supprimant l'orientation des arêtes restantes dans le graphe. Pour cette raison, il y a exactement 2 n  -3 fois plus d'arbres binaires à racines complètes avec n feuilles qu'il y a d'arbres binaires non racinés avec n feuilles.

Classification hiérarchique

Un regroupement hiérarchique d'une collection d'objets peut être formalisé comme une famille maximale d'ensembles d'objets dans lesquels deux ensembles ne se croisent pas. C'est-à-dire que pour deux ensembles S et T dans la famille, soit S et T sont disjoints, soit l'un est un sous-ensemble de l'autre, et aucun autre ensemble ne peut être ajouté à la famille tout en préservant cette propriété. Si T est un arbre binaire non enraciné, il définit un regroupement hiérarchique de ses feuilles : pour chaque arête ( u , v ) de T il existe un cluster constitué des feuilles qui sont plus proches de u que de v , et ces ensembles avec le l'ensemble vide et l'ensemble de toutes les feuilles forment une famille maximale non croisée. Inversement, à partir de n'importe quelle famille d'ensembles maximale non-croisée sur un ensemble de n éléments, on peut former un unique arbre binaire non enraciné qui a un nœud pour chaque triple ( A , B , C ) d'ensembles disjoints dans la famille qui couvrent ensemble tous des éléments.

Arbres évolutifs

Selon des formes simples de la théorie de l'évolution , l'histoire de la vie peut être résumée comme un arbre phylogénétique dans lequel chaque nœud décrit une espèce, les feuilles représentent les espèces qui existent aujourd'hui et les bords représentent les relations ancêtres-descendants entre espèces. Cet arbre a une orientation naturelle d'ancêtres en descendants, et une racine chez l' ancêtre commun de l'espèce, c'est donc un arbre enraciné. Cependant, certaines méthodes de reconstruction d'arbres binaires ne peuvent reconstruire que les nœuds et les arêtes de cet arbre, mais pas leurs orientations.

Par exemple, les méthodes cladistiques telles que la parcimonie maximale utilisent comme données un ensemble d'attributs binaires décrivant les caractéristiques de l'espèce. Ces méthodes recherchent un arbre avec l'espèce donnée en tant que feuilles dans lesquelles les nœuds internes sont également étiquetés avec des caractéristiques, et tentent de minimiser le nombre de fois qu'une caractéristique est présente à un seul des deux points d'extrémité d'une arête de l'arbre. Idéalement, chaque caractéristique ne devrait avoir qu'un seul bord pour lequel c'est le cas. Changer la racine d'un arbre ne change pas ce nombre de différences d'arêtes, donc les méthodes basées sur la parcimonie ne sont pas capables de déterminer l'emplacement de la racine de l'arbre et produiront un arbre non enraciné, souvent un arbre binaire non enraciné.

Les arbres binaires non racinés sont également produits par des méthodes pour déduire des arbres évolutifs basés sur des données de quatuor spécifiant, pour chaque espèce de quatre feuilles, l'arbre binaire non raciné décrivant l'évolution de ces quatre espèces, et par des méthodes qui utilisent la distance de quatuor pour mesurer la distance entre les arbres.

Décomposition de branches

Les arbres binaires non enracinés sont également utilisés pour définir des décompositions de branches de graphes, en formant un arbre binaire non enraciné dont les feuilles représentent les arêtes du graphe donné. C'est-à-dire qu'une décomposition en branches peut être considérée comme un regroupement hiérarchique des bords du graphe. Les décompositions de branches et une quantité numérique associée, la largeur de branche, sont étroitement liées à la largeur d' arbre et constituent la base d' algorithmes de programmation dynamique efficaces sur les graphes.

Énumération

En raison de leurs applications en clustering hiérarchique, le problème d' énumération de graphes le plus naturel sur les arbres binaires non enracinés est de compter le nombre d'arbres avec n feuilles étiquetées et nœuds internes non étiquetés. Un arbre binaire non enraciné sur n feuilles étiquetées peut être formé en connectant la n ième feuille à un nouveau nœud au milieu de l'un des bords d'un arbre binaire non enraciné sur n  − 1 feuilles étiquetées. Il y a 2 n  − 5 arêtes auxquelles le n ième nœud peut être attaché ; par conséquent, le nombre d'arbres sur n feuilles est plus grand que le nombre d'arbres sur n  − 1 feuilles d'un facteur de 2 n  − 5. Ainsi, le nombre d'arbres sur n feuilles étiquetées est la double factorielle

${\displaystyle (2n-5)!!={\frac {(2n-4)!}{(n-2)!2^{n-2}}}.}$

Les nombres d'arbres sur 2, 3, 4, 5, ... feuilles étiquetées sont

1, 1, 3, 15, 105, 945, 10395, 135135, 2027025, 34459425, ... (séquence A001147 dans l' OEIS ).

Égalités fondamentales

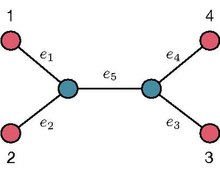
La longueur de chemin feuille à feuille sur un arbre binaire sans racine (UBT) fixe T code le nombre d'arêtes appartenant au chemin unique dans T reliant une feuille donnée à une autre feuille. Par exemple, en se référant à l'UBT montré dans l'image de droite, la longueur de chemin entre les feuilles 1 et 2 est égale à 2 alors que la longueur de chemin entre les feuilles 1 et 3 est égale à 3. La longueur de chemin séquence d'une feuille donnée sur un UBT T fixe encode les longueurs des chemins de la feuille donnée à tous les autres. Par exemple, en se référant à l'UBT montré dans l'image de droite, la séquence de longueur de chemin de la feuille 1 est . L'ensemble de séquences de longueur de chemin associé aux feuilles de T est généralement appelé la collection de séquences de longueur de chemin de T. ${\style d'affichage p_{1,2}}$${\style d'affichage p_{1,3}}$${\style d'affichage p_{1}=(p_{1,2},p_{1,3},p_{1,4})=(2,3,3)}$

Un exemple d'arbre binaire non raciné à quatre feuilles

Daniele Catanzaro, Raffaele Pesenti et Laurence Wolsey ont montré que la collection de séquences de longueur de chemin codant pour un UBT donné avec n feuilles doit satisfaire des égalités spécifiques, à savoir

• ${\style d'affichage p_{i,i}=0}$ pour tous ${\style d'affichage i\dans [1,n]}$
• ${\style d'affichage p_{i,j}=p_{j,i}}$ pour tous ${\displaystyle i,j\in [1,n]:i\neq j}$
• ${\displaystyle p_{i,i}\leq p_{i,k}+p_{k,j}}$ pour tous ${\displaystyle i,j,k\in [1,n]:i\neq j\neq k}$
• ${\displaystyle \sum _{j=1}^{n}1/2^{p_{i,j}}=1/2}$pour tous (qui est une adaptation de l' inégalité de Kraft-McMillan )${\style d'affichage i\dans [1,n]}$
• ${\displaystyle \sum _{i=1}^{n}\sum _{j=1}^{n}p_{i,j}/2^{p_{i,j}}=2n-3}$, également appelée variété phylogénétique .

Ces égalités s'avèrent nécessaires et indépendantes pour qu'une collection de longueurs de chemin encode un UBT à n feuilles. On ne sait pas actuellement s'ils sont également suffisants.

Noms alternatifs

Arbres binaires non racinées ont également été appelés arbres binaires libres , arbres cubes , arbres ternaires et arbres ternaires sans racines ,. Cependant, le nom « arbre binaire libre » a également été appliqué aux arbres non enracinés qui peuvent avoir des nœuds de degré deux et aux arbres binaires enracinés avec des enfants non ordonnés, et le nom « arbre ternaire » est plus fréquemment utilisé pour désigner un arbre enraciné avec trois enfants par nœud .

Remarques

Les références

• Calvitie, DJ ; Bishop, Martin J.; Cannings, Christopher (2007), Handbook of Statistical Genetics , 1 (3e éd.), Wiley-Interscience, p. 502, ISBN 978-0-470-05830-5.
• Cilibrasi, Rudi ; Vitanyi, Paul MB (2006). « Une nouvelle heuristique d'arbre de quatuor pour le regroupement hiérarchique ». arXiv : cs/0606048 ..
• Czumaj, Artur; Gibbons, Alan (1996), "Le problème de Guthrie : nouvelles équivalences et réductions rapides", Theoretical Computer Science , 154 (1) : 3-22, doi : 10.1016/0304-3975(95)00126-3.
• Eppstein, David (2009), "Squarepants in a tree: Sum of subtree clustering and hyperbolic pants decomposition", ACM Transactions on Algorithms , 5 (3) : 1-24, arXiv : cs.CG/0604034 , doi : 10.1145/1541885.1541890 , S2CID  2434.
• Exoo, Geoffrey (1996), "Une méthode simple pour construire de petits graphiques cubiques de circonférences 14, 15 et 16" (PDF) , Electronic Journal of Combinatorics , 3 (1): R30, doi : 10.37236/1254.
• Furnas, George W. (1984), "The generation of random, binary unordered trees", Journal of Classification , 1 (1) : 187-233, doi : 10.1007/BF01890123 , S2CID  121121529.
• Harary, Franck ; Palmer, EM ; Robinson, RW (1992), "Compter les arbres binaires libres admettant une hauteur donnée" (PDF) , Journal of Combinatorics, Information, and System Sciences , 17 : 175-181.
• Hendy, Michael D.; Penny, David (1989), "Un cadre pour l'étude quantitative des arbres évolutifs", Biologie systématique , 38 (4): 297-309, doi : 10.2307/2992396 , JSTOR  2992396
• Przytycka, Teresa M.; Larmore, Lawrence L. (1994), "Le problème de l'arbre alphabétique optimal revisité", Proc. 21st International Colloquium on Automata, Languages ​​and Programming (ICALP '94) , Notes de cours en informatique, 820 , Springer-Verlag, pp. 251-262, doi : 10.1007/3-540-58201-0_73.
• Robertson, Neil ; Seymour, Paul D. (1991), "Graph minors. X. Obstructions to tree-decomposition", Journal of Combinatorial Theory , 52 (2) : 153-190, doi : 10.1016/0095-8956(91)90061-N.
• Saint-Jean, Katherine; Warnow, Tandy ; Moret, Bernard ME ; Vawterd, Lisa (2003), « Etude des performances des méthodes phylogénétiques : méthodes de quartet (non pondérées) et jointure par les voisins » (PDF) , Journal of Algorithms , 48 (1) : 173-193, doi : 10.1016/S0196-6774 (03 )00049-X , S2CID  5550338.