Arbelos - Arbelos

Un arbelos (région grise)

Sculpture Arbelos à Kaatsheuvel , Pays-Bas

En géométrie , un arbelos est une région plane délimitée par trois demi-cercles avec trois sommets tels que chaque coin de chaque demi-cercle est partagé avec l'un des autres (connectés), tous du même côté d'une ligne droite (la ligne de base ) qui contient leur diamètres .

La plus ancienne référence connue à cette figure se trouve dans le Livre des Lemmes d' Archimède , où certaines de ses propriétés mathématiques sont énoncées dans les Propositions 4 à 8. Le mot arbelos est le grec pour «couteau de cordonnier». La figure est étroitement liée à la chaîne Pappus .

Propriétés

Deux des demi-cercles sont nécessairement concaves, avec des diamètres arbitraires a et b ; le troisième demi-cercle est convexe , de diamètre a + b .

Quelques points particuliers sur les arbelos.

Surface

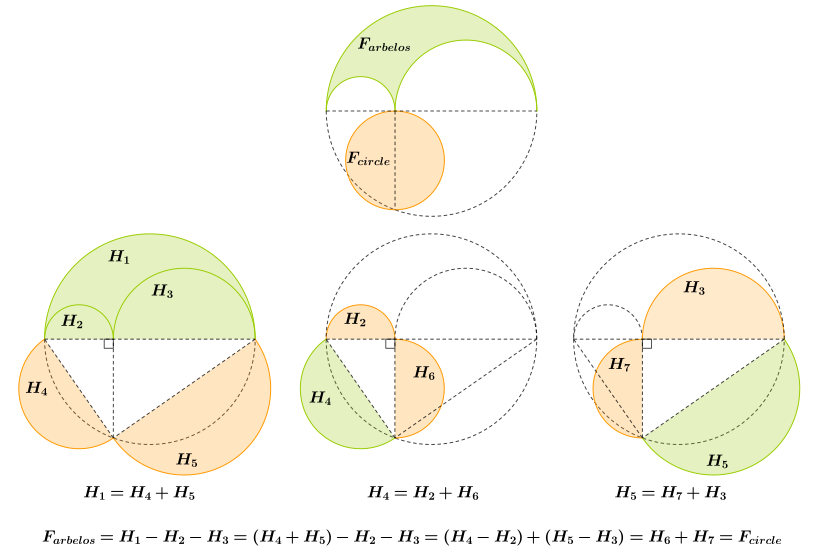
L' aire des arbelos est égale à l'aire d'un cercle de diamètre . ${\ displaystyle HA}$

Preuve : Pour la preuve, réfléchissez les arbelos sur la ligne passant par les points et , et observez que deux fois l'aire des arbelos est ce qui reste lorsque les aires des deux petits cercles (avec des diamètres ) sont soustraites de l'aire du grand cercle (avec diamètre ). Depuis l'aire d'un cercle est proportionnelle au carré du diamètre ( Euclide d » éléments , Livre XII, Proposition 2, nous ne savons pas besoin que la constante de proportionnalité est ), le problème se réduit à montrer que . La longueur est égale à la somme des longueurs et , donc cette équation se simplifie algébriquement à l'énoncé que . Ainsi, on prétend que la longueur du segment est la moyenne géométrique des longueurs des segments et . Or (voir Figure) le triangle , étant inscrit dans le demi-cercle, a un angle droit au point (Euclide, Livre III, Proposition 31), et par conséquent est bien une "moyenne proportionnelle" entre et (Euclide, Livre VI, Proposition 8 , Porisme). Cette preuve se rapproche de l'argument grec ancien; Harold P. Boas cite un article de Roger B. Nelsen qui a mis en œuvre l'idée comme la preuve suivante sans mots . ${\ displaystyle B}$ ${\ displaystyle C}$ ${\ displaystyle BA}$ ${\ displaystyle AC}$ ${\ displaystyle BC}$ ${\ displaystyle {\ frac {\ pi} {4}}}$ ${\ displaystyle 2 (AH) ^ {2} = (BC) ^ {2} - (AC) ^ {2} - (BA) ^ {2}}$ ${\ displaystyle (BC)}$ ${\ displaystyle (BA)}$ ${\ displaystyle (AC)}$ ${\ displaystyle (AH) ^ {2} = (BA) (AC)}$ ${\ displaystyle AH}$ ${\ displaystyle BA}$ ${\ displaystyle AC}$ ${\ displaystyle BHC}$ ${\ displaystyle H}$ ${\ displaystyle (HA)}$ ${\ displaystyle (BA)}$ ${\ displaystyle (AC)}$

Rectangle

Soit et soit les points où les segments et intersectent les demi - cercles et , respectivement. Le quadrilatère est en fait un rectangle . ${\ displaystyle D}$ ${\ displaystyle E}$ ${\ displaystyle BH}$ ${\ displaystyle CH}$ ${\ displaystyle AB}$ ${\ displaystyle AC}$ ${\ displaystyle ADHE}$

Preuve : Les angles , et sont des angles droits parce qu'ils sont inscrits dans des demi - cercles (par le théorème de Thalès ). Le quadrilatère a donc trois angles droits, c'est donc un rectangle. QED

{\ displaystyle BDA}

{\ displaystyle BHC}

{\ displaystyle AEC}

{\ displaystyle ADHE}

Tangentes

La ligne est tangente au demi-cercle à et demi-cercle à . ${\ displaystyle DE}$ ${\ displaystyle BA}$ ${\ displaystyle D}$ ${\ displaystyle AC}$ ${\ displaystyle E}$

Preuve : L'angle BDA étant un angle droit, l'angle DBA est égal à π / 2 moins l'angle DAB. Cependant, l'angle DAH est également égal à π / 2 moins l'angle DAB (puisque l'angle HAB est un angle droit). Par conséquent, les triangles DBA et DAH sont similaires . Par conséquent, l'angle DIA est égal à l'angle DOH, où I est le milieu de BA et O est le milieu de AH. Mais AOH est une ligne droite, donc l'angle DOH et DOA sont des angles supplémentaires . Par conséquent, la somme des angles DIA et DOA est π. L'angle IAO est un angle droit. La somme des angles dans n'importe quel quadrilatère est 2π, donc dans le quadrilatère IDOA, l'angle IDO doit être un angle droit. Mais ADHE est un rectangle, donc le milieu O de AH (la diagonale du rectangle) est aussi le milieu de DE (l'autre diagonale du rectangle). Comme I (défini comme le milieu de BA) est le centre du demi-cercle BA et que l'angle IDE est un angle droit, alors DE est tangent au demi-cercle BA en D. Par un raisonnement analogue DE est tangent au demi-cercle AC en E. QED

Les cercles d'Archimède

L'altitude divise les arbelos en deux régions, chacune délimitée par un demi-cercle, un segment de ligne droite et un arc du demi-cercle extérieur. Les cercles inscrits dans chacune de ces régions, appelés cercles d'Arbelos d' Archimède , ont la même taille. ${\ displaystyle AH}$

Variations et généralisations

exemple d'un f -belos

Le parbelos est une figure similaire aux arbelos, qui utilise des segments de parabole au lieu de demi-cercles. Une généralisation comprenant à la fois arbelos et parbelos est le f -belos, qui utilise un certain type de fonctions différentiables similaires.

Dans le modèle demi-plan de Poincaré du plan hyperbolique , un modèle de Arbelos un triangle idéal .

Étymologie

Le type de couteau de cordonnier qui a donné son nom à la figure

Le nom arbelos vient du grec ἡ ἄρβηλος he árbēlos ou ἄρβυλος árbylos , qui signifie «couteau de cordonnier», un couteau utilisé par les cordonniers de l'antiquité à nos jours, dont la lame ressemblerait à la figure géométrique.

Voir également

Les références

^ ^un ^b Weisstein, Eric W. "Arbelos" . MathWorld .
^ Thomas Little Heath (1897), Les œuvres d'Archimède . La presse de l'Universite de Cambridge. Proposition 4 dans le livre des lemmes . Citation: Si AB est le diamètre d'un demi-cercle et N n'importe quel point sur AB, et si les demi-cercles sont décrits dans le premier demi-cercle et ayant AN, BN comme diamètres respectivement, la figure comprise entre les circonférences des trois demi-cercles est "ce qu'Archimède a appelé arbelos "; et sa surface est égale au cercle sur PN comme diamètre, où PN est perpendiculaire à AB et rencontre le demi-cercle d'origine en P. ( "Arbelos - le couteau du cordonnier" )
^ Nelsen, RB (2002). "Preuve sans mots: La zone d'un arbelos". Math. Mag . 75 (2): 144. doi : 10.2307 / 3219152 .
^ Boas, Harold P. (2006). "Réflexions sur les Arbelos" . The American Mathematical Monthly . 113 (3): 236–249. doi : 10.2307 / 27641891 . JSTOR 27641891 .
^ Antonio M. Oller-Marcen: "Les f-belos" . Dans: Forum Geometricorum , Volume 13 (2013), pp. 103-111.

Bibliographie

Johnson, RA (1960). Advanced Euclidean Geometry: Un traité élémentaire sur la géométrie du triangle et du cercle (réimpression de l'édition de 1929 par Houghton Miflin ed.). New York: Publications de Douvres. 116-117. ISBN 978-0-486-46237-0 .
Ogilvy, CS (1990). Excursions en géométrie . Douvres. pp. 51-54 . ISBN 0-486-26530-7 . CS1 maint: paramètre découragé ( lien )
Sondow, J. (2012). "Le parbelos, un analogue parabolique des arbelos". arXiv : 1210,2279 [ math.HO ]. American Mathematical Monthly , 120 (2013), 929-935.
Wells, D. (1991). Le dictionnaire Penguin de la géométrie curieuse et intéressante . New York: Livres de pingouin. pp. 5–6 . ISBN 0-14-011813-6 .

Liens externes

Médias liés à Arbelos sur Wikimedia Commons
La définition du dictionnaire de arbelos au Wiktionnaire

[wolfram-1] un ^b Weisstein, Eric W. "Arbelos" . MathWorld .

[archBLprop4-2] Thomas Little Heath (1897), Les œuvres d'Archimède . La presse de l'Universite de Cambridge. Proposition 4 dans le livre des lemmes . Citation: Si AB est le diamètre d'un demi-cercle et N n'importe quel point sur AB, et si les demi-cercles sont décrits dans le premier demi-cercle et ayant AN, BN comme diamètres respectivement, la figure comprise entre les circonférences des trois demi-cercles est "ce qu'Archimède a appelé arbelos "; et sa surface est égale au cercle sur PN comme diamètre, où PN est perpendiculaire à AB et rencontre le demi-cercle d'origine en P. ( "Arbelos - le couteau du cordonnier" )

[RBNelsen_2002-3] Nelsen, RB (2002). "Preuve sans mots: La zone d'un arbelos". Math. Mag . 75 (2): 144. doi : 10.2307 / 3219152 .

[4] Boas, Harold P. (2006). "Réflexions sur les Arbelos" . The American Mathematical Monthly . 113 (3): 236–249. doi : 10.2307 / 27641891 . JSTOR 27641891 .

[5] Antonio M. Oller-Marcen: "Les f-belos" . Dans: Forum Geometricorum , Volume 13 (2013), pp. 103-111.

Languages

In other projects