Théorème de Berry – Esseen - Berry–Esseen theorem

En théorie des probabilités , le théorème de la limite centrale stipule que, dans certaines circonstances, la distribution de probabilité de la moyenne mise à l'échelle d'un échantillon aléatoire converge vers une distribution normale lorsque la taille de l'échantillon augmente à l'infini. Sous des hypothèses plus solides, le théorème de Berry – Esseen , ou inégalité de Berry – Esseen , donne un résultat plus quantitatif, car il spécifie également la vitesse à laquelle cette convergence a lieu en donnant une borne sur l'erreur maximale d' approximation entre la distribution normale et la distribution vraie de la moyenne de l'échantillon mis à l'échelle. L'approximation est mesurée par la distance Kolmogorov – Smirnov . Dans le cas d' échantillons indépendants , le taux de convergence est n ^−1/2 , où n est la taille de l'échantillon, et la constante est estimée en fonction des troisièmes moments normalisés absolus .

Énoncé du théorème

Les déclarations du théorème varient, car il a été découvert indépendamment par deux mathématiciens , Andrew C. Berry (en 1941) et Carl-Gustav Esseen (1942), qui ensuite, avec d'autres auteurs, l'ont raffiné à plusieurs reprises au cours des décennies suivantes.

Sommets distribués à l'identique

Une version, sacrifiant quelque peu la généralité par souci de clarté, est la suivante:

Il existe une constante positive C telle que si X ₁ , X ₂ , ..., sont des variables aléatoires iid avec E ( X ₁ ) = 0, E ( X ₁ ² ) = σ ² > 0, et E (| X ₁ | ³ ) = ρ <∞, et si on définit

${\ displaystyle Y_ {n} = {X_ {1} + X_ {2} + \ cdots + X_ {n} \ over n}}$

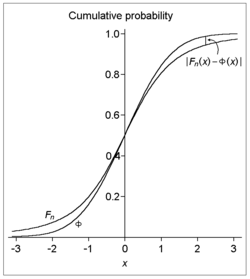
la moyenne de l' échantillon , avec F _n la fonction de distribution cumulative de

${\ displaystyle {Y_ {n} {\ sqrt {n}} \ over {\ sigma}},}$

et Φ la fonction de distribution cumulative de la distribution normale standard , alors pour tout x et n ,

${\ displaystyle \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq {C \ rho \ over \ sigma ^ {3} {\ sqrt {n}}}. \ \ \ \ ( 1)}$

Illustration de la différence des fonctions de distribution cumulative évoquée dans le théorème.

Autrement dit: étant donné une séquence de variables aléatoires indépendantes et distribuées de manière identique , chacune ayant une moyenne nulle et une variance positive , si en plus le troisième moment absolu est fini, alors les fonctions de distribution cumulative de la moyenne standard de l' échantillon et de la distribution normale standard diffèrent (verticalement, sur un graphique) par pas plus que le montant spécifié. Notez que l'erreur d'approximation pour tout n (et donc le taux de convergence limite pour n indéfini suffisamment grand) est bornée par l' ordre de n ^−1/2 .

Les valeurs calculées de la constante C ont nettement diminué au fil des années, passant de la valeur initiale de 7,59 par Esseen (1942) , à 0,7882 par van Beek (1972) , puis 0,7655 par Shiganov (1986) , puis 0,7056 par Shevtsova (2007) , puis 0,7005 par Shevtsova (2008) , puis 0,5894 par Tyurin (2009) , puis 0,5129 par Korolev & Shevtsova (2010a) , puis 0,4785 par Tyurin (2010) . La revue détaillée se trouve dans les articles Korolev & Shevtsova (2010a) et Korolev & Shevtsova (2010b) . La meilleure estimation en 2012, C  <0,4748, découle de l'inégalité

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq {0,33554 (\ rho +0,415 \ sigma ^ {3} ) \ over \ sigma ^ {3} {\ sqrt {n}}},}$

due à Shevtsova (2011) , puisque σ ³  ≤ ρ et 0,33554 · 1,415 <0,4748. Cependant, si ρ ≥ 1,286σ ³ , alors l'estimation

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq {0,3328 (\ rho +0,429 \ sigma ^ {3} ) \ over \ sigma ^ {3} {\ sqrt {n}}},}$

ce qui est également prouvé dans Shevtsova (2011) , donne une estimation supérieure encore plus précise.

Esseen (1956) a prouvé que la constante satisfait également la borne inférieure

${\ displaystyle C \ geq {\ frac {{\ sqrt {10}} + 3} {6 {\ sqrt {2 \ pi}}}} \ approx 0.40973 \ approx {\ frac {1} {\ sqrt {2 \ pi}}} + 0,01079.}$

Sommets distribués de manière non identique

Soit X ₁ , X ₂ , ..., des variables aléatoires indépendantes avec E ( X _i ) = 0, E ( X _i ² ) = σ _i ² > 0, et E (| X _i | ³ ) = ρ _i < ∞. Aussi, laissez

${\ displaystyle S_ {n} = {X_ {1} + X_ {2} + \ cdots + X_ {n} \ over {\ sqrt {\ sigma _ {1} ^ {2} + \ sigma _ {2} ^ {2} + \ cdots + \ sigma _ {n} ^ {2}}}}}$

être la n- ième somme partielle normalisée . Notons F _n le cdf de S _n , et Φ le cdf de la distribution normale standard . Pour des raisons de commodité, notons

${\ displaystyle {\ vec {\ sigma}} = (\ sigma _ {1}, \ ldots, \ sigma _ {n}), \ {\ vec {\ rho}} = (\ rho _ {1}, \ ldots, \ rho _ {n}).}$

En 1941, Andrew C. Berry a prouvé que pour tout n il existe une constante absolue C ₁ telle que

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq C_ {1} \ cdot \ psi _ {1}, \ \ \ \ (2)}$

où

${\ displaystyle \ psi _ {1} = \ psi _ {1} {\ big (} {\ vec {\ sigma}}, {\ vec {\ rho}} {\ big)} = {\ Big (} { \ textstyle \ sum \ limits _ {i = 1} ^ {n} \ sigma _ {i} ^ {2}} {\ Big)} ^ {- 1/2} \ cdot \ max _ {1 \ leq i \ leq n} {\ frac {\ rho _ {i}} {\ sigma _ {i} ^ {2}}}.}$

Indépendamment, en 1942, Carl-Gustav Esseen a prouvé que pour tout n il existe une constante absolue C ₀ telle que

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq C_ {0} \ cdot \ psi _ {0}, \ \ \ \ (3)}$

où

${\ displaystyle \ psi _ {0} = \ psi _ {0} {\ big (} {\ vec {\ sigma}}, {\ vec {\ rho}} {\ big)} = {\ Big (} { \ textstyle \ sum \ limits _ {i = 1} ^ {n} \ sigma _ {i} ^ {2}} {\ Big)} ^ {- 3/2} \ cdot \ sum \ limits _ {i = 1 } ^ {n} \ rho _ {i}.}$

Il est facile de s'assurer que ψ ₀ ≤ψ ₁ . En raison de cette circonstance, l'inégalité (3) est classiquement appelée inégalité de Berry – Esseen, et la quantité ψ ₀ est appelée la fraction de Lyapunov du troisième ordre. De plus, dans le cas où les sommations X ₁ , ..., X _n ont des distributions identiques

${\ displaystyle \ psi _ {0} = \ psi _ {1} = {\ frac {\ rho _ {1}} {\ sigma _ {1} ^ {3} {\ sqrt {n}}}},}$

et ainsi les bornes énoncées par les inégalités (1), (2) et (3) coïncident indépendamment de la constante.

Concernant C ₀ , évidemment, la borne inférieure établie par Esseen (1956) reste valable:

${\ displaystyle C_ {0} \ geq {\ frac {{\ sqrt {10}} + 3} {6 {\ sqrt {2 \ pi}}}} = 0,4097 \ ldots.}$

Les limites supérieures de C ₀ ont ensuite été abaissées de l'estimation originale de 7,59 en raison d' Esseen (1942) à (compte tenu des résultats récents uniquement) 0,9051 en raison de Zolotarev (1967) , 0,7975 en raison de van Beek (1972) , 0,7915 en raison de Shiganov (1986 ) , 0,6379 et 0,5606 dus à Tyurin (2009) et Tyurin (2010) . En 2011, la meilleure estimation est de 0,5600 obtenue par Shevtsova (2010) .

Version multidimensionnelle

Comme pour le théorème de la limite centrale multidimensionnelle , il existe une version multidimensionnelle du théorème de Berry – Esseen.

Soit des vecteurs aléatoires à valeurs indépendantes, chacun ayant une moyenne de zéro. Ecrire et supposer est inversible. Soit une Gaussienne -dimensionnelle avec la même matrice de moyenne et de covariance que . Alors pour tous les ensembles convexes , ${\ displaystyle X_ {1}, \ dots, X_ {n}}$${\ displaystyle \ mathbb {R} ^ {d}}$${\ displaystyle S = \ sum _ {i = 1} ^ {n} X_ {i}}$${\ displaystyle \ Sigma = \ operatorname {Cov} [S]}$${\ displaystyle Z \ sim \ operatorname {N} (0, \ Sigma)}$${\ displaystyle d}$${\ displaystyle S}$${\ displaystyle U \ subseteq \ mathbb {R} ^ {d}}$

${\ displaystyle {\ big |} \ Pr [S \ in U] - \ Pr [Z \ in U] \, {\ big |} \ leq Cd ^ {1/4} \ gamma}$ ,

où est une constante universelle et (la troisième puissance de la norme L ² ). ${\ displaystyle C}$${\ displaystyle \ gamma = \ sum _ {i = 1} ^ {n} \ operatorname {E} {\ big [} \ | \ Sigma ^ {- 1/2} X_ {i} \ | _ {2} ^ {3} {\ big]}}$

La dépendance vis-à-vis de est supposée optimale, mais pourrait ne pas l'être. ${\ displaystyle d ^ {1/4}}$

Voir également

• L'inégalité de Chernoff
• Série Edgeworth
• Liste des inégalités
• Liste des théorèmes mathématiques
• Inégalité de concentration

Remarques

Les références

Liens externes

• Gut, Allan et Holst Lars. Carl-Gustav Esseen , récupéré le 15 mars 2004.
• "Inégalité de Berry-Esseen" , Encyclopédie de mathématiques , EMS Press , 2001 [1994]