Estimation de la densité - Density estimation

Démonstration de l'estimation de la densité à l'aide de l'estimation de la densité du noyau : La vraie densité est le mélange de deux gaussiennes centrées autour de 0 et 3, représentées par une courbe bleue continue. Dans chaque trame, 100 échantillons sont générés à partir de la distribution, indiqués en rouge. Centré sur chaque échantillon, un noyau gaussien est dessiné en gris. La moyenne des gaussiennes donne l'estimation de la densité indiquée dans la courbe noire en pointillés.

En probabilité et en statistique , l' estimation de la densité est la construction d'une estimation , basée sur des données observées , d'une fonction de densité de probabilité sous-jacente non observable . La fonction de densité inobservable est considérée comme la densité selon laquelle une grande population est distribuée ; les données sont généralement considérées comme un échantillon aléatoire de cette population.

Diverses approches d'estimation de la densité sont utilisées, y compris les fenêtres de Parzen et une gamme de techniques de regroupement de données , y compris la quantification vectorielle . La forme la plus basique d'estimation de la densité est un histogramme redimensionné .

Exemple d'estimation de densité

Densité estimée de p (glu | diabète = 1) (rouge), p (glu | diabète = 0) (bleu) et p (glu) (noir)

Probabilité estimée de p (diabète=1 | glu)

Nous examinerons les dossiers de l'incidence du diabète . Ce qui suit est cité textuellement à partir de la description de l' ensemble de données :

Une population de femmes âgées d'au moins 21 ans, d'origine indienne Pima et vivant près de Phoenix, en Arizona, a été testée pour le diabète sucré selon les critères de l' Organisation mondiale de la santé . Les données ont été recueillies par l'Institut national américain du diabète et des maladies digestives et rénales. Nous avons utilisé les 532 enregistrements complets.

Dans cet exemple, nous construisons trois estimations de densité pour "glu" ( concentration de glucose plasmatique), une conditionnelle à la présence de diabète, la seconde conditionnelle à l'absence de diabète et la troisième non conditionnelle au diabète. Les estimations de densité conditionnelles sont ensuite utilisées pour construire la probabilité de diabète conditionnelle à « glu ».

Les données « glu » ont été obtenus à partir de l'ensemble de masse de la langage de programmation R . Dans R, ?Pima.tret ?Pima.tedonner un compte rendu plus complet des données.

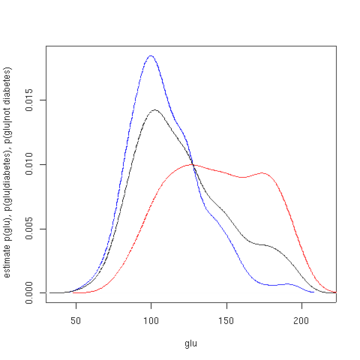
La moyenne de "glu" dans les cas de diabète est de 143,1 et l'écart type est de 31,26. La moyenne de « glu » dans les cas non diabétiques est de 110,0 et l'écart type est de 24,29. De cela, nous voyons que, dans cet ensemble de données, les cas de diabète sont associés à des niveaux plus élevés de « glu ». Ceci sera rendu plus clair par les tracés des fonctions de densité estimées.

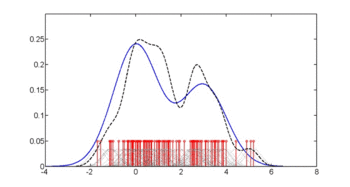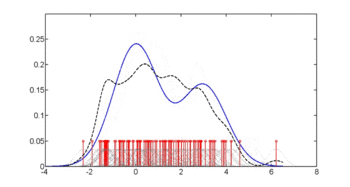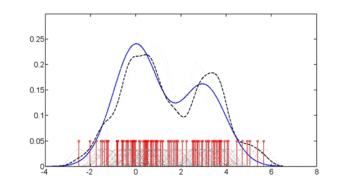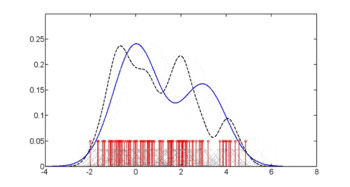
La première figure montre les estimations de densité de p (glu | diabète=1), p (glu | diabète=0) et p (glu). Les estimations de densité sont des estimations de densité de noyau utilisant un noyau gaussien. C'est-à-dire qu'une fonction de densité gaussienne est placée à chaque point de données, et la somme des fonctions de densité est calculée sur la plage des données.

A partir de la densité de « glu » conditionnelle au diabète, on peut obtenir la probabilité de diabète conditionnelle à « glu » via la règle de Bayes . Par souci de concision, « diabète » est abrégé « db ». dans cette formule.

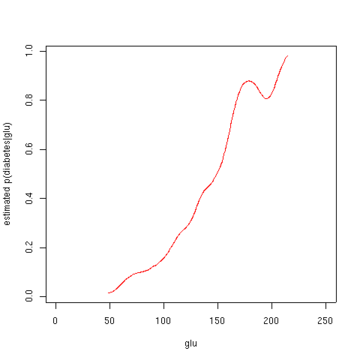
p({\mbox{diabète}}=1|{\mbox{glu}})={\frac {p({\mbox{glu}}|{\mbox{db.}}=1)\ ,p({\mbox{db.}}=1)}{p({\mbox{glu}}|{\mbox{db.}}=1)\,p({\mbox{db.}}= 1)+p({\mbox{glu}}|{\mbox{db.}}=0)\,p({\mbox{db.}}=0)}}

La deuxième figure montre la probabilité a posteriori estimée p (diabète=1 | glu). A partir de ces données, il apparaît qu'un niveau accru de "glu" est associé au diabète.

Scénario par exemple

Les commandes R suivantes créeront les figures ci-dessus. Ces commandes peuvent être entrées à l'invite de commande en utilisant le copier-coller.

library(MASS)
data(Pima.tr)
data(Pima.te)

Pima <- rbind (Pima.tr, Pima.te)
glu  <- Pima[, 'glu']

d0 <- Pima[, 'type'] == 'No'
d1 <- Pima[, 'type'] == 'Yes'
base.rate.d1 <- sum(d1) / (sum(d1) + sum(d0))

glu.density    <- density (glu)
glu.d0.density <- density (glu[d0])
glu.d1.density <- density (glu[d1])

glu.d0.f <- approxfun(glu.d0.density$x, glu.d0.density$y)
glu.d1.f <- approxfun(glu.d1.density$x, glu.d1.density$y)

p.d.given.glu <- function(glu, base.rate.d1)
{
    p1 <- glu.d1.f(glu) * base.rate.d1
    p0 <- glu.d0.f(glu) * (1 - base.rate.d1)
    p1 / (p0 + p1)
}

x <- 1:250
y <- p.d.given.glu (x, base.rate.d1)
plot(x, y, type='l', col='red', xlab='glu', ylab='estimated p(diabetes|glu)')

plot(density(glu[d0]), col='blue', xlab='glu', ylab='estimate p(glu), 
     p(glu|diabetes), p(glu|not diabetes)', main=NA)
lines(density(glu[d1]), col='red')

Notez que l'estimateur de densité conditionnelle ci-dessus utilise des bandes passantes qui sont optimales pour les densités inconditionnelles. Alternativement, on pourrait utiliser la méthode de Hall, Racine et Li (2004) et le progiciel R np pour la sélection automatique de la bande passante (induite par les données) qui est optimale pour les estimations de densité conditionnelles ; voir la vignette np pour une introduction au package np. Les commandes R suivantes utilisent la npcdens()fonction pour fournir un lissage optimal. Notez que la réponse "Oui"/"Non" est un facteur.

library(np)

fy.x <- npcdens(type~glu, nmulti=1, data=Pima)

Pima.eval <- data.frame(type=factor("Yes"),
                        glu=seq(min(Pima$glu), max(Pima$glu), length=250))
 
plot(x, y, type='l', lty=2, col='red', xlab='glu',
     ylab='estimated p(diabetes|glu)')
lines(Pima.eval$glu, predict(fy.x, newdata=Pima.eval), col="blue")
legend(0, 1, c("Unconditional bandwidth", "Conditional bandwidth"),
       col=c("red", "blue"), lty=c(2, 1))

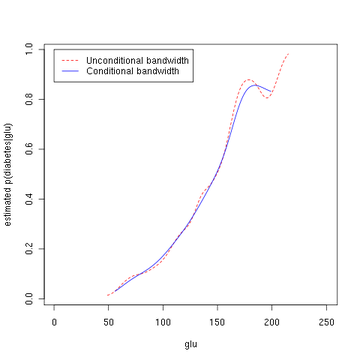
La troisième figure utilise un lissage optimal via la méthode de Hall, Racine et Li indiquant que la bande passante de densité inconditionnelle utilisée dans la deuxième figure ci-dessus donne une estimation de densité conditionnelle qui peut être quelque peu sous-lissée.

Application et objectif

Une utilisation très naturelle des estimations de densité est l'étude informelle des propriétés d'un ensemble donné de données. Les estimations de densité peuvent donner des indications précieuses sur des caractéristiques telles que l'asymétrie et la multimodalité des données. Dans certains cas, ils aboutiront à des conclusions qui pourront alors être considérées comme évidentes en soi, tandis que dans d'autres, ils ne feront qu'indiquer la voie à suivre pour une analyse plus approfondie et/ou une collecte de données.

Histogramme et fonction de densité pour une distribution de Gumbel

Un aspect important des statistiques est souvent la présentation des données au client afin de fournir une explication et une illustration des conclusions qui peuvent éventuellement avoir été obtenues par d'autres moyens. Les estimations de densité sont idéales à cette fin, pour la simple raison qu'elles sont assez facilement compréhensibles pour les non mathématiciens.

D'autres exemples illustrant l'utilisation des estimations de densité à des fins exploratoires et de présentation, y compris le cas important des données bivariées.

L'estimation de la densité est également fréquemment utilisée dans la détection d'anomalies ou de nouveautés : si une observation se situe dans une région de très faible densité, il s'agit probablement d'une anomalie ou d'une nouveauté.

En hydrologie, l' histogramme et la fonction de densité estimée des données de précipitations et de débits fluviaux, analysés avec une distribution de probabilité , sont utilisés pour mieux comprendre leur comportement et leur fréquence d'occurrence. Un exemple est montré dans la figure bleue.

Voir également

Les références

Sources

Brian D. Ripley (1996). Reconnaissance de formes et réseaux de neurones . Cambridge : Cambridge University Press. ISBN 978-0521460866.
Trevor Hastie , Robert Tibshirani et Jérôme Friedman. Les éléments de l'apprentissage statistique . New York : Springer, 2001. ISBN 0-387-95284-5 . (Voir chapitre 6.)
Qi Li et Jeffrey S. Racine. Econométrie non paramétrique : théorie et pratique . Princeton University Press, 2007, ISBN 0-691-12161-3 . (Voir chapitre 1.)
DW Scott. Estimation de la densité multivariée. Théorie, pratique et visualisation . New York : Wiley, 1992.
BW Silverman . Estimation de la densité . Londres : Chapman et Hall, 1986. ISBN 978-0-412-24620-3

Liens externes

CREEM : Centre de recherche sur la modélisation écologique et environnementale Téléchargements gratuits de progiciels d'estimation de la densité Distance 4 (de l'Unité de recherche pour l'évaluation des populations fauniques « RUWPA ») et WiSP .
Résumé du contenu du référentiel d'apprentissage automatique de l'UCI (voir "Base de données sur le diabète des Indiens Pima" pour l'ensemble de données d'origine de 732 enregistrements et des notes supplémentaires.)
Code MATLAB pour l' estimation de la densité unidimensionnelle et bidimensionnelle
Logiciel libAGF C++ pour l' estimation de la densité de noyau variable .

Languages

In other projects