Horizon - Horizon

Un horizon désertique élevé au coucher du soleil , Californie , USA

L' horizon ou la ligne d' horizon est la ligne apparente qui sépare la terre du ciel , la ligne qui divise toutes les directions visibles en deux catégories: celles qui coupent la surface de la Terre et celles qui ne le font pas. Le véritable horizon est en fait une ligne théorique, qui ne peut être observée que lorsqu'elle se trouve à la surface de la mer. À de nombreux endroits, cette ligne est obscurcie par la terre, les arbres, les bâtiments, les montagnes, etc., et l'intersection résultante de la terre et du ciel est appelée l' horizon visible . Quand on regarde une mer depuis un rivage, la partie de la mer la plus proche de l'horizon est appelée le large .

Le véritable horizon est horizontal. Il entoure l'observateur et il est généralement supposé être un cercle, dessiné sur la surface d'un modèle parfaitement sphérique de la Terre . Son centre est en dessous de l'observateur et au - dessous du niveau de la mer . Sa distance de l'observateur varie d'un jour à l'autre en raison de la réfraction atmosphérique , qui est grandement affectée par les conditions météorologiques . De plus, plus les yeux de l'observateur sont élevés par rapport au niveau de la mer, plus l'horizon est éloigné de l'observateur. Par exemple, dans des conditions atmosphériques standard , pour un observateur dont le niveau des yeux est au-dessus du niveau de la mer de 1,70 mètre (5 pieds 7 pouces), l'horizon est à une distance d'environ 5 kilomètres (3,1 miles).

Lorsqu'il est observé à partir de points de vue très élevés, comme une station spatiale , l'horizon est beaucoup plus éloigné et englobe une zone beaucoup plus grande de la surface de la Terre. Dans ce cas, il devient évident que l'horizon ressemble plus à une ellipse qu'à un cercle parfait, surtout lorsque l'observateur est au-dessus de l'équateur, et que la surface de la Terre peut être mieux modélisée comme un ellipsoïde que comme une sphère.

Le mot horizon dérive du grec «ὁρίζων κύκλος» horizōn kyklos , «cercle de séparation», où «ὁρίζων» est du verbe ὁρίζω horizō , «diviser», «séparer», qui à son tour dérive de «ὅρος» ( oros ), "frontière, repère".

Apparence et utilisation

Vue sur l'océan avec un navire près de l'horizon

Historiquement, la distance à l'horizon visible a longtemps été vitale pour la survie et la réussite de la navigation, notamment en mer, car elle déterminait la portée maximale de la vision et donc de la communication d' un observateur , avec toutes les conséquences évidentes pour la sécurité et la transmission d'informations gamme implicite. Cette importance a diminué avec le développement de la radio et du télégraphe , mais même aujourd'hui, lors du pilotage d'un aéronef selon les règles de vol à vue , une technique appelée vol en assiette est utilisée pour contrôler l'aéronef, où le pilote utilise la relation visuelle entre le nez de l'aéronef et l'horizon pour contrôler l'avion. Un pilote peut également conserver son orientation spatiale en se référant à l'horizon.

Dans de nombreux contextes, en particulier le dessin en perspective , la courbure de la Terre est ignorée et l'horizon est considéré comme la ligne théorique vers laquelle convergent des points sur n'importe quel plan horizontal (lorsqu'ils sont projetés sur le plan de l'image) à mesure que leur distance par rapport à l'observateur augmente. Pour les observateurs près du niveau de la mer, la différence entre cet horizon géométrique (qui suppose un plan de sol parfaitement plat et infini) et le véritable horizon (qui suppose une surface terrestre sphérique ) est imperceptible à l'œil nu (mais pour quelqu'un sur une colline de 1000 mètres face à la mer, le véritable horizon sera d'environ un degré au-dessous d'une ligne horizontale).

En astronomie, l'horizon est le plan horizontal à travers les yeux de l'observateur. C'est le plan fondamental du système de coordonnées horizontales , le lieu des points qui ont une altitude de zéro degré. Bien que similaire à l'horizon géométrique, dans ce contexte, un horizon peut être considéré comme un plan dans l'espace, plutôt qu'une ligne sur un plan d'image.

Distance à l'horizon

En ignorant l' effet de la réfraction atmosphérique , la distance à l'horizon réel d'un observateur proche de la surface de la Terre est d'environ

${\ Displaystyle d \ approx {\ sqrt {2 \, h \, R}} \ ,,}$

où h est la hauteur au - dessus du niveau de la mer et R est le rayon de la Terre .

Lorsque d est mesuré en kilomètres et h en mètres, la distance est

${\ displaystyle d \ environ 3,57 {\ sqrt {h}} \ ,,}$

où la constante 3,57 a des unités de km / m ^½ .

Lorsque d est mesuré en miles (miles terrestres, c'est-à-dire "miles terrestres" de 5 280 pieds (1609,344 m)) et h en pieds, la distance est

${\ displaystyle d \ approx {\ sqrt {1.5h}} \ approx 1.22 {\ sqrt {h}} \ ,.}$

où la constante 1,22 a des unités de mi / pi ^½ .

Dans cette équation, la surface de la Terre est supposée être parfaitement sphérique, avec r égal à environ 6 371 kilomètres (3 959 mi).

Exemples

En supposant aucune réfraction atmosphérique et une Terre sphérique avec un rayon R = 6371 kilomètres (3,959 mi):

• Pour un observateur debout au sol avec h = 1,70 mètre (5 pi 7 po), l'horizon est à une distance de 4,7 kilomètres (2,9 mi).
• Pour un observateur debout au sol avec h = 2 mètres (6 pieds 7 pouces), l'horizon est à une distance de 5 kilomètres (3,1 mi).
• Pour un observateur debout sur une colline ou une tour à 30 mètres (98 pieds) au-dessus du niveau de la mer, l'horizon est à une distance de 19,6 kilomètres (12,2 mi).
• Pour un observateur debout sur une colline ou une tour à 100 mètres (330 pieds) au-dessus du niveau de la mer, l'horizon est à une distance de 36 kilomètres (22 mi).
• Pour un observateur debout sur le toit du Burj Khalifa , à 828 mètres (2717 pieds) du sol et à environ 834 mètres (2736 pieds) au-dessus du niveau de la mer, l'horizon est à une distance de 103 kilomètres (64 mi).
• Pour un observateur au sommet du mont Everest (8848 mètres (29029 pieds) d'altitude), l'horizon est à une distance de 336 kilomètres (209 mi).
• Pour un pilote de U-2 , alors qu'il vole à son plafond de service de 21 000 mètres (69 000 pieds), l'horizon est à une distance de 521 kilomètres (324 mi).

D'autres planètes

Sur les planètes terrestres et autres corps célestes solides avec des effets atmosphériques négligeables, la distance à l'horizon pour un «observateur standard» varie comme la racine carrée du rayon de la planète. Ainsi, l'horizon sur Mercure est 62% aussi éloigné de l'observateur que sur Terre, sur Mars le chiffre est de 73%, sur la Lune le chiffre est de 52%, sur Mimas le chiffre est de 18%, et ainsi de suite.

Dérivation

Base géométrique pour le calcul de la distance à l'horizon, théorème de la tangente sécante

Distance géométrique à l'horizon, théorème de Pythagore

Trois types d'horizon

Si la Terre est supposée être une sphère sans relief (plutôt qu'un sphéroïde aplati ) sans réfraction atmosphérique, alors la distance à l'horizon peut être facilement calculée.

Le théorème sécant-tangent déclare que

${\ displaystyle \ mathrm {OC} ^ {2} = \ mathrm {OA} \ times \ mathrm {OB} \ ,.}$

Effectuez les substitutions suivantes:

• d = OC = distance à l'horizon
• D = AB = diamètre de la Terre
• h = OB = hauteur de l'observateur au-dessus du niveau de la mer
• D + h = OA = diamètre de la Terre plus hauteur de l'observateur au-dessus du niveau de la mer,

avec d, D et h tous mesurés dans les mêmes unités. La formule devient maintenant

${\ Displaystyle d ^ {2} = h (D + h) \, \!}$

ou

${\ displaystyle d = {\ sqrt {h (D + h)}} = {\ sqrt {h (2R + h)}} \ ,,}$

où R est le rayon de la Terre .

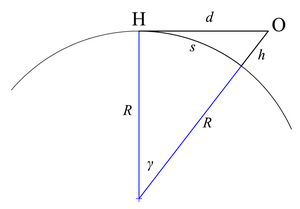
La même équation peut également être dérivée en utilisant le théorème de Pythagore . À l'horizon, la ligne de visée est une tangente à la Terre et est également perpendiculaire au rayon de la Terre. Cela met en place un triangle rectangle, avec la somme du rayon et de la hauteur comme hypoténuse. Avec

• d = distance à l'horizon
• h = hauteur de l'observateur au-dessus du niveau de la mer
• R = rayon de la Terre

se référer à la deuxième figure à droite conduit à ce qui suit:

${\ Displaystyle (R + h) ^ {2} = R ^ {2} + d ^ {2} \, \!}$

${\ displaystyle R ^ {2} + 2Rh + h ^ {2} = R ^ {2} + d ^ {2} \, \!}$

${\ displaystyle d = {\ sqrt {h (2R + h)}} \ ,.}$

La formule exacte ci-dessus peut être développée comme suit:

${\ displaystyle d = {\ sqrt {2Rh + h ^ {2}}} \ ,,}$

où R est le rayon de la Terre ( R et h doivent être dans les mêmes unités). Par exemple, si un satellite est à une hauteur de 2000 km, la distance à l'horizon est de 5 430 kilomètres (3 370 mi); négliger le deuxième terme entre parenthèses donnerait une distance de 5 048 kilomètres (3 137 mi), une erreur de 7%.

Approximation

Graphiques des distances à l'horizon réel sur Terre pour une hauteur donnée h . s est le long de la surface de la Terre, d est la distance en ligne droite, et ~ d est la distance approximative en ligne droite en supposant h << le rayon de la Terre, 6371 km. Dans l'image SVG , passez la souris sur un graphique pour le mettre en surbrillance.

Si l'observateur est proche de la surface de la terre, alors il est valide de ne pas tenir compte de h dans le terme (2 R + h ) , et la formule devient-

${\ displaystyle d = {\ sqrt {2Rh}} \ ,.}$

En utilisant des kilomètres pour d et R , et des mètres pour h , et en prenant le rayon de la Terre à 6371 km, la distance à l'horizon est

${\ displaystyle d \ approx {\ sqrt {2 \ cdot 6371 \ cdot {h / 1000}}} \ approx 3.570 {\ sqrt {h}} \,}$.

En utilisant les unités impériales , avec d et R en milles terrestres (couramment utilisés sur terre), et h en pieds, la distance à l'horizon est

${\ displaystyle d \ approx {\ sqrt {2 \ cdot 3963 \ cdot {h / 5280}}} \ approx {\ sqrt {1.5h}} \ approx 1.22 {\ sqrt {h}}}$.

Si d est en miles nautiques et h en pieds, le facteur constant est d'environ 1,06, ce qui est suffisamment proche de 1 pour qu'il soit souvent ignoré, ce qui donne:

${\ displaystyle d \ approx {\ sqrt {h}}}$

Ces formules peuvent être utilisées lorsque h est beaucoup plus petit que le rayon de la Terre (6371 km ou 3959 mi), y compris toutes les vues de tout sommet de montagne, avion ou ballon à haute altitude. Avec les constantes telles que données, les formules métriques et impériales sont toutes deux précises à 1% près (voir la section suivante pour savoir comment obtenir une plus grande précision). Si h est significatif par rapport à R , comme avec la plupart des satellites , l'approximation n'est plus valide et la formule exacte est requise.

Autres mesures

Distance d'arc

Une autre relation implique la distance du grand cercle s le long de l' arc sur la surface courbe de la Terre jusqu'à l'horizon; avec γ en radians ,

${\ displaystyle s = R \ gamma \ ,;}$

puis

${\ displaystyle \ cos \ gamma = \ cos {\ frac {s} {R}} = {\ frac {R} {R + h}} \ ,.}$

Résoudre pour s donne

${\ displaystyle s = R \ cos ^ {- 1} {\ frac {R} {R + h}} \ ,.}$

La distance s peut également être exprimée en termes de distance de ligne de visée d ; à partir du deuxième chiffre à droite,

${\ displaystyle \ tan \ gamma = {\ frac {d} {R}} \ ,;}$

remplacer γ et réorganiser donne

${\ displaystyle s = R \ tan ^ {- 1} {\ frac {d} {R}} \ ,.}$

Les distances d et s sont à peu près les mêmes lorsque la hauteur de l'objet est négligeable par rapport au rayon (c'est-à-dire h  ≪  R ).

Angle zénith

Angle zénithal maximal pour un observateur élevé dans une atmosphère sphérique homogène

Lorsque l'observateur est élevé, l' angle zénithal de l'horizon peut être supérieur à 90 °. L'angle zénithal visible maximal se produit lorsque le rayon est tangent à la surface de la Terre; du triangle OCG dans la figure de droite,

${\ displaystyle \ cos \ gamma = {\ frac {R} {R + h}}}$

où est la hauteur de l'observateur au-dessus de la surface et est l'inclinaison angulaire de l'horizon. Il est lié à l'angle zénithal de l'horizon par: ${\ displaystyle h}$${\ displaystyle \ gamma}$${\ displaystyle z}$

${\ displaystyle z = \ gamma +90 {} ^ {\ circ}}$

Pour une hauteur non négative , l'angle est toujours ≥ 90 °. ${\ displaystyle h}$${\ displaystyle z}$

Objets au-dessus de l'horizon

Distance d'horizon géométrique

Pour calculer la plus grande distance à laquelle un observateur peut voir le sommet d'un objet au-dessus de l'horizon, calculez la distance à l'horizon pour un observateur hypothétique au-dessus de cet objet et ajoutez-la à la distance de l'observateur réel à l'horizon. Par exemple, pour un observateur d'une hauteur de 1,70 m debout au sol, l'horizon est à 4,65 km. Pour une tour d'une hauteur de 100 m, la distance à l'horizon est de 35,7 km. Ainsi, un observateur sur une plage peut voir le sommet de la tour tant qu'elle n'est pas à plus de 40,35 km. À l'inverse, si un observateur sur un bateau ( h = 1,7 m ) peut juste voir la cime des arbres sur une rive voisine ( h = 10 m ), les arbres sont probablement à environ 16 km.

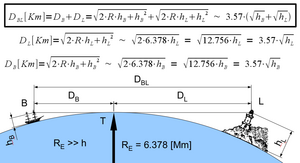
En se référant à la figure de droite, le haut du phare sera visible à un belvédère dans un nid de pie au sommet d'un mât du bateau si

${\ displaystyle D _ {\ mathrm {BL}} <3,57 \, ({\ sqrt {h _ {\ mathrm {B}}}} + {\ sqrt {h _ {\ mathrm {L}}}}) \ ,,}$

où D _BL est en kilomètres et h _B et h _L sont en mètres.

Une vue sur une baie de 20 km de large sur la côte espagnole . Notez la courbure de la Terre cachant la base des bâtiments de l'autre côté.

Comme autre exemple, supposons qu'un observateur, dont les yeux sont à deux mètres au-dessus du sol, utilise des jumelles pour regarder un bâtiment éloigné qu'il sait se composer de trente étages , chacun de 3,5 mètres de haut. Il compte les étages qu'il peut voir et constate qu'il n'y en a que dix. Ainsi, vingt étages ou 70 mètres du bâtiment lui sont cachés par la courbure de la Terre. À partir de là, il peut calculer sa distance du bâtiment:

${\ displaystyle D \ environ 3,57 ({\ sqrt {2}} + {\ sqrt {70}})}$

ce qui fait environ 35 kilomètres.

Il est également possible de calculer la quantité d'un objet distant visible au-dessus de l'horizon. Supposons que l'œil d'un observateur se trouve à 10 mètres au-dessus du niveau de la mer et qu'il regarde un navire à 20 km. Son horizon est:

${\ displaystyle 3.57 {\ sqrt {10}}}$

kilomètres de lui, ce qui revient à environ 11,3 kilomètres. Le navire est à 8,7 km. La hauteur d'un point sur le navire qui est juste visible par l'observateur est donnée par:

${\ Displaystyle h \ approx \ left ({\ frac {8.7} {3.57}} \ right) ^ {2}}$

qui atteint presque exactement six mètres. L'observateur peut donc voir la partie du navire qui se trouve à plus de six mètres au-dessus du niveau de l'eau. La partie du navire qui se trouve en dessous de cette hauteur lui est cachée par la courbure de la Terre. Dans cette situation, on dit que le navire est coque en bas .

Effet de la réfraction atmosphérique

En raison de la réfraction atmosphérique, la distance à l'horizon visible est supérieure à la distance basée sur un simple calcul géométrique. Si la surface du sol (ou de l'eau) est plus froide que l'air au-dessus, une couche d'air froide et dense se forme près de la surface, provoquant la réfraction de la lumière vers le bas lorsqu'elle se déplace, et donc, dans une certaine mesure, de contourner le courbure de la Terre. L'inverse se produit si le sol est plus chaud que l'air au-dessus, comme cela se produit souvent dans les déserts, produisant des mirages . En guise de compensation approximative de la réfraction, les géomètres mesurant des distances supérieures à 100 mètres soustraient 14% de l'erreur de courbure calculée et s'assurent que les lignes de visée sont à au moins 1,5 mètre du sol, afin de réduire les erreurs aléatoires créées par la réfraction.

Horizon typique du désert

Si la Terre était un monde sans air comme la Lune, les calculs ci-dessus seraient exacts. Cependant, la Terre possède une atmosphère d'air , dont la densité et l' indice de réfraction varient considérablement en fonction de la température et de la pression. Cela permet à l'air de réfracter la lumière à des degrés divers, affectant l'apparence de l'horizon. Habituellement, la densité de l'air juste au-dessus de la surface de la Terre est supérieure à sa densité à des altitudes plus élevées. Cela rend son indice de réfraction plus grand près de la surface qu'à des altitudes plus élevées, ce qui fait que la lumière qui se déplace approximativement horizontalement est réfractée vers le bas. Cela rend la distance réelle à l'horizon supérieure à la distance calculée avec des formules géométriques. Avec des conditions atmosphériques standard, la différence est d'environ 8%. Cela change le facteur de 3,57, dans les formules métriques utilisées ci-dessus, à environ 3,86. Par exemple, si un observateur se tient au bord de la mer, avec les yeux à 1,70 m au-dessus du niveau de la mer, selon les formules géométriques simples données au-dessus de l'horizon, il devrait être à 4,7 km. En fait, la réfraction atmosphérique permet à l'observateur de voir 300 mètres plus loin, déplaçant le véritable horizon à 5 km de l'observateur.

Cette correction peut être, et est souvent, appliquée comme une assez bonne approximation lorsque les conditions atmosphériques sont proches de la norme . Lorsque les conditions sont inhabituelles, cette approximation échoue. La réfraction est fortement affectée par les gradients de température, qui peuvent varier considérablement d'un jour à l'autre, surtout au-dessus de l'eau. Dans les cas extrêmes, généralement au printemps, lorsque l'air chaud recouvre l'eau froide, la réfraction peut permettre à la lumière de suivre la surface de la Terre sur des centaines de kilomètres. Des conditions opposées se produisent, par exemple, dans les déserts, où la surface est très chaude, de sorte que l'air chaud à faible densité se trouve sous l'air plus froid. Cela provoque la réfraction de la lumière vers le haut, provoquant des effets de mirage qui rendent le concept d'horizon quelque peu dénué de sens. Les valeurs calculées des effets de la réfraction dans des conditions inhabituelles ne sont donc qu'approximatives. Néanmoins, des tentatives ont été faites pour les calculer plus précisément que la simple approximation décrite ci-dessus.

En dehors de la plage de longueur d'onde visuelle, la réfraction sera différente. Pour le radar (par exemple pour des longueurs d'onde de 300 à 3 mm, c'est-à-dire des fréquences comprises entre 1 et 100 GHz), le rayon de la Terre peut être multiplié par 4/3 pour obtenir un rayon effectif donnant un facteur de 4,12 dans la formule métrique, c'est-à-dire que l'horizon radar sera 15% au-delà de l'horizon géométrique ou 7% au-delà du visuel. Le facteur 4/3 n'est pas exact, car dans le cas visuel, la réfraction dépend des conditions atmosphériques.

Méthode d'intégration - Sweer

Si le profil de densité de l'atmosphère est connu, la distance d à l'horizon est donnée par

${\ displaystyle d = {{R} _ {\ text {E}}} \ left (\ psi + \ delta \ right) \ ,,}$

où R _E est le rayon de la Terre, ψ est le pendage de l'horizon et δ est la réfraction de l'horizon. Le creux est déterminé assez simplement à partir de

${\ displaystyle \ cos \ psi = {\ frac {{R} _ {\ text {E}} {\ mu} _ {0}} {\ left ({{R} _ {\ text {E}}} + h \ droite) \ mu}} \ ,,}$

où h est la hauteur de l'observateur au-dessus de la Terre, μ est l'indice de réfraction de l'air à la hauteur de l'observateur et μ ₀ est l'indice de réfraction de l'air à la surface de la Terre.

La réfraction doit être trouvée par intégration de

${\ displaystyle \ delta = - \ int _ {0} ^ {h} {\ tan \ phi {\ frac {{\ text {d}} \ mu} {\ mu}}} \ ,,}$

où est l'angle entre le rayon et une ligne passant par le centre de la Terre. Les angles ψ et sont liés par ${\ displaystyle \ phi \, \!}$${\ displaystyle \ phi \, \!}$

${\ displaystyle \ phi = 90 {} ^ {\ circ} - \ psi \ ,.}$

Méthode simple - Young

Une approche beaucoup plus simple, ce qui produit essentiellement les mêmes résultats que l'approximation de premier ordre décrit ci - dessus, utilise le modèle géométrique mais utilise un rayon R ' = 7/6 R _E . La distance à l'horizon est alors

${\ displaystyle d = {\ sqrt {2R ^ {\ prime} h}} \ ,.}$

En prenant le rayon de la Terre à 6371 km, avec d en km et h en m,

${\ Displaystyle d \ environ 3,86 {\ sqrt {h}} \ ,;}$

avec d en mi et h en ft,

${\ displaystyle d \ environ 1,32 {\ sqrt {h}} \ ,.}$

Les résultats de la méthode de Young sont assez proches de ceux de la méthode de Sweer et sont suffisamment précis à de nombreuses fins.

Courbure de l'horizon

La courbure de l'horizon est facilement visible sur cette photographie de 2008, prise depuis une navette spatiale à une altitude de 226 km (140 mi).

D'un point au-dessus de la surface de la Terre, l'horizon apparaît légèrement convexe ; c'est un arc de cercle . La formule suivante exprime la relation géométrique de base entre cette courbure visuelle , l'altitude et le rayon de la Terre : ${\ displaystyle \ kappa}$${\ displaystyle h}$${\ displaystyle R}$

${\ displaystyle \ kappa = {\ sqrt {\ left (1 + {\ frac {h} {R}} \ right) ^ {2} -1}} \}$

La courbure est l'inverse du rayon angulaire de courbure en radians . Une courbure de 1,0 apparaît comme un cercle d'un rayon angulaire de 57,3 ° correspondant à une altitude d'environ 2 640 km (1 640 mi) au-dessus de la surface de la Terre. À une altitude de 10 km (6,2 mi; 33000 ft), l' altitude de croisière d'un avion de ligne typique, la courbure mathématique de l'horizon est d'environ 0,056, la même courbure du bord du cercle avec un rayon de 10 m qui est vue de 56 cm directement au-dessus du centre du cercle. Cependant, la courbure apparente est inférieure à celle due à la réfraction de la lumière par l'atmosphère et à l' obscurcissement de l'horizon par de hautes couches nuageuses qui réduisent l'altitude au-dessus de la surface visuelle.

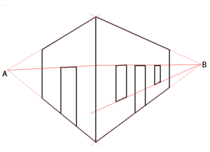
Points de fuite

Deux points à l'horizon se trouvent aux intersections des lignes prolongeant les segments représentant les bords du bâtiment au premier plan. La ligne d'horizon coïncide ici avec la ligne en haut des portes et fenêtres.

L'horizon est une caractéristique clé du plan de l' image dans la science de la perspective graphique . En supposant que le plan d'image se vertical à la masse, et P est la projection perpendiculaire du point oculaire O sur le plan d'image, l'horizon est définie comme étant la ligne horizontale passant par P . Le point P est le point de fuite des lignes perpendiculaires à l'image. Si S est un autre point sur l'horizon, alors c'est le point de fuite pour toutes les droites parallèles à OS . Mais Brook Taylor (1719) a indiqué que le plan d'horizon déterminé par O et l'horizon était comme n'importe quel autre plan :

Le terme de ligne horizontale, par exemple, est susceptible de confiner les notions d'un apprenant au plan de l'horizon, et de lui faire imaginer que ce plan jouit de privilèges particuliers, qui rendent les figures plus faciles et plus pratiques. être décrit, au moyen de cette ligne horizontale, que les figures dans n'importe quel autre plan;… Mais dans ce livre, je ne fais aucune différence entre le plan de l'horizon, et tout autre plan que ce soit ...

La géométrie particulière de la perspective où les lignes parallèles convergent au loin, a stimulé le développement de la géométrie projective qui pose un point à l'infini où les lignes parallèles se rencontrent. Dans son livre Geometry of an Art (2007), Kirsti Andersen a décrit l'évolution du dessin en perspective et de la science jusqu'en 1800, notant que les points de fuite n'ont pas besoin d'être à l'horizon. Dans un chapitre intitulé «Horizon», John Stillwell a raconté comment la géométrie projective a conduit à la géométrie d'incidence , l'étude abstraite moderne de l'intersection des lignes. Stillwell s'est également aventuré dans les fondements des mathématiques dans une section intitulée "Quelles sont les lois de l'algèbre?" L '«algèbre des points», à l'origine donnée par Karl von Staudt en dérivant les axiomes d'un champ, a été déconstruite au XXe siècle, offrant une grande variété de possibilités mathématiques. États Stillwell

Cette découverte d'il y a 100 ans semble capable de bouleverser les mathématiques, bien qu'elle n'ait pas encore été totalement absorbée par la communauté mathématique. Non seulement cela défie la tendance à transformer la géométrie en algèbre, mais cela suggère que la géométrie et l'algèbre ont une base plus simple qu'on ne le pensait auparavant.

Voir également

• Art du paysage aérien
• Réfraction atmosphérique
• Aube
• Crépuscule
• Horizontal et vertical
• Paysage
  • Art du paysage
• Membre
  • Assombrissement des membres
  • Membre lunaire
• Horizon radar
• Horizon radio
• Sextant

Les références

Lectures complémentaires

• Jeune, Andrew T. "Dip of the Horizon" . Site Web de Green Flash (sections: Réfraction astronomique, regroupement d'horizon) . Département d'astronomie de l'Université d'État de San Diego . Récupéré le 16 avril 2011 .

Liens externes