Le paradoxe de Hilbert du Grand Hôtel - Hilbert's paradox of the Grand Hotel

Le paradoxe de Hilbert du Grand Hôtel ( familier : Infinite Hotel Paradox ou Hilbert's Hotel ) est une expérience de pensée qui illustre une propriété contre - intuitive des ensembles infinis. Il est démontré qu'un hôtel entièrement occupé avec une infinité de chambres peut encore accueillir des invités supplémentaires, voire une infinité d'entre eux, et ce processus peut être répété à l'infini. L'idée a été introduite par David Hilbert dans une conférence de 1924 "Über das Unendliche", réimprimée dans ( Hilbert 2013 , p.730), et a été popularisée par le livre de George Gamow en 1947, One Two Three... Infinity .

Le paradoxe

Considérons un hôtel hypothétique avec un nombre infini de chambres, toutes occupées. On pourrait être tenté de penser que l'hôtel ne serait pas en mesure d'accueillir les nouveaux arrivants, comme ce serait le cas avec un nombre fini de chambres, où le principe du casier s'appliquerait.

Finis beaucoup de nouveaux invités

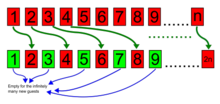
Supposons qu'un nouveau client arrive et souhaite être hébergé à l'hôtel. Nous pouvons (simultanément) déplacer le client actuellement de la chambre 1 vers la chambre 2, le client actuellement de la chambre 2 vers la chambre 3, et ainsi de suite, en déplaçant chaque client de sa chambre actuelle n vers la chambre n +1. Après cela, la chambre 1 est vide et le nouveau client peut être déplacé dans cette chambre. En répétant cette procédure, il est possible de faire de la place pour un nombre fini de nouveaux invités. En général, supposons que k invités recherchent une chambre. Nous pouvons appliquer la même procédure et déplacer chaque invité de la chambre n à la chambre n + k . De la même manière, si k clients souhaitent quitter l'hôtel, chaque client passe de la chambre n à la chambre n − k .

Infiniment beaucoup de nouveaux invités

Il est également possible d'accueillir un nombre infiniment dénombrable de nouveaux clients : il suffit de déplacer la personne occupant la chambre 1 vers la chambre 2, le client occupant la chambre 2 vers la chambre 4, et, en général, le client occupant la chambre n vers la chambre 2 n (2 fois n ), et toutes les chambres impaires (qui sont dénombrables à l'infini) seront gratuites pour les nouveaux invités.

Une infinité d'autocars avec une infinité d'invités chacun

Il est possible d'accueillir une infinité de wagons de passagers dénombrables chacun, par plusieurs méthodes différentes. La plupart des méthodes dépendent du fait que les sièges dans les voitures sont déjà numérotés (ou utilisent l' axiome du choix comptable ). En général, n'importe quelle fonction d'appariement peut être utilisée pour résoudre ce problème. Pour chacune de ces méthodes, considérez que le numéro de siège d'un passager sur un autocar est égal à , et que son numéro d'autocar est égal à , et les chiffres et sont ensuite introduits dans les deux arguments de la fonction d'appariement . ${\style d'affichage n}$${\style d'affichage c}$${\style d'affichage n}$${\style d'affichage c}$

Méthode des puissances premières

Videz les chambres impaires en envoyant le client de chambre en chambre , puis mettez le chargement du premier wagon dans les chambres , le chargement du deuxième wagon dans les chambres ; pour le numéro de car nous utilisons les pièces où est le ième nombre premier impair . Cette solution laisse certaines chambres vides (ce qui peut être utile ou non à l'hôtel) ; en particulier, tous les nombres impairs qui ne sont pas des puissances premières , comme 15 ou 847, ne seront plus occupés. (Donc, à proprement parler, cela montre que le nombre d'arrivées est inférieur ou égal au nombre de postes vacants créés. Il est plus facile de montrer, par un moyen indépendant, que le nombre d'arrivées est également supérieur ou égal au nombre de postes vacants, et donc qu'ils sont égaux , que de modifier l'algorithme pour un ajustement exact.) (L'algorithme fonctionne aussi bien si on échange et , mais quel que soit le choix fait, il doit être appliqué uniformément tout au long.) ${\style d'affichage i}$${\style d'affichage 2^{i}}$${\style d'affichage 3^{n}}$${\style d'affichage 5^{n}}$${\style d'affichage c}$${\style d'affichage p^{n}}$${\style d'affichage p}$${\style d'affichage c}$${\style d'affichage n}$${\style d'affichage c}$

Méthode de factorisation en nombres premiers

Vous pouvez mettre chaque personne d'un certain siège et autocar en chambre (en supposant que c =0 pour les personnes déjà à l'hôtel, 1 pour le premier autocar, etc...). Parce que chaque nombre a une factorisation première unique , il est facile de voir que toutes les personnes auront une pièce, alors que deux personnes ne se retrouveront pas dans la même pièce. Par exemple, la personne de la salle 2592 ( ) était assise dans la 4e voiture, sur la 5e place. Comme la méthode des puissances premières, cette solution laisse certaines pièces vides. ${\style d'affichage s}$${\style d'affichage c}$${\displaystyle 2^{s}3^{c}}$${\style d'affichage 2^{5}3^{4}}$

Cette méthode peut aussi facilement être étendue pour des nuits infinies, des entrées infinies, etc... ( ) ${\displaystyle 2^{s}3^{c}5^{n}7^{e}}$

Méthode d'entrelacement

Pour chaque passager, comparez les longueurs de et telles qu'elles sont écrites dans n'importe quel système de numération positionnelle , tel que decimal . (Traitez chaque résident de l'hôtel comme étant dans la voiture n°0.) Si l'un des nombres est plus court, ajoutez-lui des zéros non significatifs jusqu'à ce que les deux valeurs aient le même nombre de chiffres. Entrelacez les chiffres pour produire un numéro de chambre : ses chiffres seront [premier chiffre du numéro de voiture]-[premier chiffre du numéro de siège]-[deuxième chiffre du numéro de voiture]-[deuxième chiffre du numéro de siège]-etc. L'invité de l'hôtel (coach #0) dans la chambre numéro 1729 se déplace vers la chambre 01070209 (c'est-à-dire la chambre 1 070 209). Le passager du siège 1234 de la voiture 789 se rend au local 01728394 (soit le local 1 728 394). ${\style d'affichage n}$${\style d'affichage c}$

Contrairement à la solution Prime Power, celle-ci remplit complètement l'hôtel et nous pouvons reconstituer l'autocar et le siège d'origine d'un client en inversant le processus d'entrelacement. Ajoutez d'abord un zéro non significatif si la pièce comporte un nombre impair de chiffres. Désentrelacez ensuite le numéro en deux chiffres : le numéro de car se compose des chiffres impairs et le numéro de siège est des chiffres pairs. Bien sûr, l'encodage d'origine est arbitraire et les rôles des deux nombres peuvent être inversés (place-impair et coach-pair), tant qu'il est appliqué de manière cohérente.

Méthode des nombres triangulaires

Ceux qui sont déjà à l'hôtel seront déplacés vers la chambre , ou le e numéro triangulaire . Ceux dans une voiture seront dans la chambre , ou le nombre triangulaire plus . De cette façon, toutes les chambres seront occupées par un et un seul invité. ${\style d'affichage (n^{2}+n)/2}$${\style d'affichage n}$${\style d'affichage ((c+n-1)^{2}+c+n-1)/2+n}$${\style d'affichage (c+n-1)}$${\style d'affichage n}$

Cette fonction d'appariement peut être démontrée visuellement en structurant l'hôtel comme une pyramide d' une pièce d'une hauteur infinie . La rangée la plus haute de la pyramide est une pièce simple : pièce 1 ; sa deuxième rangée est les chambres 2 et 3 ; etc. La colonne formée par l'ensemble des pièces les plus à droite correspondra aux nombres triangulaires. Une fois remplies (par les occupants redistribués de l'hôtel), les chambres vides restantes forment une forme de pyramide exactement identique à la forme d'origine. Ainsi, le processus peut être répété pour chaque ensemble infini. Faire celui-ci à la fois pour chaque coach nécessiterait un nombre infini d'étapes, mais en utilisant les formules précédentes, un invité peut déterminer ce que "sera" sa chambre une fois que son coach aura été atteint dans le processus, et pourra simplement s'y rendre. immédiatement.

Méthode de dénombrement arbitraire

Laissez . est dénombrable puisque est dénombrable, nous pouvons donc énumérer ses éléments . Maintenant, si , affectez le e client du e car à la e chambre (considérez les clients déjà dans l'hôtel comme des clients du e car). Ainsi nous avons une fonction affectant chaque personne à une pièce ; de plus, cette affectation ne saute aucune pièce. ${\displaystyle S:=\{(a,b)\mid a,b\in \mathbb {N} \}}$${\style d'affichage S}$${\displaystyle \mathbb {N} }$${\displaystyle s_{1},s_{2},\dots }$${\style d'affichage s_{n}=(a,b)}$${\style d'affichage b}$${\style d'affichage a}$${\style d'affichage n}$${\style d'affichage 0}$

D'autres couches d'infini

Supposons que l'hôtel se trouve à côté d'un océan et qu'un nombre infini de car-ferries arrivent, chacun transportant un nombre infini d'autocars, chacun avec un nombre infini de passagers. C'est une situation impliquant trois "niveaux" d' infini , et elle peut être résolue par des extensions de n'importe laquelle des solutions précédentes.

La méthode de factorisation première peut être appliquée en ajoutant un nouveau nombre premier pour chaque couche supplémentaire d'infini ( , avec le bac). ${\displaystyle 2^{s}3^{c}5^{f}}$${\style d'affichage f}$

La solution de puissance principale peut être appliquée avec une exponentiation supplémentaire des nombres premiers, ce qui entraîne des nombres de pièces très grands même avec de petites entrées. Par exemple, le passager du deuxième siège du troisième bus sur le deuxième ferry (adresse 2-3-2) augmenterait le 2e prime impair (5) à 49, ce qui est le résultat du 3e prime impair (7) étant élevé à la puissance de son numéro de siège (2). Ce numéro de chambre aurait plus de trente chiffres décimaux.

La méthode d'entrelacement peut être utilisée avec trois "brins" entrelacés au lieu de deux. Le passager avec l'adresse 2-3-2 irait à la salle 232, tandis que celui avec l'adresse 4935-198-82217 irait à la salle #008,402,912,391,587 (les zéros de tête peuvent être supprimés).

Anticipant la possibilité d'un nombre illimité de couches d'invités infinis, l'hôtel peut souhaiter attribuer des chambres de telle sorte qu'aucun invité n'ait besoin de déménager, quel que soit le nombre d'invités qui arrivent par la suite. Une solution consiste à convertir l'adresse de chaque arrivée en un nombre binaire dans lequel les uns sont utilisés comme séparateurs au début de chaque couche, tandis qu'un nombre au sein d'une couche donnée (comme le numéro de car d'un invité) est représenté avec autant de zéros. Ainsi, un invité avec l'adresse précédente 2-5-1-3-1 (cinq couches infinies) irait à la salle 10010000010100010 (décimal 295458).

En tant qu'étape supplémentaire dans ce processus, un zéro peut être supprimé de chaque section du numéro ; dans cet exemple, la nouvelle chambre du client est 101000011001 (décimal 2585). Cela garantit que chaque pièce pourrait être occupée par un invité hypothétique. Si aucun groupe infini d'invités n'arrive, seules les pièces qui sont une puissance de deux seront occupées.

Couches infinies de nidification

Bien qu'une pièce puisse être trouvée pour un nombre fini d'infinités de personnes imbriquées, il n'en va pas toujours de même pour un nombre infini de couches, même si un nombre fini d'éléments existe à chaque couche.

Une analyse

Le paradoxe de Hilbert est un paradoxe véridique : il conduit à un résultat contre-intuitif dont la vérité est prouvée . Les déclarations « il y a un invité dans chaque chambre » et « plus aucun invité ne peut être logé » ne sont pas équivalentes lorsqu'il y a une infinité de chambres.

Au départ, cet état de fait peut sembler contre-intuitif. Les propriétés des "collections infinies de choses" sont assez différentes de celles des "collections finies de choses". Le paradoxe du Grand Hôtel de Hilbert peut être compris en utilisant la théorie des nombres transfinis de Cantor . Ainsi, dans un hôtel ordinaire (fini) avec plus d'une chambre, le nombre de chambres impaires est évidemment inférieur au nombre total de chambres. Cependant, dans le bien nommé Grand Hotel de Hilbert, le nombre de chambres impaires n'est pas inférieur au "nombre" total de chambres. En termes mathématiques, la cardinalité du sous - ensemble contenant les pièces impaires est la même que la cardinalité de l' ensemble de toutes les pièces. En effet, les ensembles infinis sont caractérisés comme des ensembles qui ont des sous-ensembles propres de même cardinalité. Pour les ensembles dénombrables (ensembles avec la même cardinalité que les nombres naturels ) cette cardinalité est . ${\displaystyle \aleph _{0}}$

Reformulé, pour tout ensemble dénombrable infini, il existe une fonction bijective qui mappe l'ensemble dénombrable infini à l'ensemble des nombres naturels, même si l'ensemble dénombrable infini contient les nombres naturels. Par exemple, l'ensemble des nombres rationnels - ces nombres qui peuvent être écrits comme un quotient d'entiers - contient les nombres naturels en tant que sous-ensemble, mais n'est pas plus grand que l'ensemble des nombres naturels puisque les rationnels sont dénombrables : il y a une bijection de les naturels aux rationnels.

Références dans la fiction

• BBC Learning Zone a projeté à plusieurs reprises un documentaire éducatif unique en 1996, Hotel Hilbert, situé dans l'hôtel, vu à travers les yeux d'une jeune invitée Fiona Knight, son nom étant un jeu de mots fini. Le programme a été conçu pour éduquer les téléspectateurs sur le concept de l'infini.
• Le roman White Light du mathématicien / écrivain de science-fiction Rudy Rucker comprend un hôtel basé sur le paradoxe de Hilbert, et où le protagoniste de l'histoire rencontre Georg Cantor .
• Le roman de science-fiction de Stephen Baxter , Transcendent, a une brève discussion sur la nature de l'infini, avec une explication basée sur le paradoxe, modifiée pour utiliser des soldats plutôt que des hôtels.
• La nouvelle " Ondulations dans la mer de Dirac " de Geoffrey A. Landis , lauréate du prix Nebula, utilise l'hôtel Hilbert pour expliquer pourquoi une mer de Dirac infiniment pleine peut néanmoins toujours accepter des particules.
• Dans le roman de Peter Høeg , Miss Smilla's Feeling for Snow , l'héroïne titulaire reflète qu'il est admirable que le directeur de l'hôtel et les clients se donnent beaucoup de mal pour que le retardataire puisse avoir sa propre chambre et un peu d'intimité.
• Dans le roman pour enfants d' Ivar Ekeland , Le chat au pays des nombres , un « M. Hilbert » et sa femme dirigent un hôtel infini pour tous les nombres entiers. L'histoire progresse à travers la méthode triangulaire pour les rationnels.
• Dans le roman de Will Wiles The Way Inn , sur un motel infiniment grand, le nom du méchant est Hilbert.
• Dans le roman de Reginald Hill « The Stranger House », le personnage de Sam fait référence au paradoxe de l'hôtel Hilbert.
• La nouvelle de Naum Ya. Vilenkin The Extraordinary Hotel (souvent attribué à tort à Stanislaw Lem ) montre la manière dont le Grand Hôtel de Hilbert peut être remanié lorsque de nouveaux hôtes infinis arrivent.
• John Roderick et Ken Jennings ont discuté de l'hôtel sur leur podcast Omnibus dans l'épisode The Hilbert Hotel Entry .
• La saga de bandes dessinées The Tempest de la série League of Extraordinary Gentlemen d' Alan Moore et Kevin O'Neill montre un méchant appelé Infinity. Dans l'histoire, il est suggéré que le méchant se rend à l'hôtel sur la base du paradoxe de Hilbert. Georg Cantor est également mentionné.

Voir également

• Liste des paradoxes
• Paradoxe Banach-Tarski
• Le paradoxe de Galilée
• Paradoxes de la théorie des ensembles
• Principe du pigeonnier

Les références

• Hilbert, David (2013), Ewald, Guillaume ; Sieg, Wilfried (éd.), David Hilbert's Lectures on the Foundations of Arithmetics and Logic 1917-1933 , Heidelberg : Springer-Verlag, doi : 10.1007/978-3-540-69444-1 , ISBN 978-3-540-20578-4

Liens externes

• Hôtel Hilbert infini . M. Hazewinkel. Encyclopédie des mathématiques , Springer. Consulté le 25 mai 2007.
• Nancy Casey, bienvenue à l'hôtel Infinity !  - Le paradoxe raconté comme un récit humoristique, mettant en vedette un propriétaire d'hôtel et un entrepreneur en bâtiment basé sur les mathématiciens du XIXe siècle en conflit Georg Cantor et Leopold Kronecker
• Steven Strogatz, The Hilbert Hotel , NY Times, 9 mai 2010
• Hilbert's Infinite Hotel , h2g2
• L'Hôtel Hilbert - Présentation YouTube
• "Au-delà du fini"
• voir chanson p. 704 de l'American Mathematical Monthly d'octobre 2006 ou p. 177 du Journal des mathématiques et des arts de décembre 2011
• Le paradoxe de l'hôtel infini - Jeff Dekofsky - Leçons TED-Ed