Méthode de goulot d'étranglement de l'information - Information bottleneck method

La méthode du goulot d'étranglement de l'information est une technique de la théorie de l'information introduite par Naftali Tishby , Fernando C. Pereira et William Bialek . Il est conçu pour trouver le meilleur compromis entre la précision et la complexité ( compression ) lors de la synthèse (par exemple, le regroupement ) d'une variable aléatoire X , étant donné une distribution de probabilité conjointe p(X,Y) entre X et une variable pertinente observée Y - et auto-décrit comme fournissant "un cadre étonnamment riche pour discuter d'une variété de problèmes dans le traitement du signal et l'apprentissage" .

Les applications incluent le regroupement distributionnel et la réduction de dimension , et plus récemment , il a été suggéré comme fondement théorique de l' apprentissage en profondeur . Il généralise la notion classique de minimes statistiques suffisantes à partir des statistiques paramétriques des distributions arbitraires, pas nécessairement la forme exponentielle. Il le fait en assouplissant la condition de suffisance pour capturer une partie de l' information mutuelle avec la variable pertinente Y .

Le goulot d'étranglement de l'information peut également être considéré comme un problème de distorsion de débit , avec une fonction de distorsion qui mesure à quel point Y est prédit à partir d'une représentation compressée T par rapport à sa prédiction directe à partir de X . Cette interprétation fournit un algorithme itératif général pour résoudre le compromis du goulot d'étranglement de l'information et calculer la courbe d'information à partir de la distribution p(X,Y) .

Soit la représentation compressée donnée par une variable aléatoire . L'algorithme minimise la fonctionnelle suivante par rapport à la distribution conditionnelle : ${\style d'affichage T}$${\style d'affichage p(t|x)}$

${\displaystyle \min _{p(t|x)}\,\,I(X;T)-\beta I(T;Y),}$

où et sont les informations mutuelles de et , et de et , respectivement, et est un multiplicateur de Lagrange . ${\style d'affichage I(X;T)}$${\style d'affichage I(T;Y)}$${\style d'affichage X}$${\style d'affichage T}$${\style d'affichage T}$${\style d'affichage Y}$${\displaystyle \beta }$

Statistiques suffisantes minimales

Équations auto-cohérentes

Théorie de l'apprentissage

Transitions de phase

Théorie de l'information de l'apprentissage profond

La théorie des goulots d'étranglement de l'information est récemment utilisée pour étudier les réseaux de neurones profonds (DNN). Considérons et respectivement comme les couches d'entrée et de sortie d'un DNN, et soit n'importe quelle couche cachée du réseau. Shwartz-Ziv et Tishby ont proposé le goulot d'étranglement de l'information qui exprime le compromis entre les mesures d'information mutuelle et . Dans ce cas, et respectivement quantifier la quantité d'informations que la couche cachée contient sur l'entrée et la sortie. Ils ont conjecturé que le processus de formation d'un DNN se compose de deux phases distinctes ; 1) une phase d'ajustement initiale dans laquelle augmente, et 2) une phase de compression ultérieure dans laquelle diminue. Saxe et al. en a contré l'affirmation de Shwartz-Ziv et Tishby, déclarant que ce phénomène de compression dans les DNN n'est pas exhaustif et qu'il dépend de la fonction d'activation particulière. En particulier, ils ont affirmé que la compression ne se produit pas avec les fonctions d'activation de ReLu. Shwartz-Ziv et Tishby ont contesté ces affirmations, arguant que Saxe et al n'avaient pas observé de compression en raison de faibles estimations de l'information mutuelle. Récemment, Noshad et al. ont utilisé un estimateur de taux optimal d'informations mutuelles pour explorer cette controverse, en observant que l'estimateur optimal basé sur le hachage révèle le phénomène de compression dans une plus large gamme de réseaux avec des activations ReLu et maxpooling. D'autre part, récemment Goldfeld et al. ont fait valoir que la compression observée est le résultat de phénomènes géométriques et non de la théorie de l'information, un point de vue qui a également été partagé. ${\style d'affichage X}$${\style d'affichage Y}$${\style d'affichage T}$${\style d'affichage I(X,T)}$${\style d'affichage I(T,Y)}$${\style d'affichage I(X,T)}$${\style d'affichage I(T,Y)}$${\style d'affichage I(T,Y)}$${\style d'affichage I(X,T)}$

Goulot d'étranglement variationnel

goulet d'étranglement gaussien

Le goulot d'étranglement gaussien, à savoir l'application de l'approche du goulot d'étranglement de l'information aux variables gaussiennes, conduit à des solutions liées à l' analyse de corrélation canonique . Supposons que sont conjointement des vecteurs normaux nuls multivariés avec des covariances et qu'il s'agit d'une version compressée de qui doit maintenir une valeur donnée d'information mutuelle avec . On peut montrer que l'optimum est un vecteur normal constitué de combinaisons linéaires des éléments dont la matrice a des lignes orthogonales. ${\style d'affichage X,Y\,}$${\displaystyle \Sigma _{XX},\,\,\Sigma _{YY}}$${\style d'affichage T\,}$${\style d'affichage X\,}$${\style d'affichage Y\,}$${\style d'affichage T\,}$${\style d'affichage X,\,\,T=AX\,}$${\style d'affichage A\,}$

La matrice de projection contient en fait des lignes sélectionnées parmi les vecteurs propres gauches pondérés de la décomposition en valeurs singulières de la matrice (généralement asymétrique) ${\style d'affichage A\,}$${\style d'affichage M\,}$

${\displaystyle \Omega =\Sigma _{X|Y}\Sigma _{XX}^{-1}=I-\Sigma _{XY}\Sigma _{YY}^{-1}\Sigma _{XY }^{T}\Sigma _{XX}^{-1}.\,}$

Définir la décomposition en valeur singulière

${\displaystyle \Omega =U\Lambda V^{T}{\text{ with }}\Lambda =\operatorname {Diag} {\big (}\lambda _{1}\leq \lambda _{2}\cdots \lambda _{N}{\grand )}\,}$

et les valeurs critiques

${\displaystyle \beta _{i}^{C}{\underset {\lambda _{i}<1}{=}}(1-\lambda _{i})^{-1}.\,}$

alors le nombre de vecteurs propres actifs dans la projection, ou ordre d'approximation, est donné par ${\style d'affichage M\,}$

${\displaystyle \beta _{M-1}^{C}<\beta \leq \beta _{M}^{C}}$

Et nous obtenons enfin

${\displaystyle A=[w_{1}U_{1},\dots ,w_{M}U_{M}]^{T}}$

Dans lequel les poids sont donnés par

${\displaystyle w_{i}={\sqrt {(\beta (1-\lambda _{i})/\lambda _{i}r_{i}}}}$

où ${\displaystyle r_{i}=U_{i}^{T}\Sigma _{XX}U_{i}.\,}$

L'application du goulot d'étranglement de l'information gaussien aux séries temporelles (processus) donne des solutions liées au codage prédictif optimal. Cette procédure est formellement équivalente à l' analyse linéaire des caractéristiques lentes.

Les structures temporelles optimales dans les systèmes dynamiques linéaires peuvent être révélées dans ce que l'on appelle le goulot d'étranglement des informations passé-futur, une application de la méthode du goulot d'étranglement aux données échantillonnées non gaussiennes. Le concept, tel qu'il est traité par Creutzig, Tishby et al., n'est pas sans complication car deux phases indépendantes composent l'exercice : d'une part l'estimation des densités de probabilité parent inconnues à partir desquelles les échantillons de données sont tirés et d'autre part l'utilisation de ces densités au sein de le cadre théorique de l'information du goulot d'étranglement.

Estimation de la densité

Étant donné que la méthode du goulot d'étranglement est formulée en termes probabilistes plutôt que statistiques, la densité de probabilité sous-jacente aux points d'échantillonnage doit être estimée. Il s'agit d'un problème bien connu avec plusieurs solutions décrites par Silverman . Dans la présente méthode, les probabilités d'échantillons conjoints sont trouvées en utilisant une méthode de matrice de transition de Markov et cela a une certaine synergie mathématique avec la méthode du goulot d'étranglement elle-même. ${\displaystyle X={x_{i}}\,}$

La métrique de distance augmentant arbitrairement entre toutes les paires d'échantillons et la matrice de distance est . Ensuite, les probabilités de transition entre les paires d'échantillons pour certains doivent être calculées. En traitant les échantillons comme des états, et une version normalisée de comme une matrice de probabilité de transition d'état de Markov, le vecteur des probabilités des « états » après les étapes, conditionné par l'état initial , est . Le vecteur de probabilité d'équilibre donné, de façon habituelle, par le vecteur propre dominant de la matrice qui est indépendant du vecteur d'initialisation . Cette méthode de transition de Markov établit une probabilité aux points de l'échantillon qui est censée être proportionnelle aux densités de probabilités là-bas. ${\style d'affichage f\,}$${\displaystyle d_{i,j}=f{\Grand (}{\Grand |}x_{i}-x_{j}{\Grand |}{\Grand )}}$${\displaystyle P_{i,j}=\exp(-\lambda d_{i,j})\,}$${\style d'affichage \lambda >0\,}$${\style d'affichage P\,}$${\style d'affichage t\,}$${\style d'affichage p(0)\,}$${\style d'affichage p(t)=P^{t}p(0)\,}$${\style d'affichage p(\infty )\,}$${\style d'affichage P\,}$${\style d'affichage p(0)\,}$

D'autres interprétations de l'utilisation des valeurs propres de la matrice de distance sont discutées dans Silverman's Density Estimation for Statistics and Data Analysis . ${\style d'affichage d\,}$

Groupes

Dans l'exemple de clustering souple suivant, le vecteur de référence contient des catégories d'échantillons et la probabilité conjointe est supposée connue. Une grappe souple est définie par sa distribution de probabilité sur les échantillons de données . Tishby et al. a présenté l'ensemble itératif d'équations suivant pour déterminer les clusters qui sont finalement une généralisation de l' algorithme de Blahut-Arimoto , développé dans la théorie de la distorsion de taux . L'application de ce type d'algorithme dans les réseaux de neurones semble provenir d'arguments d'entropie résultant de l'application des distributions de Gibbs dans le recuit déterministe. ${\style d'affichage Y\,}$${\style d'affichage p(X,Y)\,}$${\style d'affichage c_{k}\,}$${\style d'affichage x_{i}:\,\,\,p(c_{k}|x_{i})}$

${\displaystyle {\begin{cases}p(c|x)=Kp(c)\exp {\Big (}-\beta \,D^{KL}{\Big [}p(y|x)\, ||\,p(y|c){\Grand ]}{\Grand )}\\p(y|c)=\textstyle \sum _{x}p(y|x)p(c|x)p (x){\big /}p(c)\\p(c)=\textstyle \sum _{x}p(c|x)p(x)\\\end{cases}}}$

La fonction de chaque ligne de l'itération se développe comme

Ligne 1 : Il s'agit d'un ensemble matriciel de probabilités conditionnelles

${\displaystyle A_{i,j}=p(c_{i}|x_{j})=Kp(c_{i})\exp {\Big (}-\beta \,D^{KL}{\Big [}p(y|x_{j})\,||\,p(y|c_{i}){\Grand ]}{\Grand )}}$

La divergence de Kullback-Leibler entre les vecteurs générés par les données de l'échantillon et ceux générés par son proxy d'information réduit est appliquée pour évaluer la fidélité du vecteur compressé par rapport aux données de référence (ou catégorielles) conformément à l'équation fondamentale du goulot d'étranglement. est la divergence de Kullback-Leibler entre les distributions${\style d'affichage D^{KL}\,}$${\style d'affichage Y\,}$${\style d'affichage x\,}$${\style d'affichage c\,}$${\style d'affichage Y\,}$${\style d'affichage D^{KL}(a||b)\,}$${\style d'affichage a,b\,}$

${\displaystyle D^{KL}(a||b)=\sum _{i}p(a_{i})\log {\Big (}{\frac {p(a_{i})}{p( b_{i})}}{\Grand )}}$

et est une normalisation scalaire. La pondération par l'exposant négatif de la distance signifie que les probabilités des clusters antérieurs sont sous-pondérées sur la ligne 1 lorsque la divergence Kullback-Leibler est grande, ainsi les clusters réussis augmentent en probabilité tandis que ceux qui échouent décroissent. ${\style d'affichage K\,}$

Ligne 2 : Deuxième ensemble matriciel de probabilités conditionnelles. Par définition

${\displaystyle {\begin{aligned}p(y_{i}|c_{k})&=\sum _{j}p(y_{i}|x_{j})p(x_{j}|c_{ k})\\&=\somme _{j}p(y_{i}|x_{j})p(x_{j},c_{k}){\big /}p(c_{k})\ \&=\somme _{j}p(y_{i}|x_{j})p(c_{k}|x_{j})p(x_{j}){\big /}p(c_{k })\\\fin{aligné}}}$

où les identités de Bayes sont utilisées. ${\style d'affichage p(a,b)=p(a|b)p(b)=p(b|a)p(a)\,}$

Ligne 3 : cette ligne trouve la distribution marginale des clusters${\style d'affichage c\,}$

${\displaystyle {\begin{aligned}p(c_{i})&=\sum _{j}p(c_{i},x_{j})&=\sum _{j}p(c_{i} |x_{j})p(x_{j})\end{aligné}}}$

Il s'agit d'un résultat standard.

D'autres entrées de l'algorithme sont la distribution marginale de l'échantillon qui a déjà été déterminée par le vecteur propre dominant de et la fonction de divergence de Kullback-Leibler à valeur matricielle ${\style d'affichage p(x)\,}$${\style d'affichage P\,}$

${\displaystyle D_{i,j}^{KL}=D^{KL}{\Big [}p(y|x_{j})\,||\,p(y|c_{i}){\ Gros gros )}}$

dérivées des espacements des échantillons et des probabilités de transition.

La matrice peut être initialisée de manière aléatoire ou avec une estimation raisonnable, tandis que la matrice n'a pas besoin de valeurs préalables. Bien que l'algorithme converge, plusieurs minima peuvent exister et doivent être résolus. ${\style d'affichage p(y_{i}|c_{j})\,}$${\style d'affichage p(c_{i}|x_{j})\,}$

Définir les contours de décision

Pour catégoriser un nouvel échantillon externe à l'ensemble d'apprentissage , la métrique de distance précédente recherche les probabilités de transition entre et tous les échantillons dans , avec une normalisation. Deuxièmement, appliquez les deux dernières lignes de l'algorithme à 3 lignes pour obtenir les probabilités de cluster et de catégorie conditionnelle. ${\style d'affichage x'\,}$${\style d'affichage X\,}$${\style d'affichage x'\,}$${\style d'affichage X:\,\,}$${\displaystyle {\tilde {p}}(x_{i})=p(x_{i}|x')=\mathrm {K} \exp {\Big (}-\lambda f{\big (}{ \Gros |}x_{i}-x'{\Gros |}{\gros )}{\Gros )}}$${\displaystyle \mathrm {K} \,}$

${\displaystyle {\begin{aligned}&{\tilde {p}}(c_{i})=p(c_{i}|x')=\sum _{j}p(c_{i}|x_{ j})p(x_{j}|x')=\somme _{j}p(c_{i}|x_{j}){\tilde {p}}(x_{j})\\&p(y_ {i}|c_{j})=\somme _{k}p(y_{i}|x_{k})p(c_{j}|x_{k})p(x_{k}|x') /p(c_{j}|x')=\somme _{k}p(y_{i}|x_{k})p(c_{j}|x_{k}){\tilde {p}}( x_{k})/{\tilde {p}}(c_{j})\\\end{aligned}}}$

finalement

${\displaystyle p(y_{i}|x')=\sum _{j}p(y_{i}|c_{j})p(c_{j}|x'))=\sum _{j} p(y_{i}|c_{j}){\tilde {p}}(c_{j})\,}$

Le paramètre doit être surveillé de près car, à mesure qu'il est augmenté à partir de zéro, un nombre croissant de caractéristiques, dans l'espace de probabilité de catégorie, se mettent au point à certains seuils critiques. ${\displaystyle \beta \,}$

Un exemple

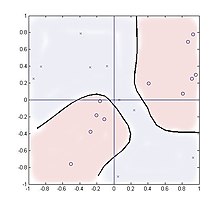
Le cas suivant examine le regroupement dans un multiplicateur à quatre quadrants avec des entrées aléatoires et deux catégories de sortie, , généré par . Cette fonction a deux clusters séparés spatialement pour chaque catégorie et démontre ainsi que la méthode peut gérer de telles distributions. ${\style d'affichage u,v\,}$${\style d'affichage \pm 1\,}$${\displaystyle y=\operatorname {sign} (uv)\,}$

20 échantillons sont prélevés, uniformément répartis sur le carré . Le nombre de clusters utilisés au-delà du nombre de catégories, deux dans ce cas, a peu d'effet sur les performances et les résultats sont affichés pour deux clusters à l'aide de paramètres . ${\style d'affichage [-1,1]^{2}\,}$${\displaystyle \lambda =3,\,\beta =2.5}$

La fonction de distance est où tandis que la distribution conditionnelle est une matrice 2 × 20 ${\displaystyle d_{i,j}={\Grand |}x_{i}-x_{j}{\Grand |}^{2}}$${\displaystyle x_{i}=(u_{i},v_{i})^{T}\,}$${\style d'affichage p(y|x)\,}$

${\displaystyle {\begin{aligned}&Pr(y_{i}=1)=1{\text{ if }}\operatorname {sign} (u_{i}v_{i})=1\,\\&Pr( y_{i}=-1)=1{\text{ if }}\operatorname {sign} (u_{i}v_{i})=-1\,\end{aligned}}}$

et zéro ailleurs.

La sommation de la ligne 2 n'intègre que deux valeurs représentant les valeurs d'apprentissage de +1 ou -1, mais fonctionne néanmoins bien. La figure montre les emplacements des vingt échantillons avec '0' représentant Y = 1 et 'x' représentant Y = -1. Le contour au niveau du rapport de vraisemblance unitaire est montré,

${\displaystyle L={\frac {\Pr(1)}{\Pr(-1)}}=1}$

comme un nouvel échantillon est balayé sur le carré. Théoriquement, le contour doit s'aligner sur les coordonnées et , mais pour de si petits nombres d'échantillons, ils ont plutôt suivi les regroupements parasites des points d'échantillonnage. ${\style d'affichage x'\,}$${\style d'affichage u=0\,}$${\style d'affichage v=0\,}$

Analogies réseau de neurones/logique floue

Cet algorithme est quelque peu analogue à un réseau de neurones avec une seule couche cachée. Les nœuds internes sont représentés par les clusters et les première et deuxième couches de poids de réseau sont les probabilités conditionnelles et respectivement. Cependant, contrairement à un réseau de neurones standard, l'algorithme repose entièrement sur les probabilités comme entrées plutôt que sur les valeurs d'échantillon elles-mêmes, tandis que les valeurs internes et de sortie sont toutes des distributions de densité de probabilité conditionnelles. Les fonctions non linéaires sont encapsulées dans la métrique de distance (ou fonctions d'influence/fonctions à base radiale ) et les probabilités de transition au lieu de fonctions sigmoïdes. ${\style d'affichage c_{j}\,}$${\style d'affichage p(c_{j}|x_{i})\,}$${\style d'affichage p(y_{k}|c_{j})\,}$${\style d'affichage f(.)\,}$

L'algorithme à trois lignes de Blahut-Arimoto converge rapidement, souvent en dizaines d'itérations, et en faisant varier , et et la cardinalité des clusters, divers niveaux de concentration sur les caractéristiques peuvent être atteints. ${\displaystyle \beta \,}$${\style d'affichage \lambda \,}$${\style d'affichage f\,}$

La définition statistique de clustering souple a un certain chevauchement avec le concept d'appartenance verbale floue de la logique floue . ${\style d'affichage p(c_{i}|x_{j})\,}$

Rallonges

Une extension intéressante est le cas du goulot d'étranglement de l'information avec des informations secondaires. Ici, les informations sont maximisées sur une variable cible et minimisées sur une autre, apprenant une représentation informative sur des aspects sélectionnés des données. Officiellement

${\displaystyle \min _{p(t|x)}\,\,I(X;T)-\beta ^{+}I(T;Y^{+})+\beta ^{-}I( T;O^{-})}$

Bibliographie

• Weiss, Y. (1999), « Segmentation using eigenvectors: a unifying view », Actes de la Conférence internationale IEEE sur la vision par ordinateur (PDF) , pp. 975-982
• P. Harremoes et N. Tishby "Le goulot d'étranglement de l'information revisité ou comment choisir une bonne mesure de distorsion". Dans les actes du Symposium international sur la théorie de l'information (ISIT) 2007

Les références