Équation de Langevin - Langevin equation

En physique, une équation de Langevin (du nom de Paul Langevin ) est une équation différentielle stochastique décrivant l'évolution temporelle d'un sous-ensemble des degrés de liberté. Ces degrés de liberté sont généralement des variables collectives (macroscopiques) qui ne changent que lentement par rapport aux autres variables (microscopiques) du système. Les variables rapides (microscopiques) sont responsables de la nature stochastique de l'équation de Langevin. Une application est le mouvement brownien , calculant les statistiques du mouvement aléatoire d'une petite particule dans un fluide en raison de collisions avec les molécules environnantes en mouvement thermique.

Le mouvement brownien comme prototype

L'équation originale de Langevin décrit le mouvement brownien , le mouvement apparemment aléatoire d'une particule dans un fluide dû à des collisions avec les molécules du fluide,

${\displaystyle m{\frac {d\mathbf {v} }{dt}}=-\lambda \mathbf {v} +{\boldsymbol {\eta }}\left(t\right).}$

Les degrés de liberté d'intérêt ici sont la vitesse de la particule, désigne la masse de la particule. La force agissant sur la particule s'écrit comme la somme d'une force visqueuse proportionnelle à la vitesse de la particule ( loi de Stokes ) et d'un terme de bruit (le nom donné dans les contextes physiques aux termes des équations différentielles stochastiques qui sont des processus stochastiques ) représentant le effet des collisions avec les molécules du fluide. La force a une distribution de probabilité gaussienne avec fonction de corrélation ${\displaystyle \mathbf {v} }$${\style d'affichage m}$ ${\displaystyle {\boldsymbol {\eta }}\left(t\right)}$${\displaystyle {\boldsymbol {\eta }}\left(t\right)}$

${\displaystyle \left\langle \eta _{i}\left(t\right)\eta _{j}\left(t^{\prime }\right)\right\rangle =2\lambda k_{B} T\delta _{i,j}\delta \left(tt^{\prime }\right),}$

où est la constante de Boltzmann , est la température et est la ième composante du vecteur . La forme -fonction des corrélations dans le temps signifie que la force à un moment est supposée être complètement non corrélée avec la force à tout autre moment. Ceci est une approximation; la force aléatoire réelle a un temps de corrélation non nul correspondant au temps de collision des molécules. Cependant, l'équation de Langevin est utilisée pour décrire le mouvement d'une particule « macroscopique » à une échelle de temps beaucoup plus longue, et dans cette limite la corrélation et l'équation de Langevin deviennent pratiquement exactes. ${\style d'affichage k_{B}}$${\style d'affichage T}$${\displaystyle \eta _{i}\left(t\right)}$${\displaystyle {\boldsymbol {\eta }}\left(t\right)}$${\style d'affichage \delta }$${\style d'affichage t}$${\style d'affichage \delta }$

Une autre caractéristique prototypique de l'équation de Langevin est l'occurrence du coefficient d'amortissement dans la fonction de corrélation de la force aléatoire, un fait également connu sous le nom de relation d'Einstein . ${\style d'affichage \lambda }$

Aspects mathématiques

Une force fluctuante strictement corrélée n'est pas une fonction au sens mathématique habituel et même la dérivée n'est pas définie dans cette limite. Ce problème disparaît lorsque l'équation de Langevin est écrite sous forme intégrale et une équation de Langevin doit toujours être interprétée comme une abréviation de son intégrale de temps. Le terme mathématique général pour les équations de ce type est « équation différentielle stochastique ». ${\style d'affichage \delta }$${\displaystyle {\boldsymbol {\eta }}\left(t\right)}$${\displaystyle d\mathbf {v} /dt}$${\displaystyle m\mathbf {v} =\int ^{t}\left(-\lambda \mathbf {v} +{\boldsymbol {\eta }}\left(t\right)\right)dt,}$

Une autre ambiguïté mathématique se produit pour les équations de Langevin (plutôt spéciales) avec un bruit multiplicatif, c'est-à-dire des termes comme sur les droites. De telles équations peuvent être interprétées selon le schéma de Stratonovich ou d'Ito, et si la dérivation de l'équation de Langevin ne dit pas laquelle utiliser, cela est de toute façon discutable. Voir Itō calcul . ${\displaystyle |{\boldsymbol {v}}(t)|{\boldsymbol {\eta }}(t)}$

Equation de Langevin générique

Il existe une dérivation formelle d'une équation de Langevin générique de la mécanique classique. Cette équation générique joue un rôle central dans la théorie de la dynamique critique et d'autres domaines de la mécanique statistique hors équilibre. L'équation du mouvement brownien ci-dessus est un cas particulier.

Une condition essentielle de la dérivation est un critère divisant les degrés de liberté en catégories lente et rapide. Par exemple, l'équilibre thermodynamique local dans un liquide est atteint en quelques temps de collision. Mais il faut beaucoup plus de temps pour que les densités de quantités conservées comme la masse et l'énergie se relâchent jusqu'à l'équilibre. Les densités des quantités conservées, et en particulier leurs composantes à grande longueur d'onde, sont donc des candidats variables lentes. Techniquement cette division est réalisée avec l' opérateur de projection Zwanzig , l'outil essentiel dans la dérivation. La dérivation n'est pas complètement rigoureuse du point de vue de la physique mathématique car elle repose sur certaines hypothèses plausibles (semblables aux hypothèses requises ailleurs en mécanique statistique de base), mais est par ailleurs acceptable du point de vue de la physique théorique.

Notons les variables lentes. L'équation générique de Langevin se lit alors ${\displaystyle A=\{A_{i}\}}$

${\displaystyle {\frac {dA_{i}}{dt}}=k_{B}T\sum \limits _{j}{\left[{A_{i},A_{j}}\right]{\ frac {{d}{\mathcal {H}}}{dA_{j}}}}-\sum \limits _{j}{\lambda _{i,j}\left(A\right){\frac { d{\mathcal {H}}}{dA_{j}}}+}\sum \limits _{j}{\frac {d{\lambda _{i,j}\left(A\right)}}{ dA_{j}}}+\eta _{i}\gauche(t\droit).}$

La force fluctuante obéit à une distribution de probabilité gaussienne avec fonction de corrélation ${\displaystyle \eta _{i}\left(t\right)}$

${\displaystyle \left\langle {\eta _{i}\left(t\right)\eta _{j}\left(t^{\prime }\right)}\right\rangle =2\lambda _{ i,j}\left(A\right)\delta \left(tt^{\prime }\right).}$

Ceci implique la relation de réciprocité d'Onsager pour les coefficients d'amortissement . La dépendance de sur est négligeable dans la plupart des cas. Le symbole désigne l'hamiltonien du système, où est la distribution de probabilité d'équilibre des variables . Enfin, est la projection de la fourchette de Poisson des variables lentes et sur l'espace des variables lentes. ${\displaystyle \lambda _{i,j}=\lambda _{j,i}}$${\style d'affichage \lambda }$${\displaystyle d\lambda _{i,j}/dA_{j}}$${\style d'affichage \lambda }$${\style d'affichage A}$${\displaystyle {\mathcal {H}}=-\ln \left(p_{0}\right)}$${\displaystyle p_{0}\gauche(A\droite)}$${\style d'affichage A}$${\style d'affichage [A_{i},A_{j}]}$${\style d'affichage A_{i}}$${\style d'affichage A_{j}}$

Dans le cas du mouvement brownien on aurait , ou et . L'équation du mouvement pour est exacte, il n'y a pas de force fluctuante et pas de coefficient d'amortissement . ${\displaystyle {\mathcal {H}}=\mathbf {p} ^{2}/\left(2mk_{B}T\right)}$${\displaystyle A=\{\mathbf {p} \}}$${\displaystyle A=\{\mathbf {x} ,\mathbf {p} \}}$${\displaystyle [x_{i},p_{j}]=\delta _{i,j}}$${\displaystyle d\mathbf {x} /dt=\mathbf {p} /m}$${\displaystyle \mathbf {x} }$${\displaystyle \eta _{x}}$${\displaystyle \lambda _{x,p}}$

Exemples

Bruit thermique dans une résistance électrique

Circuit électrique composé d'une résistance et d'un condensateur.

Il existe une analogie étroite entre la particule brownienne paradigmatique discutée ci-dessus et le bruit de Johnson , la tension électrique générée par les fluctuations thermiques dans chaque résistance. Le schéma de droite montre un circuit électrique constitué d'une résistance R et d'une capacité C . La variable lente est la tension U entre les extrémités de la résistance. L'hamiltonien lit , et l'équation de Langevin devient ${\displaystyle {\mathcal {H}}=E/k_{B}T=CU^{2}/(2k_{B}T)}$

${\displaystyle {\frac {dU}{dt}}=-{\frac {U}{RC}}+\eta \left(t\right),\;\;\left\langle \eta \left(t \right)\eta \left(t^{\prime }\right)\right\rangle ={\frac {2k_{B}T}{RC^{2}}}\delta \left(tt^{\prime }\droit).}$

Cette équation peut être utilisée pour déterminer la fonction de corrélation

${\displaystyle \left\langle U\left(t\right)U\left(t^{\prime }\right)\right\rangle =\left(k_{B}T/C\right)\exp \left (-\left\vert tt^{\prime }\right\vert /RC\right)\approx 2Rk_{B}T\delta \left(tt^{\prime }\right),}$

qui devient un bruit blanc (bruit de Johnson) lorsque la capacité C devient négligeable.

Dynamique critique

La dynamique du paramètre d'ordre d'une transition de phase de second ordre ralentit près du point critique et peut être décrite avec une équation de Langevin. Le cas le plus simple est la classe d'universalité "modèle A" avec un paramètre d'ordre scalaire non conservé, réalisé par exemple dans des ferroaimants axiaux, ${\displaystyle \varphi }$

${\displaystyle {\begin{aligned}{\frac {\partial \varphi \left(\mathbf {x} ,t\right)}{\partial t}}&=-\lambda {\frac {\delta {\ mathcal {H}}}{\delta \varphi }}+\eta \left(\mathbf {x} ,t\right),\\{\mathcal {H}}&=\int d^{d}x\ gauche[{\frac {1}{2}}r_{0}\varphi ^{2}+u\varphi ^{4}+{\frac {1}{2}}(\nabla \varphi )^{2 }\right],\\\left\langle \eta \left(\mathbf {x} ,t\right)\eta \left(\mathbf {x} ',t'\right)\right\rangle &=2 \lambda \delta \left(\mathbf {x} -\mathbf {x} '\right)\delta \left(t-t'\right).\end{aligned}}}$

D'autres classes d'universalité (la nomenclature est "modèle A",..., "modèle J") contiennent un paramètre d'ordre diffusant, des paramètres d'ordre à plusieurs composantes, d'autres variables critiques et/ou des contributions des parenthèses de Poisson.

Oscillateur harmonique dans un fluide

${\displaystyle m{\frac {dv}{dt}}=-\lambda v+\eta (t)-kx}$

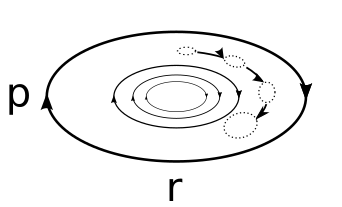
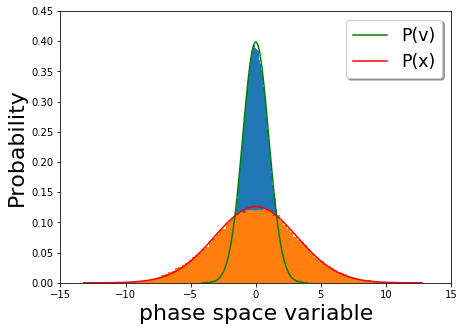
Une particule dans un fluide est également décrite par l'équation de Langevin avec un potentiel, une force d'amortissement et des fluctuations thermiques données par le théorème fluctuation dissipation . Si le potentiel est un potentiel d'oscillateur harmonique, les courbes à énergie constante sont des ellipses, comme le montre la figure 1 ci-dessous. Cependant, en présence d'une force de dissipation, une particule continue de perdre de l'énergie dans l'environnement. D'autre part, la fluctuation thermique ajoute aléatoirement de l'énergie à la particule. En l'absence de fluctuations thermiques, la particule perd continuellement de l'énergie cinétique et le portrait de phase de l'évolution temporelle de la vitesse en fonction de la position ressemble à une ellipse qui s'enroule jusqu'à atteindre une vitesse nulle. A l'inverse, les fluctuations thermiques donnent des coups de pied aux particules qui ne permettent pas à la particule de perdre toute son énergie. Ainsi, aux temps longs, l'ensemble initial d'oscillateurs stochastiques s'étale, pour finalement atteindre l' équilibre thermique , pour lesquels la distribution de vitesse et de position est donnée par la distribution de Maxwell-Boltzmann . Dans le graphique ci-dessous (Figure 2), la distribution de la vitesse à long terme (orange) et les distributions de position (bleu) dans un potentiel harmonique ( ) sont tracées avec les probabilités de Boltzmann pour la vitesse (rouge) et la position (vert). Nous voyons que le comportement tardif représente l'équilibre thermique. ${\displaystyle U={\frac {1}{2}}kx^{2}}$

Trajectoires des particules browniennes libres

Considérons une particule de masse libre avec l'équation du mouvement décrite par ${\style d'affichage m}$

${\displaystyle m{\frac {d\mathbf {v} }{dt}}=-{\frac {\mathbf {v} }{\mu }}+{\boldsymbol {\eta }}(t),}$

où est la vitesse des particules, est la mobilité des particules, et est une force fluctuant rapidement dont la moyenne temporelle s'annule sur une échelle de temps caractéristique des collisions de particules, c'est-à-dire . La solution générale de l'équation du mouvement est ${\displaystyle \mathbf {v} =d\mathbf {r} /dt}$${\style d'affichage \mu }$${\displaystyle {\boldsymbol {\eta }}(t)=m\mathbf {a} (t)}$${\style d'affichage t_{c}}$${\displaystyle {\overline {{\boldsymbol {\eta }}(t)}}=0}$

${\displaystyle \mathbf {v} (t)=\mathbf {v} (0)e^{-t/\tau }+\int _{0}^{t}\mathbf {a} (t')e ^{-(t-t')/\tau }dt',}$

où est le temps de relaxation du mouvement brownien. Comme prévu par la nature aléatoire du mouvement brownien, la vitesse de dérive moyenne décroît rapidement jusqu'à zéro à . On peut aussi montrer que la fonction d'autocorrélation de la vitesse des particules est donnée par ${\displaystyle \tau =m\mu }$${\displaystyle \langle \mathbf {v} (t)\rangle =\mathbf {v} (0)e^{-t/\tau }}$${\style d'affichage t\gg \tau }$${\displaystyle \mathbf {v} }$

Déplacements au carré simulés de particules browniennes libres (lignes ondulées semi-transparentes) en fonction du temps, pour trois choix sélectionnés de vitesse au carré initiale qui sont respectivement 0, 3kT/m et 6kT/m, 3kT/m étant la valeur d'équipartition en équilibre thermique. Les courbes pleines colorées indiquent les déplacements quadratiques moyens pour les choix de paramètres correspondants.

${\displaystyle {\begin{aligned}R_{vv}(t_{1},t_{2})&\equiv \langle \mathbf {v} (t_{1})\cdot \mathbf {v} (t_{ 2})\rangle \\&=v^{2}(0)e^{-(t_{1}+t_{2})/\tau }+\int _{0}^{t_{1}} \int _{0}^{t_{2}}R_{aa}(t_{1}',t_{2}')e^{-(t_{1}+t_{2}-t_{1}' -t_{2}')/\tau }dt_{1}'dt_{2}'\\&\simeq v^{2}(0)e^{-|t_{2}-t_{1}|/ \tau }+{\bigg [}{\frac {3k_{B}T}{m}}-v^{2}(0){\bigg ]}{\Big [}e^{-|t_{2 }-t_{1}|/\tau }-e^{-(t_{1}+t_{2})/\tau }{\Big ]},\end{aligned}}}$

où nous avons utilisé la propriété que les variables et deviennent non corrélées pour les séparations temporelles . En outre, la valeur de est fixée à telle qu'elle obéit au théorème d'équipartition . Notez que si le système est initialement à l'équilibre thermique déjà avec , alors pour tout , ce qui signifie que le système reste à l'équilibre à tout moment. ${\displaystyle \mathbf {a} (t_{1}')}$${\displaystyle \mathbf {a} (t_{2}')}$${\displaystyle t_{2}'-t_{1}'\gg t_{c}}$${\displaystyle \lim _{t\to \infty }\langle v^{2}(t)\rangle =\lim _{t\to \infty }R_{vv}(t,t)}$${\displaystyle 3k_{B}T/m}$${\style d'affichage v^{2}(0)=3k_{B}T/m}$${\displaystyle \langle v^{2}(t)\rangle =3k_{B}T/m}$${\style d'affichage t}$

La vitesse de la particule brownienne peut être intégrée pour donner sa trajectoire (en supposant qu'elle soit initialement à l'origine) ${\displaystyle \mathbf {v} (t)}$

${\displaystyle \mathbf {r} (t)=\mathbf {v} (0)\tau {\big (}1-e^{-t/\tau }{\big )}+\tau \int _{ 0}^{t}\mathbf {a} (t'){\Big [}1-e^{-(t-t')/\tau }{\Big ]}dt'.}$

Par conséquent, le déplacement moyen résultant est asymptote au fur et à mesure que le système se détend et que le hasard prend le dessus. De plus, le déplacement quadratique moyen peut être déterminé de la même manière que le calcul précédent pour être ${\displaystyle \langle \mathbf {r} (t)\rangle =\mathbf {v} (0)\tau {\big (}1-e^{-t/\tau }{\big )}}$${\displaystyle \mathbf {v} (0)\tau }$

${\displaystyle \langle r^{2}(t)\rangle =v^{2}(0)\tau ^{2}{\big (}1-e^{-t/\tau }{\big ) }^{2}-{\frac {3k_{B}T}{m}}\tau ^{2}{\big (}1-e^{-t/\tau }{\big )}{\big (}3-e^{-t/\tau }{\big )}+{\frac {6k_{B}T}{m}}\tau t.}$

On peut voir que , indiquant que le mouvement des particules browniennes à des échelles de temps beaucoup plus courtes que le temps de relaxation du système est (approximativement) invariant par inversion du temps . D'autre part, , ce qui suggère que le mouvement aléatoire à long terme des particules browniennes est un processus dissipatif irréversible . Ici, nous avons utilisé la relation d'Einstein-Smoluchowski , où est le coefficient de diffusion du fluide. ${\displaystyle \langle r^{2}(t\ll \tau )\rangle \simeq v^{2}(0)t^{2}}$${\style d'affichage \tau }$${\displaystyle \langle r^{2}(t\gg \tau )\rangle \simeq 6k_{B}T\tau t/m=6\mu k_{B}Tt=6Dt}$ ${\displaystyle D={\mu \,k_{B}T}}$${\style d'affichage D}$

Ce tracé correspond aux solutions de l'équation de Langevin complète obtenue par la méthode d'Euler-Maruyama . Le panneau de gauche montre l'évolution temporelle du portrait de phase d'un oscillateur harmonique à différentes températures. Le panneau de droite capture les distributions de probabilité d'équilibre correspondantes. À température nulle, la vitesse décroît rapidement de sa valeur initiale (le point rouge) à zéro en raison de l'amortissement. Pour des températures non nulles, la vitesse peut être ramenée à des valeurs supérieures à la valeur initiale en raison des fluctuations thermiques. Aux temps longs, la vitesse reste non nulle, et les distributions de position et de vitesse correspondent à celle de l'équilibre thermique.

Récupération des statistiques de Boltzmann

Les équations de Langevin pour un système dans lequel chaque particule est affectée par une force externe et aussi des collisions aléatoires avec d'autres particules doivent reproduire la distribution de Boltzmann , qui est la fonction de distribution de probabilité pour les particules en équilibre thermique. C'est le mouvement brownien en présence d'un forçage externe. Le cas sur- amorti est réalisé lorsque l'inertie de la particule est négligeable par rapport à la force d'amortissement. La trajectoire de la particule dans un potentiel est décrite par l'équation de Langevin suramortie ${\displaystyle F=-{\partial V/\partial x}}$${\style d'affichage x(t)}$${\style d'affichage V(x)}$

${\displaystyle \lambda {\frac {dx}{dt}}=-{\frac {\partial V(x)}{\partial x}}+\eta (t)\equiv -{\frac {\partial V (x)}{\partial x}}+{\sqrt {2}lambda k_{B}T}}{dB_{t} \over dt},}$

où le bruit est caractérisé par le bruit blanc , ou de manière équivalente en termes de processus de Wiener , et est la constante d'amortissement. Nous souhaitons calculer la distribution de la position de la particule au cours du temps. Un moyen direct de déterminer cette distribution est d'introduire une fonction de test , et de regarder la moyenne de cette fonction sur toutes les réalisations (moyenne d'ensemble) qui devrait disparaître, ${\displaystyle \left\langle \eta (t)\eta (t')\right\rangle =2k_{B}T\lambda \delta (t-t')}$${\style d'affichage B_{t}}$${\style d'affichage \lambda }$${\style d'affichage p(x)}$${\style d'affichage f}$

${\displaystyle {\frac {d\left\langle f(x(t))\right\rangle }{dt}}=0,}$

parce que la moyenne de devrait être indépendante du temps pour fini . Maintenant, d'après le lemme d' Itô pour le processus de dérive-diffusion d'Itô X _t satisfaisant l' équation différentielle stochastique , la différentielle d'une fonction deux fois différentiable f ( t , x ) est donnée par ${\style d'affichage f(x(t))}$${\style d'affichage x(t)}$ ${\displaystyle dX_{t}=\mu _{t}\,dt+\sigma _{t}\,dB_{t}}$

${\displaystyle df=\left({\frac {\partial f}{\partial t}}+\mu _{t}{\frac {\partial f}{\partial x}}+{\frac {\sigma _{t}^{2}}{2}}{\frac {\partial ^{2}f}{\partial x^{2}}}\right)dt+\sigma _{t}{\frac {\ partiel f}{\partiel x}}\,dB_{t}.}$

En appliquant ceci au calcul ci-dessus, et en considérant que ce n'est pas une fonction explicite du temps, c'est-à-dire , on obtient ${\style d'affichage f(x(t))}$${\displaystyle \partial f/\partial t=0}$

${\displaystyle \left\langle -f'(x){\frac {\partial V}{\partial x}}+k_{B}Tf''(x)\right\rangle =0.}$

Cette moyenne peut être écrite en utilisant la fonction de densité de probabilité ; ${\style d'affichage p(x)}$

${\displaystyle \int \left(-f'(x){\frac {\partial V}{\partial x}}p(x)+{k_{B}T}f''(x)p(x) \right)dx=\int \left(-f'(x){\frac {\partial V}{\partial x}}p(x)-{k_{B}T}f'(x)p'( x)\droit)dx=0,}$

où le second terme a été intégré par parties (d'où le signe négatif). Puisque cela est vrai pour les fonctions arbitraires , nous devons avoir : ${\style d'affichage f}$

${\displaystyle {\frac {\partial V}{\partial x}}p(x)+{k_{B}T}p'(x)=0,}$

récupérant ainsi la distribution de Boltzmann

${\displaystyle p(x)\propto \exp \left({-{\frac {V(x)}{k_{B}T}}}\right).}$

Techniques équivalentes

Une solution d'une équation de Langevin pour une réalisation particulière de la force fluctuante n'a aucun intérêt en soi ; ce qui est intéressant, ce sont les fonctions de corrélation des variables lentes après moyennage sur la force fluctuante. De telles fonctions de corrélation peuvent également être déterminées avec d'autres techniques (équivalentes).

Équation de Fokker-Planck

Une équation de Fokker-Planck est une équation déterministe pour la densité de probabilité dépendante du temps des variables stochastiques . L'équation de Fokker-Planck correspondant à l'équation générique de Langevin ci-dessus peut être dérivée avec des techniques standards (voir par exemple réf.), ${\style d'affichage P\gauche(A,t\droite)}$${\style d'affichage A}$

${\displaystyle {\frac {\partial P\left(A,t\right)}{\partial t}}=\sum _{i,j}{\frac {\partial }{\partial A_{i}} }\left(-k_{B}T\left[A_{i},A_{j}\right]{\frac {\partial {\mathcal {H}}}{\partial A_{j}}}+\ lambda _{i,j}{\frac {\partial {\mathcal {H}}}{\partial A_{j}}}+\lambda _{i,j}{\frac {\partial }{\partial A_ {j}}}\droite)P\gauche(A,t\droite).}$

La distribution d'équilibre est une solution stationnaire. ${\displaystyle P(A)=p_{0}(A)={\text{const}}\times \exp(-{\mathcal {H}})}$

Intégrale de chemin

Une intégrale de chemin équivalente à une équation de Langevin peut être obtenue à partir de l' équation de Fokker-Planck correspondante ou en transformant la distribution de probabilité gaussienne de la force fluctuante en une distribution de probabilité des variables lentes, schématiquement . Le déterminant fonctionnel et les subtilités mathématiques associées disparaissent si l'équation de Langevin est discrétisée de manière naturelle (causale), où dépend de mais pas de . Il s'avère pratique d'introduire des variables de réponse auxiliaires . L'intégrale de chemin équivalente à l'équation générique de Langevin se lit alors ${\displaystyle P^{(\eta )}(\eta )d\eta }$${\style d'affichage \eta }$${\displaystyle P(A)dA=P^{(\eta )}(\eta (A))\det(d\eta /dA)dA}$${\style d'affichage A(t+\Delta t)-A(t)}$${\style d'affichage A(t)}$${\style d'affichage A(t+\Delta t)}$ ${\displaystyle {\tilde {A}}}$

${\displaystyle \int P(A,{\tilde {A}})\,dA\,d{\tilde {A}}=N\int \exp \left(L(A,{\tilde {A}} )\right)dA\,d{\tilde {A}},}$

où est un facteur de normalisation et ${\style d'affichage N}$

${\displaystyle L(A,{\tilde {A}})=\int \sum _{i,j}\left\{{\tilde {A}}_{i}\lambda _{i,j}{ \tilde {A}}_{j}-{\widetilde {A}}_{i}\left\{\delta _{i,j}{\frac {dA_{j}}{dt}}-k_{ B}T\gauche[A_{i},A_{j}\right]{\frac {d{\mathcal {H}}}{dA_{j}}}+\lambda _{i,j}{\frac {d{\mathcal {H}}}{dA_{j}}}-{\frac {d\lambda _{i,j}}{dA_{j}}}\right\}\right\}dt.}$

La formulation intégrale de chemin n'ajoute rien de nouveau, mais elle permet l'utilisation d'outils issus de la théorie quantique des champs ; par exemple, les méthodes de groupe de perturbation et de renormalisation (si elles ont du sens).

Voir également

• Dynamique Langevin

Les références

Lectures complémentaires

• WT Coffey ( Trinity College, Dublin , Irlande) et Yu P. Kalmykov ( Université de Perpignan , France , The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering (Troisième édition), World Scientific Series in Contemporary Chemical Physics - Tome 27.
• Reif, F. Fundamentals of Statistical and Thermal Physics , McGraw Hill New York, 1965. Voir la section 15.5 Équation de Langevin
• R. Friedrich, J. Peinke et Ch. Renner. Comment quantifier les influences déterministes et aléatoires sur les statistiques du marché des changes , Phys. Rév. Lett. 84, 5224 - 5227 (2000)
• LCG Rogers et D. Williams. Diffusions, Markov Processes, and Martingales , Cambridge Mathematical Library, Cambridge University Press, Cambridge, réimpression de la 2e édition (1994), 2000.