Lemme de pompage pour les langages réguliers - Pumping lemma for regular languages

Dans la théorie des langages formels , le lemme de pompage pour les langages réguliers est un lemme qui décrit une propriété essentielle de tous les langages réguliers . De manière informelle, il dit que toutes les chaînes suffisamment longues dans un langage régulier peuvent être pompées - c'est-à-dire avoir une section médiane de la chaîne répétée un nombre arbitraire de fois - pour produire une nouvelle chaîne qui fait également partie du langage.

Plus précisément, le lemme de pompage dit que , pour tout langage régulier il existe une constante de telle sorte que toute chaîne dans une longueur au moins peut être divisé en trois sous - chaînes , et ( avec étant non vide), de telle sorte que les cordes construites en répétant zéro ou plus de temps sont encore dedans . Ce processus de répétition est connu sous le nom de "pompage". De plus, le lemme de pompage garantit que la longueur de sera au plus , imposant une limite aux manières dont il peut être dédoublé. Les langages finis satisfont videment le lemme de pompage en ayant une longueur de chaîne égale à plus un. ${\style d'affichage L}$${\style d'affichage p}$${\style d'affichage w}$${\style d'affichage L}$${\style d'affichage p}$${\style d'affichage x}$${\style d'affichage y}$${\style d'affichage z}$${\style d'affichage w=xyz}$${\style d'affichage y}$${\style d'affichage xz,xyz,xyyz,xyyyz,...}$${\style d'affichage y}$${\style d'affichage L}$${\style d'affichage xy}$${\style d'affichage p}$${\style d'affichage w}$${\style d'affichage p}$${\style d'affichage L}$

Le lemme de pompage est utile pour réfuter la régularité d'une langue spécifique en question. Il a été prouvé pour la première fois par Michael Rabin et Dana Scott en 1959, et redécouvert peu de temps après par Yehoshua Bar-Hillel , Micha A. Perles et Eli Shamir en 1961, en tant que simplification de leur lemme de pompage pour les langues sans contexte .

Déclaration formelle

Soit un langage régulier. Ensuite , il existe un entier dépendant uniquement de telle sorte que chaque chaîne en longueur au moins ( est appelée la « longueur de pompage ») peut être écrit (c. -à- peut être divisé en trois sous - chaînes), satisfaisant aux conditions suivantes: ${\style d'affichage L}$${\style d'affichage p\geq 1}$${\style d'affichage L}$${\style d'affichage w}$${\style d'affichage L}$${\style d'affichage p}$${\style d'affichage p}$${\style d'affichage w=xyz}$${\style d'affichage w}$

• ${\displaystyle |y|\geq 1}$
• ${\style d'affichage |xy|\leq p}$
• ${\displaystyle (\forall n\geq 0)(xy^{n}z\in L)}$

${\style d'affichage y}$est la sous-chaîne qui peut être pompée (supprimée ou répétée un certain nombre de fois, et la chaîne résultante est toujours dans ). (1) signifie que la boucle à pomper doit avoir une longueur d'au moins un ; (2) signifie que la boucle doit se produire dans les premiers caractères. doit être plus petit que (conclusion de (1) et (2)), mais à part cela, il n'y a aucune restriction sur et . ${\style d'affichage L}$${\style d'affichage y}$${\style d'affichage p}$${\style d'affichage |x|}$${\style d'affichage p}$${\style d'affichage x}$${\style d'affichage z}$

En termes simples, pour tout langage régulier , toute chaîne suffisamment longue (en ) peut être divisée en 3 parties. c'est-à - dire de telle sorte que toutes les chaînes pour soient également dans . ${\style d'affichage L}$${\style d'affichage w}$${\style d'affichage L}$${\style d'affichage w=xyz}$${\style d'affichage xy^{n}z}$${\style d'affichage n\geq 0}$${\style d'affichage L}$

Vous trouverez ci-dessous une expression formelle du lemme de pompage.

${\displaystyle {\begin{array}{l}(\forall L\subseteq \Sigma ^{*})\\\quad ({\mbox{regular}}(L)\Rightarrow \\\quad ((\exists p\geq 1)((\forall w\in L)((|w|\geq p)\Rightarrow \\\quad ((\exists x,y,z\in \Sigma ^{*})(w= xyz\land (|y|\geq 1\land |xy|\leq p\land (\forall n\geq 0)(xy^{n}z\in L)))))))))\end{array }}}$

Utilisation du lemme

Le lemme de pompage est souvent utilisé pour prouver qu'un langage particulier n'est pas régulier : une preuve par contradiction peut consister à présenter une chaîne (de la longueur requise) dans le langage qui n'a pas la propriété décrite dans le lemme de pompage.

Par exemple, la langue sur l'alphabet peut être montrée comme non régulière comme suit : ${\displaystyle L=\{a^{n}b^{n}:n\geq 0\}}$${\displaystyle \Sigma =\{a,b\}}$

Soit , et soit comme utilisé dans la déclaration formelle pour le lemme de pompage ci-dessus. Supposons qu'il existe une constante comme l'exige le lemme. Soit in donné par , qui est une chaîne plus longue que . Par le lemme de pompage, il doit exister une décomposition avec et telle que dans pour chaque . Depuis , la chaîne se compose uniquement d'instances de . De plus, parce que , il contient au moins une instance de la lettre . Cependant, a plus d'instances de la lettre que de la lettre , car certaines instances de mais aucune de n'ont été ajoutées. Par conséquent, n'est pas dans ce qui contredit le lemme de pompage. Par conséquent, ne peut pas être régulier. ${\style d'affichage w,x,y,z,p}$${\style d'affichage n}$${\style d'affichage p}$${\style d'affichage w}$${\style d'affichage L}$${\displaystyle w=a^{p}b^{p}}$${\style d'affichage p}$${\style d'affichage w=xyz}$${\style d'affichage |xy|\leq p}$${\displaystyle |y|\geq 1}$${\style d'affichage xy^{i}z}$${\style d'affichage L}$${\style d'affichage i\geq 0}$${\style d'affichage |xy|\leq p}$${\style d'affichage y}$${\style d'affichage a}$${\displaystyle |y|\geq 1}$${\style d'affichage a}$${\style d'affichage xy^{2}z}$${\style d'affichage a}$${\style d'affichage b}$${\style d'affichage a}$${\style d'affichage b}$${\style d'affichage xy^{2}z}$${\style d'affichage L}$${\style d'affichage L}$

La preuve que le langage des parenthèses équilibrées (c'est-à-dire correctement imbriquées) n'est pas régulier suit la même idée. Étant donné , il existe une chaîne de parenthèses équilibrées qui commence par plus que des parenthèses gauches, de sorte qu'elle sera entièrement composée de parenthèses gauches. En répétant , une chaîne peut être produite qui ne contient pas le même nombre de parenthèses gauche et droite, et donc elles ne peuvent pas être équilibrées. ${\style d'affichage p}$${\style d'affichage p}$${\style d'affichage y}$${\style d'affichage y}$

Preuve du lemme de pompage

Idée de preuve : chaque fois qu'une chaîne xyz suffisamment longue est reconnue par un automate fini , elle doit avoir atteint un état ( ) deux fois. Par conséquent, après avoir répété ("pompage") la partie médiane arbitrairement souvent ( xyyz , xyyyz , ...) la chaîne sera toujours reconnue.${\displaystyle q_{s}=q_{t}}$${\style d'affichage y}$

Pour chaque langage régulier, il existe un automate à états finis (FSA) qui accepte le langage. Le nombre d'états dans une telle FSA est compté et ce nombre est utilisé comme longueur de pompage . Pour une chaîne de longueur au moins , soit l'état de départ et soit la séquence des prochains états visités au fur et à mesure de l'émission de la chaîne. Étant donné que la FSA n'a que des états, dans cette séquence d' états visités, il doit y avoir au moins un état qui se répète. Écrivez pour un tel état. Les transitions qui amènent la machine de la première rencontre d'état à la seconde rencontre d'état correspondent à une chaîne. Cette chaîne est appelée dans le lemme, et puisque la machine trouvera une chaîne sans la portion, ou avec la chaîne répétée un nombre quelconque de fois, les conditions du lemme sont satisfaites. ${\style d'affichage p}$${\style d'affichage p}$${\displaystyle q_{0}}$${\displaystyle q_{1},...,q_{p}}$${\style d'affichage p}$${\style d'affichage p}$${\style d'affichage p+1}$${\displaystyle q_{s}}$${\displaystyle q_{s}}$${\displaystyle q_{s}}$${\style d'affichage y}$${\style d'affichage y}$${\style d'affichage y}$

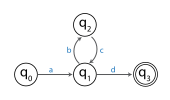
Par exemple, l'image suivante montre un FSA.

Le FSA accepte la chaîne : abcd . Étant donné que cette chaîne a une longueur au moins aussi grande que le nombre d'états, qui est de quatre, le principe du pigeonnier indique qu'il doit y avoir au moins un état répété parmi l'état de départ et les quatre états visités suivants. Dans cet exemple, seul est un état répété. Étant donné que la sous-chaîne bc fait traverser à la machine des transitions qui commencent à l'état et se terminent à l'état , cette partie pourrait être répétée et la FSA accepterait toujours, en donnant la chaîne abcbcd . Alternativement, la partie bc pourrait être supprimée et la FSA accepterait toujours de donner la chaîne ad . En termes de lemme de pompage, la chaîne abcd est divisée en une partie a , une partie bc et une partie d . ${\displaystyle q_{1}}$${\displaystyle q_{1}}$${\displaystyle q_{1}}$${\style d'affichage x}$${\style d'affichage y}$${\style d'affichage z}$

En remarque, le problème de vérifier si une chaîne donnée peut être acceptée par un automate fini non déterministe donné sans visiter un état à plusieurs reprises, est NP difficile .

Version générale du lemme de pompage pour les langues régulières

Si une langue est régulière, alors il existe un certain nombre (la longueur de pompage) de telle sorte que chaque chaîne en avec peut être écrit sous la forme ${\style d'affichage L}$${\style d'affichage p\geq 1}$${\displaystyle uwv}$${\style d'affichage L}$${\style d'affichage |w|\geq p}$

${\style d'affichage uwv=uxyzv}$

avec des chaînes , et tel que , et ${\style d'affichage x}$${\style d'affichage y}$${\style d'affichage z}$${\style d'affichage |xy|\leq p}$${\displaystyle |y|\geq 1}$

${\displaystyle uxy^{i}zv}$est dans pour chaque entier .${\style d'affichage L}$${\style d'affichage i\geq 0}$

À partir de là, la version standard ci - dessus suit un cas particulier, les deux et étant la chaîne vide. ${\displaystyle u}$${\style d'affichage v}$

Étant donné que la version générale impose des exigences plus strictes à la langue, elle peut être utilisée pour prouver la non-régularité de nombreuses autres langues, telles que . ${\displaystyle \{a^{m}b^{n}c^{n}:m\geq 1{\text{ et }}n\geq 1\}}$

L'inverse du lemme n'est pas vrai

Alors que le lemme de pompage déclare que tous les langages réguliers satisfont aux conditions décrites ci-dessus, l'inverse de cette déclaration n'est pas vrai : un langage qui satisfait ces conditions peut toujours être non régulier. En d' autres termes, l'original et la version générale du pompage Lemme donner un nécessaire mais pas suffisante état d'une langue à être régulière.

Par exemple, considérons le langage suivant :

${\displaystyle {\begin{matrice}L&=&\{uvwxy:u,y\in \{0,1,2,3\}^{*};v,w,x\in \{0,1, 2,3\}\land (v=w\lor v=x\lor x=w)\}\\&&\cup \ \{w:w\in \{0,1,2,3\}^{ *}\land {\text{précisément }}{\tfrac {1}{7}}{\text{ des caractères dans }}w{\text{ sont des 3}}\}\end{matrix}}}$.

En d'autres termes, contient toutes les chaînes sur l'alphabet avec une sous-chaîne de longueur 3 comprenant un caractère en double, ainsi que toutes les chaînes sur cet alphabet où précisément 1/7 des caractères de la chaîne sont des 3. Ce langage n'est pas régulier mais peut toujours être "pompé" avec . Supposons qu'une chaîne s ait une longueur d'au moins 5. Ensuite, puisque l'alphabet n'a que quatre caractères, au moins deux des cinq premiers caractères de la chaîne doivent être des doublons. Ils sont séparés par au plus trois caractères. ${\style d'affichage L}$${\style d'affichage \{0,1,2,3\}}$${\style d'affichage p=5}$

• Si les caractères en double sont séparés par 0 ou 1, pompez l'un des deux autres caractères de la chaîne, ce qui n'affectera pas la sous-chaîne contenant les doublons.
• Si les caractères en double sont séparés par 2 ou 3 caractères, pompez 2 des caractères les séparant. Le pompage vers le bas ou vers le haut entraîne la création d'une sous-chaîne de taille 3 qui contient 2 caractères en double.
• La deuxième condition de s'assure que n'est pas régulier : Considérez la chaîne . Cette chaîne est exactement quand et n'est donc pas régulière par le théorème de Myhill-Nerode .${\style d'affichage L}$${\style d'affichage L}$${\style d'affichage (013)^{3m}(012)^{i}}$${\style d'affichage L}$${\style d'affichage i=4m}$${\style d'affichage L}$

Le théorème de Myhill-Nerode fournit un test qui caractérise exactement les langages réguliers. La méthode typique pour prouver qu'un langage est régulier consiste à construire soit une machine à états finis, soit une expression régulière pour le langage.

Voir également

• Lemme d'Ogden
• Lemme de pompage pour les langues sans contexte
• Lemme de pompage pour les langages arborescents réguliers

Remarques

Les références

• Lawson, Mark V. (2004). Automates finis . Chapman et Hall/CRC. ISBN 978-1-58488-255-8. Zbl  1086.68074 .
• Sipser, Michael (1997). "1.4: Langues non régulières". Introduction à la théorie du calcul . Éditions PWS. p.  77-83 . ISBN 978-0-534-94728-6. Zbl  1169.68300 .
• Hopcroft, John E. ; Ullman, Jeffrey D. (1979). Introduction à la théorie des automates, aux langages et au calcul . Reading, Massachusetts : Éditions Addison-Wesley. ISBN 978-0-201-02988-8. Zbl  0426.68001 . (Voir chapitre 3.)
• Bakhadyr Khoussanov ; Anil Nérode (6 décembre 2012). La théorie des automates et ses applications . Springer Science & Business Media. ISBN 978-1-4612-0171-7.