Indicatrice de Tissot - Tissot's indicatrix

En cartographie , une indicatrice de Tissot ( Tissot indicatrix , Tissot's ellipse , Tissot ellipse , ellipse of distorsion ) (pluriel: "Tissot's indicatrices") est un artifice mathématique présenté par le mathématicien français Nicolas Auguste Tissot afin de caractériser les distorsions locales en 1859 et 1871 à la projection cartographique . C'est la géométrie qui résulte de la projection d' un cercle de rayon infinitésimal à partir d'un modèle géométrique courbe, tel qu'un globe, sur une carte. Tissot a prouvé que le diagramme résultant est une ellipse dont les axes indiquent les deux directions principales le long desquelles l'échelle est maximale et minimale en ce point de la carte.

Une seule indicatrice décrit la distorsion en un seul point. Étant donné que la distorsion varie sur une carte, les indicatrices de Tissot sont généralement placées sur une carte pour illustrer le changement spatial de la distorsion. Un schéma commun les place à chaque intersection des méridiens et des parallèles affichés. Ces schémas sont importants dans l'étude des projections cartographiques, à la fois pour illustrer la distorsion et pour fournir la base des calculs qui représentent précisément l'ampleur de la distorsion en chaque point.

Il existe une correspondance biunivoque entre l'indicateur de Tissot et le tenseur métrique de la conversion des coordonnées de la projection cartographique.

La description

La théorie de Tissot a été développée dans le cadre de l' analyse cartographique . Généralement le modèle géométrique représente la Terre, et se présente sous la forme d'une sphère ou d'un ellipsoïde .

Les indicatrices de Tissot illustrent les distorsions linéaires, angulaires et surfaciques des cartes :

• Une carte déforme les distances (distorsion linéaire) chaque fois que le quotient entre les longueurs d'une ligne infiniment courte telle qu'elle est projetée sur la surface de projection, et telle qu'elle est à l'origine sur le modèle terrestre, s'écarte de 1. Le quotient est appelé facteur d'échelle . À moins que la projection ne soit conforme au point considéré, le facteur d'échelle varie selon la direction autour du point.
• Une carte déforme les angles partout où les angles mesurés sur le modèle de la Terre ne sont pas conservés dans la projection. Ceci s'exprime par une ellipse de distorsion qui n'est pas un cercle.
• Une carte déforme les zones là où les zones mesurées dans le modèle de la Terre ne sont pas conservées dans la projection. Ceci est exprimé par des ellipses de distorsion dont les zones varient sur la carte.

Dans les cartes conformes, où chaque point conserve les angles projetés à partir du modèle géométrique, les indicatrices de Tissot sont tous des cercles de taille variant selon l'emplacement, éventuellement aussi avec une orientation variable (étant donné les quatre quadrants du cercle divisés par les méridiens et les parallèles ). Dans les projections à surface égale , où les proportions de surface entre les objets sont conservées, les indicatrices de Tissot ont toutes la même surface, bien que leurs formes et orientations varient avec l'emplacement. Dans les projections arbitraires, la zone et la forme varient sur la carte.

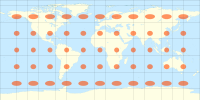
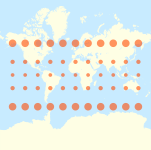
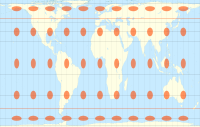
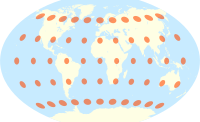
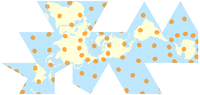
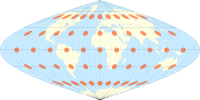
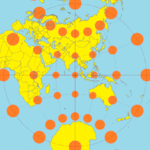
Cartes du monde comparant les indicatrices de Tissot sur certaines projections courantes
Projection équirectangulaire Projection de Mercator Projection Gall-Peters Projection de Mollweide Projection triple de Winkel Projection azimutale équidistante Projection plus complète Projection transversale de Mercator Projection cylindrique de Lambert à aire égale Projection sinusoïdale projection Robinson Projection stéréographique

Mathématiques

Dans l'image adjacente, ABCD est un cercle d'aire unitaire définie dans un modèle sphérique ou ellipsoïdal de la Terre, et A′B′C′D′ est l'indicatrice de Tissot qui résulte de sa projection sur le plan. Le segment OA est transformé en OA', et le segment OB est transformé en OB'. L'échelle linéaire n'est pas conservée selon ces deux directions, puisque OA' n'est pas égal à OA et OB' n'est pas égal à OB. L'angle MOA, dans le cercle d'aire unitaire, est transformé en angle M′OA′ dans l'ellipse de distorsion. Parce que M′OA′ ≠ MOA, nous savons qu'il y a une distorsion angulaire. L'aire du cercle ABCD est, par définition, égale à 1. Comme l'aire de l'ellipse A′B′ est inférieure à 1, une distorsion d'aire s'est produite.

Face à une indicatrice Tissot, différentes notions de rayon entrent en jeu. Le premier est le rayon infinitésimal du cercle d'origine. L'ellipse de distorsion résultante aura également un rayon infinitésimal, mais par les mathématiques des différentiels , les rapports de ces valeurs infinitésimales sont finis. Ainsi, par exemple, si l'ellipse de distorsion résultante est de la même taille infinitésimale que sur la sphère, alors son rayon est considéré comme égal à 1. Enfin, la taille que l'indicateur est dessinée pour une inspection humaine sur la carte est arbitraire. Lorsqu'un tableau d'indicateurs est dessiné sur une carte, ils sont tous mis à l'échelle de la même quantité arbitraire afin que leurs tailles soient proportionnellement correctes.

Comme M dans le schéma, les axes de O le long de la parallèle et le long du méridien peuvent subir un changement de longueur et une rotation lors de la projection. Il est courant dans la littérature de représenter l'échelle le long du méridien par h et l'échelle le long du parallèle par k , pour un point donné. De même, l'angle entre le méridien et le parallèle peut avoir changé de 90° à une autre valeur. En effet, à moins que la carte ne soit conforme, tous les angles sauf celui sous-tendu par le demi-grand axe et le demi-petit axe de l'ellipse peuvent avoir changé. Un angle particulier aura changé le plus, et la valeur de cette variation maximale est appelée la déformation angulaire, noté θ ' . En général, quel angle il s'agit et comment il est orienté ne figurent pas en bonne place dans l'analyse de distorsion. C'est la valeur du changement qui est significative. Les valeurs de h , k et θ ' peuvent être calculés comme suit.

${\displaystyle {\begin{aligned}h&={\frac {1}{R}}{\sqrt {{{\left({\frac {\partial x}{\partial \varphi }}\right)}^ {2}}+{{\left({\frac {\partial y}{\partial \varphi }}\right)}^{2}}}}\\k&={\frac {1}{R\cos \varphi }}{\sqrt {{{\left({\frac {\partial x}{\partial \lambda }}\right)}^{2}}+{{\left({\frac {\partial y }{\partial \lambda }}\right)}^{2}}}}\\\sin \theta '&={\frac {1}{R^{2}hk\cos \varphi }}\left( {{\frac {\partial y}{\partial \varphi }}{\frac {\partial x}{\partial \lambda }}-{\frac {\partial x}{\partial \varphi }}{\frac {\partial y}{\partial \lambda }}}\right)\\a'&={\sqrt {{h^{2}}+{k^{2}}+2hk\sin \theta '}} \\b'&={\sqrt {{h^{2}}+{k^{2}}-2hk\sin \theta '}}\\a&={\frac {a'+b'}{2 }}\\b&={\frac {a'-b'}{2}}\\s&=hk\sin \theta '\\\omega &=2\arcsin \left({\frac {b'}{ a'}}\right)\end{aligned}}}$

où φ et λ sont la latitude et la longitude, x et y sont des coordonnées projetées, et R est le rayon du globe.

Comme résultats, a et b représentent les facteurs d'échelle maximum et minimum au point, ce qui est la même chose que les axes demi-grand et demi-petit de l'ellipse de Tissot ; s représente la quantité d'inflation ou de déflation dans la zone (également donnée par a ∙ b ); et ω représente la distorsion angulaire maximale au point.

Pour la projection de Mercator , et toute autre conformation projection, h  =  k et θ '  = 90 ° de sorte que chaque ellipse dégénère en un cercle avec le rayon h  =  k étant égal au facteur d'échelle dans une direction quelconque à ce point.

Pour la projection sinusoïdale , et toute autre projection à aire égale , le demi-grand axe de l'ellipse est l'inverse du demi-petit axe de sorte que chaque ellipse a la même aire même si leurs excentricités varient.

Pour les projections arbitraires, ni la forme ni la surface des ellipses ne sont liées les unes aux autres en général.

Une dérivation alternative pour le calcul numérique

Une autre façon de comprendre et de dériver l'indicatrice de Tissot est la géométrie différentielle des surfaces. Cette approche se prête bien aux méthodes numériques modernes, car les paramètres de l'indicatrice de Tissot peuvent être calculés en utilisant la décomposition en valeurs singulières (SVD) et l'approximation par différence centrale .

Distance différentielle sur l'ellipsoïde

Soit un point 3D, , sur un ellipsoïde paramétré comme : ${\displaystyle {\hat {X}}}$

${\displaystyle {\hat {X}}(\lambda ,\phi )=\left[{\begin{matrix}N\cos {\lambda }\cos {\phi }\\-N(1-e^{ 2})\sin {\phi }\\N\sin {\lambda }\cos {\phi }\end{matrice}}\right]}$

où sont respectivement la longitude et la latitude, et est fonction du rayon équatorial, , et de l'excentricité, : ${\style d'affichage (\lambda ,\phi )}$${\style d'affichage N}$${\style d'affichage R}$${\style d'affichage e}$

${\displaystyle N={\frac {R}{\sqrt {1-e^{2}\sin ^{2}(\phi )}}}}$

L'élément de distance sur la sphère, est défini par la première forme fondamentale : ${\displaystyle ds}$

${\displaystyle ds^{2}={\begin{bmatrix}d\lambda &d\phi \end{bmatrix}}{\begin{bmatrix}E&F\\F&G\end{bmatrix}}{\begin{bmatrix}d \lambda \\d\phi \end{bmatrix}}}$

dont les coefficients sont définis comme :

${\displaystyle {\begin{aligned}&E={\frac {\partial {\hat {X}}}{\partial \lambda }}{\boldsymbol {\cdot }}{\frac {\partial {\hat { X}}}{\partial \lambda }}\\&F={\frac {\partial {\hat {X}}}{\partial \lambda }}{\boldsymbol {\cdot }}{\frac {\partial {\hat {X}}}{\partial \phi }}\\&G={\frac {\partial {\hat {X}}}{\partial \phi }}{\boldsymbol {\cdot }}{\ frac {\partial {\hat {X}}}{\partial \phi }}\\\end{aligned}}}$

Le calcul des dérivées nécessaires donne :

${\displaystyle {\frac {\partial {\hat {X}}}{\partial \lambda }}=\left[{\begin{matrix}-N\sin {\lambda }\cos {\phi }\\ 0\\N\cos {\lambda }\cos {\phi }\end{matrice}}\right]\qquad \qquad {\frac {\partial {\hat {X}}}{\partial \phi }} =\gauche[{\begin{matrice}-M\cos {\lambda }\sin {\phi }\\-M\cos {\phi }\\M\sin {\lambda }\sin {\phi }\ fin{matrice}}\right]}$

où est fonction du rayon équatorial, , et de l'excentricité de l'ellipsoïde, : ${\style d'affichage M}$${\style d'affichage R}$${\style d'affichage e}$

${\displaystyle M={\frac {R(1-e^{2})}{(1-e^{2}\sin ^{2}(\phi ))^{\frac {3}{2} }}}}$

La substitution de ces valeurs dans la première forme fondamentale donne la formule de la distance élémentaire sur l'ellipsoïde :

${\displaystyle ds^{2}=\left(N\cos {\phi }\right)^{2}d\lambda ^{2}+M^{2}d\phi ^{2}}$

Ce résultat met en relation la mesure de distance sur la surface de l'ellipsoïde en fonction du système de coordonnées sphériques.

Transformer l'élément de distance

Rappelons que le but de l'indicatrice de Tissot est de décrire comment les distances sur la sphère changent lorsqu'elles sont mappées sur une surface plane. Plus précisément, la relation souhaitée est la transformation qui relie la distance différentielle le long des bases du système de coordonnées sphériques à la distance différentielle le long des bases du système de coordonnées cartésiennes sur la carte planaire. Cela peut être exprimé par la relation : ${\displaystyle {\mathcal {T}}}$

${\displaystyle {\begin{bmatrix}dx\\dy\end{bmatrix}}={\mathcal {T}}{\begin{bmatrix}ds(\lambda ,0)\\ds(0,\phi )\ fin{bmatrice}}}$

où et représentent le calcul de le long des axes longitudinal et latitudinal, respectivement. Le calcul de et peut être effectué directement à partir de l'équation ci-dessus, ce qui donne : ${\displaystyle ds(\lambda ,0)}$${\displaystyle ds(0,\phi )}$${\displaystyle ds}$${\displaystyle ds(\lambda ,0)}$${\displaystyle ds(0,\phi )}$

${\displaystyle {\begin{aligned}&ds(\lambda ,0)=N\cos(\phi )d\lambda \\&ds(0,\phi )=Md\phi \end{aligned}}}$

Pour les besoins de ce calcul, il est utile d'exprimer cette relation sous la forme d'une opération matricielle :

${\displaystyle {\begin{bmatrix}d\lambda \\d\phi \end{bmatrix}}=K{\begin{bmatrix}ds(\lambda ,0)\\ds(0,\phi )\end{ bmatrix}},\qquad K={\begin{bmatrix}{\frac {1}{N\cos {\phi }}}&0\\0&{\frac {1}{M}}\end{bmatrix}} }$

Maintenant, afin de relier les distances sur la surface de l'ellipsoïde à celles sur le plan, nous devons relier les systèmes de coordonnées. A partir de la règle de la chaîne, on peut écrire :

${\displaystyle {\begin{bmatrix}dx\\dy\end{bmatrix}}=J{\begin{bmatrix}d\lambda \\d\phi \end{bmatrix}}}$

où J est la matrice Jacobienne :

${\displaystyle J={\begin{bmatrix}{\frac {\partial x}{\partial \lambda }}&{\frac {\partial x}{\partial \phi }}\\{\frac {\partial y}{\partial \lambda }}&{\frac {\partial y}{\partial \phi }}\end{bmatrix}}}$

Le branchement de l'expression matricielle pour et donne la définition de la transformation représentée par l'indicateur : ${\style d'affichage d\lambda }$${\style d'affichage d\phi }$${\displaystyle {\mathcal {T}}}$

${\displaystyle {\begin{bmatrix}dx\\dy\end{bmatrix}}=JK{\begin{bmatrix}ds(\lambda ,0)\\ds(0,\phi )\end{bmatrix}}}$

${\displaystyle {\mathcal {T}}=JK}$

Cette transformation encapsule le mappage de la surface de l'ellipsoïde au plan. Exprimé sous cette forme, le SVD peut être utilisé pour morceler les composantes importantes de la transformation locale. ${\displaystyle {\mathcal {T}}}$

Calcul numérique et SVD

Afin d'extraire les informations de distorsion souhaitées, à n'importe quel endroit donné dans le système de coordonnées sphériques, les valeurs de peuvent être calculées directement. Le Jacobien, , peut être calculé analytiquement à partir de la fonction cartographique elle-même, mais il est souvent plus simple d'approcher numériquement les valeurs à n'importe quel endroit de la carte en utilisant des différences centrales . Une fois ces valeurs calculées, SVD peut être appliqué à chaque matrice de transformation pour extraire les informations de distorsion locales. N'oubliez pas que, comme la distorsion est locale, chaque emplacement sur la carte aura sa propre transformation. ${\style d'affichage K}$${\style d'affichage J}$

Rappelons la définition de SVD :

${\displaystyle \mathrm {SVD} ({\mathcal {T}})=U\Lambda V^{T}}$

C'est la décomposition de la transformation, , en une rotation dans le domaine source (c'est-à-dire la surface de l'ellipsoïde), , une mise à l'échelle le long de la base, , et une seconde rotation subséquente, . Pour comprendre la distorsion, la première rotation n'est pas pertinente, car elle fait tourner les axes du cercle mais n'a aucune incidence sur l'orientation finale de l'ellipse. L'opération suivante, représentée par la matrice diagonale des valeurs singulières, met le cercle à l'échelle le long de ses axes, le déformant en une ellipse. Ainsi, les valeurs singulières représentent les facteurs d'échelle le long des axes de l'ellipse. La première valeur singulière fournit le demi-grand axe, , et la seconde, le demi-petit axe, , qui sont les facteurs de mise à l'échelle directionnels de la distorsion. La distorsion d'échelle peut être calculée comme l'aire de l'ellipse , ou de manière équivalente par le déterminant de . Enfin, l'orientation de l'ellipse, , peut être extraite de la première colonne de as : ${\displaystyle {\mathcal {T}}}$${\displaystyle V^{T}}$${\style d'affichage \Lambda }$${\style d'affichage U}$${\style d'affichage a}$${\style d'affichage b}$${\displaystyle ab}$${\displaystyle {\mathcal {T}}}$${\displaystyle \theta }$${\style d'affichage U}$

${\displaystyle \theta =\arctan \left({\frac {u_{1,0}}{u_{0,0}}}\right)}$

Galerie

Voir également

• Ellipse de MacAdam

Les références

Liens externes

• Applet Java avec projections interactives montrant l'indicatrice de Tissot