Interpolation trilinéaire - Trilinear interpolation

L'interpolation trilinéaire est une méthode d' interpolation multivariée sur une grille régulière à 3 dimensions . Il approche linéairement la valeur d'une fonction à un point intermédiaire dans le prisme rectangulaire axial local , en utilisant des données de fonction sur les points du réseau. Pour un maillage arbitraire et non structuré (comme utilisé dans l' analyse par éléments finis ), d'autres méthodes d'interpolation doivent être utilisées ; si tous les éléments du maillage sont des tétraèdres ( simplices 3D ), alors les coordonnées barycentriques fournissent une procédure simple. ${\style d'affichage (x,y,z)}$

L'interpolation trilinéaire est fréquemment utilisée dans l'analyse numérique , l'analyse de données et l'infographie .

Par rapport à l'interpolation linéaire et bilinéaire

L'interpolation trilinéaire est le prolongement de l'interpolation linéaire , qui opère dans les espaces avec dimension , et de l' interpolation bilinéaire , qui opère avec dimension , à dimension . Ces schémas d'interpolation utilisent tous des polynômes d'ordre 1, donnant une précision d'ordre 2, et nécessitent des valeurs prédéfinies adjacentes entourant le point d'interpolation. Il existe plusieurs façons d'arriver à l'interpolation trilinéaire, qui équivaut à l' interpolation tenseur B-spline tridimensionnelle d'ordre 1, et l'opérateur d'interpolation trilinéaire est également un produit tensoriel de 3 opérateurs d'interpolation linéaire. ${\style d'affichage D=1}$${\style d'affichage D=2}$${\style d'affichage D=3}$${\displaystyle 2^{D}=8}$

Méthode

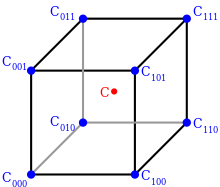
Huit points d'angle sur un cube entourant le point d'interpolation C

Représentation de l'interpolation 3D

Une visualisation géométrique de l'interpolation trilinéaire. Le produit de la valeur au point désiré et du volume total est égal à la somme des produits de la valeur à chaque coin et du volume partiel diagonalement opposé au coin.

Sur un réseau périodique et cubique, soit , , et les différences entre chacun de , , et la plus petite coordonnée liée, c'est-à-dire : ${\displaystyle x_{\text{d}}}$${\displaystyle y_{\text{d}}}$${\displaystyle z_{\text{d}}}$${\style d'affichage x}$${\style d'affichage y}$${\style d'affichage z}$

${\displaystyle {\begin{aligned}x_{\text{d}}={\frac {x-x_{0}}{x_{1}-x_{0}}}\\y_{\text{d} }={\frac {y-y_{0}}{y_{1}-y_{0}}}\\z_{\text{d}}={\frac {z-z_{0}}{z_{ 1}-z_{0}}}\end{aligned}}}$

où indique le point de réseau en dessous et indique le point de réseau au - dessus et de même pour et . ${\style d'affichage x_{0}}$${\style d'affichage x}$${\style d'affichage x_{1}}$${\style d'affichage x}$${\displaystyle y_{0},y_{1},z_{0}}$${\style d'affichage z_{1}}$

Nous interpolons d'abord le long (imaginons que nous "poussions" la face du cube définie par vers la face opposée, définie par ), donnant : ${\style d'affichage x}$${\style d'affichage C_{0jk}}$${\style d'affichage C_{1jk}}$

${\displaystyle {\begin{aligned}c_{00}&=c_{000}(1-x_{\text{d}})+c_{100}x_{\text{d}}\\c_{01} &=c_{001}(1-x_{\text{d}})+c_{101}x_{\text{d}}\\c_{10}&=c_{010}(1-x_{\text {d}})+c_{110}x_{\text{d}}\\c_{11}&=c_{011}(1-x_{\text{d}})+c_{111}x_{\ text{d}}\end{aligned}}}$

Où signifie la valeur de la fonction de Ensuite, nous interpolons ces valeurs (le long de , "poussant" de à ), donnant : ${\style d'affichage c_{000}}$${\style d'affichage (x_{0},y_{0},z_{0}).}$${\style d'affichage y}$${\style d'affichage C_{i0k}}$${\style d'affichage C_{i1k}}$

${\displaystyle {\begin{aligned}c_{0}&=c_{00}(1-y_{\text{d}})+c_{10}y_{\text{d}}\\c_{1} &=c_{01}(1-y_{\text{d}})+c_{11}y_{\text{d}}\end{aligned}}}$

Enfin, nous interpolons ces valeurs le long (en parcourant une ligne): ${\style d'affichage z}$

${\displaystyle c=c_{0}(1-z_{\text{d}})+c_{1}z_{\text{d}}.}$

Cela nous donne une valeur prédite pour le point.

Le résultat de l'interpolation trilinéaire est indépendant de l'ordre des étapes d'interpolation selon les trois axes : tout autre ordre, par exemple selon , puis selon , et enfin selon , produit la même valeur. ${\style d'affichage x}$${\style d'affichage y}$${\style d'affichage z}$

Les opérations ci-dessus peuvent être visualisées comme suit : Nous trouvons d'abord les huit coins d'un cube qui entourent notre point d'intérêt. Ces coins ont les valeurs , , , , , , , . ${\style d'affichage c_{000}}$${\style d'affichage c_{100}}$${\style d'affichage c_{010}}$${\style d'affichage c_{110}}$${\style d'affichage c_{001}}$${\displaystyle c_{101}}$${\style d'affichage c_{011}}$${\style d'affichage c_{111}}$

Ensuite, nous effectuons une interpolation linéaire entre et pour trouver , et pour trouver , et pour trouver , et pour trouver . ${\style d'affichage c_{000}}$${\style d'affichage c_{100}}$${\style d'affichage c_{00}}$${\style d'affichage c_{001}}$${\displaystyle c_{101}}$${\style d'affichage c_{01}}$${\style d'affichage c_{011}}$${\style d'affichage c_{111}}$${\style d'affichage c_{11}}$${\style d'affichage c_{010}}$${\style d'affichage c_{110}}$${\style d'affichage c_{10}}$

Maintenant, nous interpolons entre et pour trouver , et pour trouver . Enfin, nous calculons la valeur par interpolation linéaire de et${\style d'affichage c_{00}}$${\style d'affichage c_{10}}$${\style d'affichage c_{0}}$${\style d'affichage c_{01}}$${\style d'affichage c_{11}}$${\style d'affichage c_{1}}$${\style d'affichage c}$${\style d'affichage c_{0}}$${\style d'affichage c_{1}}$

En pratique, une interpolation trilinéaire est identique à deux interpolations bilinéaires combinées à une interpolation linéaire :

${\displaystyle c\approx l\left(b(c_{000},c_{010},c_{100},c_{110}),\,b(c_{001},c_{011},c_{101 },c_{111})\droit)}$

Algorithme alternatif

Une autre façon d'écrire la solution au problème d'interpolation est

${\displaystyle f(x,y,z)\approx a_{0}+a_{1}x+a_{2}y+a_{3}z+a_{4}xy+a_{5}xz+a_{ 6}yz+a_{7}xyz}$

où les coefficients sont trouvés en résolvant le système linéaire

${\displaystyle {\begin{aligned}{\begin{bmatrix}1&x_{0}&y_{0}&z_{0}&x_{0}y_{0}&x_{0}z_{0}&y_{0}z_{0 }&x_{0}y_{0}z_{0}\\1&x_{1}&y_{0}&z_{0}&x_{1}y_{0}&x_{1}z_{0}&y_{0}z_{0 }&x_{1}y_{0}z_{0}\\1&x_{0}&y_{1}&z_{0}&x_{0}y_{1}&x_{0}z_{0}&y_{1}z_{0 }&x_{0}y_{1}z_{0}\\1&x_{1}&y_{1}&z_{0}&x_{1}y_{1}&x_{1}z_{0}&y_{1}z_{0 }&x_{1}y_{1}z_{0}\\1&x_{0}&y_{0}&z_{1}&x_{0}y_{0}&x_{0}z_{1}&y_{0}z_{1 }&x_{0}y_{0}z_{1}\\1&x_{1}&y_{0}&z_{1}&x_{1}y_{0}&x_{1}z_{1}&y_{0}z_{1 }&x_{1}y_{0}z_{1}\\1&x_{0}&y_{1}&z_{1}&x_{0}y_{1}&x_{0}z_{1}&y_{1}z_{1 }&x_{0}y_{1}z_{1}\\1&x_{1}&y_{1}&z_{1}&x_{1}y_{1}&x_{1}z_{1}&y_{1}z_{1 }&x_{1}y_{1}z_{1}\end{bmatrix}}{\begin{bmatrix}a_{0}\\a_{1}\\a_{2}\\a_{3}\\a_ {4}\\a_{5}\\a_{6}\\a_{7}\end{bmatrix}}={\begin{bmatrix}c_{000}\\c_{100}\\c_{010} \\c_{110}\\c_{001}\\c_{101}\\c_{011}\\c_{111}\end{bmatrix}},\end{aligned}}}$

donner le résultat

${\displaystyle {\begin{aligned}a_{0}={}&{\frac {-c_{000}x_{1}y_{1}z_{1}+c_{001}x_{1}y_{1 }z_{0}+c_{010}x_{1}y_{0}z_{1}-c_{011}x_{1}y_{0}z_{0}}{(x_{0}-x_{1 })(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {c_{100}x_{0}y_{1}z_{ 1}-c_{101}x_{0}y_{1}z_{0}-c_{110}x_{0}y_{0}z_{1}+c_{111}x_{0}y_{0}z_ {0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{1} ={}&{\frac {c_{000}y_{1}z_{1}-c_{001}y_{1}z_{0}-c_{010}y_{0}z_{1}+c_{011 }y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\ \&{\frac {-c_{100}y_{1}z_{1}+c_{101}y_{1}z_{0}+c_{110}y_{0}z_{1}-c_{111} y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt ]a_{2}={}&{\frac {c_{000}x_{1}z_{1}-c_{001}x_{1}z_{0}-c_{010}x_{1}z_{1 }+c_{011}x_{1}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})} }+{}\\&{\frac {-c_{100}x_{0}z_{1}+c_{101}x_{0}z_{0}+c_{110}x_{0}z_{1} -c_{111}x_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}} ,\\[4pt]a_{3}={}&{\frac {c_{000}x_{1}y_{1}-c_{001}x_{1}y_{1}-c_{010}x_{ 1}y_{0}+c_{011}x_{1}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_ {1})}}+{}\\&{\frac {-c_{100}x_{0}y_{1}+c_{101}x_{0}y_{1}+c_{110}x_{0 }y_{0}-c_{111}x_{0}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{ 1})}},\\[4pt]a_{4}={}&{\frac {-c_{000}z_{1}+c_{001}z_{0}+c_{010}z_{1} -c_{011}z_{0}+c_{100}z_{1}-c_{101}z_{0}-c_{110}z_{1}+c_{111}z_{0}}{(x_{ 0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{5}=&{\frac {-c_ {000}a_{1}+c_{001}a_{1}+c_{010}a_{0}-c_{011}a_{0}+c_{100}a_{1}-c_{101}a_{ 1}-c_{110}y_{0}+c_{111}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}- z_{1})}},\\[4pt]a_{6}={}&{\frac {-c_{000}x_{1}+c_{001}x_{1}+c_{010}x_{ 1}-c_{011}x_{1}+c_{100}x_{0}-c_{101}x_{0}-c_{110}x_{0}+c_{111}x_{0}}{( x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{7}={}&{\ frac {c_{000}-c_{001}-c_{010}+c_{011}-c_{100}+c_{101}+c_{110}-c_{111}}{(x_{0}-x_ {1})(y_{0}-y_{1})(z_{0}-z_{1})}}.\end{aligned}}}$

Voir également

• Interpolation linéaire
• Interpolation bilinéaire
• Interpolation tricubique
• Interpolation radiale
• Interpolation tétraédrique

Liens externes

• pseudo-code de la NASA , décrit une interpolation trilinéaire inverse itérative (étant donné les sommets et la valeur de C trouver Xd, Yd et Zd).
• Paul Bourke, Méthodes d'interpolation , 1999. Contient une méthode très intelligente et simple pour trouver une interpolation trilinéaire basée sur la logique binaire et pouvant être étendue à n'importe quelle dimension (tétralinéaire, pentalinéaire, ...).
• Kenwright, déformation du tétraèdre de forme libre. Symposium international sur l'informatique visuelle. Éditions internationales Springer, 2015 [1] .