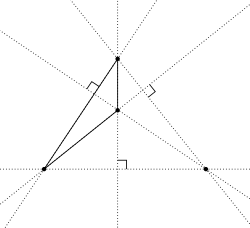
Système orthocentrique - Orthocentric system

Système orthocentrique . Tout point est l'orthocentre du triangle formé par les trois autres.

En géométrie , un système orthocentrique est un ensemble de quatre points sur un plan , dont l'un est l' orthocentre du triangle formé par les trois autres.

Si quatre points forment un système orthocentrique, alors chacun des quatre points est l'orthocentre des trois autres. Ces quatre triangles possibles auront tous le même cercle de neuf points . Par conséquent , ces quatre triangles possibles doivent tous avoir circonscrits avec le même cercle circonscrit .

Le cercle commun à neuf points

Cercle commun à neuf points , où O, O ₄ et A ₄ sont respectivement le centre, le circoncentrique et l'orthocentre à neuf points du triangle formé à partir des trois autres points orthocentriques A ₁ , A ₂ et A ₃ .

Le centre de ce cercle commun à neuf points se situe au centre de gravité des quatre points orthocentriques. Le rayon du cercle commun à neuf points est la distance entre le centre de neuf points et le point médian de l'un des six connecteurs qui rejoignent toute paire de points orthocentriques par lesquels passe le cercle commun à neuf points. Le cercle à neuf points passe également par les trois intersections orthogonales aux pieds des altitudes des quatre triangles possibles.

Ce centre commun à neuf points se situe au milieu du connecteur qui relie tout point orthocentrique au circoncentrique du triangle formé à partir des trois autres points orthocentriques.

Le cercle commun à neuf points est tangent aux 16 cercles et excercles des quatre triangles dont les sommets forment le système orthocentrique.

Le triangle orthique commun, son stimulateur et ses excentres

Si les six connecteurs qui joignent une paire de points orthocentriques sont étendus à six lignes qui se croisent, ils génèrent sept points d'intersection. Quatre de ces points sont les points orthocentriques d'origine et les trois points supplémentaires sont les intersections orthogonales aux pieds des altitudes . La jonction de ces trois points orthogonaux en un triangle génère un triangle orthique qui est commun aux quatre triangles possibles formés à partir des quatre points orthocentriques pris trois à la fois.

L' incenteur de ce triangle orthique commun doit être l'un des quatre points orthocentriques d'origine. De plus, les trois points restants deviennent les excentres de ce triangle orthique commun. Le point orthocentrique qui devient le stimulant du triangle orthique est le point orthocentrique le plus proche du centre commun à neuf points. Cette relation entre le triangle orthique et les quatre points orthocentriques d'origine conduit directement au fait que l'incenteur et les excentres d'un triangle de référence forment un système orthocentrique.

Il est normal de distinguer l'un des points orthocentriques des autres, en particulier celui qui est le stimulant du triangle orthique; celui-ci est noté H comme orthocentre des trois points orthocentriques externes choisis comme triangle de référence ABC . Dans cette configuration normalisée, le point H se trouvera toujours dans le triangle ABC , et tous les angles du triangle ABC seront aigus. Les quatre triangles possibles mentionnés ci-dessus sont alors les triangles ABC , ABH , ACH et BCH . Les six connecteurs mentionnés ci-dessus sont AB , AC , BC , AH , BH et CH . Les sept intersections mentionnées ci-dessus sont A , B , C , H (les points orthocentriques d'origine) et H _A , H _B , H _C (les pieds des altitudes du triangle ABC et les sommets du triangle orthique).

Le système orthocentrique et ses axes orthiques

L'axe orthique associé à un système orthocentrique normalisé A , B , C et H , où ABC est le triangle de référence, est une ligne qui passe par trois points d'intersection formés lorsque chaque côté du triangle orthique rencontre chaque côté du triangle de référence. Considérons maintenant les trois autres triangles possibles, ABH , ACH et BCH . Ils ont chacun leur propre axe orthique.

Lignes d'Euler et systèmes orthocentriques homothétiques

Système orthocentrique . Où O ₁ , O ₂ , O ₃ et O ₄ sont les circoncentres des quatre triangles possibles formés à partir des points orthocentriques A ₁ , A ₂ , A ₃ et A ₄ .

Soit les vecteurs a , b , c et h la position de chacun des quatre points orthocentriques et soit n = ( a + b + c + h ) / 4 le vecteur de position de N, le centre commun à neuf points. Joignez chacun des quatre points orthocentriques à leur centre commun à neuf points et prolongez-les en quatre lignes. Ces quatre lignes représentent maintenant les lignes d'Euler des quatre triangles possibles où la ligne étendue HN est la ligne d'Euler du triangle ABC et la ligne étendue AN est la ligne d'Euler du triangle BCH etc. Si un point P est choisi sur la ligne d'Euler HN du triangle de référence ABC avec un vecteur de position p tel que p = n + α ( h  -  n ) où α est une constante pure indépendante du positionnement des quatre points orthocentriques et de trois autres points P _A , P _B , P _C tels que p _a = n + α ( a  -  n ) etc., alors P , P _A , P _B , P _C forment un système orthocentrique. Ce système orthocentrique généré est toujours homothétique au système original de quatre points avec le centre commun à neuf points comme centre homothétique et α le rapport de similitude .

Lorsque P est choisi comme centre de gravité G , alors α = −1/3. Lorsque P est choisi comme circoncentrique O, alors α = -1 et le système orthocentrique généré est congruent au système d'origine et en est le reflet autour du centre à neuf points. Dans cette configuration P _A , P _B , P _C forment un triangle de Johnson du triangle de référence original ABC . Par conséquent , les cercles circonscrits des quatre triangles ABC , ABH , ACH , BCH sont tous égaux et forment un ensemble de Johnson cercles comme représenté sur le schéma adjacent.

Autres propriétés

Les quatre lignes d'Euler d'un système orthocentrique sont orthogonales aux quatre axes orthiques d'un système orthocentrique.

Les six connecteurs qui joignent n'importe quelle paire des quatre points orthocentriques d'origine produiront des paires de connecteurs orthogonaux l'un par rapport à l'autre de sorte qu'ils satisfassent les équations de distance.

${\ displaystyle AB ^ {2} + CH ^ {2} = AC ^ {2} + BH ^ {2} = BC ^ {2} + AH ^ {2} = 4R ^ {2}}$

où R est le circumradius commun des quatre triangles possibles. Ces équations ainsi que la loi des sinus aboutissent à l'identité

${\ displaystyle {\ frac {BC} {\ sin {A}}} = {\ frac {AC} {\ sin {B}}} = {\ frac {AB} {\ sin {C}}} = {\ frac {HA} {| \ cos {A} |}} = {\ frac {HB} {| \ cos {B} |}} = {\ frac {HC} {| \ cos {C} |}} = 2R .}$

Le théorème de Feuerbach stipule que le cercle de neuf points est tangent au cercle incorporé et aux trois excercles d'un triangle de référence. Parce que le cercle à neuf points est commun aux quatre triangles possibles dans un système orthocentrique, il est tangent à 16 cercles comprenant les cercles et les excercles des quatre triangles possibles.

Toute conique passant par les quatre points orthocentriques ne peut être qu'une hyperbole rectangulaire . Ceci est le résultat du théorème conique de Feuerbach qui stipule que pour toutes les circonconiques d'un triangle de référence qui passe également par son orthocentre, le lieu du centre de ces circonconiques forme le cercle à neuf points et que les circonconiques ne peuvent être que des hyperboles rectangulaires. Le lieu des perspectives de cette famille d'hyperboles rectangulaires se situera toujours sur les quatre axes orthiques. Donc, si une hyperbole rectangulaire est dessinée à travers quatre points orthocentriques, elle aura un centre fixe sur le cercle commun à neuf points mais elle aura quatre perspectives une sur chacun des axes orthiques des quatre triangles possibles. Le point unique sur le cercle de neuf points qui est le centre de cette hyperbole rectangulaire aura quatre définitions différentes en fonction de laquelle des quatre triangles possibles est utilisé comme triangle de référence.

Les hyperboles rectangulaires bien documentées qui passent par quatre points orthocentriques sont les circumhyperboles de Feuerbach, Jeřábek et Kiepert du triangle de référence ABC dans un système normalisé avec H comme orthocentre.

Les quatre triangles possibles ont un ensemble de quatre inconvénients connus sous le nom d'inconics orthiques qui partagent certaines propriétés. Les contacts de ces inconics avec les quatre triangles possibles se produisent aux sommets de leur triangle orthique commun. Dans un système orthocentrique normalisé, l'inconique orthique tangente aux côtés du triangle ABC est une inellipse et les inconvénients orthiques des trois autres triangles possibles sont des hyperboles. Ces quatre inconics orthiques partagent également le même point de Brianchon , H, le point orthocentrique le plus proche du centre commun à neuf points. Les centres de ces inconics orthiques sont les points symédiens , K des quatre triangles possibles.

Il existe de nombreuses cubiques documentées qui traversent un triangle de référence et son orthocentre. Le circcubique dit orthocubique - K006 est intéressant en ce qu'il passe par trois systèmes orthocentriques ainsi que les trois sommets du triangle orthique (mais pas l'orthocentre du triangle orthique). Les trois systèmes orthocentriques sont l'incenteur et les excentres, le triangle de référence et son orthocentre et enfin l'orthocentre du triangle de référence avec les trois autres points d'intersection que cette cubique a avec le cercle circulaire du triangle de référence.

Deux cercles polaires de deux triangles dans un système orthocentrique sont orthogonaux .

Les références

Liens externes

• Weisstein, Eric W. "Orthocentre" . MathWorld .
• Weisstein, Eric W. "Théorème de Feuerbach" . MathWorld .
• Weisstein, Eric W. "Théorème conique de Feuerbach" . MathWorld .
• Weisstein, Eric W. "Hyperbole Feuerbach" . MathWorld .
• Weisstein, Eric W. «Hyperbole de Jerabek» . MathWorld .
• Weisstein, Eric W. «Hyperbole de Kiepert» . MathWorld .
• Weisstein, Eric W. "Orthic Inconic" . MathWorld .
• Weisstein, Eric W. "Axe orthique" . MathWorld .
• Weisstein, Eric W. "Perspecteur" . MathWorld .
• Bernard Gibert Circumcubic K006
• Clark Kimberling, " Encyclopédie des centres triangulaires ". (Répertorie quelque 5000 points intéressants associés à n'importe quel triangle.)