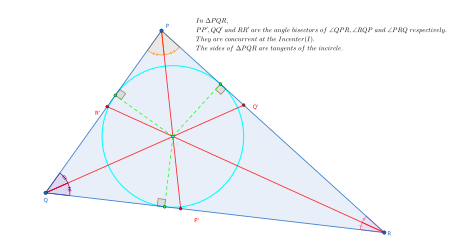
Au centre - Incenter

Le point d'intersection des bissectrices des 3 angles du triangle ABC est le centre (noté I). Le cercle inscrit (dont le centre est I) touche chaque côté du triangle.

En géométrie , le centre d'un triangle est un centre de triangle , un point défini pour tout triangle d'une manière indépendante du placement ou de l'échelle du triangle. L'incenter peut être défini de manière équivalente comme le point où les bissectrices internes du triangle se croisent, comme le point équidistant des côtés du triangle, comme le point de jonction de l' axe médian et le point le plus interne de la transformation grassfire du triangle, et comme le centre du cercle inscrit du triangle.

En collaboration avec le centre de gravité , circumcenter et orthocenter , il est l' un des quatre centres de triangle connus des anciens Grecs, et le seul qui ne relève pas en général sur la ligne d' Euler . Il est le premier centre énuméré, X (1), dans Clark Kimberling l » Encyclopédie des centres Triangle , et l' élément d'identité du groupe multiplicatif des centres de triangle.

Pour les polygones avec plus de trois côtés, le centre n'existe que pour les polygones tangentiels - ceux qui ont un cercle inscrit tangent à chaque côté du polygone. Dans ce cas, l'incenter est le centre de ce cercle et est également éloigné de tous les côtés.

Définition et construction

C'est un théorème de la géométrie euclidienne que les trois bissectrices intérieures d'un triangle se rencontrent en un seul point. Dans Euclide de Eléments , Proposition 4 du livre IV prouve que ce point est aussi le centre du cercle inscrit du triangle. Le cercle inscrit lui-même peut être construit en laissant tomber une perpendiculaire du centre à l'un des côtés du triangle et en dessinant un cercle avec ce segment comme rayon.

L'incenter se trouve à égale distance des trois segments de ligne formant les côtés du triangle, ainsi que des trois lignes contenant ces segments. C'est le seul point également éloigné des segments de ligne, mais il y a trois autres points également éloignés des lignes, les excentres, qui forment les centres des excercles du triangle donné. L'incenter et l'excenter forment ensemble un système orthocentrique .

L' axe médian d'un polygone est l'ensemble des points dont le plus proche voisin sur le polygone n'est pas unique : ces points sont équidistants de deux ou plusieurs côtés du polygone. Une méthode de calcul des axes médians utilise la transformée grassfire , dans laquelle on forme une séquence continue de courbes décalées , chacune à une certaine distance fixe du polygone ; l'axe médian est tracé par les sommets de ces courbes. Dans le cas d'un triangle, l'axe médian se compose de trois segments des bissectrices d'angle, reliant les sommets du triangle au centre, qui est le point unique sur la courbe de décalage la plus interne. Le squelette droit , défini de manière similaire à partir d'un type différent de courbe décalée, coïncide avec l'axe médian pour les polygones convexes et a donc également sa jonction au centre.

Preuves

Preuve de ratio

Soit la bissection de et se rencontrent à , et la bissection de et se rencontrent à , et et se rencontrent à . ${\displaystyle \angle {BAC}}$${\displaystyle {\overline {BC}}}$${\style d'affichage D}$${\displaystyle \angle {ABC}}$${\displaystyle {\overline {AC}}}$${\style d'affichage E}$${\displaystyle {\overline {AD}}}$${\displaystyle {\overline {BE}}}$${\style d'affichage {I}}$

Et laissez -vous rencontrer à . ${\displaystyle {\overline {CI}}}$${\displaystyle {\overline {AB}}}$${\style d'affichage {F}}$

Ensuite, nous devons prouver que c'est la bissection de . ${\displaystyle {\overline {CI}}}$${\displaystyle \angle {ACB}}$

Dans , . ${\displaystyle \triangle {ACF}}$${\displaystyle {\overline {AC}} :{\overline {AF}}={\overline {CI}} :{\overline {IF}}}$

Dans , . ${\displaystyle \triangle {BCF}}$${\displaystyle {\overline {BC}} :{\overline {BF}}={\overline {CI}} :{\overline {IF}}}$

Par conséquent, , de sorte que . ${\displaystyle {\overline {AC}} :{\overline {AF}}={\overline {BC}} :{\overline {BF}}}$${\displaystyle {\overline {AC}} :{\overline {BC}}={\overline {AF}} :{\overline {BF}}}$

Ainsi est la bissection de${\displaystyle {\overline {CF}}}$${\displaystyle \angle {ACB}}$

Preuve perpendiculaire

Une ligne qui est une bissectrice est équidistante de ses deux lignes lors de la mesure par la perpendiculaire. Au point d'intersection de deux bissectrices, ce point est perpendiculairement équidistant des lignes de formation de l'angle final (car elles sont à la même distance de ce bord opposé de l'angle), et se trouve donc sur sa ligne bissectrice d'angle.

Relation avec les côtés et les sommets du triangle

Coordonnées trilinéaires

Les coordonnées trilinéaires d'un point du triangle donnent le rapport des distances aux côtés du triangle. Les coordonnées trilinéaires du centre sont données par

${\style d'affichage \ 1:1:1.}$

La collection de centres de triangles peut recevoir la structure d'un groupe sous la multiplication coordonnée de coordonnées trilinéaires ; dans ce groupe, l'incenter forme l' élément d'identité .

Coordonnées barycentriques

Les coordonnées barycentriques d'un point dans un triangle donnent des poids tels que le point est la moyenne pondérée des positions des sommets du triangle. Les coordonnées barycentriques du centre sont données par

${\style d'affichage \ a:b:c}$

où , , et sont les longueurs des côtés du triangle, ou de manière équivalente (en utilisant la loi des sinus ) par ${\style d'affichage a}$${\style d'affichage b}$${\style d'affichage c}$

${\displaystyle \sin(A):\sin(B):\sin(C)}$

où , , et sont les angles aux trois sommets. ${\style d'affichage A}$${\style d'affichage B}$${\style d'affichage C}$

Coordonnées cartésiennes

Les coordonnées cartésiennes de l'incenter sont une moyenne pondérée des coordonnées des trois sommets en utilisant les longueurs des côtés du triangle par rapport au périmètre - c'est-à-dire en utilisant les coordonnées barycentriques données ci-dessus, normalisées pour sommer à l'unité - comme poids. (Les poids sont positifs de sorte que le centre se trouve à l'intérieur du triangle comme indiqué ci-dessus.) Si les trois sommets sont situés à , , et , et que les côtés opposés à ces sommets ont des longueurs correspondantes , , et , alors le centre est à ${\style d'affichage (x_{A},y_{A})}$${\style d'affichage (x_{B},y_{B})}$${\style d'affichage (x_{C},y_{C})}$${\style d'affichage a}$${\style d'affichage b}$${\style d'affichage c}$

${\displaystyle {\bigg (}{\frac {ax_{A}+bx_{B}+cx_{C}}{a+b+c}},{\frac {ay_{A}+by_{B}+ cy_{C}}{a+b+c}}{\bigg )}={\frac {a(x_{A},y_{A})+b(x_{B},y_{B})+c (x_{C},y_{C})}{a+b+c}}.}$

Distances aux sommets

En désignant le centre du triangle ABC comme I , les distances du centre aux sommets combinées avec les longueurs des côtés du triangle obéissent à l'équation

${\displaystyle {\frac {IA\cdot IA}{CA\cdot AB}}+{\frac {IB\cdot IB}{AB\cdot BC}}+{\frac {IC\cdot IC}{BC\cdot CA}}=1.}$

En outre,

${\displaystyle IA\cdot IB\cdot IC=4Rr^{2},}$

où R et r sont respectivement le circumradius et le inradius du triangle .

Constructions associées

Autres centres

La distance entre le centre et le centre de gravité est inférieure à un tiers de la longueur de la plus longue médiane du triangle.

Par le théorème d'Euler en géométrie , la distance au carré du centre I au centre circonscrit O est donnée par

${\displaystyle OI^{2}=R(R-2r),}$

où R et r sont respectivement le circumradius et le inradius ; ainsi le circumradius est au moins deux fois le inradius, avec égalité seulement dans le cas équilatéral .

La distance du centre au centre N du cercle à neuf points est

${\displaystyle IN={\frac {1}{2}}(R-2r)<{\frac {1}{2}}R.}$

La distance au carré de l'incenter à l' orthocentre H est

${\displaystyle IH^{2}=2r^{2}-4R^{2}\cos A\cos B\cos C.}$

Les inégalités comprennent :

${\displaystyle IG<HG,\quad IH<HG,\quad IG<IO,\quad 2IN<IO.}$

L'incenter est le point de Nagel du triangle médian (le triangle dont les sommets sont les milieux des côtés) et se trouve donc à l'intérieur de ce triangle. Inversement, le point de Nagel de tout triangle est le centre de son triangle anticomplémentaire .

L'incentre doit se situer à l'intérieur d'un disque dont le diamètre relie le centre de gravité G et l' orthocentre H (le disque orthocentroïde ), mais il ne peut pas coïncider avec le centre à neuf points , dont la position est fixée à 1/4 de la longueur du diamètre (plus proche de G ). Tout autre point dans le disque orthocentroïde est le centre d'un triangle unique.

ligne d'Euler

La ligne d'Euler d'un triangle est une ligne passant par son centre circonscrit , son centre de gravité et son orthocentre , entre autres points. L'incenter ne se trouve généralement pas sur la ligne d'Euler ; il n'est sur la droite d'Euler que pour les triangles isocèles , pour lesquels la droite d'Euler coïncide avec l'axe de symétrie du triangle et contient tous les centres des triangles.

Désignant la distance de l'incenter à la ligne d'Euler comme d , la longueur de la médiane la plus longue comme v , la longueur du côté le plus long comme u , le cercle circonscrit comme R , la longueur du segment de droite d'Euler de l'orthocentre au centre circonscrit comme e , et le demi-périmètre comme s , les inégalités suivantes sont vérifiées :

${\displaystyle {\frac {d}{s}}<{\frac {d}{u}}<{\frac {d}{v}}<{\frac {1}{3}};}$

${\displaystyle d<{\frac {1}{3}}e;}$

${\displaystyle d<{\frac {1}{2}}R.}$

Séparateurs de zone et de périmètre

Toute ligne passant par un triangle qui divise à la fois l'aire du triangle et son périmètre en deux passe par le centre du triangle ; chaque ligne passant par le centre qui divise la zone en deux divise également le périmètre en deux. Il y a une, deux ou trois de ces lignes pour un triangle donné.

Distances relatives à une bissectrice

Soit X un point variable sur la bissectrice interne de A . Alors X = I (le centre) maximise ou minimise le rapport le long de cette bissectrice. ${\style d'affichage {\tfrac {BX}{CX}}}$

Les références

Liens externes

• Weisstein, Eric W. "Incenter" . MathWorld .