Densité (polytope) - Density (polytope)

En géométrie , la densité d'un polyèdre en étoile est une généralisation du concept de nombre d'enroulements de deux dimensions à des dimensions supérieures, représentant le nombre d' enroulements du polyèdre autour du centre de symétrie du polyèdre. Il peut être déterminé en faisant passer un rayon du centre à l'infini, en passant uniquement par les facettes du polytope et non par des caractéristiques dimensionnelles inférieures, et en comptant le nombre de facettes qu'il traverse. Pour les polyèdres pour lesquels ce comptage ne dépend pas du choix du rayon, et pour lesquels le point central n'est lui-même sur aucune facette, la densité est donnée par ce comptage de facettes croisées.
Le même calcul peut être effectué pour n'importe quel polyèdre convexe , même sans symétrie, en choisissant n'importe quel point à l'intérieur du polyèdre comme centre. Pour ces polyèdres, la densité sera de 1. Plus généralement, pour tout polyèdre non auto-intersectif (acoptique), la densité peut être calculée comme 1 par un calcul similaire qui choisit un rayon à partir d'un point intérieur qui ne passe que par des facettes de le polyèdre, en ajoute un lorsque ce rayon passe de l'intérieur vers l'extérieur du polyèdre, et en soustrait un lorsque ce rayon passe de l'extérieur à l'intérieur du polyèdre. Cependant, cette affectation des signes aux croisements ne s'applique généralement pas aux polyèdres en étoile, car ils n'ont pas un intérieur et un extérieur bien définis.
Les pavages avec des faces superposées peuvent définir de la même manière la densité comme le nombre de revêtements de faces sur un point donné.
Polygones
La densité d'un polygone est le nombre de fois que la limite polygonale s'enroule autour de son centre. Pour les polygones convexes, et plus généralement les polygones simples (non auto-coupants), la densité est de 1, d'après le théorème de la courbe de Jordan .
La densité d'un polygone peut également être appelée son numéro de virage ; la somme des angles de virage de tous les sommets divisée par 360 °. Ce sera un entier pour tous les chemins unicursaux dans un plan.
La densité d'un polygone composé est la somme des densités des polygones composants.
Polygones d'étoiles régulières
Pour un polygone en étoile régulier { p / q }, la densité est q . Il peut être déterminé visuellement en comptant le nombre minimum de croisements d'arêtes d'un rayon du centre à l'infini.
Exemples
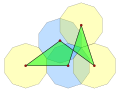
Un polygone à croisement unique, comme ce pentagone équilatéral , a une densité de 0.
Le pentagone régulier {5} a une densité de 1.
Le tétradécagon isotoxique , {(7/2) α }, a une densité 2, similaire à {7/2} régulière.
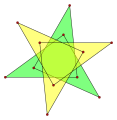
L'heptagramme {7/3} a une densité de 3.
L' hexagramme isotoxique (composé) 2 {(3/2) α } a une densité de 4.
Le dodécagramme isotoxique , {(6/5) α }, a une densité de 5, similaire à la normale {12/5}.
Polyèdres
Un polyèdre et son double ont la même densité.
Courbure totale
Un polyèdre peut être considéré comme une surface avec une courbure gaussienne concentrée aux sommets et définie par un défaut angulaire . La densité d'un polyèdre est égale à la courbure totale (additionnée sur tous ses sommets) divisée par 4π.
Par exemple, un cube a 8 sommets, chacun avec 3 carrés , laissant un défaut d'angle de π / 2. 8 × π / 2 = 4π. La densité du cube est donc de 1.
Polyèdres simples
La densité d'un polyèdre avec des faces simples et des figures de sommets est la moitié de la caractéristique d'Euler , χ. Si son genre est g , sa densité est de 1 à g .
- χ = V - E + F = 2 D = 2 (1- g ).
La densité du polyèdre de sphère topologique est un , comme un cube .
v = 8, e = 12, f = 6.La densité d'un polyèdre toroïdal de genre 1 est nulle , comme cette forme hexagonale: v = 24, e = 48, f = 24.
La densité d'un toroïdal de genre 5 est -4 , comme ce Stewart_toroid :
v = 72, e = 168, f = 88.
Polyèdres étoilés réguliers
Arthur Cayley a utilisé la densité comme un moyen de modifier la formule du polyèdre d'Euler ( V - E + F = 2) pour travailler pour les polyèdres en étoile régulière , où d v est la densité d'une figure de sommet , d f d'une face et D du polyèdre dans son ensemble:
Par exemple, le grand icosaèdre , {3, 5/2}, a 20 faces triangulaires ( d f = 1), 30 arêtes et 12 sommets pentagrammiques ( d v = 2), ce qui donne
- 2 · 12-30 + 1 · 20 = 14 = 2 D .
Cela implique une densité de 7. La formule du polyèdre d'Euler non modifiée échoue pour le petit dodécaèdre étoilé {5/2, 5} et son double grand dodécaèdre {5, 5/2}, pour lequel V - E + F = −6.
Les polyèdres stellaires réguliers existent en deux paires doubles, chaque figure ayant la même densité que son double: une paire (petit dodécaèdre étoilé - grand dodécaèdre) a une densité de 3, tandis que l'autre ( grand dodécaèdre étoilé - grand icosaèdre) a un densité de 7.

|

|
| Le grand icosaèdre non convexe , {3,5 / 2} a une densité de 7 comme le montre cette vue transparente et en coupe à droite. | |
Polyèdres étoile générale
Edmund Hess a généralisé la formule des polyèdres en étoile avec différents types de visage, dont certains peuvent se replier vers l'arrière par rapport à d'autres. La valeur résultante de la densité correspond au nombre de fois où le polyèdre sphérique associé couvre la sphère.
Cela a permis à Coxeter et al. pour déterminer les densités de la majorité des polyèdres uniformes , qui ont un type de sommet et plusieurs types de faces.
La densité d'un prisme octogonal , enroulé deux fois est de 2 , {8/2} × {}, représentée ici avec des sommets décalés pour plus de clarté.
v = 16, e = 24
f 1 = 8 {4}, f 2 = 2 {8/2}
avec d f1 = 1, d f2 = 2, d v = 1.La densité d'un prisme pentagrammique , {5/2} × {} est de 2 .
v = 10, e = 15,
f 1 = 5 {4}, f 2 = 2 {5/2},
d f1 = 1, d f2 = 2.
Polyèdres non orientables
Pour les hémipolyèdres , dont certaines faces passent par le centre, la densité ne peut pas être définie. Les polyèdres non orientables n'ont pas non plus des densités bien définies.
4-polytopes réguliers

Il existe 10 4-polytopes en étoile régulière (appelés les 4-polytopes Schläfli – Hess ), qui ont des densités comprises entre 4, 6, 20, 66, 76 et 191. Ils se présentent par paires doubles, à l'exception de l'auto-double Densité-6 et densité-66 chiffres.
Remarques
Les références
- Coxeter, HSM; Regular Polytopes , (3e édition, 1973), édition Dover, ISBN 0-486-61480-8
- Coxeter, HSM ; Longuet-Higgins, MS; Miller, JCP (1954), "Uniform polyèdres", Philosophical Transactions of the Royal Society of London. Série A. Sciences mathématiques et physiques , 246 (916): 401–450, doi : 10.1098 / rsta.1954.0003 , ISSN 0080-4614 , JSTOR 91532 , MR 0062446
- Wenninger, Magnus J. (1979), "Une introduction à la notion de densité polyédrique", Modèles sphériques , Archives CUP, pp. 132–134 , ISBN 978-0-521-22279-2