Problème de secrétaire - Secretary problem

Graphiques des probabilités d'obtenir le meilleur candidat (cercles rouges) à partir de n applications, et k / n (croix bleues) où k est la taille de l'échantillon

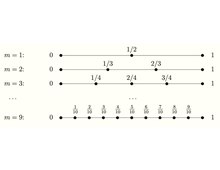
Le problème du secrétaire démontre un scénario impliquant la théorie de l' arrêt optimal qui est largement étudiée dans les domaines des probabilités appliquées , des statistiques et de la théorie de la décision . Il est également connu comme le problème du mariage , le problème de la dot du sultan, le problème du prétendant pointilleux , le jeu googol et le problème du meilleur choix .

La forme de base du problème est la suivante : imaginez un administrateur qui souhaite embaucher la meilleure secrétaire parmi les candidats pouvant être classés pour un poste. Les candidats sont interrogés un par un dans un ordre aléatoire. Une décision concernant chaque candidat en particulier doit être prise immédiatement après l'entretien. Une fois rejeté, un candidat ne peut pas être rappelé. Au cours de l'entretien, l'administrateur obtient des informations suffisantes pour classer le candidat parmi tous les candidats interrogés jusqu'à présent, mais n'est pas au courant de la qualité des candidats encore invisibles. La question porte sur la stratégie optimale ( règle d'arrêt ) pour maximiser la probabilité de sélectionner le meilleur candidat. Si la décision peut être reportée à la fin, cela peut être résolu par le simple algorithme de sélection du maximum consistant à suivre le maximum courant (et qui l'a atteint) et à sélectionner le maximum global à la fin. La difficulté est que la décision doit être prise immédiatement. ${\style d'affichage n}$

La preuve rigoureuse la plus courte connue à ce jour est fournie par l' algorithme des cotes . Cela implique que la probabilité de gain optimale est toujours au moins (où e est la base du logarithme népérien ), et que cette dernière tient même dans une généralité beaucoup plus grande. La règle d'arrêt optimale prescrit de toujours rejeter les premiers candidats interrogés, puis de s'arrêter au premier candidat qui est meilleur que tous les candidats interrogés jusqu'à présent (ou de continuer jusqu'au dernier candidat si cela ne se produit jamais). Parfois, cette stratégie est appelée règle d'arrêt, car la probabilité de s'arrêter au meilleur candidat avec cette stratégie est d'environ déjà pour des valeurs modérées de . L'une des raisons pour lesquelles le problème de la secrétaire a reçu tant d'attention est que la politique optimale pour le problème (la règle d'arrêt) est simple et sélectionne le meilleur candidat environ 37% du temps, qu'il y ait 100 ou 100 millions de candidats. ${\style d'affichage 1/e}$${\displaystyle \sim n/e}$${\style d'affichage 1/e}$${\style d'affichage 1/e}$${\style d'affichage n}$

Formulation

Bien qu'il existe de nombreuses variantes, le problème de base peut être énoncé comme suit :

• Il n'y a qu'un seul poste à pourvoir.
• Il y a n candidats pour le poste et la valeur de n est connue.
• Les candidats, s'ils sont vus ensemble, peuvent être classés sans ambiguïté du meilleur au pire.
• Les candidats sont interrogés séquentiellement dans un ordre aléatoire, chaque ordre étant également probable.
• Immédiatement après un entretien, le candidat interrogé est soit accepté, soit rejeté, et la décision est irrévocable.
• La décision d'accepter ou de rejeter un candidat ne peut être fondée que sur les rangs relatifs des candidats interrogés jusqu'à présent.
• L'objectif de la solution générale est d'avoir la probabilité la plus élevée de sélectionner le meilleur candidat de l'ensemble du groupe. Cela revient à maximiser le gain attendu, le gain étant défini comme étant un pour le meilleur candidat et zéro dans le cas contraire.

Un candidat est défini comme un candidat qui, une fois interviewé, est meilleur que tous les candidats interviewés précédemment. Passer est utilisé pour signifier "rejeter immédiatement après l'entretien". Étant donné que l'objectif du problème est de sélectionner le meilleur candidat, seuls les candidats seront pris en compte pour l'acceptation. Le « candidat » dans ce contexte correspond à la notion d'enregistrement en permutation.

Dérivation de la politique optimale

La politique optimale pour le problème est une règle d'arrêt . En vertu de celui-ci, l'intervieweur rejette les premiers r  − 1 candidats (le candidat M est le meilleur candidat parmi ces r  − 1 candidats), puis sélectionne le premier candidat suivant qui est meilleur que le candidat M . On peut montrer que la stratégie optimale réside dans cette classe de stratégies. (Notez que nous ne devrions jamais choisir un candidat qui n'est pas le meilleur que nous ayons vu jusqu'à présent, car il ne peut pas être le meilleur candidat global.) Pour un seuil arbitraire r , la probabilité que le meilleur candidat soit sélectionné est

${\displaystyle {\begin{aligned}P(r)&=\sum _{i=1}^{n}P\left({\text{demandeur }}i{\text{ est sélectionné}}\cap { \text{candidat }}i{\text{ est le meilleur}}\right)\\&=\sum _{i=1}^{n}P\left({\text{candidat }}i{\text { est sélectionné}}|{\text{candidat }}i{\text{ est le meilleur}}\right)\cdot P\left({\text{candidat }}i{\text{ est le meilleur}}\ right)\\&=\left[\sum _{i=1}^{r-1}0+\sum _{i=r}^{n}P\left(\left.{\begin{array} {l}{\text{le meilleur des premiers }}i-1{\text{ candidats}}\\{\text{est dans le premier }}r-1{\text{ candidats}}\end{array }}\right|{\text{candidat }}i{\text{ est le meilleur}}\right)\right]\cdot {\frac {1}{n}}\\&=\left[\sum _ {i=r}^{n}{\frac {r-1}{i-1}}\right]\cdot {\frac {1}{n}}\\&={\frac {r-1} {n}}\sum _{i=r}^{n}{\frac {1}{i-1}}.\end{aligned}}}$

La somme n'est pas définie pour r = 1, mais dans ce cas, la seule politique possible est de sélectionner le premier candidat, et donc P (1) = 1/ n . Cette somme est obtenue en notant que si le candidat i est le meilleur candidat, alors il est sélectionné si et seulement si le meilleur candidat parmi les premiers i  − 1 candidats est parmi les premiers r  − 1 candidats qui ont été rejetés. En laissant n tendre vers l'infini, en écrivant comme la limite de (r-1) / n , en utilisant t pour (i-1) / n et dt pour 1/ n , la somme peut être approchée par l'intégrale ${\style d'affichage x}$

${\displaystyle P(x)=x\int _{x}^{1}{\frac {1}{t}}\,dt=-x\ln(x)\;.}$

En prenant la dérivée de P ( x ) par rapport à , en la fixant à 0 et en résolvant x , nous trouvons que le x optimal est égal à 1/ e . Ainsi, le seuil optimal tend vers n / e lorsque n augmente, et le meilleur candidat est sélectionné avec une probabilité 1/ e . ${\style d'affichage x}$

Pour de petites valeurs de n , le r optimal peut également être obtenu par des méthodes de programmation dynamique standard . Les seuils optimaux r et la probabilité de sélectionner la meilleure alternative P pour plusieurs valeurs de n sont indiqués dans le tableau suivant.

${\style d'affichage n}$	1	2	3	4	5	6	7	8	9
${\style d'affichage r}$	1	1	2	2	3	3	3	4	4
${\style d'affichage P}$	1.000	0,500	0,500	0,458	0,433	0,428	0,414	0,410	0,406

La probabilité de sélectionner le meilleur candidat dans le problème classique de secrétaire converge vers . ${\style d'affichage 1/e\environ 0,368}$

Solution alternative

Ce problème et plusieurs modifications peuvent être résolus (y compris la preuve d'optimalité) de manière directe par l' algorithme des cotes , qui a également d'autres applications. Les modifications du problème de secrétaire qui peuvent être résolues par cet algorithme incluent les disponibilités aléatoires des candidats, des hypothèses plus générales pour les candidats susceptibles d'intéresser le décideur, des entretiens de groupe pour les candidats, ainsi que certains modèles pour un nombre aléatoire de candidats.

Limites

La solution du problème de la secrétaire n'a de sens que s'il est justifié de supposer que les candidats n'ont aucune connaissance de la stratégie de décision employée, car les premiers candidats n'ont aucune chance et peuvent ne pas se présenter autrement.

Un inconvénient important pour les applications de la solution du problème de secrétaire classique est que le nombre de candidats doit être connu à l'avance, ce qui est rarement le cas. Une façon de surmonter ce problème est de supposer que le nombre de candidats est une variable aléatoire avec une distribution connue de (Presman et Sonin, 1972). Cependant, pour ce modèle, la solution optimale est en général beaucoup plus difficile. De plus, la probabilité de réussite optimale n'est désormais plus d'environ 1/ e mais généralement inférieure. Cela peut être compris dans le contexte d'avoir un « prix » à payer pour ne pas connaître le nombre de candidats. Cependant, dans ce modèle, le prix est élevé. Selon le choix de la distribution de , la probabilité de gain optimale peut approcher zéro. La recherche de moyens de faire face à ce nouveau problème a conduit à un nouveau modèle produisant la loi 1/e du meilleur choix. ${\style d'affichage n}$${\style d'affichage N}$${\displaystyle P(N=k)_{k=1,2,\cdots }}$${\style d'affichage N}$

1/e-loi du meilleur choix

L'essence du modèle repose sur l'idée que la vie est séquentielle et que les problèmes du monde réel se posent en temps réel. En outre, il est plus facile d'estimer les moments auxquels des événements spécifiques (arrivées de demandeurs) devraient se produire plus fréquemment (s'ils le font) que d'estimer la distribution du nombre d'événements spécifiques qui se produiront. Cette idée a conduit à l'approche suivante, dite approche unifiée (1984) :

Le modèle est défini comme suit : Un candidat doit être sélectionné à un certain intervalle de temps parmi un nombre inconnu de candidats pouvant être classés. L'objectif est de maximiser la probabilité de ne sélectionner que les meilleurs sous l'hypothèse que tous les ordres d'arrivée de différents rangs sont également probables. Supposons que tous les candidats ont le même, mais indépendante de l'autre, la densité de l' heure d'arrivée sur et laisser indiqueraient la fonction de distribution du temps d'arrivée correspondant, qui est ${\style d'affichage [0,T]}$${\style d'affichage N}$${\style d'affichage f}$${\style d'affichage [0,T]}$${\style d'affichage F}$

${\displaystyle F(t)=\int _{0}^{t}f(s)ds}$, .${\displaystyle \,0\leq t\leq T}$

Soyons tels que Considérez la stratégie d'attendre et d'observer tous les candidats jusqu'à l'heure puis de sélectionner, si possible, le premier candidat après l'heure qui est meilleur que tous les précédents. Alors cette stratégie, appelée 1/e-strategy , a les propriétés suivantes : ${\style d'affichage \tau }$${\displaystyle F(\tau )=1/e.}$${\style d'affichage \tau }$${\style d'affichage \tau }$

La 1/e-stratégie

(i) donne pour tous une probabilité de succès d'au moins 1/e,${\style d'affichage N}$

(ii) est l'unique stratégie garantissant cette probabilité de succès inférieure borne 1/e, et la borne est optimale,

(iii) sélectionne, s'il y a au moins un candidat, aucun avec une probabilité exactement 1/e.

La 1/e-loi, prouvée en 1984 par F. Thomas Bruss , a été une surprise. La raison en était qu'une valeur d'environ 1/e avait été considérée auparavant comme étant hors de portée dans un modèle pour inconnue , alors que cette valeur 1/e était maintenant atteinte comme borne inférieure de la probabilité de succès, et ce dans un modèle avec sans doute des hypothèses beaucoup plus faibles (voir par exemple Math. Reviews 85:m). ${\style d'affichage N}$

La loi 1/e est parfois confondue avec la solution du problème classique de la secrétaire décrite ci-dessus en raison du rôle similaire du nombre 1/e. Cependant, dans la loi 1/e, ce rôle est plus général. Le résultat est également plus fort, puisqu'il est valable pour un nombre inconnu de candidats et que le modèle basé sur une distribution des temps d'arrivée F est plus traitable pour les candidatures.

Le jeu de googol

Selon Ferguson ( 1989 ), le problème de la secrétaire est apparu pour la première fois sous forme imprimée lorsqu'il a été présenté par Martin Gardner dans sa chronique de février 1960 sur les jeux mathématiques dans Scientific American . Voici comment Gardner 1966 l'a formulé : « Demandez à quelqu'un de prendre autant de feuilles de papier qu'il le souhaite, et sur chaque feuillet écrivez un nombre positif différent. Les nombres peuvent aller de petites fractions de 1 à un nombre de la taille d'un googol ( 1 suivi d'une centaine de zéros) ou même plus grand. Ces feuillets sont retournés face cachée et mélangés sur le dessus d'une table. Un à la fois, vous retournez les feuillets face visible. Le but est d'arrêter de tourner lorsque vous arrivez au nombre qui vous devinez être le plus grand de la série. Vous ne pouvez pas revenir en arrière et choisir un feuillet précédemment retourné. Si vous retournez tous les feuillets, alors bien sûr, vous devez choisir le dernier retourné. " erreur harvnb : pas de cible : CITEREFGardner1966 ( aide )

Dans l'article "Qui a résolu le problème du secrétaire ?" Ferguson ( 1989 ) a fait remarquer que le problème de la secrétaire restait sans solution tel qu'il a été exposé par M. Gardner, c'est-à-dire comme un jeu à somme nulle à deux avec deux joueurs antagonistes. Dans ce jeu, Alice, la joueuse avertie, écrit secrètement des nombres distincts sur des cartes. Bob, le joueur qui arrête, observe les valeurs réelles et peut arrêter de tourner les cartes quand il le souhaite, gagnant si la dernière carte tournée a le nombre total maximal. La différence avec le problème de base du secrétaire est que Bob observe les valeurs réelles écrites sur les cartes, qu'il peut utiliser dans ses procédures de décision. Les numéros sur les cartes sont analogues aux qualités numériques des candidats dans certaines versions du problème de secrétaire. La distribution de probabilité conjointe des nombres est sous le contrôle d'Alice. ${\style d'affichage n}$

Bob veut deviner le nombre maximal avec la probabilité la plus élevée possible, tandis que le but d'Alice est de maintenir cette probabilité aussi faible que possible. Il n'est pas optimal pour Alice d'échantillonner les nombres indépendamment d'une distribution fixe, et elle peut mieux jouer en choisissant des nombres aléatoires d'une manière dépendante. Car Alice n'a pas de stratégie minimax , ce qui est étroitement lié à un paradoxe de T. Cover . Mais pour le jeu a une solution : Alice peut choisir des nombres aléatoires (qui sont des variables aléatoires dépendantes) de telle manière que Bob ne puisse pas mieux jouer qu'en utilisant la stratégie d'arrêt classique basée sur les rangs relatifs ( Gnedin 1994 ). ${\style d'affichage n=2}$${\style d'affichage n>2}$

Performance heuristique

La suite de l'article traite à nouveau du problème du secrétariat pour un nombre connu de candidats.

Probabilités de succès attendues pour trois heuristiques.

Stein, Seale & Rapoport 2003 ont dérivé les probabilités de succès attendues pour plusieurs heuristiques psychologiquement plausibles qui pourraient être utilisées dans le problème de la secrétaire. Les heuristiques qu'ils ont examinées étaient les suivantes :

• La règle de coupure (CR): Ne pas accepter l' un des premiers y candidats; par la suite, sélectionnez le premier candidat rencontré (c'est-à-dire un candidat de rang relatif 1). Cette règle a comme cas particulier la politique optimale pour le problème de secrétaire classique pour lequel y  =  r .
• Règle de comptage des candidats (CCR) : sélectionnez le y- ième candidat rencontré. Notez que cette règle n'ignore pas nécessairement les candidats ; il ne considère que le nombre de candidats qui ont été observés, et non la profondeur du décideur dans la séquence des candidats.
• Règle des non-candidats successifs (SNCR) : Sélectionnez le premier candidat rencontré après avoir observé y non-candidats (c'est-à-dire les candidats de rang relatif > 1).

Chaque heuristique a un seul paramètre y . La figure (présentée à droite) affiche les probabilités de succès attendues pour chaque heuristique en fonction de y pour les problèmes avec n  = 80.

Variante de gain cardinale

Trouver le meilleur candidat peut sembler un objectif assez strict. On peut imaginer que l'intervieweur préfère embaucher un candidat de plus grande valeur qu'un autre de moindre valeur, et ne se soucie pas seulement d'obtenir le meilleur. C'est-à-dire que l'intervieweur tirera une certaine valeur de la sélection d'un candidat qui n'est pas nécessairement le meilleur, et la valeur dérivée augmente avec la valeur de celui sélectionné.

Pour modéliser ce problème, supposons que les candidats ont des valeurs « vraies » qui sont des variables aléatoires X tirées iid d'une distribution uniforme sur [0, 1]. Semblable au problème classique décrit ci-dessus, l'enquêteur observe seulement si chaque candidat est le meilleur à ce jour (un candidat), doit accepter ou rejeter chacun sur-le-champ, et doit accepter le dernier s'il est atteint. (Pour être clair, l'intervieweur n'apprend pas le rang relatif réel de chaque candidat. Il apprend seulement si le candidat a le rang relatif 1.) Cependant, dans cette version, le gain est donné par la vraie valeur du candidat sélectionné. Par exemple, s'il sélectionne un candidat dont la vraie valeur est 0,8, il gagnera 0,8. L'objectif de l'intervieweur est de maximiser la valeur attendue du candidat sélectionné. ${\style d'affichage n}$

Étant donné que les valeurs du demandeur sont iid tire d'une distribution uniforme sur [0, 1], la valeur attendue du t ème demandeur donnée qui est donnée par ${\displaystyle x_{t}=\max \left\{x_{1},x_{2},\ldots ,x_{t}\right\}}$

${\displaystyle E_{t}=E\left(X_{t}|I_{t}=1\right)={\frac {t}{t+1}}.}$

Comme dans le problème classique, la politique optimale est donnée par un seuil, que nous désignerons pour ce problème par , auquel l'intervieweur doit commencer à accepter des candidats. Bearden 2006 a montré que c est soit ou . (En fait, celui qui est le plus proche de .) Cela découle du fait que compte tenu d'un problème avec les candidats, le gain attendu pour un seuil arbitraire est ${\style d'affichage c}$${\displaystyle \lfloor {\sqrt {n}}\rfloor }$${\displaystyle \lceil {\sqrt {n}}\rceil }$${\displaystyle {\sqrt {n}}}$${\style d'affichage n}$${\style d'affichage 1\leq c\leq n}$

${\displaystyle V_{n}(c)=\sum _{t=c}^{n-1}\left[\prod _{s=c}^{t-1}\left({\frac {s -1}{s}}\right)\right]\left({\frac {1}{t+1}}\right)+\left[\prod _{s=c}^{n-1}\ gauche({\frac {s-1}{s}}\right)\right]{\frac {1}{2}}={\frac {2cn-{c}^{2}+cn}{2cn} }.}$

En différenciant par rapport à c , on obtient ${\style d'affichage V_{n}(c)}$

${\displaystyle {\frac {\partial V}{\partial c}}={\frac {-{c}^{\,2}+n}{2{c}^{\,2}n}}. }$

Apprentissage dans le paradigme de la recherche séquentielle d'informations partielles. Les nombres affichent les valeurs attendues des candidats en fonction de leur rang relatif (sur le m total des candidats vus jusqu'à présent) à différents moments de la recherche. Les attentes sont calculées en fonction du cas où leurs valeurs sont uniformément réparties entre 0 et 1. Les informations de classement relatif permettent à l'intervieweur d'évaluer plus finement les candidats à mesure qu'ils accumulent plus de points de données pour les comparer.

Puisque pour toutes les valeurs admissibles de , nous trouvons que est maximisé à . Puisque V est convexe dans , le seuil optimal à valeur entière doit être soit ou . Ainsi, pour la plupart des valeurs, l'intervieweur commencera à accepter les candidats plus tôt dans la version à paiement cardinal que dans la version classique où l'objectif est de sélectionner le meilleur candidat. Notez qu'il ne s'agit pas d'un résultat asymptotique : il est valable pour tout . Cependant, ce n'est pas la politique optimale pour maximiser la valeur attendue à partir d'une distribution connue. Dans le cas d'une distribution connue, le jeu optimal peut être calculé via une programmation dynamique. ${\displaystyle \partial ^{\,2}V/\partial c^{\,2}<0}$${\style d'affichage c}$${\style d'affichage V}$${\displaystyle c={\sqrt {n}}}$${\style d'affichage c}$${\displaystyle \lfloor {\sqrt {n}}\rfloor }$${\displaystyle \lceil {\sqrt {n}}\rceil }$${\style d'affichage n}$${\style d'affichage n}$

Une forme plus générale de ce problème introduite par Palley et Kremer (2014) suppose qu'à l'arrivée de chaque nouveau candidat, l'enquêteur observe son rang par rapport à tous les candidats observés précédemment. Ce modèle est cohérent avec la notion d'un intervieweur qui apprend au fur et à mesure qu'il poursuit le processus de recherche en accumulant un ensemble de points de données antérieurs qu'il peut utiliser pour évaluer les nouveaux candidats à leur arrivée. L'un des avantages de ce modèle d'information partielle est que les décisions et les résultats obtenus en fonction des informations relatives au classement relatif peuvent être directement comparés aux décisions et résultats optimaux correspondants si l'intervieweur avait reçu des informations complètes sur la valeur de chaque candidat. Ce problème d'information complète, dans lequel les candidats sont tirés indépendamment d'une distribution connue et l'enquêteur cherche à maximiser la valeur attendue du candidat sélectionné, a été résolu à l'origine par Moser (1956), Sakaguchi (1961) et Karlin (1962).

Autres modifications

Il existe plusieurs variantes du problème de secrétaire qui ont également des solutions simples et élégantes.

Une variante remplace le désir de choisir le meilleur par le désir de choisir le second. Robert J. Vanderbei appelle cela le problème du "postdoc" en faisant valoir que le "meilleur" ira à Harvard. Pour ce problème, la probabilité de réussite pour un nombre pair de candidats est exactement de . Cette probabilité tend vers 1/4 lorsque n tend vers l'infini illustrant le fait qu'il est plus facile de choisir le meilleur que le second. ${\style d'affichage {\frac {0.25n^{2}}{n(n-1)}}}$

Pour une deuxième variante, le nombre de sélections est spécifié supérieur à un. En d'autres termes, l'intervieweur n'embauche pas une seule secrétaire, mais admet plutôt, par exemple, une classe d'étudiants d'un bassin de candidats. Sous l'hypothèse que le succès est atteint si et seulement si tous les candidats sélectionnés sont supérieurs à tous les candidats non sélectionnés, c'est encore un problème qui peut être résolu. Il a été montré dans Vanderbei 1980 que lorsque n est pair et que le désir est de sélectionner exactement la moitié des candidats, la stratégie optimale donne une probabilité de succès de . ${\displaystyle {\frac {1}{n/2+1}}}$

Une autre variante consiste à sélectionner les meilleures secrétaires parmi un pool de , toujours dans un algorithme en ligne. Ceci conduit à une stratégie liée à la classique et au seuil de coupure dont le problème classique est un cas particulier Ghirdar 2009 . ${\style d'affichage k}$${\style d'affichage n}$${\style d'affichage {\frac {0.25n^{2}}{n(n-1)}}}$erreur harvnb : pas de cible : CITEREFGhirdar2009 ( aide )

Problème à choix multiples

Un joueur a le droit de choisir, et il gagne si un choix est le meilleur. Gilbert & Mosteller 1966 ont montré qu'une stratégie optimale est donnée par une stratégie de seuil (stratégie de coupure). Une stratégie optimale appartient à la classe des stratégies définies par un ensemble de nombres seuils , où . Le premier choix doit être utilisé sur les premiers candidats en commençant par le candidat, et une fois le premier choix utilisé, le deuxième choix doit être utilisé sur le premier candidat en commençant par le candidat, et ainsi de suite. ${\style d'affichage r}$${\style d'affichage (a_{1},a_{2},...,a_{r})}$${\displaystyle a_{1}<a_{2}<\cdots <a_{r}}$${\style d'affichage a_{1}}$${\style d'affichage a_{2}}$

Gilbert et Mosteller l'ont montré . Pour d'autres cas qui , voir Matsui & Ano 2016 (par exemple ). ${\displaystyle \left({\frac {a_{1}}{n}},{\frac {a_{2}}{n}},{\frac {a_{3}}{n}},{\ frac {a_{4}}{n}}\right)\rightarrow \left(e^{-1},e^{-{\frac {3}{2}}},e^{-{\frac { 47}{24}}},e^{-{\frac {2761}{1152}}}\right)(n\rightarrow \infty )}$${\style d'affichage r=5,6,...,10}$${\displaystyle {\frac {a_{5}}{n}}\rightarrow e^{-{\frac {4162637}{1474560}}}}$

Quand , la probabilité de gagner converge vers ( Gilbert & Mosteller 1966 ). Matsui & Ano 2016 ont montré que pour tout entier positif , la probabilité de gagner (du problème de secrétaire de choix) converge vers où . Ainsi, la probabilité de gagner converge vers et quand respectivement. ${\style d'affichage r=2}$${\displaystyle e^{-1}+e^{-{\frac {3}{2}}}(n\rightarrow \infty )}$${\style d'affichage r}$${\style d'affichage r}$${\displaystyle p_{1}+p_{2}+\cdots +p_{r}}$${\displaystyle p_{i}=\lim _{n\rightarrow \infty }{\frac {a_{i}}{n}}}$${\displaystyle e^{-1}+e^{-{\frac {3}{2}}}+e^{-{\frac {47}{24}}}}$${\displaystyle e^{-1}+e^{-{\frac {3}{2}}}+e^{-{\frac {47}{24}}}+e^{-{\frac { 2761}{1152}}}}$${\style d'affichage r=3,4}$

Études expérimentales

Des psychologues et des économistes expérimentaux ont étudié le comportement décisionnel de personnes réelles dans des situations problématiques de secrétaire. En grande partie, ce travail a montré que les gens ont tendance à arrêter de chercher trop tôt. Cela peut s'expliquer, au moins en partie, par le coût de l'évaluation des candidats. Dans le monde réel, cela pourrait suggérer que les gens ne recherchent pas suffisamment chaque fois qu'ils sont confrontés à des problèmes où les alternatives de décision sont rencontrées de manière séquentielle. Par exemple, lorsqu'ils essaient de décider à quelle station-service le long d'une autoroute s'arrêter pour faire le plein, les gens peuvent ne pas chercher suffisamment avant de s'arrêter. Si cela est vrai, alors ils auraient tendance à payer plus cher pour l'essence que s'ils avaient cherché plus longtemps. La même chose peut être vraie lorsque les gens recherchent en ligne des billets d'avion. La recherche expérimentale sur des problèmes tels que le problème de la secrétaire est parfois appelée recherche opérationnelle comportementale .

Corrélats neuronaux

Bien qu'il existe un corpus substantiel de recherches en neurosciences sur l'intégration de l'information, ou la représentation de la croyance, dans les tâches de prise de décision perceptive utilisant à la fois des sujets animaux et humains, on sait relativement peu de choses sur la façon dont la décision d'arrêter de collecter des informations est prise.

Les chercheurs ont étudié les bases neuronales de la résolution du problème de secrétaire chez des volontaires sains à l'aide d' une IRM fonctionnelle . Un processus décisionnel de Markov (MDP) a été utilisé pour quantifier la valeur de la poursuite de la recherche par rapport à l'engagement dans l'option actuelle. Les décisions de prendre ou de refuser une option impliquaient les cortex préfrontal pariétal et dorsolatéral , ainsi que le striatum ventral , l'insula antérieure et le cingulaire antérieur . Par conséquent, les régions cérébrales précédemment impliquées dans l'intégration des preuves et la représentation des récompenses codent des franchissements de seuils qui déclenchent des décisions de s'engager dans un choix.

Histoire

Le problème de la secrétaire a apparemment été introduit en 1949 par Merrill M. Flood , qui l'a appelé le problème de la fiancée dans une conférence qu'il a donnée cette année-là. Il l'a mentionné à plusieurs reprises au cours des années 1950, par exemple, lors d'une conférence à Purdue le 9 mai 1958, et il est finalement devenu largement connu dans le folklore bien que rien n'ait été publié à l'époque. En 1958, il envoya une lettre à Leonard Gillman , avec des copies à une douzaine d'amis dont Samuel Karlin et J. Robbins, décrivant une preuve de la stratégie optimale, avec une annexe de R. Palermo qui prouvait que toutes les stratégies sont dominées par une stratégie de la forme "rejeter le premier p inconditionnellement, puis accepter le candidat suivant qui est meilleur". (Voir Déluge (1958).)

La première publication était apparemment de Martin Gardner dans Scientific American, février 1960. Il en avait entendu parler par John H. Fox Jr. et L. Gerald Marnie, qui avaient indépendamment proposé un problème équivalent en 1958 ; ils l'appelaient le "jeu de googol". Fox et Marnie ne connaissaient pas la solution optimale ; Gardner a demandé conseil à Leo Moser , qui (avec JR Pounder) a fourni une analyse correcte pour la publication dans le magazine. Peu de temps après, plusieurs mathématiciens ont écrit à Gardner pour lui parler du problème équivalent qu'ils avaient entendu via la vigne, qui peut très probablement être attribué au travail original de Flood.

La 1/ e -loi du meilleur choix est due à F. Thomas Bruss (1984).

Ferguson (1989) possède une bibliographie étendue et souligne qu'un problème similaire (mais différent) avait été envisagé par Arthur Cayley en 1875 et même par Johannes Kepler bien avant cela.

Généralisation combinatoire

Le problème de la secrétaire peut être généralisé au cas où il y a plusieurs emplois différents. Encore une fois, il y a des candidats qui arrivent dans un ordre aléatoire. Lorsqu'une candidate arrive, elle révèle un ensemble de nombres non négatifs. Chaque valeur spécifie sa qualification pour l'un des emplois. L'administrateur doit non seulement décider d'accepter ou non la candidate mais, dans l'affirmative, doit également l'affecter de façon permanente à l'un des emplois. L'objectif est de trouver une mission où la somme des qualifications est la plus grande possible. Ce problème est identique à la recherche d'une correspondance de poids maximum dans un graphe bipartite à arêtes pondérées où les nœuds d'un côté arrivent en ligne dans un ordre aléatoire. Il s'agit donc d'un cas particulier du problème d' appariement bipartite en ligne . ${\style d'affichage n}$${\style d'affichage n}$

Par une généralisation de l'algorithme classique pour le problème de la secrétaire, il est possible d'obtenir une affectation où la somme attendue des qualifications n'est qu'un facteur inférieur à une affectation optimale (hors ligne). ${\style d'affichage e}$

Voir également

• Problème d'affectation
• Algorithme de cotes
• Arrêt optimal
• Le problème de Robbins
• Théorie de la recherche
• Problème de mariage stable

Remarques

Les références

• Bearden, JN (2006). « Un nouveau problème de secrétaire avec une sélection basée sur le rang et des gains cardinaux ». Journal de psychologie mathématique . 50 : 58-9. doi : 10.1016/j.jmp.2005.11.003 .
• Bearden, JN; Murphy, RO ; Rapoport, A. (2005). « Une extension multi-attributs du problème de secrétaire : théorie et expériences ». Journal de psychologie mathématique . 49 (5) : 410-425. CiteSeerX  10.1.1.497.6468 . doi : 10.1016/j.jmp.2005.08.002 .
• Bearden, J. Neil; Rapoport, Amnon ; Murphy, Ryan O. (septembre 2006). "Observation séquentielle et sélection avec des gains dépendants du rang: une étude expérimentale". Sciences de gestion . 52 (9) : 1437-1449. doi : 10.1287/mnsc.1060.0535 .
• Bruss, F. Thomas (juin 2000). « Sommez les chances à un et arrêtez » . Les Annales des Probabilités . 28 (3) : 1384-1391. doi : 10.1214/aop/1019160340 .
• Bruss, F. Thomas (octobre 2003). "Une note sur les limites du théorème des probabilités d'arrêt optimal" . Les Annales des Probabilités . 31 (4) : 1859-1961. doi : 10.1214/aop/1068646368 .
• Bruss, F. Thomas (août 1984). "Une approche unifiée à une classe de problèmes de meilleur choix avec un nombre inconnu d'options" . Les Annales des Probabilités . 12 (3) : 882-889. doi : 10.1214/aop/1176993237 .

• Freeman, PR (1983). "Le problème du secrétaire et ses extensions : Une revue". Revue Internationale de Statistique / Revue Internationale de Statistique . 51 (2) : 189-206. doi : 10.2307/1402748 . JSTOR  1402748 .
• Girdhar, Yogesh ; Dudek, Grégoire (2009). "Échantillonnage optimal de données en ligne ou comment embaucher les meilleurs secrétaires". 2009 Conférence canadienne sur la vision par ordinateur et robot . p. 292-298. CiteSeerX  10.1.1.161.41 . doi : 10.1109/CRV.2009.30 . ISBN 978-1-4244-4211-9. S2CID  2742443 .
• Gilbert, J; Mosteller, F (1966). "Reconnaître le maximum d'une séquence". Journal de l'Association statistique américaine . 61 (313) : 35-73. doi : 10.2307/2283044 . JSTOR  2283044 .
• Gnedin, A. (1994). "Une solution au jeu de Googol" . Annales de probabilité . 22 (3) : 1588-1595. doi : 10.1214/aop/1176988613 .
• Hill, TP " Savoir quand s'arrêter ". Scientifique américain , Vol. 97, 126-133 (2009). (Pour la traduction française, voir la couverture du numéro de juillet de Pour la Science (2009))
• Ketelaar, Timothée ; Todd, Peter M. (2001). « Encadrer nos pensées : la rationalité écologique en tant que réponse de la psychologie évolutionniste au problème du cadre ». Défis conceptuels en psychologie évolutionniste . Études sur les systèmes cognitifs. 27 . p. 179-211. doi : 10.1007/978-94-010-0618-7_7 . ISBN 978-94-010-3890-4.
• Martin Gardner , New Mathematical Diversions de Scientific American. Simon et Schuster, 1966, chapitre 3, problème 3 [réimprime sa chronique originale publiée en février 1960 avec des commentaires supplémentaires].
• Matsui, T; Ano, K (2016). "Les limites inférieures pour le problème de cotes de Bruss avec plusieurs arrêts". Mathématiques de la recherche opérationnelle . 41 (2) : 700-714. arXiv : 1204.5537 . doi : 10.1287/moor.2015.0748 . S2CID  31778896 .
• Merrill R. Flood, lettre écrite en 1958, dont une copie se trouve dans les papiers de Martin Gardner aux Archives de l'Université de Stanford, série 1, boîte 5, dossier 19.
• Miller, Geoffrey F. (2001). L'esprit d'accouplement : comment le choix sexuel a façonné l'évolution de la nature humaine . Livres d'ancrage. ISBN 978-0-385-49517-2.
• Sardelis, Dimitris A.; Valahas, Theodoros M. (mars 1999). « Prise de décision : une règle d'or ». Le mensuel mathématique américain . 106 (3) : 215. doi : 10.2307/2589677 . JSTOR  2589677 .
• Seale, DA; Rapoport, A. (1997). « Prise de décision séquentielle avec des rangs relatifs : une enquête expérimentale sur le « problème du secrétaire » ». Comportement organisationnel et processus décisionnels humains . 69 (3) : 221-236. doi : 10.1006/obhd.1997.2683 .
• Stein, NOUS ; Seale, DA; Rapoport, A. (2003). "Analyse des solutions heuristiques au problème du meilleur choix". Journal Européen de Recherche Opérationnelle . 151 : 140-152. doi : 10.1016/S0377-2217(02)00601-X .
• Vanderbei, RJ (novembre 1980). « Le choix optimal d'un sous-ensemble d'une population ». Mathématiques de la recherche opérationnelle . 5 (4) : 481-486. doi : 10.1287/moor.5.4.481 .
• Vanderbei, Robert J. (2012). "La variante postdoctorale du problème de la secrétaire" (PDF) . CiteSeerX  10.1.1.366.1718 . Citer le journal nécessite |journal=( aide )

Liens externes

• Séquence OEIS A054404 (Nombre de filles à attendre avant de choisir dans le problème de dot du sultan avec n filles)
• Weisstein, Eric W. "Le problème de la dot du sultan" . MathWorld .
• Neil Bearden. "Recherche optimale (problèmes de secrétaire)" . Archivé de l'original le 4 janvier 2017.
• Livre Optimal Stop and Applications de Thomas S. Ferguson