Slerp - Slerp

En infographie , Slerp est un raccourci pour l'interpolation linéaire sphérique , introduit par Ken Shoemake dans le contexte de l' interpolation quaternion dans le but d' animer la rotation 3D . Il se réfère à un mouvement à vitesse constante le long d'un arc de grand cercle à rayon unitaire , étant donné les extrémités et un paramètre d'interpolation compris entre 0 et 1.

Slerp géométrique

Slerp a une formule géométrique indépendante des quaternions et indépendante de la dimension de l'espace dans lequel l'arc est intégré. Cette formule, somme pondérée symétrique créditée à Glenn Davis, est basée sur le fait que tout point de la courbe doit être une combinaison linéaire des extrémités. Soit p ₀ et p ₁ les premier et dernier points de l'arc, et soit t le paramètre, 0 ≤  t  ≤ 1. Calculez Ω comme l'angle sous-tendu par l'arc, de sorte que cos Ω = p ₀  ∙  p ₁ , le produit scalaire à n dimensions des vecteurs unitaires de l'origine aux extrémités. La formule géométrique est alors

${\ displaystyle \ operatorname {Slerp} (p_ {0}, p_ {1}; t) = {\ frac {\ sin {[(1-t) \ Omega}]} {\ sin \ Omega}} p_ {0 } + {\ frac {\ sin [t \ Omega]} {\ sin \ Omega}} p_ {1}.}$

La symétrie réside dans le fait que . Dans la limite comme Ω → 0, cette formule se réduit à la formule symétrique correspondante pour l'interpolation linéaire , ${\ displaystyle \ operatorname {Slerp} (p_ {0}, p_ {1}; t)}$ ${\ displaystyle = \ operatorname {Slerp} (p_ {1}, p_ {0}; 1-t)}$

${\ displaystyle \ operatorname {Lerp} (p_ {0}, p_ {1}; t) = (1-t) p_ {0} + tp_ {1}. \, \!}$

Un chemin de Slerp est, en fait, l'équivalent en géométrie sphérique d'un chemin le long d'un segment de ligne dans le plan; un grand cercle est une géodésique sphérique .

Le vecteur oblique se redresse au facteur Slerp.

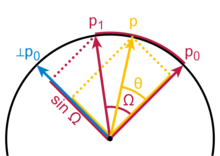
Plus familier que la formule générale de Slerp est le cas où les vecteurs d'extrémité sont perpendiculaires, auquel cas la formule est p ₀  cos  θ + p ₁  sin  θ . En laissant θ = t   π / 2 , et en appliquant l'identité trigonométrique cos  θ = sin ( π / 2 -  θ ) , cela devient la formule de Slerp. Le facteur 1 / sin Ω dans la formule générale est une normalisation, puisqu'un vecteur p ₁ à un angle de Ω à p _{0 se} projette sur la perpendiculaire ⊥ p ₀ avec une longueur de seulement sin Ω .

Certains cas particuliers de Slerp admettent un calcul plus efficace. Lorsqu'un arc de cercle doit être dessiné dans une image raster, la méthode préférée est une variante de l' algorithme de cercle de Bresenham . L'évaluation aux valeurs de paramètres spéciaux 0 et 1 donne trivialement p ₀ et p ₁ , respectivement; et bissection, évaluation à ½, se simplifie en ( p ₀  +  p ₁ ) / 2 , normalisée. Un autre cas particulier, courant dans l'animation, est l'évaluation avec des extrémités fixes et des étapes paramétriques égales. Si p _{k −1} et p _k sont deux valeurs consécutives, et si c est le double de leur produit scalaire (constante pour toutes les étapes), alors la valeur suivante, p _{k +1} , est la réflexion p _{k +1} = c   p _k - p _{k −1} .

Quaternion Slerp

Lorsque Slerp est appliqué à des quaternions unitaires , le chemin du quaternion correspond à un chemin à travers des rotations 3D de manière standard . L'effet est une rotation avec une vitesse angulaire uniforme autour d'un axe de rotation fixe . Lorsque le point final initial est le quaternion d'identité, Slerp donne un segment d'un sous-groupe à un paramètre du groupe de Lie des rotations 3D, SO (3) , et de son groupe de recouvrement universel de quaternions unitaires, S ³ . Slerp donne le chemin le plus droit et le plus court entre ses extrémités de quaternion et correspond à une rotation d'un angle de 2Ω. Cependant, comme le revêtement est double ( q et - q correspondent à la même rotation), la trajectoire de rotation peut tourner soit dans le «chemin court» (moins de 180 °), soit dans le «chemin long» (plus de 180 °). Les longs trajets peuvent être évités en inversant une extrémité si le produit scalaire, cos Ω , est négatif, garantissant ainsi que −90 ° ≤ Ω ≤ 90 °.

Slerp a également des expressions en termes d'algèbre de quaternions, toutes utilisant l' exponentiation . Les puissances réelles d'un quaternion sont définies en termes de la fonction exponentielle du quaternion , écrite comme e ^q et donnée par la série de puissances également familière du calcul, de l'analyse complexe et de l'algèbre matricielle:

${\ displaystyle e ^ {q} = 1 + q + {\ frac {q ^ {2}} {2}} + {\ frac {q ^ {3}} {6}} + \ cdots + {\ frac {q ^ {n}} {n!}} + \ cdots.}$

En écrivant un quaternion unité q sous forme de verseur , cos Ω + v  sin Ω , avec v un vecteur unité 3, et en notant que le carré du quaternion v ² est égal à −1 (impliquant une version quaternion de la formule d' Euler ), nous avons e ^{v  Ω} = q , et q ^t = cos  t  Ω + v  sin  t  Ω  . L'identification d'intérêt est q = q ₁   q ₀ ^-1 , de sorte que la partie réelle de q est cos Ω , le même que le produit scalaire géométrique utilisé ci-dessus. Voici quatre expressions de quaternions équivalentes pour Slerp.

${\ displaystyle {\ begin {aligné} \ operatorname {Slerp} (q_ {0}, q_ {1}, t) & = q_ {0} (q_ {0} ^ {- 1} q_ {1}) ^ { t} \\ [6pt] & = q_ {1} (q_ {1} ^ {- 1} q_ {0}) ^ {1-t} \\ [6pt] & = (q_ {0} q_ {1} ^ {- 1}) ^ {1-t} q_ {1} \\ [6pt] & = (q_ {1} q_ {0} ^ {- 1}) ^ {t} q_ {0} \ end {aligné }}}$

La dérivée de Slerp ( q ₀ ,  q ₁ ;  t ) par rapport à t , en supposant que les extrémités sont fixes, est log ( q ₁ q ₀ ⁻¹ ) fois la valeur de la fonction, où le logarithme naturel du quaternion donne dans ce cas la moitié du Vecteur de vitesse angulaire 3D . Le vecteur tangent initial est transporté parallèlement à chaque tangente le long de la courbe; ainsi la courbe est, en effet, une géodésique.

Dans l' espace tangent en tout point d'une courbe de Slerp à quaternions, l'inverse de la carte exponentielle transforme la courbe en un segment de ligne. Les courbes Slerp ne s'étendant pas à travers un point ne se transforment pas en lignes dans l'espace tangent de ce point.

Les quaternions Slerps sont couramment utilisés pour construire des courbes d'animation lisses en imitant des constructions affines comme l' algorithme de Casteljau pour les courbes de Bézier . Puisque la sphère n'est pas un espace affine , les propriétés familières des constructions affines peuvent échouer, bien que les courbes construites puissent autrement être entièrement satisfaisantes. Par exemple, l'algorithme de Casteljau peut être utilisé pour diviser une courbe dans un espace affine; cela ne fonctionne pas sur une sphère.

Le Slerp à deux valeurs peut être étendu pour interpoler parmi de nombreux quaternions unitaires, mais l'extension perd le temps d' exécution fixe de l'algorithme Slerp.

Les références

Liens externes

• Shoemake, Ken. "Animation de rotation avec des courbes de quaternion" (PDF) . SIGGRAPH 1985.
• Erik B., barrage; Martin, Koch; Lillholm, Martin (17 juillet 1998). "Quaternions, interpolation et animation" (PDF) . Université de Copenhague. Archivé (PDF) de l'original le 2017-08-30.
• Blow, Jonathan (26 février 2004). "Comprendre Slerp, puis ne pas l'utiliser" . Archivé de l'original le 2017-08-25.
• Martin, Brian (23 juin 1999). "Brian Martin sur l'animation Quaternion" . Archivé de l'original le 24/03/2016.