Connexion (faisceau vectoriel) - Connection (vector bundle)
En mathématiques , et notamment en géométrie différentielle et en théorie de jauge , une connexion sur un faisceau de fibres est un dispositif qui définit une notion de transport parallèle sur le faisceau ; c'est-à-dire un moyen de « connecter » ou d'identifier des fibres sur des points voisins. Le cas le plus courant est celui d'une liaison linéaire sur un fibré vectoriel , pour lequel la notion de transport parallèle doit être linéaire . Une connexion linéaire est spécifiée de manière équivalente par une dérivée covariante , un opérateur qui différencie les sections du faisceau le long des directions tangentes dans la variété de base, de telle sorte que les sections parallèles aient une dérivée nulle. Les connexions linéaires généralisent, à des fibrés vectoriels arbitraires, la connexion de Levi-Civita sur le fibré tangent d'une variété pseudo-riemannienne , ce qui donne un moyen standard de différencier les champs de vecteurs. Les connexions non linéaires généralisent ce concept aux faisceaux dont les fibres ne sont pas nécessairement linéaires.
Les connexions linéaires sont également appelées connexions de Koszul d' après Jean-Louis Koszul , qui a donné un cadre algébrique pour les décrire ( Koszul 1950 ).
Cet article définit la connexion sur un fibré vectoriel en utilisant une notation mathématique commune qui désaccentue les coordonnées. Cependant, d'autres notations sont aussi régulièrement utilisées : en relativité générale , les calculs de fibrés vectoriels sont généralement écrits à l'aide de tenseurs indexés ; en théorie de jauge , les endomorphismes des fibres de l'espace vectoriel sont soulignés. Les différentes notations sont équivalentes, comme discuté dans l'article sur les connexions métriques (les commentaires qui y sont faits s'appliquent à tous les fibrés vectoriels).
Motivation
Une section d'un fibré vectoriel généralise la notion de fonction sur une variété, en ce sens qu'une fonction à valeur vectorielle standard peut être considérée comme une section du fibré vectoriel trivial . Il est donc naturel de se demander s'il est possible de différencier une section par analogie à la façon dont on différencie un champ de vecteurs. Lorsque le fibré vectoriel est le fibré tangent à une variété pseudo-riemannienne , cette question est naturellement répondue par la connexion de Levi-Civita , qui est l'unique connexion sans torsion compatible avec la métrique pseudo-riemannienne sur le fibré tangent. En général, il n'y a pas un tel choix naturel d'une manière de différencier les sections.
Le cas modèle est de différencier un champ de vecteurs à -composantes sur l'espace euclidien . Dans ce cadre, la dérivée en un point de la direction peut être simplement définie par
Notez que pour chaque , nous avons défini un nouveau vecteur de sorte que la dérivée de dans la direction de a donné un nouveau champ de vecteurs à composante sur .
En passant à une section d'un fibré vectoriel sur une variété , on rencontre deux problèmes clés avec cette définition. Premièrement, puisque la variété n'a pas de structure linéaire, le terme n'a aucun sens sur . Au lieu de cela, on prend un chemin tel que et calcule
Cependant, cela n'a toujours pas de sens, car est un vecteur dans la fibre sur , et , la fibre sur , qui est un espace vectoriel différent. Cela signifie qu'il n'y a aucun moyen de donner un sens à la soustraction de ces deux termes situés dans des espaces vectoriels différents.
L'objectif est de résoudre l'énigme ci-dessus en trouvant un moyen de différencier les sections d'un fibré vectoriel dans la direction des champs vectoriels, et de récupérer une autre section du fibré vectoriel. Il existe trois solutions possibles à ce problème. Tous les trois nécessitent de faire un choix sur la façon de différencier les sections, et ce n'est que dans des paramètres spéciaux comme le fibré tangent sur une variété riemannienne qu'un tel choix est naturel.
- ( Transport parallèle ) Puisque le problème est que les vecteurs et se trouvent dans des fibres différentes de , une solution consiste à définir un isomorphisme pour tout proche de zéro. En utilisant cet isomorphisme, on peut transporter jusqu'à la fibre et ensuite prendre la différence. Explicitement,C'est le transport parallèle , et le choix des isomorphismes pour toutes les courbes de peut être considéré comme la définition de la façon de différencier une section.
- ( connexion d'Ehresmann ) Utiliser la notion de différentielle d'une application de variétés lisses. Une section est par définition une carte lisse telle que . Celui-ci a un différentiel , avec la propriété que pour un champ vectoriel . Cependant, on aimerait plutôt être une partie de soi. En fait, le faisceau vertical est le retrait de long avec la même fibre . Si l'on choisit une projection de fibrés vectoriels, la composition avec cette projection reviendrait à . C'est ce qu'on appelle une connexion d'Ehresmann linéaire sur le fibré vectoriel . Il existe de nombreux choix d'opérateurs de projection, donc en général, il existe de nombreuses manières différentes de différencier un champ de vecteurs.
- ( Dérivée covariante ) La troisième solution est d'abstraire les propriétés qu'une dérivée d'une section d'un fibré vectoriel devrait avoir et de la prendre comme définition axiomatique. C'est la notion de connexion ou de dérivée covariante décrite dans cet article. On peut montrer que les deux autres approches ci-dessus sont équivalentes à cette définition axiomatique de la différenciation.
Définition formelle
Soit un fibré vectoriel lisse sur une variété différentiable . Notons l'espace des sections lisses de par . Une connexion en est un - linéaire (ou lorsque le faisceau de vecteur est un paquet vectoriel complexe , une carte -linéaire)
telle que la règle de Leibniz
est valable pour toutes les fonctions lisses sur et toutes les sections lisses de .
Si est un champ de vecteurs tangent sur (c'est-à-dire une section du fibré tangent ) on peut définir une dérivée covariante le long de
en contractant avec l'indice covariant résultant dans la connexion : . La dérivée covariante vérifie :
Inversement, tout opérateur satisfaisant aux propriétés ci-dessus définit une connexion sur et une connexion dans ce sens est également connue sous le nom de dérivée covariante sur .
Connexions induites
Étant donné un fibré vectoriel , il existe de nombreux fibrés associés auxquels on peut construire , par exemple le fibré vectoriel double , les puissances tensorielles , les puissances tensorielles symétriques et antisymétriques , et les sommes directes . Une connexion sur induit une connexion sur l'un quelconque de ces faisceaux associés. La facilité de passage entre les connexions sur les faisceaux associés est plus élégamment capturée par la théorie des connexions de faisceaux principaux , mais nous présentons ici quelques-unes des connexions induites de base.
Double connexion
Étant donné une connexion sur , la connexion double induite sur est définie implicitement par
Voici un champ vectoriel lisse, est une section de , et une section du fibré dual, et l'appariement naturel entre un espace vectoriel et son dual (se produisant sur chaque fibre entre et ). Notez que cette définition applique essentiellement cette connexion afin qu'une règle de produit naturel soit satisfaite pour l'appariement .
Connexion produit tenseur
Étant donné les connexions sur deux fibrés vectoriels , définissez la connexion du produit tensoriel par la formule
Ici, nous avons . Notez encore une fois que c'est la manière naturelle de combiner pour appliquer la règle de produit pour la connexion de produit tensoriel. Par application répétée de la construction ci - dessus appliquée au produit tensoriel , on obtient également la connexion de puissance du tenseur sur pour tout et vecteur faisceau .
Connexion à somme directe
La connexion à somme directe est définie par
où .
Connexions électriques symétriques et extérieures
Puisque la puissance symétrique et la puissance extérieure d'un fibré vectoriel peuvent être considérées naturellement comme des sous-espaces de la puissance tensorielle, , la définition de la connexion du produit tensoriel s'applique de manière directe à ce paramètre. En effet, puisque les algèbres symétriques et extérieures se trouvent à l'intérieur de l' algèbre tensorielle en tant que sommations directes, et que la connexion respecte cette division naturelle, on peut simplement se limiter à ces sommations. Explicitement, définissez la connexion de produit symétrique en
et le raccordement extérieur du produit par
pour tous . Des applications répétées de ces produits donne induit la puissance symétrique et les connexions électriques extérieures sur et respectivement.
Connexion endomorphisme
Enfin, on peut définir la connexion induite sur le faisceau vectoriel d'endomorphismes , la connexion d'endomorphisme . Il s'agit simplement de la connexion du produit tenseur de la connexion double sur et sur . Si et , de sorte que la composition aussi, alors la règle de produit suivante est valable pour la connexion d'endomorphisme :
En inversant cette équation, il est possible de définir la connexion d'endomorphisme comme la connexion unique satisfaisant
pour tout , évitant ainsi d'avoir à définir au préalable la double connexion et la connexion du produit tenseur.
Tout forfait associé
Étant donné un fibré vectoriel de rang , et toute représentation dans un groupe linéaire , il existe une connexion induite sur le fibré vectoriel associé . Cette théorie est capturée de la manière la plus succincte en passant à la connexion du faisceau principal sur le faisceau de trame et en utilisant la théorie des faisceaux principaux. Chacun des exemples ci-dessus peut être vu comme des cas particuliers de cette construction : le fibré dual correspond à la représentation inverse transposée (ou inverse adjointe), le produit tensoriel à la représentation tensorielle du produit, la somme directe à la représentation directe somme, et ainsi de suite au.
Dérivée covariante extérieure et formes vectorielles
Soit un fibré vectoriel. Une forme différentielle de degré est une section du fibré produit tensoriel :
L'espace de telles formes est désigné par
où le dernier produit tensoriel désigne le produit tensoriel des modules sur l' anneau des fonctions lisses sur .
Une forme de valeur 0 n'est qu'une section du bundle . C'est-à-dire,
Dans cette notation, une connexion sur est une application linéaire
Une connexion peut alors être considérée comme une généralisation de la dérivée extérieure aux formes valorisées par faisceau vectoriel. En fait, étant donné une connexion sur il existe un moyen unique d'étendre à une dérivée covariante extérieure
Cette dérivée covariante extérieure est définie par la règle de Leibniz suivante, qui est spécifiée sur des tenseurs simples de la forme et étendue linéairement :
où so that , est une section et désigne la forme - avec des valeurs dans définies par calage avec la partie monoforme de . Notez que pour les formes 0, cela récupère la règle Leibniz normale pour la connexion .
Contrairement à la dérivée extérieure ordinaire, on a généralement . En fait, est directement liée à la courbure de la connexion (voir ci - dessous ).
Propriétés affines de l'ensemble des connexions
Tout fibré vectoriel sur une variété admet une connexion, qui peut être prouvée en utilisant des partitions d'unité . Cependant, les connexions ne sont pas uniques. Si et sont deux connexions, alors leur différence est un opérateur linéaire. C'est-à-dire,
pour toutes les fonctions lisses sur et toutes les sections lisses de . Il s'ensuit que la différence peut être identifiée de manière unique avec une forme unique avec des valeurs dans le fibré d'endomorphisme :
Inversement, si est une connexion sur et est une forme unique sur avec des valeurs dans , alors est une connexion sur .
En d'autres termes, l'espace des connexions sur est un espace affine pour . Cet espace affine est communément noté .
Relation avec les connexions principales et Ehresmann
Soit un fibré vectoriel de rang et soit le fibré principal de . Ensuite, une connexion (principale) sur induit une connexion sur . Tout d'abord, notez que les sections de sont en correspondance un à un avec les cartes équivariantes à droite . (Ceci peut être vu en considérant le retrait de over , qui est isomorphe au fibré trivial .) Étant donné une section de laissez l'application équivariante correspondante être . La dérivée covariante sur est alors donnée par
où est l' élévation horizontale de de à . (Rappelez-vous que la levée horizontale est déterminée par la connexion sur .)
Inversement, une connexion sur détermine une connexion sur , et ces deux constructions sont réciproquement inverses.
Une connexion sur est également déterminée de manière équivalente par une connexion linéaire d'Ehresmann sur . Cela fournit une méthode pour construire la connexion principale associée.
Les connexions induites décrites dans #Connexions induites peuvent être construites en tant que connexions sur d'autres faisceaux associés au faisceau de trames de , en utilisant des représentations autres que la représentation standard utilisée ci-dessus. Par exemple, si désigne la représentation standard de on , alors le fibré associé à la représentation de on est le fibré somme directe , et la connexion induite est précisément celle qui a été décrite ci-dessus.
Expression locale
Soit un fibré vectoriel de rang , et soit un ouvert de sur lequel se banalise. Donc sur l'ensemble , admet un cadre lisse local de sections
Puisque le cadre définit une base de la fibre pour tout , on peut étendre n'importe quelle section locale dans le cadre comme
pour une collection de fonctions lisses .
Étant donné une connexion sur , il est possible d'exprimer sur en termes de repère local de sections, en utilisant la règle de produit caractéristique de la connexion. Pour toute section de base , la quantité peut être augmentée dans le cadre local comme
où se trouvent une collection de formes uniques locales. Ces formes peuvent être mises dans une matrice de formes uniques définies par
appelé la forme de connexion locale de plus . L'action de sur n'importe quelle section peut être calculée en utilisant la règle du produit comme
Si la section locale est également écrite en notation matricielle sous forme de vecteur colonne en utilisant le référentiel local comme base,
puis en utilisant une multiplication matricielle régulière, on peut écrire
où est un raccourci pour appliquer la dérivée extérieure à chaque composante de en tant que vecteur colonne. Dans cette notation, on écrit souvent localement que . En ce sens, une connexion est localement complètement spécifiée par sa forme unique de connexion dans une certaine banalisation.
Comme expliqué dans les propriétés #Affine de l'ensemble de connexions , toute connexion diffère d'une autre par une forme unique à valeur d'endomorphisme. De ce point de vue, la forme unique de connexion est précisément la forme unique à valeur d'endomorphisme telle que la connexion sur diffère de la connexion triviale sur , qui existe car est un ensemble de trivialisation pour .
Relation avec les symboles Christoffel
Dans la géométrie pseudo-riemannienne , la connexion Levi-Civita est souvent écrite en termes de symboles de Christoffel au lieu de la connexion une forme . Il est possible de définir des symboles de Christoffel pour une connexion sur n'importe quel fibré vectoriel, et pas seulement le fibré tangent d'une variété pseudo-riemannienne. Pour ce faire, supposons qu'en plus d' être un sous-ensemble ouvert banalisant pour le fibré vectoriel , c'est aussi un graphe local pour la variété , admettant des coordonnées locales .
Dans un tel graphique local, il existe un cadre local distinct pour les formes uniques différentielles données par , et les formes uniques de connexion locale peuvent être développées sur cette base comme
pour une collection de fonctions lisses locales , appelées symboles de Christoffel de plus . Dans le cas où et est la connexion Levi-Civita, ces symboles concordent précisément avec les symboles de Christoffel de la géométrie pseudo-riemannienne.
L'expression de la façon dont agit dans les coordonnées locales peut être encore développée en termes de carte locale et des symboles de Christoffel, à donner par
Contracter cette expression avec le vecteur tangent de coordonnées locales conduit à
Cela définit une collection d' opérateurs définis localement
avec la propriété qui
Changement de banalisation locale
Supposons qu'il existe un autre choix de référentiel local sur le même ensemble de trivialisation , de sorte qu'il existe une matrice de fonctions lisses relatives et , définie par
En retraçant la construction de la forme de connexion locale pour le cadre , on trouve que la forme unique de connexion pour est donnée par
où désigne la matrice inverse à . En notation matricielle, cela peut s'écrire
où est la matrice des monoformes donnée en prenant la dérivée extérieure de la matrice composant par composant.
Dans le cas où est le fibré tangent et est le jacobien d'une transformation coordonnée de , les longues formules pour la transformation des symboles de Christoffel de la connexion Levi-Civita peuvent être récupérées à partir des lois de transformation plus succinctes de la forme de connexion ci-dessus.
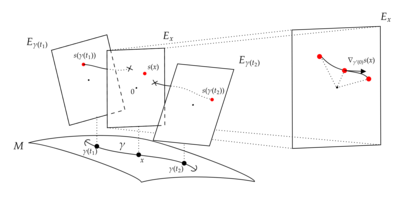
Transport parallèle et holonomie
Une connexion sur un fibré vectoriel définit une notion de transport parallèle le long d'une courbe dans . Soit un chemin en douceur dans . Une section de long est dite parallèle si
pour tous . De manière équivalente, on peut considérer le paquet de retrait de by . Il s'agit d'un faisceau vectoriel avec fibre sur . La connexion sur tire vers une connexion sur . Une section de est parallèle si et seulement si .
Supposons qu'il s'agisse d' un chemin de à dans . L'équation ci-dessus définissant les sections parallèles est une équation différentielle ordinaire du premier ordre (cf. expression locale ci-dessus) et a donc une solution unique pour chaque condition initiale possible. C'est-à-dire que pour chaque vecteur dans il existe une section parallèle unique de avec . Définir une carte de transport parallèle
par . On peut montrer qu'il s'agit d'un isomorphisme linéaire , dont l'inverse est donné en suivant la même procédure avec le chemin inverse de à .
Le transport parallèle peut être utilisé pour définir le groupe d'holonomie de la connexion basée sur un point dans . C'est le sous-groupe constitué de toutes les cartes de transport parallèles provenant de boucles basées à :
Le groupe d'holonomie d'une connexion est intimement lié à la courbure de la connexion ( AmbroseSinger 1953 ).
La connexion peut être récupérée auprès de ses opérateurs de transport parallèles comme suit. Si est un champ vectoriel et une section, en un point, choisissez une courbe intégrale pour à . Pour chacun, nous écrirons pour la carte de transport parallèle voyageant de à . En particulier pour chaque , nous avons . Ensuite , définit une courbe dans l'espace vectoriel , qui peut être différenciée. La dérivée covariante est récupérée comme
Cela démontre qu'une définition équivalente d'une connexion est donnée en spécifiant tous les isomorphismes de transport parallèles entre les fibres de et en prenant l'expression ci-dessus comme définition de .
Courbure
La courbure d'une connexion sur est une 2-forme sur avec des valeurs dans le fibré d'endomorphisme . C'est-à-dire,
Il est défini par l'expression
où et sont des champs de vecteurs tangents sur et est une section de . Il faut vérifier que est -linéaire dans les deux et et qu'il définit en fait un endomorphisme fibré de .
Comme mentionné ci - dessus , la dérivée extérieure covariante n'a pas besoin d'être carrée à zéro lorsqu'elle agit sur des formes à valeurs. L'opérateur est cependant strictement tensoriel (ie -linéaire). Cela implique qu'il est induit à partir d'une 2-forme avec des valeurs dans . Cette 2-forme est précisément la forme de courbure donnée ci-dessus. Pour une forme -valuée, nous avons
Une connexion plate est une connexion dont la forme de courbure disparaît à l'identique.
Forme locale et équation de la structure de Cartan
La forme de courbure a une description locale appelée équation de structure de Cartan . Si a une forme locale sur un sous-ensemble ouvert banalisant pour , alors
sur . Pour clarifier cette notation, notez qu'il s'agit d'une forme unique à valeur d'endomorphisme, et donc en coordonnées locales prend la forme d'une matrice de formes uniques. L'opération applique la dérivée extérieure composante par composante à cette matrice, et dénote une multiplication matricielle, où les composantes sont calées plutôt que multipliées.
En coordonnées locales sur au dessus , si la forme de connexion est écrite pour une collection d' endomorphismes locaux , alors on a
En élargissant encore cela en termes de symboles de Christoffel, on obtient l'expression familière de la géométrie riemannienne. À savoir si est une section de plus de , alors
Voici le tenseur de courbure complet de , et en géométrie riemannienne serait identifié avec le tenseur de courbure riemannienne .
On peut vérifier que si nous définissons comme étant un produit en coin de formes mais un commutateur d'endomorphismes par opposition à la composition, alors , et avec cette notation alternative l'équation de structure de Cartan prend la forme
Cette notation alternative est couramment utilisée dans la théorie des connexions de fibrés principaux, où à la place nous utilisons une forme de connexion , une forme unique d' algèbre de Lie , pour laquelle il n'y a pas de notion de composition (contrairement au cas des endomorphismes), mais il y a est une notion de parenthèse de Lie.
Dans certaines références (voir par exemple ( MadsenTornehave1997 )) l'équation de la structure de Cartan peut être écrite avec un signe moins :
Cette convention différente utilise un ordre de multiplication matricielle différent de la notation Einstein standard dans le produit en coin des formes uniques à valeur matricielle.
Identité Bianchi
Une version de la seconde identité (différentielle) de Bianchi de la géométrie riemannienne est valable pour une connexion sur n'importe quel fibré vectoriel. Rappelons qu'une connexion sur un fibré vectoriel induit une connexion d'endomorphisme sur . Cette connexion d'endomorphisme a elle-même une dérivée covariante extérieure, que nous appelons de manière ambiguë . Puisque la courbure est une forme à deux valeurs définie globalement , nous pouvons lui appliquer la dérivée covariante extérieure. L' identité Bianchi dit que
- .
Cela capture succinctement les formules tensorielles compliquées de l'identité de Bianchi dans le cas des variétés riemanniennes, et on peut traduire cette équation aux identités de Bianchi standard en développant la connexion et la courbure en coordonnées locales.
Il n'y a pas d'analogue en général de la première identité (algébrique) de Bianchi pour une connexion générale, car cela exploite les symétries spéciales de la connexion Levi-Civita. À savoir, on exploite le fait que les indices de faisceaux vectoriels du tenseur de courbure peuvent être échangés avec les indices de faisceaux cotangents provenant d' après avoir utilisé la métrique pour abaisser ou augmenter les indices. Par exemple, cela permet de définir la condition d'absence de torsion pour la connexion Levi-Civita, mais pour un faisceau vectoriel général, l' indice fait référence à la base de coordonnées locale de , et les indices au référentiel local de et provenant de la fractionnement . Cependant dans des circonstances particulières, par exemple lorsque le rang de est égal à la dimension de et qu'une forme de soudure a été choisie, on peut utiliser la soudure pour intervertir les indices et définir une notion de torsion pour les connexions affines qui ne sont pas la connexion Levi-Civita.
Transformations de jauge
Étant donné deux connexions sur un fibré vectoriel , il est naturel de se demander quand elles peuvent être considérées comme équivalentes. Il existe une notion bien définie d' automorphisme d'un fibré vectoriel . Une section est un automorphisme si est inversible en tout point . Un tel automorphisme est appelé une transformation de jauge de , et le groupe de tous les automorphismes est appelé le groupe de jauge , souvent noté ou . Le groupe de transformations de jauge peut être nettement caractérisé comme l'espace des sections du fibré adjoint A majuscule du fibré de trame du fibré vectoriel . Ceci ne doit pas être confondu avec la minuscule a fibré adjoint , qui s'identifie naturellement à lui-même. Le faisceau est le faisceau associé au faisceau de trame principal par la représentation de conjugaison de sur lui-même, , et a fibre le même groupe linéaire général où . Notez que bien qu'il ait la même fibre que le faisceau de trame et qu'il lui soit associé, il n'est pas égal au faisceau de trame, ni même à un faisceau principal lui-même. Le groupe de jauges peut être caractérisé de manière équivalente comme
Une transformation de jauge agit sur les sections , et agit donc sur les liaisons par conjugaison. Explicitement, si est une connexion sur , alors on définit par
pour . Pour vérifier qu'il s'agit d'une connexion, on vérifie la règle du produit
On peut vérifier que cela définit une action de groupe à gauche sur l'espace affine de toutes les connexions .
Puisque est un espace affine modélisé sur , il devrait exister une forme unique à valeur d'endomorphisme telle que . En utilisant la définition de la connexion d'endomorphisme induite par , on peut voir que
c'est-à-dire que .
Deux connexions sont dites équivalentes de jauge si elles diffèrent par l'action du groupe de jauge, et l'espace quotient est l' espace des modules de toutes les connexions sur . En général, cet espace topologique n'est ni une variété lisse ni même un espace de Hausdorff , mais contient à l'intérieur l' espace des modules des connexions de Yang-Mills sur , ce qui présente un intérêt significatif en théorie de jauge et en physique .
Exemples
- Une dérivée covariante classique ou connexion affine définit une connexion sur le fibré tangent de M , ou plus généralement sur tout fibré tensoriel formé en prenant les produits tensoriels du fibré tangent avec lui-même et son dual.
- Une connexion sur peut être décrite explicitement comme l'opérateur
- où est la dérivée extérieure évaluée sur les fonctions lisses à valeurs vectorielles et sont lisses. Une section peut être identifiée avec une carte
- puis
- Si le faisceau est doté d'une métrique de faisceau , un produit interne sur ses fibres d'espace vectoriel, une connexion métrique est définie comme une connexion compatible avec la métrique de faisceau.
- Une connexion de Yang-Mills est une connexion métrique spéciale qui satisfait les équations du mouvement de Yang-Mills .
- Une connexion riemannienne est une connexion métrique sur le fibré tangent d'une variété riemannienne .
- Une connexion Levi-Civita est une connexion riemannienne spéciale : la connexion compatible métrique sur le faisceau tangent qui est également sans torsion . Elle est unique, dans le sens où étant donné toute connexion riemannienne, on peut toujours trouver une et une seule connexion équivalente sans torsion. « Équivalent » signifie qu'il est compatible avec la même métrique, bien que les tenseurs de courbure puissent être différents ; voir téléparallélisme . La différence entre une connexion riemannienne et la connexion de Levi-Civita correspondante est donnée par le tenseur de contorsion .
- La dérivée extérieure est une connexion plate sur (le fibré trivial sur M ).
- Plus généralement, il existe une connexion plate canonique sur tout fibré vectoriel plat (c'est-à-dire un fibré vectoriel dont les fonctions de transition sont toutes constantes) qui est donnée par la dérivée extérieure dans toute banalisation.
Voir également
Les références
- Chern, Shiing-Shen (1951), Topics in Differential Geometry , Institute for Advanced Study, notes de cours polycopiés
- Darling, RWR (1994), Differential Forms and Connections , Cambridge, Royaume-Uni : Cambridge University Press, ISBN 0-521-46800-0
- Kobayashi, Shoshichi ; Nomizu, Katsumi (1996) [1963], Fondements de la géométrie différentielle , Vol. 1 , Wiley Classics Library, New York : Wiley Interscience , ISBN 0-471-15733-3
- Koszul, JL (1950), « Homologie et cohomologie des algèbres de Lie », Bulletin de la Société Mathématique , 78 : 65-127
- Wells, RO (1973), Analyse différentielle sur les variétés complexes , Springer-Verlag, ISBN 0-387-90419-0
- Ambroise, W. ; Singer, IM (1953), "A theorem on holonomy", Transactions of the American Mathematical Society , 75 : 428-443, doi : 10.2307/1990721
- Donaldson, SK et Kronheimer, PB, 1997. La géométrie des quatre variétés. Presses de l'Université d'Oxford.
- Tu, LW, 2017. Géométrie différentielle : connexions, courbure et classes caractéristiques (Vol. 275). Springer.
- Taubes, CH, 2011. Géométrie différentielle : Faisceaux, connexions, métriques et courbure (Vol. 23). OUP Oxford.
- Lee, JM, 2018. Introduction aux variétés riemanniennes. Éditions internationales Springer.
- Madsen, IH ; Tornehave, J. (1997), Du calcul à la cohomologie : cohomologie de Rham et classes caractéristiques , Cambridge University Press



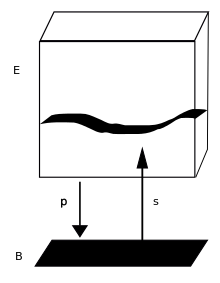






































































































































































![{\displaystyle \gamma :[0,1]\to M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0066953642fb00abb394327531cea098815cd1c8)

![t\dans [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)

![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)






















![{\displaystyle F_{\nabla }(X,Y)(s)=\nabla _{X}\nabla _{Y}s-\nabla _{Y}\nabla _{X}s-\nabla _{[ X,Y]}s}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f59042b065edd05300ca109d93fe0d5b9537b96d)










![{\displaystyle F_{\nabla }=\sum _{p,q=1}^{n}{\frac {1}{2}}\left({\frac {\partial A_{q}}{\partial x^{p}}}-{\frac {\partial A_{p}}{\partial x^{q}}}+[A_{p},A_{q}]\right)dx^{p}\ coin dx^{q}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45e8d584b3732866710e9d1a066d866c42bb633)




![{\style d'affichage [A,A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b8f9de22f28fafb483e8f47e20ca0046206b5e6)
![{\displaystyle A\wedge A={\frac {1}{2}}[A,A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/793044c51a2a65137eaec786a1e6842bdc89b11c)
![{\displaystyle F_{\nabla }=dA+{\frac {1}{2}}[A,A].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a8d81a9efc378e6914d6e299fcfae517ec64c39)






































