Carte équivariante - Equivariant map
En mathématiques , l' équivariance est une forme de symétrie pour les fonctions d'un espace avec symétrie à un autre (comme les espaces symétriques ). Une fonction est dite équivariante lorsque son domaine et son codomaine sont sollicités par le même groupe de symétrie , et lorsque la fonction commute avec l'action du groupe. C'est-à-dire que l'application d'une transformation de symétrie puis le calcul de la fonction produisent le même résultat que le calcul de la fonction puis l'application de la transformation.
Les cartes équivariantes généralisent le concept d' invariants , fonctions dont la valeur est inchangée par une transformation de symétrie de leur argument. La valeur d'une application équivariante est souvent (imprécisément) appelée un invariant.
Dans l'inférence statistique , l'équivariance sous les transformations statistiques des données est une propriété importante de diverses méthodes d'estimation ; voir estimateur invariant pour plus de détails. En mathématiques pures, l'équivariance est un objet d'étude central en topologie équivariante et ses sous-thèmes cohomologie équivariante et théorie d'homotopie stable équivariante .
Exemples
Géométrie élémentaire

Dans la géométrie des triangles , l' aire et le périmètre d'un triangle sont invariants : la translation ou la rotation d'un triangle ne modifie pas son aire ou son périmètre. Cependant, les centres de triangle , comme le centre de gravité , circumcenter , incenter et orthocenter ne sont pas invariantes, car le déplacement d' un triangle aussi en sorte que ses centres de se déplacer. Au lieu de cela, ces centres sont équivariants : appliquer n'importe quelle congruence euclidienne (une combinaison d'une translation et d'une rotation) à un triangle, puis construire son centre, produit le même point que de construire d'abord le centre, puis d'appliquer la même congruence au centre. Plus généralement, tous les centres des triangles sont également équivariants sous les transformations de similarité (combinaisons de translation, rotation et mise à l'échelle), et le centre de gravité est équivariant sous les transformations affines .
La même fonction peut être un invariant pour un groupe de symétries et équivariant pour un groupe différent de symétries. Par exemple, sous des transformations de similarité au lieu de congruences, l'aire et le périmètre ne sont plus invariants : la mise à l'échelle d'un triangle change également son aire et son périmètre. Cependant, ces changements se produisent de manière prévisible : si un triangle est mis à l'échelle d'un facteur s , le périmètre est également mis à l'échelle de s et l'aire est mise à l'échelle de s 2 . De cette façon, la fonction mappant chaque triangle à son aire ou à son périmètre peut être considérée comme équivariante pour une action de groupe multiplicative des transformations d'échelle sur les nombres réels positifs.
Statistiques
Une autre classe d'exemples simples provient de l'estimation statistique . La moyenne d'un échantillon (un ensemble de nombres réels) est couramment utilisée comme tendance centrale de l'échantillon. Il est équivariant sous les transformations linéaires des nombres réels, donc par exemple il n'est pas affecté par le choix des unités utilisées pour représenter les nombres. En revanche, la moyenne n'est pas équivariante par rapport aux transformations non linéaires telles que les exponentielles.
La médiane d'un échantillon est équivariante pour un groupe beaucoup plus large de transformations, les fonctions (strictement) monotones des nombres réels. Cette analyse indique que la médiane est plus robuste contre certains types de modifications d'un ensemble de données et que (contrairement à la moyenne) elle est significative pour les données ordinales .
Les concepts d' estimateur invariant et d' estimateur équivariant ont été utilisés pour formaliser ce style d'analyse.
Théorie des représentations
Dans la théorie des représentations des groupes finis , un espace vectoriel équipé d'un groupe qui agit par transformations linéaires de l'espace est appelé une représentation linéaire du groupe. Une carte linéaire qui commute avec l'action est appelée un entrelacement . C'est-à-dire qu'un entrelacement n'est qu'une application linéaire équivariante entre deux représentations. Alternativement, un entrelacement pour les représentations d'un groupe G sur un corps K est la même chose qu'un homomorphisme de module de K [ G ] - modules , où K [ G ] est l' anneau de groupe de G .
Sous certaines conditions, si X et Y sont tous deux des représentations irréductibles , alors un entrelacement (autre que la carte zéro ) n'existe que si les deux représentations sont équivalentes (c'est-à-dire isomorphes en tant que modules ). Cet entrelacement est alors unique à un facteur multiplicatif près (un scalaire non nul de K ). Ces propriétés sont valables lorsque l'image de K [ G ] est une algèbre simple, de centre K (par ce qu'on appelle le lemme de Schur : voir module simple ). En conséquence, dans les cas importants, la construction d'un entrelacement suffit à montrer que les représentations sont effectivement les mêmes.
Formalisation
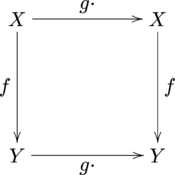
L'équivariance peut être formalisée en utilisant le concept d'un G -set pour un groupe G . Il s'agit d'un objet mathématique constitué d'un ensemble mathématique S et d'une action de groupe (à gauche) de G sur S . Si X et Y sont tous deux des G -ensembles pour le même groupe G , alors une fonction f : X → Y est dite équivariante si
- f ( g · x ) = g · f ( x )
pour tout g ∈ G et tout x dans X .
Si l'une des actions ou les deux sont des actions correctes, la condition d'équivariance peut être modifiée de manière appropriée :
- f ( x · g ) = f ( x ) · g ; (droite-droite)
- f ( x · g ) = g -1 · f ( x ) ; (droite gauche)
- f ( g · x ) = f ( x )· g -1 ; (gauche droite)
Les applications équivariantes sont des homomorphismes dans la catégorie des G -sets (pour un G fixé ). Par conséquent, ils sont également connus sous le nom de G- morphismes , G- maps ou G- homomorphismes . Les isomorphismes des G -sets sont simplement des applications équivariantes bijectives .
La condition d'équivariance peut également être comprise comme le diagramme commutatif suivant . Notez que désigne la carte qui prend un élément et renvoie .
Généralisation
Les cartes équivariantes peuvent être généralisées à des catégories arbitraires de manière simple. Chaque groupe G peut être considéré comme une catégorie avec un seul objet (les morphismes de cette catégorie ne sont que les éléments de G ). Étant donnée une catégorie arbitraire C , une représentation de G dans la catégorie C est un foncteur de G vers C . Un tel foncteur sélectionne un objet de C et un sous - groupe d' automorphismes de cet objet. Par exemple, un G -set est équivalent à un foncteur de G à la catégorie des ensembles , Set , et une représentation linéaire est équivalente à un foncteur à la catégorie des espaces vectoriels sur un champ, Vect K .
Étant donné deux représentations, ρ et σ, de G dans C , une application équivariante entre ces représentations est simplement une transformation naturelle de ρ en σ. En utilisant les transformations naturelles comme morphismes, on peut former la catégorie de toutes les représentations de G dans C . C'est juste la catégorie de foncteur C G .
Pour un autre exemple, prenons C = Top , la catégorie des espaces topologiques . Une représentation de G dans Top est un espace topologique sur lequel G agit en continu . Une application équivariante est alors une application continue f : X → Y entre représentations qui commute avec l'action de G .
Voir également
- Théorème de Curtis–Hedlund–Lyndon , une caractérisation des automates cellulaires en termes de cartes équivariantes