Propriété de borne supérieure - Least-upper-bound property

Chaque sous-ensemble non vide des nombres réels qui est borné par le haut a une borne supérieure minimale.${\style d'affichage M}$${\displaystyle \mathbb {R} }$

En mathématiques , la propriété de la limite supérieure (parfois appelée complétude ou propriété supremum ou propriété lub ) est une propriété fondamentale des nombres réels . Plus généralement, un ensemble partiellement ordonné X a la propriété de borne supérieure la moins élevée si chaque sous- ensemble non vide de X avec une borne supérieure a une borne supérieure minimale (supremum) dans X . Tous les ensembles (partiellement) ordonnés n'ont pas la propriété de limite supérieure la moins élevée. Par exemple, l'ensemble de tous les nombres rationnels avec son ordre naturel n'a pas la moindre propriété de borne supérieure. ${\displaystyle \mathbb {Q} }$

La propriété de la limite supérieure la moins élevée est une forme de l' axiome de complétude pour les nombres réels, et est parfois appelée complétude de Dedekind . Il peut être utilisé pour prouver de nombreux résultats fondamentaux de l'analyse réelle , tels que le théorème des valeurs intermédiaires , le théorème de Bolzano-Weierstrass , le théorème des valeurs extrêmes et le théorème de Heine-Borel . Il est généralement considéré comme un axiome dans les constructions synthétiques des nombres réels (voir l' axiome de la limite supérieure ), et il est également intimement lié à la construction des nombres réels à l'aide des coupes de Dedekind .

En théorie des ordres , cette propriété peut être généralisée à une notion de complétude pour tout ensemble partiellement ordonné . Un ensemble linéairement ordonné qui est dense et a la propriété de limite supérieure la moins élevée est appelé un continuum linéaire .

Déclaration de la propriété

Déclaration pour les nombres réels

Soit S un ensemble non vide de nombres réels .

• Un nombre réel x est appelé une limite supérieure pour S si x ≥ s pour tout s ∈ S .
• Un nombre réel x est la plus petite borne supérieure (ou supremum ) pour S si x est une borne supérieure pour S et x ≤ y pour chaque borne supérieure y de S .

La propriété de la limite supérieure la moins élevée indique que tout ensemble non vide de nombres réels qui a une limite supérieure doit avoir une limite supérieure minimale en nombres réels .

Généralisation aux ensembles ordonnés

Rouge : l'ensemble . Bleu : l'ensemble de ses bornes supérieures en .${\displaystyle \left\{x\in \mathbf {Q} :x^{2}\leq 2\right\}}$${\displaystyle \mathbf {Q} }$

Plus généralement, on peut définir une borne supérieure et une borne supérieure pour n'importe quel sous - ensemble d'un ensemble partiellement ordonné X , avec « nombre réel » remplacé par « élément de X ». Dans ce cas, nous disons que X a la propriété de borne supérieure la moins élevée si chaque sous-ensemble non vide de X avec une borne supérieure a une borne supérieure la moins élevée dans X .

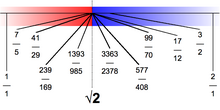
Par exemple, l'ensemble Q de nombres rationnels n'a pas la propriété de borne supérieure dans l'ordre habituel. Par exemple, l'ensemble

${\displaystyle \left\{x\in \mathbf {Q} :x^{2}\leq 2\right\}=\mathbf {Q} \cap \left(-{\sqrt {2}},{\ sqrt {2}}\right)}$

a une borne supérieure dans Q , mais n'a pas de borne supérieure dans Q (puisque la racine carrée de deux est irrationnelle ). La construction des nombres réels à l' aide des coupes de Dedekind profite de cet échec en définissant les nombres irrationnels comme les bornes supérieures de certains sous-ensembles des rationnels.

Preuve

Statut logique

La propriété de la borne supérieure est équivalente à d'autres formes de l' axiome de complétude , telles que la convergence des suites de Cauchy ou le théorème des intervalles emboîtés . Le statut logique de la propriété dépend de la construction des nombres réels utilisés : dans l' approche synthétique , la propriété est généralement prise comme axiome pour les nombres réels (voir axiome de la borne supérieure ) ; dans une approche constructive, la propriété doit être prouvée en tant que théorème , soit directement à partir de la construction, soit en conséquence d'une autre forme de complétude.

Preuve par suites de Cauchy

Il est possible de prouver la propriété de la borne supérieure en supposant que chaque séquence de Cauchy de nombres réels converge. Soit S un ensemble non vide de nombres réels. Si S a exactement un élément, alors son seul élément est une borne supérieure. Considérons donc S avec plus d'un élément et supposons que S a une borne supérieure B ₁ . Puisque S est non vide et a plus d'un élément, il existe un nombre réel A ₁ qui n'est pas une borne supérieure pour S . Définissez les séquences A ₁ , A ₂ , A ₃ , ... et B ₁ , B ₂ , B ₃ , ... de manière récursive comme suit :

1. Vérifiez si ( A _n + B _n ) 2 est une borne supérieure pour S .
2. Si c'est le cas, soit A _{n +1} = A _n et soit B _{n +1} = ( A _n + B _n ) 2 .
3. Sinon, il doit y avoir un élément s dans S pour que s >( A _n + B _n ) 2 . Soit A _{n +1} = s et soit B _{n +1} = B _n .

Ensuite , A ₁ ≤ A ₂ ≤ A ₃ ≤ ⋯ ≤ B ₃ ≤ B ₂ ≤ B ₁ et | A _n − B _n | → 0 comme n → ∞ . Il s'ensuit que les deux séquences sont de Cauchy et ont la même limite L , qui doit être la borne supérieure de S .

Applications

La propriété de limite supérieure de R peut être utilisée pour prouver plusieurs des principaux théorèmes fondamentaux de l'analyse réelle .

Théorème des valeurs intermédiaires

Soit f  : [ a , b ] → R une fonction continue , et supposons que f  ( a ) < 0 et f  ( b ) > 0 . Dans ce cas, le théorème des valeurs intermédiaires stipule que f doit avoir une racine dans l'intervalle [ a , b ] . Ce théorème peut être démontré en considérant l'ensemble

S  = { s [ a , b ] :  f  ( x ) < 0 pour tout x ≤ s } .

Autrement dit, S est le segment initial de [ a , b ] qui prend des valeurs négatives sous f . Alors b est une borne supérieure pour S , et la plus petite borne supérieure doit être une racine de f .

Théorème de Bolzano-Weierstrass

Le théorème de Bolzano-Weierstrass pour R stipule que chaque séquence x _n de nombres réels dans un intervalle fermé [ a , b ] doit avoir une sous- suite convergente . Ce théorème peut être démontré en considérant l'ensemble

S  = { s ∈ [ a , b ] :  s ≤ x _n pour une infinité de n }

Clairement, , et S n'est pas vide. De plus, b est une borne supérieure pour S , donc S a une borne supérieure c . Alors c doit être un point limite de la suite x _n , et il s'ensuit que x _n a une sous-suite qui converge vers c . ${\displaystyle a\in S}$

Théorème des valeurs extrêmes

Soit f  : [ a , b ] → R une fonction continue et soit M = sup f  ([ a , b ]) , où M = ∞ si f  ([ a , b ]) n'a pas de borne supérieure. Le théorème des valeurs extrêmes stipule que M est fini et f  ( c ) = M pour un certain c ∈ [ a , b ] . Ceci peut être prouvé en considérant l'ensemble

S  = { s ∈ [ a , b ] : sup f  ([ s , b ]) = M } .

Par définition de M , a ∈ S , et par sa propre définition, S est délimitée par b . Si c est la plus petite borne supérieure de S , alors il résulte de la continuité que f  ( c ) = M .

Théorème de Heine-Borel

Soit [ a , b ] un intervalle fermé dans R , et soit { U _α } une collection d' ouverts qui couvre [ a , b ] . Ensuite, le théorème de Heine-Borel énonce qu'une sous-collection finie de { U _α } couvre également [ a , b ] . Cette affirmation peut être prouvée en considérant l'ensemble

S  = { s ∈ [ a , b ]: [ a , s ] peut être couvert par un nombre fini U _α } .

L'ensemble S contient évidemment a , et est borné par b par construction. Par la propriété de la moindre borne supérieure , S a une borne supérieure c ∈ [ a , b ] . Par conséquent, c est lui - même un élément d'un ouvert U _α , et il en résulte pour c < b que [ a , c + δ ] peut être recouvert par un nombre fini U _α pour un certain suffisamment faible δ > 0 . Cela prouve que c + δ ∈ S et c n'est pas une borne supérieure pour S . Par conséquent, c = b .

Histoire

L'importance de la propriété la moins élevée a été reconnue pour la première fois par Bernard Bolzano dans son article de 1817 Rein analytischer Beweis des Lehrsatzes dass zwischen je zwey Werthen, die ein entgegengesetztes Resultat gewäahren, wenigstens eine reelle Wurzel der Gleichung liege .

Voir également

• Liste des sujets d'analyse réels

Remarques

Les références

• Abbott, Stephen (2001). Comprendre l'analyse . Textes de premier cycle en mathématiques. New York : Springer-Verlag. ISBN 0-387-95060-5.
• Aliprantis, Charalambos D ; Burkinshaw, Owen (1998). Principes de l'analyse réelle (troisième éd.). Académique. ISBN 0-12-050257-7.

• Bartle, Robert G.; Sherbert, Donald R. (2011). Introduction à l'analyse réelle (4 éd.). New York : John Wiley et fils. ISBN 978-0-471-43331-6.
• Bressoud, David (2007). Une approche radicale de l'analyse réelle . MAA. ISBN 978-0-88385-747-2.
• Browder, Andrew (1996). Analyse mathématique : une introduction . Textes de premier cycle en mathématiques . New York : Springer-Verlag. ISBN 0-387-94614-4.
• Dangello, Franck ; Seyfried, Michael (1999). Introduction à l'analyse réelle . Brooks Cole. ISBN 978-0-395-95933-6.
• Rudin, Walter (1976). Principes de l'analyse mathématique . Walter Rudin Student Series in Advanced Mathematics (3 ed.). McGraw–Hill. ISBN 978-0-07-054235-8.
• Willard, Stephen (2004) [1970]. Topologie générale . Mineola, NY : Publications de Douvres. ISBN 9780486434797.