Frustration géométrique - Geometrical frustration

En physique de la matière condensée , le terme frustration géométrique (ou en abrégé : frustration ) désigne un phénomène où les atomes ont tendance à se coller à des positions non triviales ou où, sur un réseau cristallin régulier , des forces inter-atomiques conflictuelles (chacune favorisant des , mais des structures différentes) conduisent à des structures assez complexes. En conséquence de la frustration dans la géométrie ou dans les forces, une plénitude d' états fondamentaux distincts peut résulter à température nulle, et l'ordre thermique habituel peut être supprimé à des températures plus élevées. Des exemples très étudiés sont les matériaux amorphes , les verres ou les aimants dilués .

Le terme frustration , dans le contexte des systèmes magnétiques , a été introduit par Gérard Toulouse (1977). En effet, les systèmes magnétiques frustrés avaient déjà été étudiés. Les premiers travaux comprend une étude du modèle d' Ising sur un réseau triangulaire avec le plus proche voisin spins couplé antiferromagnétique par, GH Wannier , publiée en 1950. Caractéristiques connexes se produire dans des aimants avec des interactions en compétition , où les deux ferromagnétique ainsi que des raccords antiferromagnétiques entre les paires de tours ou des moments magnétiques sont présents, le type d'interaction dépendant de la distance de séparation des spins. Dans ce cas, une commensurabilité , telle que des arrangements de spin hélicoïdal , peut en résulter, comme cela avait été discuté à l'origine, en particulier par A. Yoshimori, TA Kaplan, RJ Elliott et d'autres, à partir de 1959, pour décrire les découvertes expérimentales sur les métaux des terres rares. Un intérêt renouvelé pour de tels systèmes de spin avec des interactions frustrées ou concurrentes est apparu environ deux décennies plus tard, à partir des années 1970, dans le contexte des verres de spin et des superstructures magnétiques modulées spatialement. Dans les verres de spin, la frustration est augmentée par un désordre stochastique dans les interactions, comme cela peut se produire expérimentalement dans les alliages magnétiques non stoechiométriques . Les modèles de spin soigneusement analysés avec frustration incluent le modèle Sherrington-Kirkpatrick , décrivant les verres de spin, et le modèle ANNNI , décrivant les superstructures magnétiques de commensurabilité .

Commande magnétique

Figure 1 : Spins interagissant antiferromagnétiquement dans un arrangement triangulaire

Figure 2 : Spins interagissant antiferromagnétiquement dans un arrangement tétraédrique

Figure 3 : Spins le long des axes faciles d'un tétraèdre

Figure 4 : Spins faciles frustrés dans un tétraèdre

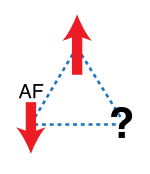
La frustration géométrique est une caractéristique importante du magnétisme , où elle découle de l'arrangement relatif des spins . Un exemple 2D simple est illustré à la figure 1. Trois ions magnétiques résident aux coins d'un triangle avec des interactions antiferromagnétiques entre eux ; l'énergie est minimisée lorsque chaque spin est aligné à l'opposé des voisins. Une fois que les deux premiers spins s'alignent de manière antiparallèle, le troisième est frustré car ses deux orientations possibles, haut et bas, donnent la même énergie. Le troisième spin ne peut pas simultanément minimiser ses interactions avec les deux autres. Puisque cet effet se produit pour chaque spin, l'état fondamental est sextuple dégénéré . Seuls les deux états où tous les spins sont en haut ou en bas ont plus d'énergie.

De même en trois dimensions, quatre spins disposés en tétraèdre (figure 2) peuvent connaître une frustration géométrique. S'il y a une interaction antiferromagnétique entre les spins, alors il n'est pas possible d'arranger les spins de sorte que toutes les interactions entre les spins soient antiparallèles. Il existe six interactions de plus proche voisin, dont quatre sont antiparallèles et donc favorables, mais dont deux (entre 1 et 2, et entre 3 et 4) sont défavorables. Il est impossible d'avoir toutes les interactions favorables et le système est frustré.

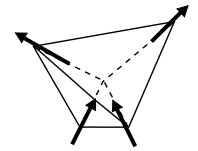
La frustration géométrique est également possible si les spins sont disposés de manière non colinéaire . Si nous considérons un tétraèdre avec un spin sur chaque sommet pointant le long de l' axe facile (c'est-à-dire directement vers ou loin du centre du tétraèdre), alors il est possible d'arranger les quatre spins de sorte qu'il n'y ait pas de spin net (Figure 3). C'est exactement équivalent à avoir une interaction antiferromagnétique entre chaque paire de spins, donc dans ce cas il n'y a pas de frustration géométrique. Avec ces axes, la frustration géométrique survient s'il y a une interaction ferromagnétique entre voisins, où l'énergie est minimisée par des spins parallèles. Le meilleur arrangement possible est illustré à la figure 4, avec deux tours pointant vers le centre et deux pointant vers l'extérieur. Le moment magnétique net pointe vers le haut, maximisant les interactions ferromagnétiques dans cette direction, mais les vecteurs gauche et droit s'annulent (c'est-à-dire sont alignés antiferromagnétiquement), comme le font vers l'avant et vers l'arrière. Il existe trois arrangements équivalents différents avec deux spins sortants et deux entrants, de sorte que l'état fondamental est triplement dégénéré.

Définition mathématique

La définition mathématique est simple (et analogue à la boucle dite de Wilson en chromodynamique quantique ) : On considère par exemple des expressions ("énergies totales" ou "Hamiltoniens") de la forme

${\displaystyle {\mathcal {H}}=\sum _{G}-I_{k_{\nu },k_{\mu }}\,\,S_{k_{\nu }}\cdot S_{k_{ \mu }}\,,}$

où G est le graphe considéré, tandis que les quantités I _{k ν , k μ} sont les énergies dites "d'échange" entre plus proches voisins, qui (dans les unités d'énergie considérées) prennent les valeurs ±1 (mathématiquement, c'est un signe graph ), tandis que les S _{k ν} · S _{k μ} sont des produits internes de spins scalaires ou vectoriels ou de pseudo-spins. Si le graphe G a des faces quadratiques ou triangulaires P , apparaissent les " variables plaquettes " P _W , " produits-boucles " du genre suivant :

${\style d'affichage P_{W}=I_{1,2}\,I_{2,3}\,I_{3,4}\,I_{4,1}}$et respectivement,${\displaystyle P_{W}=I_{1,2}\,I_{2,3}\,I_{3,1}\,,}$

qui sont aussi appelés « produits de frustration ». Il faut faire une somme sur ces produits, sommer sur toutes les plaquettes. Le résultat pour une seule plaquette est +1 ou -1. Dans le dernier cas mentionné, la plaquette est "géométriquement frustrée".

On peut montrer que le résultat a une simple invariance de jauge : elle ne change pas – pas plus que d'autres grandeurs mesurables, par exemple « l'énergie totale » – même si localement les intégrales d'échange et les spins sont modifiés simultanément comme suit : ${\displaystyle {\mathcal {H}}}$

${\displaystyle I_{i,k}\to \varepsilon _{i}I_{i,k}\varepsilon _{k},\quad S_{i}\to \varepsilon _{i}S_{i},\ quad S_{k}\à \varepsilon _{k}S_{k}\,.}$

Ici , les nombres e _i et ε _k sont des signes arbitraires, soit +1 ou -1, de sorte que la structure modifiée peut sembler totalement aléatoire.

Eau glacée

Figure 5 : Schéma des molécules de glace d'eau

Bien que la plupart des recherches précédentes et actuelles sur la frustration se concentrent sur les systèmes de spin, le phénomène a d'abord été étudié dans la glace ordinaire . En 1936, Giauque et Stout publient L'entropie de l'eau et la troisième loi de la thermodynamique. Capacité calorifique de la glace de 15 K à 273 K , rapportant des mesures calorimétriques sur l'eau à travers les transitions de congélation et de vaporisation jusqu'à la phase gazeuse à haute température. L' entropie a été calculée en intégrant la capacité calorifique et en ajoutant les apports de chaleur latente ; les mesures à basse température ont été extrapolées à zéro, en utilisant la formule de Debye alors récemment dérivée. L'entropie résultante, S ₁  = 44,28 cal/(K·mol) = 185,3 J/(mol·K) a été comparée au résultat théorique de la mécanique statistique d'un gaz  parfait , S ₂ = 45,10 cal/(K·mol) = 188,7 J/(mol·K). Les deux valeurs diffèrent de S ₀  = 0,82 ± 0,05 cal/(K·mol) = 3,4 J/(mol·K). Ce résultat a ensuite été expliqué par Linus Pauling avec une excellente approximation, qui a montré que la glace possède une entropie finie (estimée à 0,81 cal/(K·mol) ou 3,4 J/(mol·K)) à température nulle en raison du désordre configurationnel intrinsèque aux protons de la glace.

Dans le hexagonal ou cubique phase de glace l' oxygène des ions forment une structure tétraédrique avec une longueur de la liaison O-O 2,76  Å (276  pm ), tandis que les mesures de longueur de la liaison O-H seulement 0,96 Å (96 pm). Chaque ion oxygène (blanc) est entouré de quatre ions hydrogène (noir) et chaque ion hydrogène est entouré de 2 ions oxygène, comme le montre la figure 5. En maintenant la structure interne de la molécule H ₂ O, la position d'énergie minimale d'un proton n'est pas à mi-chemin entre deux ions oxygène adjacents. Il y a deux positions équivalentes qu'un hydrogène peut occuper sur la ligne de la liaison O–O, une position éloignée et une position proche. Ainsi une règle conduit à la frustration des positions du proton pour une configuration d'état fondamental : pour chaque oxygène deux des protons voisins doivent résider dans la position éloignée et deux d'entre eux dans la position proche, ce qu'on appelle les « règles de glace ». Pauling a proposé que la structure tétraédrique ouverte de la glace offre de nombreux états équivalents satisfaisant les règles de la glace.

Pauling a ensuite calculé l'entropie configurationnelle de la manière suivante : considérons une mole de glace, constituée de N O ²⁻ et de 2 N protons. Chaque liaison O–O a deux positions pour un proton, conduisant à 2 ^{2 N} configurations possibles. Cependant, parmi les 16 configurations possibles associées à chaque oxygène, seules 6 sont énergétiquement favorables, maintenant la contrainte de la molécule H ₂ O. Ensuite, une limite supérieure des nombres que l'état fondamental peut prendre est estimée comme Ω  < 2 ^{2 N} (6/16) ^N . En conséquence, l'entropie configurationnelle S ₀  = k _B ln( Ω ) = Nk _B ln(3/2) = 0,81 cal/(K·mol) = 3,4 J/(mol·K) est en accord étonnant avec l'entropie manquante mesurée par Giauque et Stout.

Bien que le calcul de Pauling ait négligé à la fois la contrainte globale sur le nombre de protons et la contrainte locale résultant des boucles fermées sur le réseau de Wurtzite, l'estimation s'est par la suite avérée d'une excellente précision.

Faire tourner la glace

Figure 6 : Schéma des molécules de glace de spin

Une situation mathématiquement analogue à la dégénérescence de la glace d'eau se trouve dans les glaces de spin . Une structure de glace de spin commune est illustrée à la figure 6 dans la structure de pyrochlore cubique avec un atome ou un ion magnétique résidant à chacun des quatre coins. En raison du fort champ cristallin dans le matériau, chacun des ions magnétiques peut être représenté par un doublet d'état fondamental d'Ising avec un moment important. Cela suggère une image de spins d'Ising résidant sur le réseau tétraédrique partageant les coins avec des spins fixés le long de l'axe de quantification local, les axes cubiques <111> , qui coïncident avec les lignes reliant chaque sommet tétraédrique au centre. Chaque cellule tétraédrique doit avoir deux spins pointant vers l'intérieur et deux pointant vers l'extérieur afin de minimiser l'énergie. Actuellement, le modèle de glace de spin a été approximativement réalisé par des matériaux réels, notamment les pyrochlores de terres rares Ho ₂ Ti ₂ O ₇ , Dy ₂ Ti ₂ O ₇ et Ho ₂ Sn ₂ O ₇ . Ces matériaux présentent tous une entropie résiduelle non nulle à basse température.

Extension du modèle de Pauling : frustration générale

Le modèle de glace de spin n'est qu'une subdivision des systèmes frustrés. Le mot frustration a été initialement introduit pour décrire l'incapacité d'un système à minimiser simultanément l'énergie d'interaction concurrente entre ses composants. En général, la frustration est causée soit par des interactions concurrentes dues au désordre du site (voir aussi le modèle de Villain ) ou par une structure en réseau telle que dans les réseaux triangulaire , cubique à faces centrées (fcc), hexagonal compact , tétraèdre , pyrochlore et kagome avec interaction antiferromagnétique. La frustration se divise donc en deux catégories : la première correspond au verre de spin , qui présente à la fois un désordre dans la structure et une frustration dans le spin ; la seconde est la frustration géométrique avec une structure en treillis ordonnée et la frustration de spin. La frustration d'un verre de spin est comprise dans le cadre du modèle RKKY , dans lequel la propriété d'interaction, ferromagnétique ou antiferromagnétique, dépend de la distance des deux ions magnétiques. En raison du désordre du réseau dans le verre de spin, un spin d'intérêt et ses voisins les plus proches pourraient être à des distances différentes et avoir une propriété d'interaction différente, ce qui conduit ainsi à un alignement préféré différent du spin.

Ferromagnétiques artificiels géométriquement frustrés

À l'aide de techniques de lithographie, il est possible de fabriquer des îlots magnétiques de taille inférieure au micromètre dont la disposition géométrique reproduit la frustration que l'on trouve dans les matériaux de glace de spin naturels. Récemment RF Wang et al. ont rapporté la découverte d'un aimant artificiel géométriquement frustré composé de réseaux d'îlots ferromagnétiques à domaine unique fabriqués par lithographie. Ces îles sont disposées manuellement pour créer un analogue bidimensionnel pour faire tourner la glace. Les moments magnétiques des îlots de « spin » ordonnés ont été imagés par microscopie à force magnétique (MFM) , puis l'accommodation locale de la frustration a été soigneusement étudiée. Dans leurs travaux antérieurs sur un réseau carré d'aimants frustrés, ils ont observé à la fois des corrélations à courte portée de type glace et l'absence de corrélations à longue portée, tout comme dans la glace de spin à basse température. Ces résultats renforcent le terrain inexploré sur lequel la physique réelle de la frustration peut être visualisée et modélisée par ces aimants artificiels géométriquement frustrés, et inspirent de nouvelles activités de recherche.

Ces ferroaimants artificiellement frustrés peuvent présenter des propriétés magnétiques uniques lors de l'étude de leur réponse globale à un champ externe à l'aide de l'effet Kerr magnéto-optique. En particulier, une dépendance angulaire non monotone de la coercivité du réseau carré est liée au désordre dans le système de glace de spin artificielle.

Frustration géométrique sans treillis

Un autre type de frustration géométrique provient de la propagation d'un ordre local. Une question principale à laquelle un physicien de la matière condensée est confronté est d'expliquer la stabilité d'un solide.

Il est parfois possible d'établir des règles locales, de nature chimique, qui conduisent à des configurations à basse énergie et régissent donc l'ordre structural et chimique. Ce n'est généralement pas le cas et souvent l'ordre local défini par les interactions locales ne peut pas se propager librement, ce qui conduit à une frustration géométrique. Une caractéristique commune à tous ces systèmes est que, même avec des règles locales simples, ils présentent un large ensemble de réalisations structurelles, souvent complexes. La frustration géométrique joue un rôle dans les domaines de la matière condensée, allant des amas et des solides amorphes aux fluides complexes.

La méthode générale d'approche pour résoudre ces complications suit deux étapes. Premièrement, la contrainte de remplissage parfait de l'espace est assouplie en tenant compte de la courbure de l'espace. Une structure idéale, sans frustration, est définie dans cet espace courbe. Ensuite, des distorsions spécifiques sont appliquées à ce modèle idéal afin de l'intégrer dans l'espace euclidien en trois dimensions. La structure finale est un mélange de régions ordonnées, où l'ordre local est similaire à celui du gabarit, et de défauts résultant de l'encastrement. Parmi les défauts possibles, les désorientations jouent un rôle important.

Le pavage d'un plan par des pentagones est impossible mais peut être réalisé sur une sphère en forme de dodécaèdre pentagonal comme démontré dans les quasicristaux

Exemples simples en deux dimensions

Des exemples bidimensionnels sont utiles pour comprendre l'origine de la compétition entre les règles locales et la géométrie dans le grand. Considérons d'abord un arrangement de disques identiques (un modèle pour un métal bidimensionnel hypothétique) sur un plan ; on suppose que l'interaction entre disques est isotrope et tend localement à disposer les disques de la manière la plus dense possible. Le meilleur arrangement pour trois disques est trivialement un triangle équilatéral avec les centres des disques situés aux sommets du triangle. L'étude de la structure à longue portée peut donc être réduite à celle de pavages plans à triangles équilatéraux. Une solution bien connue est apportée par le pavage triangulaire avec une compatibilité totale entre les règles locales et globales : le système est dit « non frustré ».

Mais maintenant, l'énergie d'interaction est censée être au minimum lorsque les atomes sont assis sur les sommets d'un pentagone régulier . Essayer de propager à longue distance un tassement de ces pentagones partageant des arêtes (liaisons atomiques) et des sommets (atomes) est impossible. Cela est dû à l'impossibilité de carreler un plan avec des pentagones réguliers, simplement parce que l'angle au sommet pentagone ne divise pas 2 π . Trois de ces pentagones peuvent facilement s'adapter à un sommet commun, mais un espace reste entre deux arêtes. C'est ce genre de décalage que l'on appelle « frustration géométrique ». Il existe un moyen de surmonter cette difficulté. Soit la surface à carreler exempte de toute topologie présupposée, et construisons le pavage avec une application stricte de la règle d'interaction locale. Dans cet exemple simple, nous observons que la surface hérite de la topologie d'une sphère et reçoit ainsi une courbure. La structure finale, ici un dodécaèdre pentagonal, permet une parfaite propagation de l'ordre pentagonal. C'est ce qu'on appelle un modèle « idéal » (sans défaut) pour la structure considérée.

Structures denses et garnissages tétraédriques

Emballage tétraédrique: L' angle dièdre d'un tétraèdre est pas commensurable avec 2 π ; par conséquent, un trou subsiste entre deux faces d'un garnissage de cinq tétraèdres avec une arête commune. Un emballage de vingt tétraèdres avec un sommet commun de telle sorte que les douze sommets externes forment un icosaèdre irrégulier

La stabilité des métaux est une question de longue date de la physique du solide, qui ne peut être comprise dans le cadre de la mécanique quantique qu'en prenant correctement en compte l'interaction entre les ions chargés positivement et les électrons de valence et de conduction. Il est néanmoins possible d'utiliser une image très simplifiée de la liaison métallique et de ne conserver qu'un type d'interactions isotropes, conduisant à des structures qui peuvent être représentées comme des sphères densément emballées. Et en effet, les structures métalliques simples cristallines sont souvent soit des réseaux cubiques à faces centrées (fcc) ou hexagonaux (hcp). Dans une certaine mesure, les métaux amorphes et les quasicristaux peuvent également être modélisés par empilement serré de sphères. L'ordre atomique local est bien modélisé par un tassement serré de tétraèdres, conduisant à un ordre icosaédrique imparfait.

Un tétraèdre régulier est la configuration la plus dense pour l'emballage de quatre sphères égales. Le problème de compactage aléatoire dense de sphères dures peut ainsi être appliqué au problème de compactage tétraédrique . C'est un exercice pratique que d'essayer d'emballer des balles de tennis de table afin de ne former que des configurations tétraédriques. On part de quatre boules disposées en tétraèdre parfait, et on essaie d'ajouter de nouvelles sphères, tout en formant de nouveaux tétraèdres. La solution suivante, avec cinq boules, est trivialement deux tétraèdres partageant une face commune ; notez que déjà avec cette solution, la structure fcc, qui contient des trous tétraédriques individuels, ne montre pas une telle configuration (les tétraèdres partagent des arêtes, pas des faces). Avec six boules, trois tétraèdres réguliers sont construits, et l'amas est incompatible avec toutes les structures cristallines compactes (fcc et hcp). L'ajout d'une septième sphère donne un nouvel amas constitué de deux boules "axiales" se touchant et cinq autres touchant ces deux dernières boules, la forme extérieure étant une bipyramide pentagonale presque régulière. Cependant, nous sommes maintenant confrontés à un véritable problème d'emballage, analogue à celui rencontré ci-dessus avec le pavage pentagonal en deux dimensions. L'angle dièdre d'un tétraèdre est pas commensurable avec 2 π ; par conséquent, un trou subsiste entre deux faces de tétraèdres voisins. En conséquence, un pavage parfait de l'espace euclidien R ³ est impossible avec des tétraèdres réguliers. La frustration a un caractère topologique : il est impossible de remplir l'espace euclidien de tétraèdres, même fortement déformés, si l'on impose qu'un nombre constant de tétraèdres (ici cinq) partagent une arête commune.

La prochaine étape est cruciale : la recherche d'une structure non frustrée en tenant compte de la courbure dans l'espace , afin que les configurations locales se propagent à l'identique et sans défauts dans tout l'espace.

Emballage régulier de tétraèdres : le polytope {3,3,5}

600-cellule : polytope {3,3,5}

Pack de vingt tétraèdres irréguliers avec un sommet commun de telle sorte que les douze sommets externes forment un icosaèdre régulier. En effet, la longueur du bord de l'icosaèdre l est légèrement plus longue que le rayon de la circonsphère r ( l  ≈ 1,05 r ). Il existe une solution avec des tétraèdres réguliers si l'espace n'est pas euclidien, mais sphérique. Il s'agit du polytope {3,3,5}, utilisant la notation de Schläfli , également connu sous le nom de 600-cell .

Il y a cent vingt sommets qui appartiennent tous à l'hypersphère S ³ de rayon égal au nombre d' or ( φ  = 1 + √ 5/2) si les arêtes sont de longueur unitaire. Les six cents cellules sont des tétraèdres réguliers regroupés par cinq autour d'un bord commun et par vingt autour d'un sommet commun. Cette structure est appelée un polytope (voir Coxeter ) qui est le nom général en dimension supérieure dans la série contenant des polygones et des polyèdres. Même si cette structure est intégrée à quatre dimensions, elle a été considérée comme une variété tridimensionnelle (courbe). Ce point est conceptuellement important pour la raison suivante. Les modèles idéaux qui ont été introduits dans l'espace incurvé sont des modèles incurvés en trois dimensions. Ils ressemblent localement à des modèles euclidiens tridimensionnels. Ainsi, le polytope {3,3,5}, qui est un pavage par tétraèdres, fournit une structure atomique très dense si des atomes sont localisés sur ses sommets. Il sert donc naturellement de gabarit aux métaux amorphes, mais il ne faut pas oublier qu'il se fait au prix d'idéalisations successives.

Littérature

• Sadoc, JF ; Mosseri, R. (2007). Frustration géométrique (éd. réédité). La presse de l'Universite de Cambridge. ISBN 9780521031875.
• Sadoc, JF, éd. (1990). Géométrie en physique de la matière condensée . Singapour : World Scientific. ISBN 9789810200893.
• Coxeter, HSM (1973). Polytopes réguliers . Éditions Douvres. ISBN 9780486614809.

Les références