600 cellules - 600-cell

600 cellules
Diagramme de Schlegel , centré sur les sommets (sommets et arêtes)
Taper	Convexe régulier 4-polytope
Symbole Schläfli	{3,3,5}
Diagramme de Coxeter
Cellules	600 ( 3.3.3 )
Visages	1200 {3}
Bords	720
Sommets	120
Figure de sommet	icosaèdre
Polygone de Pétrie	30-gon
Groupe Coxeter	H 4 , [3,3,5], ordre 14400
Double	120 cellules
Propriétés	convexe , isogonal , isotoxal , isoedrique
Indice uniforme	35

Rapporter

En géométrie , la cellule 600 est le 4-polytope régulier convexe (analogue à quatre dimensions d'un solide platonicien ) avec le symbole de Schläfli {3,3,5}. Il est également connu sous le nom de C ₆₀₀ , hexacosichoron et hexacosièdre . On l'appelle aussi un tétraplexe (en abrégé de "complexe tétraédrique") et un polytétraèdre , étant délimité par des cellules tétraédriques .

La limite des 600 cellules est composée de 600 cellules tétraédriques dont 20 se rencontrent à chaque sommet. Ensemble, ils forment 1200 faces triangulaires, 720 arêtes et 120 sommets. C'est l' analogue à 4 dimensions de l' icosaèdre , car il a cinq tétraèdres se rencontrant à chaque arête, tout comme l'icosaèdre a cinq triangles se rencontrant à chaque sommet. Son double polytope est le 120-cell .

Géométrie

Le 600-cellule est le cinquième dans la séquence de 6 4-polytopes réguliers convexes (par ordre de taille et de complexité). Il peut être déconstruit en vingt-cinq instances qui se chevauchent de son prédécesseur immédiat le 24 cellules , comme le 24 cellules peut être déconstruit en trois instances qui se chevauchent de son prédécesseur le tesseract (8-cell) , et le 8-cell peut être déconstruit en deux instances qui se chevauchent de son prédécesseur le 16-cell .

La procédure inverse pour construire chacun de ceux-ci à partir d'une instance de son prédécesseur préserve le rayon du prédécesseur, mais produit généralement un successeur avec une longueur d'arête plus petite. La longueur du bord des 24 cellules est égale à son rayon, mais la longueur du bord des 600 cellules est d'environ 0,618 fois son rayon. Le rayon et la longueur des bords des 600 cellules sont dans le nombre d' or .

4-polytopes convexes réguliers
Groupe Symétrie	Un 4	B 4		F 4	H 4
Nom	5 cellules hyper- tétraèdre	16 cellules Hyper- octaèdre	8 cellules Hyper- cube	24 cellules	600 cellules Hyper- icosaèdre	120 cellules Hyper- dodécaèdre
Symbole Schläfli	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Diagramme de Coxeter
Graphique
Sommets	5	8	16	24	120	600
Bords	dix	24	32	96	720	1200
Visages	10 triangles	32 triangles	24 carrés	96 triangles	1200 triangles	720 pentagones
Cellules	5 tétraèdres	16 tétraèdres	8 cubes	24 octaèdres	600 tétraèdres	120 dodécaèdres
Rayon long	1	1	1	1	1	1
Longueur du bord	√ 5/√ 2 1.581	√ 2 ≈ 1,414	1	1	1/?? 0,618	1/√ 2 φ 2 0,270
Rayon court	1/4	1/2	1/2	√ 2/2 0,707	1 - (√ 2/2 √ 3 φ) 2 0,936	1 - (1/2 √ 3 φ) 2 0,968
Zone	dix•√ 8/3 9.428	32•√ 3/4 13.856	24	96•√ 3/4 41.569	1200•√ 3/8φ 2 99.238	720•25 + 10 √ 5/8φ 4 621,9
Le volume	5•5 √ 5/24 2.329	16•1/3 5.333	8	24•√ 2/3 11.314	600•1/3 √ 8 φ 3 16.693	120•2 + φ/2 √ 8 φ 3 18.118
4-Contenu	√ 5/24•(√ 5/2) 4 0,146	2/3 0,667	1	2	Court∙Vol/4 3.907	Court∙Vol/4 4.385

Coordonnées

Rayon unitaire Coordonnées cartésiennes

Les sommets d'une cellule de 600 cellules de rayon unitaire centrées à l'origine de l'espace 4, avec des arêtes de longueur 1/?? ≈ 0,618 (où φ = 1 + √ 5/2≈ 1,618 est le nombre d' or ), peut être donné comme suit :

8 sommets obtenus à partir de

(0, 0, 0, ±1)

en permutant les coordonnées, et 16 sommets de la forme :

(±1/2, ±1/2, ±1/2, ±1/2)

Les 96 sommets restants sont obtenus en prenant des permutations paires de

(±??/2, ±1/2, ±φ ^-1/2, 0)

Notez que les 8 premiers sont les sommets d'un 16-cell , les 16 seconds sont les sommets d'un tesseract , et ces 24 sommets ensemble sont les sommets d'un 24-cell . Les 96 sommets restants sont les sommets d'un snub 24-cell , qui peut être trouvé en partitionnant chacun des 96 bords d'un autre 24-cell (double à la première) dans le nombre d'or de manière cohérente.

Lorsqu'ils sont interprétés comme des quaternions , ce sont les unités icosiennes .

Dans les 24 cellules, il y a des carrés , des hexagones et des triangles qui reposent sur de grands cercles (dans des plans centraux passant par quatre ou six sommets). Dans les 600 cellules, il y a vingt-cinq cellules inscrites qui se chevauchent, chaque carré étant unique à une cellule de 24, chaque hexagone ou triangle partagé par deux cellules de 24 et chaque sommet partagé entre cinq cellules de 24.

Coordonnées sphériques de Hopf

Dans la cellule 600, il y a aussi des pentagones et décagones de grands cercles (dans les plans centraux passant par dix sommets).

Seuls les bords du décagone sont des éléments visibles du 600-cell (car ce sont les bords du 600-cell). Les bords des autres polygones de grand cercle sont des accords intérieurs de 600 cellules, qui ne sont montrés dans aucun des rendus de 600 cellules de cet article.

Par symétrie, un nombre égal de polygones de chaque sorte passent par chaque sommet ; il est donc possible de prendre en compte les 120 sommets comme l'intersection d'un ensemble de polygones centraux d'une seule sorte : décagones, hexagones, pentagones, carrés ou triangles. Par exemple, les 120 sommets peuvent être considérés comme les sommets de 15 paires de carrés complètement orthogonaux qui ne partagent aucun sommet, ou comme 100 paires doubles d'hexagones non orthogonaux entre lesquels toutes les paires d'axes sont orthogonales, ou comme 144 non orthogonales pentagones dont six se coupent à chaque sommet. Cette dernière symétrie pentagonale de la cellule 600 est capturée par l'ensemble des coordonnées de Hopf (𝜉 _i , 𝜂, 𝜉 _j ) donné par :

({<10}??/5, {≤5}??/dix, {<10}??/5)

où {<10} est la permutation des dix chiffres (0 1 2 3 4 5 6 7 8 9) et {≤5} est la permutation des six chiffres (0 1 2 3 4 5). Les coordonnées 𝜉 _i et 𝜉 _j s'étendent sur les 10 sommets des décagones des grands cercles ; les chiffres pairs et impairs désignent les sommets des deux grands pentagones circulaires inscrits dans chaque décagone.

Structure

Sections polyédriques

Les distances mutuelles des sommets, mesurées en degrés d'arc sur l' hypersphère circonscrite , n'ont pour valeurs que 36° =??/5, 60° = ??/3, 72° = 2𝜋/5, 90° = ??/2, 108° = 3𝜋/5, 120° = 2𝜋/3, 144° = 4𝜋/5, et 180° = . Partant d'un sommet arbitraire V on a à 36° et 144° les 12 sommets d'un icosaèdre , à 60° et 120° les 20 sommets d'un dodécaèdre , à 72° et 108° les 12 sommets d'un plus grand icosaèdre, à 90 ° les 30 sommets d'un icosidodécaèdre , et enfin à 180° le sommet antipodal de V. Ceux-ci peuvent être vus dans les projections planes de Coxeter H3 avec des sommets superposés colorés.

Ces sections polyédriques sont des solides dans le sens où elles sont tridimensionnelles, mais bien sûr tous leurs sommets se trouvent à la surface de la cellule 600 (ils sont creux, pas pleins). Chaque polyèdre se trouve dans l'espace euclidien à 4 dimensions sous la forme d'une section transversale parallèle à travers les 600 cellules (un hyperplan). Dans l'espace tridimensionnel incurvé de l'enveloppe limite des 600 cellules, le polyèdre entoure le sommet V de la même manière qu'il entoure son propre centre. Mais son propre centre se trouve à l'intérieur de la cellule 600, pas à sa surface. V n'est pas réellement au centre du polyèdre, car il est déplacé vers l'extérieur de cet hyperplan dans la quatrième dimension, à la surface de la cellule 600. Ainsi V est le sommet d'une 4-pyramide basée sur le polyèdre.

Coques concentriques
	La cellule 600 est projetée en 3D en utilisant une base orthonormée. Les sommets sont triés et comptés selon leur norme 3D. La génération de l'enveloppe de plus en plus transparente de chaque ensemble de normes comptées montre : 1) deux points à l'origine 2) deux icosaèdres 3) deux dodécaèdres 4) deux plus grands icosaèdres 5) et un seul icosidodécaèdre pour un total de 120 sommets.

Accords de sommet

Géométrie de sommet de la cellule 600, montrant les 5 polygones de grand cercle réguliers et les 8 longueurs de corde de sommet à sommet avec des angles d'arc. Le nombre d'or régit les racines fractionnaires de tous les autres accords et les triangles d'or radiaux qui se rencontrent au centre.

Les 120 sommets sont répartis à huit longueurs de cordes différentes les unes des autres. Ces arêtes et cordes de la cellule 600 sont simplement les arêtes et cordes de ses cinq polygones de grand cercle. Dans l' ordre croissant de longueur, ils sont √ 0.Δ , √ 1 , √ 1.Δ , √ 2 , √ 2.Φ , √ 3 , √ 3.Φ et √ 4 .

Notez que les quatre accords hypercubiques des 24 cellules ( √ 1 , √ 2 , √ 3 , √ 4 ) alternent avec les quatre nouveaux accords des grands cercles supplémentaires des 600 cellules, les décagones et les pentagones. Les nouvelles longueurs de corde sont nécessairement racines carrées des fractions, mais fractions très spéciales concernant le nombre d' or , y compris les deux sections d' or de √ 5 , comme représenté sur le schéma.

Enveloppes frontières

Une projection 3D d'une cellule de 600 effectuant une simple rotation . La surface 3D composée de 600 tétraèdres est visible.

Les 600 cellules complètent les 24 cellules en ajoutant 96 sommets supplémentaires entre les 24 sommets existants des 24 cellules, ajoutant en fait 24 autres cellules superposées inscrites dans les 600 cellules. La nouvelle surface ainsi formée est un pavage de cellules et de faces plus petites et plus nombreuses : tétraèdres de longueur d'arête1/??≈ 0,618 à la place d'octaèdres de longueur de bord 1. Il renferme les √ 1 bords des cellules 24, qui deviennent invisibles cordes intérieures de la cellule 600, comme le √ 2 et √ 3 accords .

Une projection 3D d'une cellule de 24 effectuant une simple rotation . La surface 3D composée de 24 octaèdres est visible. Il est également présent dans la cellule 600, mais comme une enveloppe frontière intérieure invisible.

Comme les tétraèdres sont constitués d'arêtes triangulaires plus courtes que les octaèdres (d'un facteur de 1/??, le nombre d'or inverse), la cellule 600 n'a pas de longueur d'arête unitaire dans un système de coordonnées de rayon unitaire comme le font la cellule 24 et le tesseract ; contrairement à ces deux-là, la cellule 600 n'est pas radialement équilatérale . Comme eux, il est radialement triangulaire d'une manière particulière, mais dans laquelle des triangles d'or plutôt que des triangles équilatéraux se rencontrent au centre.

L'enveloppe limite de 600 petites cellules tétraédriques s'enroule autour des vingt-cinq enveloppes de 24 cellules octaédriques (en ajoutant un espace à 4 dimensions par endroits entre ces enveloppes à 3 dimensions). La forme de ces interstices doit être une sorte de pyramide octaédrique 4 , mais dans les 600 cellules, elle n'est pas régulière .

Géodésiques

Les cordes des sommets des 600 cellules sont disposées en polygones de grand cercle géodésiques de cinq sortes : décagones, hexagones, pentagones, carrés et triangles.

Projection stéréographique centrée sur les cellules des 72 décagones centraux des 600 cellules sur leurs grands cercles. Chaque grand cercle est divisé en 10 arcs-arêtes aux intersections où 6 grands cercles se croisent.

Les arêtes √ 0.𝚫 = forment 72 décagones centraux plats et réguliers , dont 6 se croisent à chaque sommet. Tout comme l' icosidodécaèdre peut être partitionné en 6 décagones centraux (60 arêtes = 6 × 10), la cellule 600 peut être partitionnée en 72 décagones (720 arêtes = 72 × 10). Les 720 √ 0.Δ bords divisent la surface en 1200 faces triangulaires et 600 cellules tétraédriques: a 600 cellules. Les 720 arêtes se présentent en 360 paires parallèles, distantes de √ 3.𝚽 . Comme dans le décagone et l'icosidodécaèdre, les bords se présentent en triangles d'or qui se rejoignent au centre du polytope. Les 72 grands décagones peuvent être divisés en 6 ensembles de 12 géodésiques parallèles Clifford sans intersection , de sorte qu'un seul grand cercle décagonal de chaque ensemble passe par chaque sommet, et les 12 décagones de chaque ensemble atteignent les 120 sommets.

Les √ 1 membrures forment 200 hexagones centraux (25 séries de 16, avec chaque hexagone en deux sets), 10 qui se croisent au niveau de chaque sommet (4 à partir de chacun des cinq cellules 24, chaque hexagone dans deux des cellules 24) . Chaque ensemble de 16 hexagones se compose des 96 arêtes et 24 sommets de l'une des 25 24 cellules inscrites qui se chevauchent. Les cordes √ 1 joignent des sommets distants de deux arêtes √ 0.𝚫 . Chaque corde √ 1 est le long diamètre d'une paire de cellules tétraédriques liées par la face (une bipyramide triangulaire ) et passe par le centre de la face partagée. Comme il y a 1200 faces, il y a 1200 √ 1 accords, en 600 paires parallèles, √ 3 d' intervalle. Les plans hexagonaux ne sont pas orthogonaux (60 degrés l'un de l'autre) mais ils se présentent sous forme de 100 paires doubles dans lesquelles les 3 axes d'un hexagone sont orthogonaux aux 3 axes de son double. Les 200 grands hexagones peuvent être divisés en 10 ensembles de 20 géodésiques parallèles Clifford sans intersection, de sorte qu'un seul grand cercle hexagonal de chaque ensemble passe par chaque sommet et que les 20 hexagones de chaque ensemble atteignent les 120 sommets.

Les √ 1.Δ accords forment 144 pentagones centraux, dont 6 se croisent à chaque sommet. Les √ 1.Δ que les 72 accords décagones exécuter sommet à chaque sommet-seconde dans les mêmes plans: deux pentagones sont inscrites dans chaque décagone. Les cordes √ 1.𝚫 joignent des sommets distants de deux arêtes √ 0.𝚫 sur un grand cercle géodésique. Les 720 √ 1.Δ accords se produisent dans 360 paires parallèles, √ 2.Φ = & phiv d' intervalle.

Les √ 2 cordes forment 450 carrés centraux (25 ensembles disjoints de 18), 15 qui se croisent au niveau de chaque sommet (3 à partir de chacune des cinq cellules 24). Chaque ensemble de 18 carrés se compose des 72 √ 2 arêtes et 24 sommets de l' un des 25 cellules de chevauchement inscrit 24. Les cordes √ 2 joignent des sommets distants de trois arêtes √ 0.𝚫 (et de deux cordes √ 1 ). Chaque corde √ 2 est le long diamètre d'une cellule octaédrique dans une seule cellule de 24. Il y a 1800 √ 2 accords, en 900 paires parallèles, √ 2 à part. Les 450 grands carrés (225 paires complètement orthogonales) peuvent être divisés en 15 ensembles de 30 géodésiques parallèles Clifford sans intersection, de sorte qu'un seul grand cercle carré de chaque ensemble passe par chaque sommet, et les 30 carrés de chaque ensemble atteignent les 120 sommets.

Les accords √ 2.𝚽 = φ forment les jambes de 720 triangles isocèles centraux (72 séries de 10 inscrits dans chaque décagone), dont 6 se croisent à chaque sommet. La troisième arête (base) de chaque triangle isocèle est de longueur √ 3.𝚽 . Les √ 2.Φ cordes entrent sommet à chaque sommet-tiers dans les mêmes plans que les 72 décagones, joignant les sommets qui sont trois √ 0.Δ bords d' intervalle sur un grand cercle géodésique. Il y a 720 accords distincts √ 2.𝚽 , en 360 paires parallèles, espacés de √ 1.𝚫 .

Les √ 3 cordes forment 400 triangles centraux équilatéraux (25 séries de 32, avec chaque triangle en deux sets), 10 qui se croisent au niveau de chaque sommet (4 à partir de chacune des cinq cellules 24 , chaque triangle dans deux des cellules 24 ). Chaque ensemble de 32 triangles se compose des 96 √ 3 accords et des 24 sommets de l'une des 25 cellules inscrites superposées. Les √ 3 cordes entrent sommet à chaque sommet-seconde dans les mêmes plans que les 200 hexagones: deux triangles sont inscrites dans chaque hexagone. Les √ 3 accords rejoignent les sommets qui sont quatre √ 0.Δ arêtes à part (et deux √ 1 accords à part sur un grand cercle géodésique). Chaque corde √ 3 est le diamètre long de deux cellules cubiques dans les mêmes 24 cellules. Il y a 1200 √ 3 accords, en 600 paires parallèles, √ une de l' autre.

Les √ 3.Φ accords (les diagonales des pentagones) forment les branches de 720 triangles isocèles centraux (144 ensembles de 5 inscrits dans chaque pentagone), dont 6 se croisent à chaque sommet. La troisième arête (base) de chaque triangle isocèle est une arête du pentagone de longueur √ 1.𝚫 , ce sont donc des triangles d'or. Les √ 3.Φ accords courent sommet à chaque quart-sommet dans les mêmes plans que les 72 décagones, joignant les sommets qui sont quatre √ 0.Δ arêtes à part sur un grand cercle géodésique. Il existe 720 accords distincts √ 3.𝚽 , en 360 paires parallèles, distants de √ 0.𝚫 .

Les √ 4 cordes se produisent à 60 diamètres de long (75 ensembles de 4 axes orthogonaux), les rayons 120 longue de 600 cellules. Les cordes √ 4 joignent des sommets opposés qui sont distants de cinq arêtes √ 0.𝚫 sur un grand cercle géodésique. Il existe 25 ensembles distincts mais se chevauchant de 12 diamètres, chacun comprenant l'une des 25 24 cellules inscrites.

La somme des longueurs au carré de toutes ces cordes distinctes de la cellule 600 est de 14 400 = 120 ² . Ce sont tous les polygones centraux passant par des sommets, mais la cellule 600 a un polygone central remarquable qui ne passe par aucun sommet. De plus, dans l'espace 4, il existe des géodésiques sur la sphère 3 qui ne se trouvent pas du tout dans des plans centraux. Il existe des chemins géodésiques les plus courts entre deux sommets de 600 cellules qui sont hélicoïdaux plutôt que simplement circulaires ; ils correspondant à isoclinic (diagonale) rotations plutôt que de simples rotations.

Tous les polygones géodésiques énumérés ci-dessus se situent dans des plans centraux de trois types seulement, chacun caractérisé par un angle de rotation : les plans décagones (??/5 à part), des plans hexagonaux (??/3 à part, également dans chacune des 25 24 cellules inscrites), et des plans carrés (??/2à part, également dans chacune des 75 cellules inscrites). Ces plans centraux de la cellule 600 peuvent être divisés en 4 hyperplans centraux (3 espaces) formant chacun un icosidodécaèdre . Il y a 450 grands carrés séparés de 90 degrés ; 200 grands hexagones distants de 60 degrés ; et 72 grands décagones distants de 36 degrés. Chaque grand plan carré est complètement orthogonal à un autre grand plan carré. Chaque grand plan hexagonal est complètement orthogonal à un plan qui coupe seulement deux sommets (une √ 4 de grand diamètre): un grand digone plan. Chaque grand plan décagone est complètement orthogonal à un plan qui ne coupe aucun sommet : un grand plan de 30gones .

Fibration

Chaque ensemble de polygones de grands cercles similaires (carrés ou hexagones ou décagones) peut être divisé en faisceaux de grands cercles parallèles de Clifford sans intersection (de 30 carrés ou 20 hexagones ou 12 décagones). Chaque faisceau de fibres des grands cercles parallèles de Clifford est une fibration de Hopf discrète qui remplit les 600 cellules, visitant les 120 sommets une seule fois. Les polygones du grand cercle de chaque faisceau s'enroulent en spirale, délimitant des anneaux hélicoïdaux de cellules face-collées qui s'emboîtent les unes dans les autres, se traversent sans se croiser dans aucune cellule et remplissent exactement les 600 cellules avec leurs ensembles de cellules disjointes. Les différents faisceaux de fibres avec leurs anneaux de cellules remplissent chacun le même espace (la cellule 600) mais leurs fibres sont parallèles à Clifford dans différentes « directions » ; les polygones de grand cercle dans différentes fibrations ne sont pas parallèles à Clifford.

Décagones

Les fibrations de la cellule 600 comprennent 6 fibrations de ses 72 grands décagones : 6 faisceaux de fibres de 12 grands décagones. Chaque faisceau de fibres délimite 20 anneaux hélicoïdaux de 30 cellules tétraédriques chacun, avec cinq anneaux s'emboîtant autour de chaque décagone. Chaque cellule tétraédrique occupe un seul anneau cellulaire dans chacune des 6 fibrations. La cellule tétraédrique contribue chacun de ses 6 bords à un décagone dans une fibration différente, mais contribue à ce bord à cinq anneaux cellulaires distincts dans la fibration.

Hexagones

Les fibrations des 24 cellules comprennent 4 fibrations de ses 16 grands hexagones : 4 faisceaux de fibres de 4 grands hexagones. Chaque faisceau de fibres délimite 4 anneaux hélicoïdaux de 6 cellules octaédriques chacun, avec trois anneaux s'emboîtant autour de chaque hexagone. Chaque cellule octaédrique n'occupe qu'un anneau cellulaire dans chacune des 4 fibrations. La cellule octaédrique contribue à 3 de ses 12 arêtes à 3 hexagones parallèles de Clifford différents dans chaque fibration, mais contribue chaque arête à trois anneaux cellulaires distincts dans la fibration. La cellule 600 contient 25 cellules 24 et peut être considérée comme un composé de 5 cellules 24 disjointes. Il a 10 fibrations de ses 200 grands hexagones : 10 faisceaux de fibres de 20 grands hexagones. Chaque faisceau de fibres délimite 20 anneaux hélicoïdaux de 6 cellules octaédriques chacun, avec trois anneaux s'emboîtant autour de chaque hexagone. Chaque cellule octaédrique n'occupe qu'un anneau cellulaire dans chacune des 10 fibrations.

Carrés

Les fibrations de la cellule 16 comprennent 3 fibrations de ses 6 grands carrés : 3 faisceaux de fibres de 2 grands carrés. Chaque faisceau de fibres délimite 2 anneaux hélicoïdaux de 8 cellules tétraédriques chacun. Chaque cellule tétraédrique occupe un seul anneau cellulaire dans chacune des 3 fibrations. La cellule tétraédrique contribue à chacun de ses 6 bords à un carré dans une fibration différente, mais contribue à ce bord aux deux anneaux cellulaires distincts de la fibration. La cellule 600 contient 75 cellules 16 et peut être considérée comme un composé de 15 cellules 16 disjointes. Il a 15 fibrations de ses 450 grands carrés : 15 faisceaux de fibres de 30 grands carrés. Chaque faisceau de fibres délimite 150 anneaux hélicoïdaux de 8 cellules tétraédriques chacun. Chaque cellule tétraédrique occupe un seul anneau cellulaire dans chacune des 15 fibrations.

Cadres de référence

Parce que chaque 16-cellules constitue une base orthonormée pour le choix d'un référentiel de coordonnées , les fibrations de 16-cellules différentes ont des référentiels naturels différents. Les 15 fibrations de grands carrés du 600-cell correspondent aux 15 référentiels naturels du 600-cell. Un ou plusieurs de ces référentiels sont naturels à chaque fibration du 600-cell. Chaque fibration de grands hexagones a trois (également naturels) de ces cadres de référence (comme les 24 cellules ont 3 16 cellules) ; chaque fibration des grands décagones a tous les 15 (comme la cellule 600 a 15 cellules 16 disjointes).

Anneaux de cellules parallèles Clifford

Les anneaux cellulaires hélicoïdaux densément entassés des fibrations sont disjoints entre les cellules, mais ils partagent des sommets, des arêtes et des faces. Chaque fibration de la cellule 600 peut être considérée comme un emballage dense d'anneaux cellulaires avec les faces correspondantes des anneaux cellulaires adjacents liées les unes aux autres. La même fibration peut également être considérée comme un arrangement clairsemé minimal de moins d' anneaux cellulaires complètement disjoints qui ne se touchent pas du tout.

Les fibrations des grands décagones peuvent être vues (de cinq manières différentes) comme 4 anneaux cellulaires tétraédriques complètement disjoints avec des espaces les séparant, plutôt que comme 20 anneaux cellulaires liés par le visage, en omettant tous les anneaux cellulaires sauf un des cinq qui se rencontrent à chaque décagone. Les cinq différentes manières de procéder sont équivalentes, en ce sens que toutes les cinq correspondent à la même fibration discrète (dans le même sens que les 12 fibrations à 600 cellules sont équivalentes, en ce sens que toutes les 12 couvrent la même cellule à 600). Les 4 anneaux de cellules constituent toujours la fibration complète : ils incluent les 12 décagones parallèles de Clifford, qui visitent les 120 sommets. Ce sous-ensemble de 4 des 20 anneaux de cellules est dimensionnellement analogue au sous-ensemble de 12 des 72 décagones, en ce que les deux sont des ensembles de polytopes parallèles de Clifford complètement disjoints qui visitent les 120 sommets. Le sous-ensemble de 4 des 20 anneaux cellulaires est l'une des 5 fibrations au sein de la fibration de 12 des 72 décagones : une fibration d'une fibration. Toutes les fibrations ont cette structure à deux niveaux avec des sous- fibrations .

Les fibrations des grands hexagones des 24 cellules peuvent être vues (de trois manières différentes) comme 2 anneaux cellulaires complètement disjoints avec des espaces les séparant, plutôt que comme 4 anneaux cellulaires liés par le visage, en omettant tous les anneaux cellulaires sauf un des trois qui se rencontrent à chaque hexagone. Par conséquent, chacune des 10 fibrations des grands hexagones des 600 cellules peut être considérée comme 2 anneaux de cellules octaédriques complètement disjoints.

Les fibrations des grands carrés des 16 cellules peuvent être vues (de deux manières différentes) comme un anneau cellulaire unique avec un espace vide adjacent de la taille d'un anneau cellulaire, plutôt que comme 2 anneaux cellulaires liés par le visage, en omettant l'un des deux anneaux de cellules qui se rencontrent à chaque carré. Par conséquent, chacune des 15 fibrations des grands carrés des 600 cellules peut être considérée comme un seul anneau de cellules tétraédriques.

Les constructions clairsemées des fibrations de 600 cellules correspondent à des décompositions de symétrie inférieure des cellules de 600, 24 ou 16 cellules avec des cellules de couleurs différentes pour distinguer les anneaux cellulaires des espaces entre eux. La forme particulière de symétrie inférieure de la cellule 600 correspondant à la construction clairsemée des grandes fibrations décagones est dimensionnellement analogue à la forme tétraèdre retroussée de l'icosaèdre (qui est la base de ces fibrations sur la 2-sphère). Chacun des 4 anneaux cellulaires de Boerdijk-Coxeter complètement disjoints est soulevé d'une face correspondante de l'icosaèdre.

Bâtiments

La cellule 600 incorpore les géométries de chaque polytope régulier convexe dans les quatre premières dimensions, à l'exception des cellules 5, 120 et des polygones {7} et plus. Par conséquent, il existe de nombreuses façons de construire ou de déconstruire la cellule 600, mais aucune d'entre elles n'est triviale. La construction du 600 cellules par rapport à son prédécesseur régulier, le 24 cellules, peut être difficile à visualiser.

La construction de Gosset

Thorold Gosset a découvert les 4-polytopes semi-réguliers , y compris le snub 24-cell avec 96 sommets, qui se situe entre le 24-cell et le 600-cell dans la séquence de 4-polytopes convexes de taille et de complexité croissantes dans le même rayon. La construction par Gosset des 600 cellules à partir des 24 cellules se fait en deux étapes, en utilisant le snub 24 cellules comme forme intermédiaire. Dans la première étape, plus complexe (décrite ailleurs ), le snub 24-cell est construit par une troncature snub spéciale d'un 24-cell au niveau des sections dorées de ses bords. Dans la deuxième étape, le 600-cell est construit de manière simple en ajoutant 4 pyramides (sommets) aux facettes du snub 24-cell.

Le snub 24-cell est une diminution de 600 cellules à partir de laquelle 24 sommets (et le groupe de 20 cellules tétraédriques autour de chacun) ont été tronqués, laissant une cellule icosaédrique « plate » à la place de chaque pyramide icosaédrique supprimée. Le snub 24-cell a donc 24 cellules icosaédriques et les 120 cellules tétraédriques restantes. La deuxième étape de la construction par Gosset de la cellule 600 est simplement l'inverse de cette diminution : une pyramide icosaédrique de 20 cellules tétraédriques est placée sur chaque cellule icosaédrique.

La construction de la cellule de rayon unitaire 600 à partir de son précurseur la cellule de rayon unitaire 24 par la méthode de Gosset nécessite en fait trois étapes. Le précurseur à 24 cellules de la cellule snub-24 n'a pas le même rayon : il est plus grand, puisque la cellule snub-24 est sa troncature. En commençant par les 24 cellules de rayon unitaire, la première étape consiste à l' inverser autour de sa sphère médiane pour construire son double canonique extérieur : une plus grande 24 cellules, puisque les 24 cellules sont auto-duales. Ces 24 cellules plus grandes peuvent ensuite être tronquées en une cellule de 24 cellules de rayon unitaire.

Amas de cellules

Puisqu'elle est si indirecte, la construction de Gosset peut ne pas nous aider beaucoup à visualiser directement comment les 600 cellules tétraédriques s'emboîtent dans une enveloppe de surface tridimensionnelle, ou comment elles se trouvent sur l'enveloppe de surface sous-jacente des cellules octaédriques de 24 cellules. Pour cela, il est utile de construire les 600 cellules directement à partir d'amas de cellules tétraédriques.

La plupart d'entre nous ont des difficultés à visualiser les 600 cellules de l'extérieur dans un espace à 4 dimensions, ou à reconnaître une vue extérieure de la cellule à 600 en raison de notre manque total d'expérience sensorielle dans des espaces à 4 dimensions, mais nous devrions être capables de visualiser le enveloppe de surface de 600 cellules de l'intérieur parce que ce volume est un espace tridimensionnel dans lequel nous pourrions réellement « nous promener » et explorer. Dans ces exercices de construction de 600 cellules à partir d'amas de cellules, nous sommes entièrement dans un espace tridimensionnel, bien qu'il s'agisse d'un espace courbe fermé étrangement petit , dans lequel nous pouvons nous éloigner de seulement dix longueurs de bord en ligne droite dans n'importe quel direction et retour à notre point de départ.

Icosaèdre

Un icosaèdre régulier coloré en symétrie d' octaèdre adoucie. Les icosaèdres des 600 cellules sont face à face collés les uns aux autres sur les faces jaunes, et à des amas de 5 cellules tétraédriques sur les faces bleues. Le sommet de la pyramide icosaédrique (non visible) est un 13e sommet de 600 cellules à l'intérieur de l'icosaèdre (mais au-dessus de son hyperplan).

Un amas de 5 cellules tétraédriques : quatre cellules liées par face autour d'une cinquième cellule (non visible). Les quatre cellules se trouvent dans des hyperplans différents.

La figure de sommet de la cellule 600 est l' icosaèdre . Vingt cellules tétraédriques se rencontrent à chaque sommet, formant une pyramide icosaédrique dont le sommet est le sommet, entouré de son icosaèdre de base. La cellule 600 a un angle dièdre de??/3 + arccos(−1/4) 164,4775° .

Un ensemble de 600 cellules peut être assemblé à partir de 24 pyramides icosaédriques de ce type (collées face à face sur 8 des 20 faces de l'icosaèdre, colorées en jaune dans l'illustration), plus 24 groupes de 5 cellules tétraédriques (quatre cellules face-collées autour d'un) qui comblent les vides restant entre les icosaèdres. Chaque icosaèdre est lié face à chaque groupe adjacent de 5 cellules par deux faces bleues qui partagent une arête (qui est également l'une des six arêtes du tétraèdre central des cinq). Six groupes de 5 cellules entourent chaque icosaèdre et six icosaèdres entourent chaque groupe de 5 cellules. Cinq cellules tétraédriques entourent chaque bord de l'icosaèdre : deux de la pyramide icosaédrique et trois d'un groupe de 5 cellules (dont l'une est le tétraèdre central des cinq).

Les sommets des 24 pyramides icosaédriques sont les sommets de 24 cellules inscrites dans les 600 cellules. Les 96 autres sommets (les sommets des icosaèdres) sont les sommets d'un snub inscrit 24 cellules , qui a exactement la même structure d'icosaèdres et de tétraèdres décrits ici, sauf que les icosaèdres ne sont pas des pyramides à 4 remplies par des cellules tétraédriques ; ce ne sont que des cellules icosaédriques tridimensionnelles "plates".

La coloration des icosaèdres avec 8 faces jaunes et 12 faces bleues peut se faire de 5 manières distinctes. Ainsi, le sommet du sommet de chaque pyramide icosaédrique est un sommet de 5 24 cellules distinctes, et les 120 sommets comprennent 25 (et non 5) 24 cellules.

Les icosaèdres sont liés en face en "lignes droites" géodésiques par leurs faces opposées, pliées dans la quatrième dimension en un anneau de 6 pyramides icosaédriques. Leurs sommets sont les sommets d'un grand hexagone circulaire . Cette géodésique hexagonale traverse un anneau de 12 cellules tétraédriques, alternativement liées face à face et sommet à sommet. Le grand diamètre de chaque paire de tétraèdres à face collée (chaque bipyramide triangulaire ) est un bord hexagonal (un bord à 24 alvéoles). Il y a 4 anneaux de verrouillage disjoints de 6 icosaèdres, tout comme il y a 4 anneaux de verrouillage disjoints de 6 octaèdres dans les 24 cellules (une fibration hexagonale ).

Les cellules tétraédriques sont liées en face en triple hélice , pliées dans la quatrième dimension en anneaux de 30 cellules tétraédriques. Les trois hélices sont des "lignes droites" géodésiques de 10 arêtes : des décagones de grand cercle qui courent Clifford parallèlement les uns aux autres. Chaque tétraèdre, ayant six arêtes, participe à six décagones différents et ainsi à l'ensemble des 6 fibrations décagonales de la cellule 600 .

La partition des 600 cellules en grappes de 20 cellules et en grappes de 5 cellules est artificielle, puisque toutes les cellules sont les mêmes. On peut commencer par choisir un groupe de pyramides icosaédriques centré sur n'importe quel sommet choisi arbitrairement, il y a donc 120 icosaèdres qui se chevauchent dans les 600 cellules. Leurs 120 sommets sont chacun un sommet de cinq 24-vertex 24-cells, donc il y a 5*120/24 = 25 24-cells qui se chevauchent.

Octaèdre

Il existe un autre moyen utile de diviser la surface des 600 cellules en 24 groupes de 25 cellules tétraédriques, ce qui révèle plus de structure et une construction directe des 600 cellules par rapport à son prédécesseur, les 24 cellules.

Commencez par l'un des groupes de 5 cellules (ci-dessus) et considérez sa cellule centrale comme l'objet central d'un nouveau groupe plus grand de cellules tétraédriques. La cellule centrale est la première section des 600 cellules commençant par une cellule. En l'entourant de cellules plus tétraédriques, nous pouvons atteindre les sections plus profondes en commençant par une cellule.

Tout d' abord, notez que un groupe de 5 cellules se compose de 4 paires se chevauchant de tétraèdres liés face ( dipyramids triangulaires ) dont le grand diamètre est un bord 24 cellules (une arête de l' hexagone) de longueur √ 1 . Six dipyramids plus triangulaires se placent dans les concavités sur la surface du groupe de 5, de sorte que les cordes extérieures reliant les 4 sommets apicaux sont également des bords 24 des cellules de longueur √ 1 . Ils forment un tétraèdre de longueur d'arête √ 1 , qui est la deuxième section de début de cellule 600 avec une cellule. Il y a 600 de ces √ 1 sections tétraèdres dans 600 cellules.

Avec les six dipyramides triangulaires insérés dans les concavités, il y a 12 nouvelles cellules et 6 nouveaux sommets en plus des 5 cellules et 8 sommets de l'amas d'origine. Les 6 nouveaux sommets forment la troisième section de début de cellule 600 avec une cellule, un octaèdre de longueur d'arête √ 1 , de toute évidence la cellule d'une 24 cellule. Comme partiellement rempli jusqu'à présent (par 17 cellules tétraédriques), cette √ 1 octaèdre présente des faces concaves dans lequel une courte unique de pyramide triangulaire; il a le même volume qu'une cellule tétraédrique régulière mais une forme tétraédrique irrégulière. Chaque cellule octaédrique se compose de 1 + 4 + 12 + 8 = 25 cellules tétraédriques : 17 cellules tétraédriques régulières plus 8 cellules tétraédriques volumétriquement équivalentes constituées chacune de 6 fragments d'un sixième de 6 cellules tétraédriques régulières différentes qui s'étendent chacune sur trois cellules octaédriques adjacentes.

Ainsi la cellule de rayon unitaire 600 est construite directement à partir de son prédécesseur, la cellule de rayon unitaire 24, en plaçant sur chacune de ses facettes octaédriques une pyramide octaédrique irrégulière tronquée de 14 sommets construite (de la manière ci-dessus) à partir de 25 cellules tétraédriques régulières cellules de longueur de bord 1/?? 0,618.

Union de deux tores

Il existe encore un autre moyen utile de diviser la surface des 600 cellules en amas de cellules tétraédriques, ce qui révèle plus de structure et les fibrations décagonales des 600 cellules. Un ensemble de 600 cellules peut être assemblé à partir de 2 anneaux de 5 pyramides icosaédriques, liés sommet à sommet en "lignes droites" géodésiques, plus 40 anneaux de 10 cellules qui remplissent les vides restant entre les icosaèdres.

100 tétraèdres dans un réseau 10 × 10 formant une frontière de tore de Clifford dans la cellule 600. Ses bords opposés sont identifiés, formant un duocylindre .

La cellule 120 peut être décomposée en deux tores disjoints . Puisqu'il s'agit du dual du 600-cell, cette même structure double tori existe dans le 600-cell, bien qu'elle soit un peu plus complexe. Le chemin géodésique à 10 cellules dans la cellule 120 correspond au chemin décagone à 10 sommets dans la cellule 600.

Commencez par assembler cinq tétraèdres autour d'une arête commune. Cette structure ressemble un peu à une "soucoupe volante" angulaire. Empilez dix d'entre eux, sommet à sommet, style "crêpe". Remplissez l'anneau annulaire entre chaque paire de "soucoupes volantes" avec 10 tétraèdres pour former un icosaèdre. Vous pouvez voir cela comme cinq pyramides icosaédriques empilées à sommets , avec les cinq espaces annulaires supplémentaires également remplis. La surface est la même que celle de dix antiprismes pentagonaux empilés : une colonne à face triangulaire avec une section transversale pentagonale. Courbé en un anneau colonnaire, il s'agit d'un tore composé de 150 cellules, de dix arêtes de long, avec 100 faces triangulaires exposées, 150 arêtes exposées et 50 sommets exposés. Empilez un autre tétraèdre sur chaque face exposée. Cela vous donnera un tore quelque peu bosselé de 250 cellules avec 50 sommets surélevés, 50 sommets de vallée et 100 bords de vallée. Les vallées sont des chemins fermés longs de 10 bords et correspondent à d'autres instances du chemin décagone à 10 sommets mentionné ci-dessus (décagones des grands cercles). Ces décagones tournent en spirale autour du décagone central, mais mathématiquement, ils sont tous équivalents (ils se trouvent tous dans des plans centraux).

Construisez un deuxième tore identique de 250 cellules qui s'interconnecte avec le premier. Cela représente 500 cellules. Ces deux tores s'accouplent avec les sommets de la vallée touchant les sommets surélevés, laissant 100 vides tétraédriques qui sont remplis des 100 tétraèdres restants qui s'accouplent aux bords de la vallée. Ce dernier ensemble de 100 tétraèdres se trouve à la limite exacte du duocylindre et forme un tore de Clifford . Ils peuvent être "déroulés" dans un tableau carré 10x10. Incidemment, cette structure forme une couche tétraédrique dans le nid d'abeille tétraédrique-octaédrique . Il y a exactement 50 évidements et pics de "caisse à œufs" des deux côtés qui s'accouplent avec les tores de 250 cellules. Dans ce cas, dans chaque évidement, au lieu d'un octaèdre comme dans le nid d'abeille, s'insère une bipyramide triangulaire composée de deux tétraèdres.

Cette décomposition de la cellule 600 a une symétrie [[10,2 ⁺ ,10]], d'ordre 400, la même symétrie que le grand antiprisme . Le grand antiprisme n'est que la cellule de 600 avec les deux tores de 150 cellules ci-dessus supprimés, ne laissant que la seule couche médiane de 300 tétraèdres, dimensionnellement analogue à la ceinture à 10 faces d'un icosaèdre avec les 5 faces supérieure et 5 inférieures supprimées ( un antiprisme pentagonal ).

Les deux tores de 150 cellules contiennent chacun 6 grands décagones parallèles à Clifford (cinq autour d'un), et les deux tores sont parallèles à Clifford, donc ensemble, ils constituent une fibration complète de 12 décagones qui atteint les 120 sommets, bien qu'ils ne remplissent que la moitié le 600-cell avec des cellules.

Un seul anneau d' hélice Boerdijk-Coxeter de 30 tétraèdres dans les 600 cellules, vu en projection stéréographique.

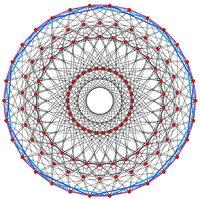Un anneau de 30 tétraèdres peut être vu le long du périmètre de cette projection orthogonale de 30 gones.

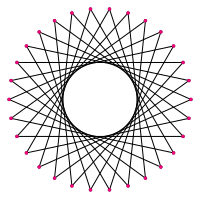Les 30 sommets de l'anneau de 30 cellules se trouvent sur une étoile oblique de 30 gon avec un nombre d'enroulement de 11.

La cellule 600 peut également être divisée en 20 anneaux entrelacés disjoints de 30 cellules, chacun de dix bords de long, formant une fibration de Hopf discrète qui remplit la totalité de la cellule 600. Ces chaînes de 30 tétraèdres forment chacune une hélice de Boerdijk-Coxeter . L'axe central de chaque hélice est une géodésique de 30 gons qui ne coupe aucun sommet, et les 30 sommets de l'anneau de 30 cellules forment une étoile asymétrique de 30 gones avec une orbite géodésique qui s'enroule 11 fois autour des 600 cellules. Cinq de ces hélices à 30 cellules s'emboîtent ensemble et s'enroulent en spirale autour de chacun des trajets du décagone à 10 sommets, formant le tore à 150 cellules décrit ci-dessus. Ainsi, chaque grand décagone est le décagone central d'un tore à 150 cellules.

Les 20 anneaux de 30 cellules disjoints constituent quatre tores identiques de 150 cellules disjoints : les deux décrits dans la grande décomposition antiprisme ci-dessus, et deux autres qui remplissent la couche médiane de 300 tétraèdres occupés par 30 anneaux de 10 cellules dans le grande décomposition antiprisme. Les quatre anneaux de 150 cellules s'enroulent en spirale et se traversent de la même manière que les 20 anneaux de 30 cellules ou les 12 grands décagones ; ces trois ensembles de polytopes parallèles de Clifford sont la même fibration décagonale discrète du 600-cell .

Rotations

Les 4-polytopes convexes réguliers sont une expression de leur symétrie sous-jacente qui est connue sous le nom de SO(4) , le groupe de rotations autour d'un point fixe dans l'espace euclidien à 4 dimensions.

Le 600-cell est généré par les rotations isocliniques du 24-cell de 36° =??/5 (l'arc d'une longueur de bord de 600 cellules).

Il y a 25 24 cases inscrites dans les 600 cases. Par conséquent, il y a également 25 cellules snub inscrites, 75 tesseracts inscrits et 75 cellules 16 inscrites.

La cellule à 8 sommets et 16 alvéoles a 4 diamètres longs inclinés à 90° = ??/2les uns aux autres, souvent pris comme les 4 axes orthogonaux ou la base du système de coordonnées.

Le 24-vertex 24-cell a 12 longs diamètres inclinés à 60° = ??/3 l'un à l'autre : 3 ensembles disjoints de 4 axes orthogonaux, chaque ensemble comprenant les diamètres de l'une des 3 cellules inscrites à 16, tournées de manière isoclinique de ??/3 l'un par rapport à l'autre.

La cellule à 120 sommets de 600 a 60 diamètres longs : pas seulement 5 ensembles disjoints de 12 diamètres, chacun comprenant l'un des 5 24 cellules inscrites (comme on pourrait le soupçonner par analogie), mais 25 ensembles distincts mais se chevauchant de 12 diamètres, chacun comprenant l'une des 25 24 cellules inscrites. Il y a 5 24-cellules disjointes dans la 600-cell, mais pas seulement 5 : il y a 10 façons différentes de partitionner la 600-cell en 5 24-cellules disjointes.

Comme les 16 cellules et les 8 cellules inscrites dans les 24 cellules, les 25 24 cellules inscrites dans les 600 cellules sont des polytopes mutuellement isocliniques . La distance de rotation entre les 24 cellules inscrites est toujours une rotation à angle égal de??/5 dans chaque paire de plans de rotation invariants complètement orthogonaux.

Un anneau en 4 dimensions de trois grands décagones parallèles Clifford, coupés et disposés à plat dans un espace en 3 dimensions.

Cinq 24-cellules sont disjointes parce qu'elles sont parallèles à Clifford : leurs sommets correspondants sont ??/5 à part sur deux grands cercles décagonaux parallèles non sécants de Clifford (ainsi que ??/5à part sur le même grand cercle décagonal). Une rotation isocline des plans décagonaux par??/5prend chaque 24 cellules à une 24 cellules disjointes (tout comme une rotation isocline de plans hexagonaux par??/3prend chaque 16-cellule à une 16-cellule disjointe). Chaque rotation isocline se produit sous deux formes chirales : il y a 4 24 cellules disjointes à gauche de chaque 24 cellules et 4 autres 24 cellules disjointes à sa droite . Les rotations gauche et droite atteignent 24 cellules différentes ; par conséquent, chaque 24 cellules appartient à deux ensembles différents de cinq 24 cellules disjointes.

Tous les polytopes parallèles de Clifford sont isocliniques, mais tous les polytopes isocliniques ne sont pas des parallèles de Clifford (objets complètement disjoints). Chaque 24 cellules est isocline et Clifford parallèle à 8 autres, et isocline mais pas Clifford parallèle à 16 autres. Avec chacun des 16, il partage 6 sommets : un plan central hexagonal. Les 24 cellules non disjointes sont reliées par une simple rotation de??/5dans un plan invariant coupant seulement deux sommets de la cellule 600, une rotation dans laquelle le plan fixe complètement orthogonal est leur plan central hexagonal commun. Ils sont également liés par une rotation isocline dans laquelle les deux plans tournent de??/5.

Il existe deux sortes de ??/5rotations isocliniques qui amènent chaque 24 cellules à une autre 24 cellules. Les 24 cellules disjointes sont liées par un??/5rotation isoclinique d'une fibration entière de 12 plans invariants décagonaux parallèles de Clifford . (Il y a 6 de ces ensembles de fibres, et une rotation isocline droite ou gauche possible avec chaque ensemble, il y a donc 12 rotations distinctes.) Les 24 cellules non disjointes sont liées par un??/5rotation isoclinique d'une fibration entière de 20 plans invariants hexagonaux parallèles de Clifford . (Il existe 10 de ces ensembles de fibres, il y a donc 20 rotations distinctes.)

D'autre part, chacun des 10 ensembles de cinq 24 cellules disjointes est parallèle à Clifford parce que ses grands hexagones correspondants sont parallèles à Clifford. (Les 24 cellules n'ont pas de grands décagones.) Les 16 grands hexagones de chaque 24 cellules peuvent être divisés en 4 ensembles de 4 géodésiques parallèles de Clifford sans intersection , dont chaque ensemble couvre les 24 sommets des 24 cellules. Les 200 grands hexagones de la cellule 600 peuvent être divisés en 10 ensembles de 20 géodésiques parallèles de Clifford sans intersection , dont chaque ensemble couvre les 120 sommets de la cellule 600. Chacun des 10 ensembles de 20 hexagones disjoints peut être divisé en cinq ensembles de 4 hexagones disjoints, chaque ensemble de 4 couvrant une 24 cellules disjointes. De même, les grands carrés correspondants de 24 cellules disjointes sont parallèles à Clifford.

Triangles d'or radiaux

La cellule 600 peut être construite radialement à partir de 720 triangles d'or de longueurs d'arête √ 0.𝚫 √ 1 √ 1 qui se rencontrent au centre du polytope 4, chacun contribuant à deux rayons √ 1 et à une arête √ 0.𝚫 . Ils forment 1200 pyramides triangulaires avec leurs sommets au centre : des tétraèdres irréguliers à bases équilatérales √ 0.𝚫 (les faces des 600 cellules). Ceux-ci forment 600 pyramides tétraédriques avec leurs sommets au centre : 5 cellules irrégulières avec des bases tétraédriques régulières √ 0.𝚫 (les cellules de la cellule 600).

En tant que configuration

Cette matrice de configuration représente les 600 cellules. Les lignes et les colonnes correspondent aux sommets, aux arêtes, aux faces et aux cellules. Les nombres diagonaux indiquent combien de chaque élément se produit dans l'ensemble des 600 cellules. Les nombres non diagonaux indiquent combien d'éléments de la colonne se trouvent dans ou au niveau de l'élément de la ligne.

${\displaystyle {\begin{bmatrix}{\begin{matrix}120&12&30&20\\2&720&5&5\\3&3&1200&2\\4&6&4&600\end{matrix}}\end{bmatrix}}}$

Voici la configuration étendue avec k éléments de visage et k figures. Le nombre d'éléments diagonaux est le rapport de l'ordre complet du groupe Coxeter , 14400, divisé par l'ordre du sous-groupe avec suppression du miroir.

H 4		k- visage	f k	f 0	f 1	f 2	f 3	k -figue	Remarques
H 3		( )	f 0	120	12	30	20	{3,5}	H 4 /H 3 = 14400/120 = 120
A 1 H 2		{ }	f 1	2	720	5	5	{5}	H 4 /H 2 A 1 = 14400/10/2 = 720
Un 2 Un 1		{3}	f 2	3	3	1200	2	{ }	H 4 /A 2 A 1 = 14400/6/2 = 1200
Un 3		{3,3}	f 3	4	6	4	600	( )	H 4 /A 3 = 14400/24 ​​= 600

Symétries

Les icosiennes sont un ensemble spécifique de quaternions hamiltoniens avec la même symétrie que la cellule 600. Les icosiennes se situent dans le champ d' or , ( a + b √ 5 ) + ( c + d √ 5 ) i + ( e + f √ 5 ) j + ( g + h √ 5 ) k , où les huit variables sont des nombres rationnels . Les sommes finies des 120 unités icosiennes sont appelées l' anneau icosien .

Interprétés comme des quaternions , les 120 sommets des 600 cellules forment un groupe sous multiplication quaternionique. Ce groupe est souvent appelé groupe icosaédrique binaire et noté 2I car il s'agit de la double couverture du groupe icosaédrique ordinaire I . Il apparaît deux fois dans le groupe de symétrie de rotation RSG de la cellule 600 en tant que sous - groupe invariant , à savoir en tant que sous-groupe 2I _L des multiplications à gauche des quaternions et en tant que sous-groupe 2I _R des multiplications à droite des quaternions. Chaque symétrie de rotation de la cellule 600 est générée par des éléments spécifiques de 2I _L et 2I _R ; la paire d'éléments opposés génère le même élément de RSG . Le centre de RSG est constitué de la non-rotation Id et de l'inversion centrale −Id . On a l'isomorphisme RSG ≅ (2I _L × 2I _R ) / {Id, -Id} . L'ordre de RSG est égal à120 × 120/2 = 7200.

Le groupe binaire icosaédrique est isomorphe à SL(2,5) .

Le groupe de symétrie complet de la cellule 600 est le groupe Weyl de H ₄ . Il s'agit d'un groupe d'ordre 14400. Il se compose de 7200 rotations et 7200 rotations-réflexions. Les rotations forment un sous - groupe invariant du groupe de symétrie complète. Le groupe de symétrie de rotation a été décrit par SL van Oss.

Visualisation

Les symétries de la surface 3-D de la cellule 600 sont quelque peu difficiles à visualiser en raison à la fois du grand nombre de cellules tétraédriques et du fait que le tétraèdre n'a pas de faces ou de sommets opposés. On peut commencer par réaliser que le 600-cell est le double du 120-cell. On peut également remarquer que la cellule 600 contient également les sommets d'un dodécaèdre, qui avec un certain effort peut être vu dans la plupart des projections en perspective ci-dessous.

Projection 2D

La projection décagonale H3 montre le plan du polygone de van Oss .

Projections orthographiques par plans de Coxeter

H 4	-	F 4
[30] (Rouge=1)	[20] (Rouge=1)	[12] (Rouge=1)
H 3	A 2 / B 3 / D 4	A 3 / B 2
[10] (Rouge=1,orange=5,jaune=10)	[6] (Rouge=1,orange=3,jaune=6)	[4] (Rouge=1,orange=2,jaune=4)

Projection 3D

Un modèle tridimensionnel de la cellule 600, dans la collection de l' Institut Henri Poincaré , a été photographié en 1934-1935 par Man Ray , et faisait partie de deux de ses peintures ultérieures « Équation de Shakespeare ».

Projection vertex d'abord
	Cette image montre une projection en perspective du sommet d'abord de la cellule 600 en 3D. La cellule 600 est mise à l'échelle avec un rayon de centre de sommet de 1 et le point de vue 4D est placé à 5 unités de distance. Ensuite, les améliorations suivantes sont appliquées : Les 20 tétraèdres se rencontrant au sommet le plus proche du point de vue 4D sont rendus en couleur unie. Leur disposition icosaédrique est clairement indiquée. Les tétraèdres adjacents immédiatement à ces 20 cellules sont rendus en jaune transparent. Les cellules restantes sont rendues en contour de bord. Les cellules opposées au point de vue 4D (celles situées de l'autre côté de la cellule 600) ont été supprimées afin de réduire l'encombrement visuel dans l'image finale.
Projection cellule d'abord
	Cette image montre la projection en perspective de 600 cellules en première cellule en 3D. Encore une fois, les 600 cellules à un rayon de centre de sommet de 1 et le point de vue 4D sont placés à 5 unités de distance. Les améliorations suivantes sont alors appliquées : La cellule la plus proche du point de vue 4D est rendue en couleur unie, située au centre de l'image de projection. Les cellules qui l'entourent (partageant au moins 1 sommet) sont rendues en jaune transparent. Les cellules restantes sont rendues en contour de bord. Les cellules opposées au point de vue 4D ont été sélectionnées pour plus de clarté. Ce point de vue particulier montre un joli contour de 5 tétraèdres partageant un bord, vers l'avant de l'image 3D.

Projections isométriques orthogonales (gauche) et perspective (droite) synchronisées avec le cadre
Lire les médias

600 cellules diminuées

Le snub 24-cell peut être obtenu à partir du 600-cell en supprimant les sommets d'un 24-cell inscrit et en prenant l' enveloppe convexe des sommets restants. Ce processus est une diminution des 600 cellules.

Le grand antiprisme peut être obtenu par une autre diminution de la cellule 600 : en supprimant 20 sommets qui reposent sur deux anneaux mutuellement orthogonaux et en prenant l'enveloppe convexe des sommets restants.

Un 600-cellules bi-24-diminué, avec toutes les cellules d' icosaèdre tridiminués a 48 sommets supprimés, laissant 72 des 120 sommets du 600-cell. Le double d'un 600-cellules bi-24-diminué, est un tri-24-diminué 600-cellule, avec 48 sommets et 72 cellules hexaèdres.

Il y a un total de 314 248 344 diminutions de la cellule 600 par des sommets non adjacents. Tous sont constitués de cellules tétraédriques et icosaédriques régulières.

600 cellules diminuées
Nom	Tri-24-diminué 600 cellules	Bi-24-diminué 600 cellules	Snub 24 cellules (24 cellules réduites à 600 cellules)	Grand antiprisme ( 20-600 cellules diminuées)	600 cellules
Sommets	48	72	96	100	120
Figure de sommet (Symétrie)	dual d'icosaèdre tridiminué ([3], ordre 6)	anticoin tétragonal ([2] + , ordre 2)	icosaèdre tridiminué ([3], ordre 6)	icosaèdre bidiminé ([2], ordre 4)	Icosaèdre ([5,3], ordre 120)
Symétrie	Commandez 144 (48×3 ou 72×2)		[3 + ,4,3] Ordre 576 (96×6)	[[10,2 + ,10]] Commande 400 (100×4)	[5,3,3] Commande 14400 (120×120)
Rapporter
Ortho H 4 avion
Ortho F 4 avion

Polygones complexes associés

Les polytopes complexes réguliers ₃ {5} ₃ ,et ₅ {3} ₅ ,, dans avoir une représentation réelle sous forme de 600 cellules dans un espace à 4 dimensions. Les deux ont 120 sommets et 120 arêtes. Le premier a un groupe de réflexion complexe ₃ [5] ₃ , ordre 360, et le second a une symétrie ₅ [3] ₅ , ordre 600. ${\displaystyle \mathbb {C} ^{2}}$

Polytope complexe régulier en projection orthogonale du plan de Coxeter H 4
{3,3,5} Ordre 14400	3 {5} 3 Commande 360	5 {3} 5 Commande 600

Polytopes et nids d'abeilles associés

La cellule 600 est l'un des 15 polytopes réguliers et uniformes de même symétrie [3,3,5] :

Polytopes de la famille H 4
120 cellules	120 cellules rectifiées	120 cellules tronquées	120 cellules cantellées	120 cellules runcinées	120 cellules cantitronnées	tronqué 120-cell	120 cellules omnitronquées
{5,3,3}	r{5,3,3}	t{5,3,3}	rr{5,3,3}	t 0,3 {5,3,3}	tr{5,3,3}	t 0,1,3 {5,3,3}	t 0,1,2,3 {5,3,3}
600 cellules	600 cellules rectifiées	600 cellules tronquées	600 cellules cantellées	600 cellules tronquées	600 cellules cantitronnées	tronqué 600-cell	600 cellules omnitronquées
{3,3,5}	r{3,3,5}	t{3,3,5}	rr{3,3,5}	2t{3,3,5}	tr{3,3,5}	t 0,1,3 {3,3,5}	t 0,1,2,3 {3,3,5}

Il est similaire à trois 4-polytopes réguliers : le 5-cellule {3,3,3}, 16-cell {3,3,4} de l'espace 4 euclidien, et le nid d'abeille tétraédrique d'ordre-6 {3,3, 6} de l'espace hyperbolique. Tous ont des cellules tétraédriques .

{3,3,p} polytopes
Espacer	S 3			H 3
Former	Fini			Paracompacte	Non compact
Nom	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	... {3,3,∞}
Image
Figure de sommet	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Ce 4-polytope fait partie d'une séquence de 4-polytopes et de nids d'abeilles avec des figures de sommet d' icosaèdre :

{p,3,5} polytopes
Espacer	S 3	H 3
Former	Fini	Compact		Paracompacte	Non compact
Nom	{3,3,5}	{4,3,5}	{5,3,5}	{6,3,5}	{7,3,5}	{8,3,5}	... {∞,3,5}
Image
Cellules	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Voir également

• 24-cell , le prédécesseur 4-polytope sur lequel le 600-cell est basé
• 120-cell , le double 4-polytope au 600-cell, et son successeur
• Famille uniforme de 4 polytopes avec symétrie [5,3,3]
• Régulier 4-polytope
• Polytope

Remarques

Citations

Les références

Liens externes

• Weisstein, Eric W. "600 cellules" . MathWorld .
• Olchevski, Georges. "Hexacosichoron" . Glossaire de l'hyperespace . Archivé de l'original le 4 février 2007.
  • Polychore uniforme convexe basé sur l'hécatonicosachore (120 cellules) et l'hexacosichoron (600 cellules) - Modèle 35 , George Olshevsky.
• Klitzing, Richard. "Polytopes uniformes 4D (polychora) x3o3o5o - ex" .
• Der 600-Zeller (600-cell) Polytopes réguliers de Marco Möller dans R ⁴ (allemand)
• L' expansion centrée du 600-Cell Vertex du 600-cell