Critère de Hilbert-Mumford - Hilbert–Mumford criterion

En mathématiques , le critère de Hilbert-Mumford , introduit par David Hilbert et David Mumford , caractérise les points semi -stables et stables d'une action de groupe sur un espace vectoriel en termes de valeurs propres de sous - groupes à 1 paramètre (Dieudonné & Carrell  1970 , 1971 , p. 58).

Définition de la stabilité

Lorsque le poids sur la fibre au-dessus de la limite x ₀ est positif, le point x est ramené à 0 le long de l' action C ^* et la fermeture de l'orbite contient 0 . Lorsque le poids est positif, x tend vers l'infini et l'orbite est fermée.

Soit G un groupe réducteur agissant linéairement sur un espace vectoriel V , un point non nul de V est appelé

• semi-stable si 0 n'est pas contenu dans la fermeture de son orbite, et instable sinon ;
• stable si son orbite est fermée, et son stabilisateur est fini. Un point stable est a fortiori semi-stable. Un point semi-stable mais non stable est dit strictement semi-stable .

Lorsque G est le groupe multiplicatif , par exemple C ^* dans le cadre complexe, l'action équivaut à une représentation de dimension finie . Nous pouvons décomposer V en une somme directe , où sur chaque composante V _i l'action est donnée par . L'entier i est appelé le poids. Ensuite, pour chaque point x , nous regardons l'ensemble des poids dans lequel il a une composante non nulle. ${\displaystyle \mathbb {G} _{m}}$${\displaystyle \lambda \colon \mathbf {C} ^{*}\to \mathrm {GL} (V)}$${\displaystyle V=\textstyle \bigoplus _{i}V_{i}}$${\displaystyle \lambda (t)\cdot v=t^{i}v}$

• Si tous les poids sont strictement positifs, alors , donc 0 est dans la fermeture de l'orbite de x , c'est-à-dire que x est instable ;${\displaystyle \lim _{t\to 0}\lambda (t)\cdot x=0}$
• Si tous les poids sont non négatifs, 0 étant un poids, alors soit 0 est le seul poids, auquel cas x est stabilisé par C ^* ; ou il y a des poids positifs à côté de 0, alors la limite est égale à la composante poids-0 de x , qui n'est pas dans l'orbite de x . Les deux cas correspondent donc exactement à l'échec respectif des deux conditions dans la définition d'un point stable, c'est-à-dire que nous avons montré que x est strictement semi-stable.${\displaystyle \lim _{t\to 0}\lambda (t)\cdot x}$

Déclaration

Le critère de Hilbert-Mumford dit essentiellement que le cas du groupe multiplicatif est la situation typique. Précisément, pour un groupe réducteur général G agissant linéairement sur un espace vectoriel V , la stabilité d'un point x peut être caractérisée via l'étude de sous-groupes à 1 paramètre de G , qui sont des morphismes non triviaux . Notez que les poids de l'inverse sont précisément moins ceux de , de sorte que les déclarations peuvent être rendues symétriques. ${\displaystyle \lambda \colon \mathbb {G} _{m}\to G}$${\displaystyle \lambda ^{-1}}$${\style d'affichage \lambda }$

• Un point x est instable si et seulement s'il existe un sous-groupe à 1 paramètre de G pour lequel x n'admet que des poids positifs ou que des poids négatifs ; de manière équivalente, x est semi-stable si et seulement s'il n'y a pas de tel sous-groupe à 1 paramètre, c'est-à-dire pour chaque sous-groupe à 1 paramètre il y a à la fois des poids non positifs et non négatifs ;
• Un point x est strictement semi-stable si et seulement s'il existe un sous-groupe à 1 paramètre de G pour lequel x admet 0 comme poids, tous les poids étant non négatifs (ou non positifs) ;
• Un point x est stable si et seulement s'il n'y a pas de sous-groupe à 1 paramètre de G pour lequel x n'admet que des poids non négatifs ou que des poids non positifs, c'est-à-dire que pour chaque sous-groupe à 1 paramètre il y a à la fois des poids positifs et négatifs.

Exemples et applications

L'action de C ^* sur le plan C ² , les orbites étant des coniques planes (hyperboles).

Action de C ^* dans l'avion

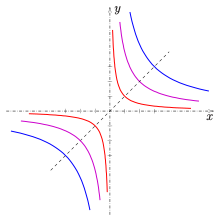
L'exemple type est l'action de C ^* sur le plan C ² défini comme . Il est clair que le poids dans la direction x est 1 et le poids dans la direction y est -1. Ainsi, selon le critère de Hilbert-Mumford, un point non nul sur l' axe des x admet 1 comme seul poids, et un point non nul sur l' axe des y admet -1 comme seul poids, ils sont donc tous les deux instables ; un point général du plan admet à la fois 1 et -1 comme poids, il est donc stable. ${\displaystyle t\cdot (x,y)=(tx,t^{-1}y)}$

Points dans P ¹

De nombreux exemples se présentent dans les problèmes de modules . Par exemple, considérons un ensemble de n points sur la courbe rationnelle P ¹ (plus précisément, un sous-schéma de longueur n de P ¹ ). Le groupe d'automorphismes de P ¹ , PSL(2, C ), agit sur de tels ensembles (sous-schémas), et le critère de Hilbert–Mumford nous permet de déterminer la stabilité sous cette action.

Nous pouvons linéariser le problème en identifiant un ensemble de n points avec un polynôme homogène de degré n à deux variables. On considère donc l'action de SL(2, C ) sur l'espace vectoriel de tels polynômes homogènes. Étant donné un sous-groupe à 1 paramètre , nous pouvons choisir les coordonnées x et y de sorte que l'action sur P ¹ est donnée comme ${\displaystyle H^{0}({\mathcal {O}}_{\mathbf {P} ^{1}}(n))}$${\displaystyle \lambda \colon \mathbf {C} ^{*}\to \mathrm {SL} (2,\mathbf {C} )}$

${\displaystyle \lambda (t)\cdot [x:y]=[t^{k}x:t^{-k}y].}$

Pour un polynôme homogène de forme , le terme a un poids k (2 i - n ). Ainsi le polynôme admet à la fois des poids positifs et négatifs (resp. non positifs et non négatifs) si et seulement s'il existe des termes avec i > n /2 et i < n/2 (resp. i ≥ n /2 et i ≤ n/2 ). En particulier, la multiplicité de x ou y doit être < n /2 (reps. ≤ n /2). Si nous répétons sur tous les sous-groupes à 1 paramètre, nous pouvons obtenir la même condition de multiplicité pour tous les points de P ¹ . Par le critère de Hilbert-Mumford, le polynôme (et donc l'ensemble des n points) est stable (resp. semi-stable) si et seulement si sa multiplicité en tout point est < n /2 (resp. ≤ n /2). ${\displaystyle \textstyle \sum _{i=0}^{n}a_{i}x^{i}y^{ni}}$${\displaystyle x^{i}y^{ni}}$

Cubes d'avion

Une analyse similaire utilisant un polynôme homogène peut être effectuée pour déterminer la stabilité des cubiques planes . Le critère de Hilbert-Mumford montre qu'une cubique plane est stable si et seulement si elle est lisse ; elle est semi-stable si et seulement si elle admet au pire des points doubles ordinaires comme singularités ; un cubique avec des singularités pires (par exemple une cuspide ) est instable.

Voir également

• Théorie des invariants géométriques
• quotient GIT

Les références

• Dieudonné, Jean A. ; Carrell, James B. (1970), "Invariant theory, old and new", Advances in Mathematics , 4 : 1–80, doi : 10.1016/0001-8708(70)90015-0 , ISSN  0001-8708 , MR  0255525
• Dieudonné, Jean A. ; Carrell, James B. (1971), Invariant Theory, Old and New , Boston, MA: Academic Press , ISBN 978-0-12-215540-6, MR  0279102
• Harris, Joe ; Morrison, Ian (1998), Modules de courbes , Springer , doi : 10.1007/b98867
• Thomas, Richard P. (2006), "Notes sur GIT et réduction symplectique pour les fibrés et les variétés", Surveys in Differential Geometry , 10 , arXiv : math/0512411v3