Immersion (mathématiques) - Immersion (mathematics)

La bouteille de Klein , immergée dans 3-space.

En mathématiques , une immersion est une fonction différentiable entre des variétés différentiables dont la dérivée est partout injective . Explicitement, f  : M → N est une immersion si

${\displaystyle D_{p}f:T_{p}M\to T_{f(p)}N\,}$

est une fonction injective en tout point p de M (où T _p X désigne l' espace tangent d'une variété X en un point p de X ). De manière équivalente, f est une immersion si sa dérivée est de rang constant égal à la dimension de M :

${\displaystyle \operatorname {rang} \,D_{p}f=\dim M.}$

La fonction f elle-même n'a pas besoin d'être injective, seule sa dérivée doit l'être.

Un concept connexe est celui d' encastrement . Un plongement lisse est un plongement injectif f  : M → N qui est aussi un plongement topologique , de sorte que M est difféomorphe à son image dans N . Une immersion est précisément un plongement local – c'est-à-dire que pour tout point x ∈ M il existe un voisinage , U ⊆ M , de x tel que f  : U → N est un plongement, et inversement un plongement local est une immersion. Pour les variétés de dimension infinie, cela est parfois considéré comme la définition d'une immersion.

Un sous - variété immergé par injection qui n'est pas un plongement.

Si M est compact , une immersion injective est un plongement, mais si M n'est pas compact, alors les immersions injectives n'ont pas besoin d'être des plongements ; comparer aux bijections continues par rapport aux homéomorphismes .

Homotopie régulière

Une homotopie régulière entre deux immersions f et g d'une variété M dans une variété N est définie comme une fonction différentiable H  : M × [0,1] → N telle que pour tout t dans [0, 1] la fonction H _t  : M → N défini par H _t ( x ) = H ( x , t ) pour tout x ∈ M est une immersion, avec H ₀ = f , H ₁ = g . Une homotopie régulière est donc une homotopie par immersions.

Classification

Hassler Whitney a initié l'étude systématique des immersions et des homotopies régulières dans les années 1940, prouvant que pour 2 m < n + 1 chaque application f  : M ^m → N ⁿ d'une variété de dimension m à une variété de dimension n est homotope à une immersion , et en fait à un plongement pour 2 m < n ; ce sont le théorème d'immersion de Whitney et le théorème de plongement de Whitney .

Stephen Smale a exprimé les classes d'homotopie régulières des immersions f  : M ^m → R ⁿ comme les groupes d'homotopie d'une certaine variété de Stiefel . L' éversion de la sphère en fut une conséquence particulièrement frappante.

Morris Hirsch a généralisé l'expression de Smale à une description de la théorie de l'homotopie des classes d'homotopie régulières des immersions de toute variété à m dimensions M ^m dans toute variété à n dimensions N ⁿ .

La classification Hirsch-Smale des immersions a été généralisée par Mikhail Gromov .

Existence

La bande de Möbius ne plonge pas dans la codimension 0 car son fibré tangent est non trivial.

Le principal obstacle à l'existence d'une immersion i  : M ^m → R ⁿ est le fibré normal stable de M , tel que détecté par ses classes caractéristiques , notamment ses classes de Stiefel–Whitney . Autrement dit, puisque R ⁿ est parallélisable , le retrait de son fibré tangent à M est trivial ; étant donné que ce repli est la somme directe du faisceau de tangente (intrinsèquement défini) sur M , TM , qui est de dimension m , et du faisceau normale ν de l'immersion i , qui est de dimension n - m , pour qu'il y ait un codimension k immersion de M , il doit y avoir un paquet vectoriel de dimension k , ξ ^k , debout normale pour le faisceau ν , de telle sorte que TM ⊕ ξ ^k est triviale. Inversement, étant donné un tel fibré, une immersion de M avec ce fibré normal équivaut à une immersion de codimension 0 de l'espace total de ce fibré, qui est une variété ouverte.

Le fibré normal stable est la classe des fibrés normaux plus fibrés triviaux, et donc si le fibré normal stable a une dimension cohomologique k , il ne peut pas provenir d'un fibré normal (instable) de dimension inférieure à k . Ainsi, la dimension de cohomologie du faisceau normal stable, telle que détectée par sa classe caractéristique non nulle la plus élevée, est une obstruction aux immersions.

Puisque les classes caractéristiques se multiplient sous la somme directe des fibrés vectoriels, cette obstruction peut être énoncée intrinsèquement en termes d'espace M et de son fibré tangent et d'algèbre de cohomologie. Cette obstruction a été indiquée (en termes de fibré tangent, fibré normal non stable) par Whitney.

Par exemple, la bande de Möbius a un fibré tangent non trivial, elle ne peut donc pas s'immerger dans la codimension 0 (dans R ² ), bien qu'elle s'enfonce dans la codimension 1 (dans R ³ ).

William S. Massey  ( 1960 ) a montré que ces classes caractéristiques (les classes Stiefel-Whitney de l'écurie fibré normal) disparaissent degré au- dessus n - α ( n ) , où α ( n ) est le nombre de "1" chiffres lorsque n est écrit en binaire; cette borne est nette, comme le réalise l'espace projectif réel . Cela a donné des preuves à l' immersion Conjecture , à savoir que tous les n -manifold pourrait être immergé dans codimension n - α ( n ) , par exemple, en R ^{2 n -α ( n )} . Cette conjecture a été prouvée par Ralph Cohen  ( 1985 ).

Codimension 0

Les immersions de codimension 0 sont équivalentes à des submersions de dimension 0 relatives et sont mieux considérées comme des submersions. Une immersion de codimension 0 d'une variété fermée est précisément une carte de recouvrement , c'est-à-dire un faisceau de fibres avec une fibre de 0 dimension (discrète). D'après le théorème d'Ehresmann et le théorème de Phillips sur les submersions, une submersion propre de variétés est un fibré de fibres, donc les immersions/submersions de codimension/dimension relative 0 se comportent comme des submersions.

De plus, les immersions de codimension 0 ne se comportent pas comme les autres immersions, qui sont largement déterminées par le fibré normal stable : dans la codimension 0, on a des problèmes de classe fondamentale et d'espaces de couverture. Par exemple, il n'y a pas de codimension 0 immersion S ¹ → R ¹ , bien que le cercle soit parallélisable, ce qui peut être prouvé car la ligne n'a pas de classe fondamentale, donc on n'obtient pas l'application requise sur la cohomologie supérieure. Alternativement, c'est par invariance de domaine . De même, bien que S ³ et le 3-tore T ³ soient tous deux parallélisables, il n'y a pas d'immersion T ³ → S ³ – une telle couverture devrait être ramifiée en certains points, puisque la sphère est simplement connectée.

Une autre façon de comprendre cela est qu'une immersion de codimension k d'une variété correspond à une immersion de codimension 0 d'un fibré vectoriel de dimension k , qui est une variété ouverte si la codimension est supérieure à 0, mais à une variété fermée de codimension 0 ( si le collecteur d'origine est fermé).

Points multiples

A k points uplet (double, triple, etc.) d'une immersion f  : M → N est un ensemble non ordonné { x ₁ , ..., x _k } de points distincts x _i ∈ M avec la même image f ( x _i ) N . Si M est une variété à m dimensions et N est une variété à n dimensions alors pour une immersion f  : M → N en position générale l'ensemble des points k -uplets est une variété ( n − k ( n − m )) à dimensions . Chaque plongement est une immersion sans points multiples (où k > 1 ). Notons cependant que l'inverse est faux : il existe des immersions injectives qui ne sont pas des plongements.

La nature des points multiples classe les immersions ; par exemple, les immersions d'un cercle dans le plan sont classées jusqu'à homotopie régulière par le nombre de points doubles.

À un point clé de la théorie chirurgicale, il est nécessaire de décider si une immersion f  : S ^m → N ^{2 m} d'une m -sphère dans une variété de dimension 2 m est régulière homotope à un plongement, auquel cas elle peut être tuée par opération. Paroi associée à f un invariant μ ( f ) dans un quotient du groupe fondamental anneau Z [ π ₁ ( N )] qui compte les points doubles de f dans le revêtement universel de N . Pour m > 2 , f est régulièrement homotope à un plongement si et seulement si μ ( f ) = 0 par l' astuce de Whitney .

On peut étudier les plongements comme des « immersions sans points multiples », puisque les immersions sont plus faciles à classer. Ainsi, on peut partir d'immersions et essayer d'éliminer des points multiples, voir si on peut le faire sans introduire d'autres singularités – étudier les « disjonctions multiples ». Cela a d'abord été fait par André Haefliger , et cette approche est fructueuse dans la codimension 3 ou plus - du point de vue de la théorie de la chirurgie, c'est "haute (co)dimension", contrairement à la codimension 2 qui est la dimension de nouage, comme dans le nœud théorie . Elle est étudiée de manière catégorique via le « calcul des foncteurs » par Thomas Goodwillie , John Klein et Michael S. Weiss .

Exemples et propriétés

Le quadrifolium , la rose à 4 pétales.

• Une rose mathématique avec k pétales est une immersion du cercle dans le plan avec un seul point k -uplet ; k peut être n'importe quel nombre impair, mais si pair doit être un multiple de 4, le chiffre 8 n'est donc pas une rose.
• La bouteille de Klein , et toutes les autres surfaces fermées non orientables, peuvent être immergées dans 3 espaces mais non encastrées.
• Par le théorème de Whitney-Graustein , les classes d'homotopie régulières d'immersions du cercle dans le plan sont classées par le nombre d'enroulement , qui est aussi le nombre de points doubles comptés algébriquement (c'est-à-dire avec des signes).
• La sphère peut être retournée : le plongement standard f ₀  : S ² → R ³ est lié à f ₁ = − f ₀  : S ² → R ³ par une homotopie régulière des immersions f _t  : S ² → R ³ .
• La surface de Boy est une immersion du plan projectif réel dans l'espace 3 ; donc aussi une immersion 2 à 1 de la sphère.
• La surface de Morin est une immersion de la sphère ; à la fois elle et la surface de Boy apparaissent comme des modèles intermédiaires dans l'éversion de la sphère.

• 

  Surface garçon

• 

  La surface de Morin

Courbes planes immergées

Cette courbe a une courbure totale  6 π , et le numéro tournant  3, même si elle n'a enroulement numéro  2 environ  p .

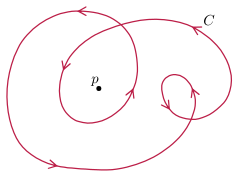
Courbes planes immergées ont un bien défini numéro tournant , qui peut être définie comme étant la courbure totale divisée par 2 π . Ceci est invariant sous homotopie régulière, par le théorème de Whitney-Graustein - topologiquement, c'est le degré de l'application de Gauss , ou de manière équivalente le nombre d'enroulement de l'unité tangente (qui ne s'annule pas) autour de l'origine. De plus, il s'agit d'un ensemble complet d'invariants - deux courbes planes avec le même nombre de virages sont homotopes réguliers.

Chaque courbe plane immergée s'élève vers une courbe spatiale incorporée en séparant les points d'intersection, ce qui n'est pas vrai dans les dimensions supérieures. Avec des données supplémentaires (quel brin est au-dessus), les courbes planes immergées donnent des diagrammes de nœuds , qui sont d'un intérêt central dans la théorie des nœuds . Alors que les courbes planes immergées, jusqu'à homotopie régulière, sont déterminées par leur nombre de tours, les nœuds ont une structure très riche et complexe.

Surfaces immergées dans 3 espaces

L'étude des surfaces immergées dans l'espace 3 est étroitement liée à l'étude des surfaces nouées (encastrées) dans l'espace 4, par analogie avec la théorie des diagrammes de nœuds (courbes planes immergées (espace 2) comme projections de courbes nouées dans l'espace 3 -espace) : étant donné une surface nouée en 4-espace, on peut la projeter sur une surface immergée en 3-espace, et inversement, étant donné une surface immergée en 3-espace, on peut se demander si elle s'élève en 4-espace - est est-ce la projection d'une surface nouée dans l'espace 4 ? Cela permet de relier les questions sur ces objets.

Un résultat de base, contrairement au cas des courbes planes, est que toutes les surfaces immergées ne se soulèvent pas jusqu'à une surface nouée. Dans certains cas, l'obstruction est à 2 torsion, comme dans l'exemple de Koschorke , qui est une surface immergée (formée de 3 bandes de Möbius, avec un point triple ) qui ne se soulève pas jusqu'à une surface nouée, mais elle a une double couverture qui ne ascenseur. Une analyse détaillée est donnée dans Carter & Saito (1998a) , tandis qu'une enquête plus récente est donnée dans Carter, Kamada & Saito (2004) .

Généralisations

Une généralisation de grande envergure de la théorie de l'immersion est le principe d'homotopie : on peut considérer la condition d'immersion (le rang de la dérivée est toujours k ) comme une relation aux dérivées partielles (PDR), car elle peut être énoncée en termes de dérivées partielles de la fonction. Ensuite, la théorie de l'immersion Smale-Hirsch est le résultat que cela se réduit à la théorie de l'homotopie, et le principe de l'homotopie donne des conditions générales et des raisons pour que les PDR se réduisent à la théorie de l'homotopie.

Voir également

• Sous-collecteur immergé
• Immersion isométrique
• Submersion

Remarques

Les références

Liens externes

• Immersion au Manifold Atlas
• Immersion d'une variété à l'Encyclopédie des mathématiques