Polynôme de Lagrange - Lagrange polynomial

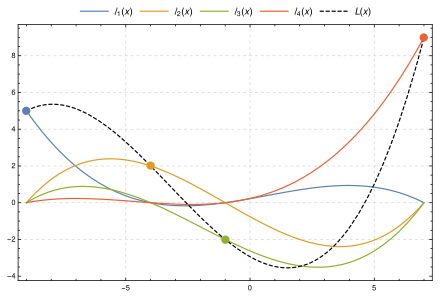
Cette image montre, pour quatre points ( (−9, 5) , (−4, 2) , (−1, −2) , (7, 9) ), le polynôme d'interpolation (cubique) L ( x ) (en pointillés, noir), qui est la somme des mises à l' échelle polynômes de base y ₀ ℓ ₀ ( x ) , y ₁ ℓ ₁ ( x ) , y ₂ ℓ ₂ ( x ) et y ₃ ℓ ₃ ( x ) . Le polynôme d'interpolation passe par les quatre points de contrôle, et chaque polynôme de base mis à l' échelle passe par son point de contrôle respectif et vaut 0 où x correspond aux trois autres points de contrôle.

En analyse numérique , les polynômes de Lagrange sont utilisés pour l' interpolation polynomiale . Pour un ensemble donné de points sans deux valeurs égales, le polynôme de Lagrange est le polynôme de degré le plus bas qui prend à chaque valeur la valeur correspondante , de sorte que les fonctions coïncident en chaque point. ${\style d'affichage (x_{j},y_{j})}$${\style d'affichage x_{j}}$${\style d'affichage x_{j}}$${\style d'affichage y_{j}}$

Bien que nommée d'après Joseph-Louis Lagrange , qui l'a publiée en 1795, la méthode a été découverte pour la première fois en 1779 par Edward Waring . C'est aussi une conséquence facile d'une formule publiée en 1783 par Leonhard Euler .

Les utilisations des polynômes de Lagrange incluent la méthode d' intégration numérique de Newton-Cotes et le schéma de partage secret de Shamir en cryptographie .

L'interpolation de Lagrange est sensible au phénomène de grande oscillation de Runge . Comme changer les points nécessite de recalculer l'intégralité de l'interpolant, il est souvent plus facile d'utiliser des polynômes de Newton à la place. ${\style d'affichage x_{j}}$

Définition

Ici, nous traçons les fonctions de base de Lagrange de 1er, 2e et 3e ordre sur un domaine bi-unitaire. Des combinaisons linéaires de fonctions de base de Lagrange sont utilisées pour construire des polynômes d'interpolation de Lagrange. Les fonctions de base de Lagrange sont couramment utilisées dans l' analyse par éléments finis comme bases pour les fonctions de forme des éléments. De plus, il est courant d'utiliser un domaine bi-unitaire comme espace naturel pour la définition des éléments finis.

Étant donné un ensemble de k  + 1 points de données

${\displaystyle (x_{0},y_{0}),\ldots ,(x_{j},y_{j}),\ldots ,(x_{k},y_{k})}$

où il n'y en a pas deux , le polynôme d'interpolation sous la forme de Lagrange est une combinaison linéaire${\style d'affichage x_{j}}$

${\displaystyle L(x):=\sum _{j=0}^{k}y_{j}\ell _{j}(x)}$

des polynômes de base de Lagrange

${\displaystyle \ell _{j}(x):=\prod _{\begin{smallmatrix}0\leq m\leq k\\m\neq j\end{smallmatrix}}{\frac {x-x_{ m}}{x_{j}-x_{m}}}={\frac {(x-x_{0})}{(x_{j}-x_{0})}}\cdots {\frac {( x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{ j+1})}}\cdots {\frac {(x-x_{k})}{(x_{j}-x_{k})}},}$

où . Notez comment, étant donné l'hypothèse initiale selon laquelle il n'y en a pas deux identiques, alors (quand ) , cette expression est donc toujours bien définie. Les paires de motif avec ne sont pas autorisés est qu'aucune fonction d'interpolation de telle sorte que existerait; une fonction ne peut obtenir qu'une seule valeur pour chaque argument . D'un autre côté, si aussi , alors ces deux points seraient en fait un seul point. ${\style d'affichage 0\leq j\leq k}$${\style d'affichage x_{j}}$${\style d'affichage m\neq j}$${\style d'affichage x_{j}-x_{m}\neq 0}$${\style d'affichage x_{i}=x_{j}}$${\displaystyle y_{i}\neq y_{j}}$${\style d'affichage L}$${\displaystyle y_{i}=L(x_{i})}$${\style d'affichage x_{i}}$${\displaystyle y_{i}=y_{j}}$

Pour tout , inclut le terme dans le numérateur, donc le produit entier sera égal à zéro à : ${\style d'affichage i\neq j}$${\displaystyle \ell _{j}(x)}$${\style d'affichage (x-x_{i})}$${\style d'affichage x=x_{i}}$

${\displaystyle \forall ({j\neq i}):\ell _{j}(x_{i})=\prod _{m\neq j}{\frac {x_{i}-x_{m}} {x_{j}-x_{m}}}={\frac {(x_{i}-x_{0})}{(x_{j}-x_{0})}}}\cdots {\frac {( x_{i}-x_{i})}{(x_{j}-x_{i})}}\cdots {\frac {(x_{i}-x_{k})}{(x_{j}- x_{k})}}=0.}$

D'autre part,

$${\displaystyle \ell _{j}(x_{j}):=\prod _{m\neq j}{\frac {x_{j}-x_{m}}{x_{j}-x_{m} }}=1}$$

En d'autres termes, tous les polynômes de base sont nuls à , à l'exception de , pour lequel il maintient que , car il manque le terme. ${\style d'affichage x=x_{j}}$${\displaystyle \ell _{j}(x)}$${\displaystyle \ell _{j}(x_{j})=1}$${\style d'affichage (x-x_{j})}$

Il s'ensuit que , donc à chaque point , , montrant qu'interpole exactement la fonction. ${\displaystyle y_{j}\ell _{j}(x_{j})=y_{j}}$${\style d'affichage x_{j}}$${\displaystyle L(x_{j})=y_{j}+0+0+\dots +0=y_{j}}$${\style d'affichage L}$

Preuve

La fonction L ( x ) recherchée est un polynôme en x du moindre degré qui interpole l'ensemble de données donné ; c'est-à-dire qu'il prend la valeur y _j au x _j correspondant pour tous les points de données j :

${\displaystyle L(x_{j})=y_{j}\qquad j=0,\ldots ,k.}$

Observe ceci:

• Il y a k facteurs dans le produit et chaque facteur contient un x , donc L ( x ) (qui est la somme de ces polynômes de k degrés) doit être un polynôme de degré au plus k .${\displaystyle \ell _{j}(x)}$
• ${\displaystyle \ell _{j}(x_{i})=\prod _{\begin{smallmatrix}m=0\\m\neq j\end{smallmatrix}}^{k}{\frac {x_{ i}-x_{m}}{x_{j}-x_{m}}}.}$

Développez ce produit. Puisque le produit omet le terme où m = j , si i = j alors tous les termes qui apparaissent sont . En outre, si i ≠ j puis une durée dans le produit sera soit (pour m = i ), la réduction à zéro la totalité du produit. Donc, ${\style d'affichage {\frac {x_{j}-x_{m}}{x_{j}-x_{m}}}=1}$${\style d'affichage {\frac {x_{i}-x_{i}}{x_{j}-x_{i}}}=0}$

${\displaystyle \ell _{j}(x_{i})=\delta _{ji}={\begin{cases}1,&{\text{if }}j=i\\0,&{\text {if }}j\neq i\end{cas}},}$

où est le delta de Kronecker . Donc: ${\displaystyle \delta _{ij}}$

${\displaystyle L(x_{i})=\sum _{j=0}^{k}y_{j}\ell _{j}(x_{i})=\sum _{j=0}^{ k}y_{j}\delta _{ji}=y_{i}.}$

Ainsi la fonction L ( x ) est un polynôme de degré au plus k et où L ( x _i ) = y _i .

De plus, le polynôme d'interpolation est unique, comme le montre le théorème d'unisolvence à l' article d' interpolation polynomiale .

C'est vrai aussi que :

${\displaystyle \sum _{j=0}^{k}\ell _{j}(x)=1\qquad \forall x}$

puisqu'il doit être un polynôme de degré, au plus, k et passe par tous ces k  + 1 points de données :

${\style d'affichage (x_{0},1),\ldots ,(x_{j},1),\ldots ,(x_{k},1)}$

résultant en une ligne horizontale, puisqu'une ligne droite est le seul polynôme de degré inférieur à k  + 1 qui passe par k  + 1 points alignés.

Une perspective de l'algèbre linéaire

La résolution d'un problème d'interpolation conduit à un problème d'algèbre linéaire équivalent à l'inversion d'une matrice. En utilisant une base de monôme standard pour notre polynôme d'interpolation , nous devons inverser la matrice de Vandermonde pour résoudre les coefficients de . En choisissant une meilleure base, la base de Lagrange, , on obtient simplement la matrice identité , , qui est son propre inverse : la base de Lagrange inverse automatiquement l'analogue de la matrice de Vandermonde. ${\textstyle L(x)=\sum _{j=0}^{k}x^{j}m_{j}}$ ${\style d'affichage (x_{i})^{j}}$${\style d'affichage L(x_{i})=y_{i}}$${\style d'affichage m_{j}}$${\style d'affichage L(x)}$${\textstyle L(x)=\sum _{j=0}^{k}l_{j}(x)y_{j}}$${\displaystyle \delta _{ij}}$

Cette construction est analogue au théorème des restes chinois . Au lieu de vérifier les restes des nombres entiers modulo premiers, nous vérifions les restes des polynômes lorsqu'ils sont divisés par des linéaires.

De plus, lorsque l'ordre est grand, la transformation de Fourier rapide peut être utilisée pour résoudre les coefficients du polynôme interpolé.

Exemples

Exemple 1

On souhaite interpoler ƒ ( x ) =  x ² sur l'intervalle 1 ≤  x  ≤ 3, étant donné ces trois points :

${\displaystyle {\begin{aligned}x_{0}&=1&&&f(x_{0})&=1\\x_{1}&=2&&&f(x_{1})&=4\\x_{2}& =3&&&f(x_{2})&=9.\end{aligned}}}$

Le polynôme d'interpolation est :

${\displaystyle {\begin{aligned}L(x)&={1}\cdot {x-2 \over 1-2}\cdot {x-3 \over 1-3}+{4}\cdot {x -1 \over 2-1}\cdot {x-3 \over 2-3}+{9}\cdot {x-1 \over 3-1}\cdot {x-2 \over 3-2}\\ [10pt]&=x^{2}.\end{aligned}}}$

Exemple 2

On souhaite interpoler ƒ ( x ) =  x ³ sur l'intervalle 1 ≤  x  ≤ 4, étant donné ces quatre points :

${\style d'affichage x_{0}=1}$	${\style d'affichage f(x_{0})=1}$
${\style d'affichage x_{1}=2}$	${\style d'affichage f(x_{1})=8}$
${\style d'affichage x_{2}=3}$	${\style d'affichage f(x_{2})=27}$
${\style d'affichage x_{3}=4}$	${\style d'affichage f(x_{3})=64}$

Le polynôme d'interpolation est :

${\displaystyle {\begin{aligned}L(x)&={1}\cdot {x-2 \over 1-2}\cdot {x-3 \over 1-3}\cdot {x-4 \over 1-4}+{8}\cdot {x-1 \over 2-1}\cdot {x-3 \over 2-3}\cdot {x-4 \over 2-4}+{27}\cdot {x-1 \over 3-1}\cdot {x-2 \over 3-2}\cdot {x-4 \over 3-4}+{64}\cdot {x-1 \over 4-1} \cdot {x-2 \over 4-2}\cdot {x-3 \over 4-3}\\[8pt]&=x^{3}\end{aligned}}}$

Remarques

Exemple de divergence d'interpolation pour un ensemble de polynômes de Lagrange.

La forme de Lagrange du polynôme d'interpolation montre le caractère linéaire de l'interpolation polynomiale et l'unicité du polynôme d'interpolation. Par conséquent, il est préféré dans les preuves et les arguments théoriques. L'unicité peut également être vue à partir de l'inversibilité de la matrice de Vandermonde, due à la non-annulation du déterminant de Vandermonde .

Mais, comme le montre la construction, chaque fois qu'un nœud x _k change, tous les polynômes de base de Lagrange doivent être recalculés. Une meilleure forme du polynôme d'interpolation à des fins pratiques (ou de calcul) est la forme barycentrique de l'interpolation de Lagrange (voir ci-dessous) ou des polynômes de Newton .

Lagrange et d'autres interpolations à des points également espacés, comme dans l'exemple ci-dessus, produisent un polynôme oscillant au-dessus et au-dessous de la vraie fonction. Ce comportement a tendance à croître avec le nombre de points, conduisant à une divergence connue sous le nom de phénomène de Runge ; le problème peut être éliminé en choisissant des points d'interpolation aux nœuds de Chebyshev .

Les polynômes de base de Lagrange peuvent être utilisés en intégration numérique pour dériver les formules de Newton-Cotes .

Forme barycentrique

À l'aide de

${\displaystyle \ell (x)=(x-x_{0})(x-x_{1})\cdots (x-x_{k})}$

${\displaystyle \ell '(x_{j})={\frac {\mathrm {d} \ell (x)}{\mathrm {d} x}}{\Big |}_{x=x_{j} }=\prod _{i=0,i\neq j}^{k}(x_{j}-x_{i})}$

nous pouvons réécrire les polynômes de base de Lagrange comme

${\displaystyle \ell _{j}(x)={\frac {\ell (x)}{\ell '(x_{j})(x-x_{j})}}}$

ou, en définissant les poids barycentriques

${\displaystyle w_{j}={\frac {1}{\ell '(x_{j})}}}$

on peut simplement écrire

${\displaystyle \ell _{j}(x)=\ell (x){\frac {w_{j}}{x-x_{j}}}}$

qui est communément appelée la première forme de la formule d'interpolation barycentrique.

L'avantage de cette représentation est que le polynôme d'interpolation peut maintenant être évalué comme

${\displaystyle L(x)=\ell (x)\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}y_{j}}$

qui, si les poids ont été pré-calculés, ne nécessite que des opérations (l'évaluation et les poids ) par opposition à l' évaluation individuelle des polynômes de base de Lagrange . ${\style d'affichage w_{j}}$${\displaystyle {\mathcal {O}}(k)}$${\style d'affichage \ell (x)}$${\style d'affichage w_{j}/(x-x_{j})}$${\displaystyle {\mathcal {O}}(k^{2})}$${\displaystyle \ell _{j}(x)}$

La formule d'interpolation barycentrique peut également être facilement mise à jour pour incorporer un nouveau nœud en divisant chacun des , par et en construisant le nouveau comme ci-dessus. ${\style d'affichage x_{k+1}}$${\style d'affichage w_{j}}$${\displaystyle j=0\dots k}$${\style d'affichage (x_{j}-x_{k+1})}$${\displaystyle w_{k+1}}$

On peut encore simplifier la première forme en considérant d'abord l'interpolation barycentrique de la fonction constante : ${\style d'affichage g(x)\équiv 1}$

${\displaystyle g(x)=\ell (x)\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}.}$

La division par ne modifie pas l'interpolation, mais donne ${\style d'affichage L(x)}$${\style d'affichage g(x)}$

${\displaystyle L(x)={\frac {\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}y_{j}}{\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}}}}$

qui est appelée la deuxième forme ou forme vraie de la formule d'interpolation barycentrique. Cette seconde forme a l'avantage de ne pas avoir besoin d'être évaluée pour chaque évaluation de . ${\style d'affichage \ell (x)}$${\style d'affichage L(x)}$

Reste dans la formule d'interpolation de Lagrange

En interpolant une fonction donnée f par un polynôme de degré k aux nœuds, nous obtenons le reste qui peut être exprimé sous la forme ${\style d'affichage x_{0},...,x_{k}}$${\style d'affichage R(x)=f(x)-L(x)}$

${\displaystyle R(x)=f[x_{0},\ldots ,x_{k},x]\ell (x)=\ell (x){\frac {f^{(k+1)}( \xi )}{(k+1)!}},\quad \quad x_{0}<\xi <x_{k},}$

où est la notation pour les différences divisées . Alternativement, le reste peut être exprimé comme une intégrale de contour dans le domaine complexe comme ${\displaystyle f[x_{0},\ldots ,x_{k},x]}$

${\displaystyle R(x)={\frac {\ell (x)}{2\pi i}}\int _{C}{\frac {f(t)}{(tx)(t-x_{0 })\cdots (t-x_{k})}}dt={\frac {\ell (x)}{2\pi i}}\int _{C}{\frac {f(t)}{( tx)\ell (t)}}dt.}$

Le reste peut être lié comme

${\displaystyle |R(x)|\leq {\frac {(x_{k}-x_{0})^{k+1}}{(k+1)!}}\max _{x_{0} \leq \xi \leq x_{k}}|f^{(k+1)}(\xi )|.}$

Dérivation

De toute évidence, est zéro aux nœuds. Pour trouver en un point , définissez une nouvelle fonction et choisissez où est la constante que nous devons déterminer pour un donné . Nous choisissons de telle sorte qu'il y ait des zéros (à tous les nœuds et ) entre et (y compris les extrémités). En supposant que est -Times différentiables, depuis et sont polynômes, et donc, sont infiniment différentiables, sera -Times différentiables. Par le théorème de Rolle , a des zéros, a des zéros... a 1 zéro, disons . Ecrit explicitement : ${\style d'affichage R(x)}$${\style d'affichage R(x)}$${\style d'affichage x_{p}}$${\displaystyle F(x)=R(x)-{\tilde {R}}(x)=f(x)-L(x)-{\tilde {R}}(x)}$${\textstyle {\tilde {R}}(x)=C\cdot \prod _{i=0}^{k}(x-x_{i})}$${\style d'affichage C}$${\style d'affichage x_{p}}$${\style d'affichage C}$${\style d'affichage F(x)}$${\style d'affichage k+2}$${\style d'affichage x_{p}}$${\style d'affichage x_{0}}$${\style d'affichage x_{k}}$${\style d'affichage f(x)}$${\style d'affichage k+1}$${\style d'affichage L(x)}$${\style d'affichage {\tilde {R}}(x)}$${\style d'affichage F(x)}$${\style d'affichage k+1}$${\style d'affichage F^{(1)}(x)}$${\style d'affichage k+1}$${\style d'affichage F^{(2)}(x)}$${\style d'affichage k}$${\style d'affichage F^{(k+1)}}$${\displaystyle \xi ,\,x_{0}<\xi <x_{k}}$${\style d'affichage F^{(k+1)}(\xi )}$

${\displaystyle F^{(k+1)}(\xi )=f^{(k+1)}(\xi )-L^{(k+1)}(\xi )-{\tilde {R }}^{(k+1)}(\xi )}$

${\displaystyle L^{(k+1)}=0,{\tilde {R}}^{(k+1)}=C\cdot (k+1) !}$(Parce que la puissance la plus élevée de in est )${\style d'affichage x}$${\style d'affichage {\tilde {R}}(x)}$${\style d'affichage k+1}$

${\displaystyle 0=f^{(k+1)}(\xi )-C\cdot (k+1) !}$

L'équation peut être réarrangée comme

${\displaystyle C={\frac {f^{(k+1)}(\xi )}{(k+1)!}}}$

Puisque nous avons${\style d'affichage F(x_{p})=0}$${\displaystyle R(x_{p})={\tilde {R}}(x_{p})={\frac {f^{k+1}(\xi )}{(k+1)!}} \prod _{i=0}^{k}(x_{p}-x_{i})}$

Dérivés

Les dérivées e du polynôme de Lagrange peuvent s'écrire sous la forme ${\style d'affichage d}$

${\displaystyle L^{(d)}(x):=\sum _{j=0}^{k}y_{j}\ell _{j}^{(d)}(x)}$.

Pour la dérivée première, les coefficients sont donnés par

${\displaystyle \ell _{j}^{(1)}(x):=\sum _{\begin{smallmatrix}i=0\\i\not =j\end{smallmatrix}}}^{k}\ gauche[{\frac {1}{x_{j}-x_{i}}}\prod _{\begin{smallmatrix}m=0\\m\not =(i,j)\end{smallmatrix}}^ {k}{\frac {x-x_{m}}{x_{j}-x_{m}}}\right]}$

et pour la dérivée seconde

${\displaystyle \ell _{j}^{(2)}(x):=\sum _{\begin{smallmatrix}i=0\\i\neq j\end{smallmatrix}}}^{k}{\ frac {1}{x_{j}-x_{i}}}\left[\sum _{\begin{smallmatrix}m=0\\m\neq (i,j)\end{smallmatrix}}^{k }\left({\frac {1}{x_{j}-x_{m}}}\prod _{\begin{smallmatrix}l=0\\l\neq (i,j,m)\end{smallmatrix }}^{k}{\frac {x-x_{l}}{x_{j}-x_{l}}}\right)\right]}$.

Grâce à la récursivité, on peut calculer des formules pour les dérivées supérieures.

Champs finis

Le polynôme de Lagrange peut également être calculé dans des corps finis . Cela a des applications en cryptographie , comme dans le schéma de partage secret de Shamir .

Voir également

• L'algorithme de Neville
• Forme de Newton du polynôme d'interpolation
• polynôme de Bernstein
• Le théorème de Carlson
• Constante de Lebesgue (interpolation)
• Le système Chebfun
• Tableau des séries newtoniennes
• covariante de Frobenius
• La formule de Sylvestre
• Coefficient de différence finie

Les références

Liens externes

• "Formule d'interpolation de Lagrange" , Encyclopédie des mathématiques , EMS Press , 2001 [1994]
• ALGLIB a une implémentation en C++ / C# / VBA / Pascal.
• GSL a un code d'interpolation polynomiale en C
• SO a un exemple MATLAB qui démontre l'algorithme et recrée la première image de cet article
• Méthode d'interpolation de Lagrange — Notes, PPT, Mathcad, Mathematica, MATLAB, Maple au Holistic Numerical Methods Institute
• Polynôme d'interpolation de Lagrange sur www.math-linux.com
• Weisstein, Eric W. "Lagrange Interpolating Polynôme" . MathWorld .
• Polynôme de Lagrange sur ProofWiki
• Interpolation de Lagrange dynamique avec JSXGraph
• Calcul numérique avec fonctions : le projet Chebfun
• Fonction de feuille de calcul Excel pour l'interpolation de Lagrange bicubique
• Polynômes de Lagrange en Python