Théorème de Rolle - Rolle's theorem

Si une fonction réelle

f

est continue sur un intervalle fermé

[a, b]

, différentiable sur l' intervalle ouvert

(a, b)

, et

f (a) = f (b)

, alors il existe un

c

dans l'intervalle ouvert

(a, b)

tel que

f (c) = 0

.

En calcul , le théorème de Rolle ou le lemme de Rolle stipule essentiellement que toute fonction différentiable à valeur réelle qui atteint des valeurs égales en deux points distincts doit avoir au moins un point stationnaire quelque part entre eux, c'est-à-dire un point où la dérivée première (la pente de la tangente au graphique de la fonction) est nul. Le théorème porte le nom de Michel Rolle .

Version standard du théorème

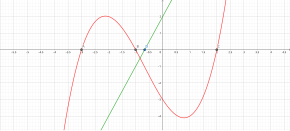
Si une fonction réelle $f$ est continue sur un intervalle fermé propre $[a, b]$ , différentiable sur l' intervalle ouvert $(a, b)$ , et $f (a) = f (b)$ , alors il existe au moins un $c$ dans l'intervalle ouvert $(a, b)$ tel que

{\style d'affichage f'(c)=0}

.

Cette version du théorème de Rolle est utilisée pour prouver le théorème de la valeur moyenne , dont le théorème de Rolle est en effet un cas particulier. C'est aussi la base de la preuve du théorème de Taylor .

Histoire

Bien que le théorème porte le nom de Michel Rolle , la preuve de Rolle de 1691 ne couvrait que le cas des fonctions polynomiales. Sa preuve n'a pas utilisé les méthodes du calcul différentiel , qu'à ce moment de sa vie il considérait comme fallacieuses. Le théorème a été prouvé pour la première fois par Cauchy en 1823 comme corollaire d'une preuve du théorème de la valeur moyenne . Le nom "théorème de Rolle" a été utilisé pour la première fois par Moritz Wilhelm Drobisch d'Allemagne en 1834 et par Giusto Bellavitis d'Italie en 1846.

Exemples

Premier exemple

Un demi - cercle de rayon

r

.

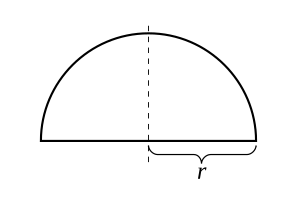
Pour un rayon $r > 0$ , considérons la fonction

f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r].

Son graphe est le demi-cercle supérieur centré à l'origine. Cette fonction est continue sur l'intervalle fermé $[- r, r]$ et dérivable dans l'intervalle ouvert $(- r, r)$ , mais non dérivable aux extrémités $- r$ et $r$ . Puisque $f (- r) = f (r)$ , le théorème de Rolle s'applique, et en effet, il existe un point où la dérivée de $f$ est nulle. Notez que le théorème s'applique même lorsque la fonction ne peut pas être différenciée aux extrémités, car il nécessite uniquement que la fonction soit différentiable dans l'intervalle ouvert.

Deuxième exemple

Le graphique de la fonction valeur absolue.

Si la différentiabilité échoue en un point intérieur de l'intervalle, la conclusion du théorème de Rolle peut ne pas tenir. Considérons la fonction valeur absolue

f(x)=|x|,\qquad x\in [-1,1].

Alors $f (-1) = f (1)$ , mais il n'y a pas de $c$ entre −1 et 1 pour lequel le $f (c)$ est nul. En effet, cette fonction, bien que continue, n'est pas dérivable en $x = 0$ . Notez que la dérivée de $f$ change de signe à $x = 0$ , mais sans atteindre la valeur 0. Le théorème ne peut pas être appliqué à cette fonction car il ne satisfait pas la condition que la fonction doit être dérivable pour chaque $x$ dans l'intervalle ouvert. Cependant, lorsque l'exigence de différentiabilité est supprimée du théorème de Rolle, $f$ aura toujours un nombre critique dans l'intervalle ouvert $(a, b)$ , mais il peut ne pas produire de tangente horizontale (comme dans le cas de la valeur absolue représentée dans le graphique ).

Généralisation

Le deuxième exemple illustre la généralisation suivante du théorème de Rolle :

Considérons une fonction continue à valeur réelle $f$ sur un intervalle fermé $[a, b]$ avec $f (a) = f (b)$ . Si pour chaque $x$ dans l'intervalle ouvert $(a, b)$ la limite de droite

f'(x^{+}):=\lim _{h\to 0^{+}}{\frac {f(x+h)-f(x)}{h}}

et la limite gauche

f'(x^{-}):=\lim _{h\to 0^{-}}{\frac {f(x+h)-f(x)}{h}}

existent dans la droite réelle étendue $[-\infty, \infty]$ , alors il existe un certain nombre $c$ dans l'intervalle ouvert $(a, b)$ tel que l'une des deux limites

f'(c^{+})\quad {\text{et}}\quad f'(c^{-})

est 0 et l'autre est ≤ 0 (dans la ligne réelle étendue). Si les limites droite et gauche concordent pour tout $x$ , alors elles concordent en particulier pour $c$ , donc la dérivée de $f$ existe en $c$ et est égale à zéro.

Remarques

Si $f$ est convexe ou concave, alors les dérivées à droite et à gauche existent à chaque point intérieur, d'où les limites ci-dessus existent et sont des nombres réels.
Cette version généralisée du théorème est suffisante pour prouver la convexité lorsque les dérivées unilatérales sont monotones croissantes :

f'(x^{-})\leq f'(x^{+})\leq f'(y^{-}),\qquad x<y.

Preuve de la version généralisée

Puisque la preuve pour la version standard du théorème de Rolle et la généralisation sont très similaires, nous prouvons la généralisation.

L'idée de la preuve est de soutenir que si $f (a) = f (b)$ , alors $f$ doit atteindre un maximum ou un minimum quelque part entre $a$ et $b$ , disons en $c$ , et la fonction doit passer de croissante à décroissante ( ou l'inverse) à $c$ . En particulier, si la dérivée existe, elle doit être nulle en $c$ .

Par hypothèse, $f$ est continue sur $[a, b]$ , et par le théorème des valeurs extrêmes atteint à la fois son maximum et son minimum dans $[a, b]$ . Si ceux-ci sont tous deux atteints aux extrémités de $[a, b]$ , alors $f$ est constant sur $[a, b]$ et donc la dérivée de $f$ est nulle en chaque point de $(a, b)$ .

Supposons alors que le maximum soit obtenu en un point intérieur $c$ de $(a, b)$ (l'argument pour le minimum est très similaire, considérons simplement $- f$ ). Nous examinerons séparément les limites droite et gauche ci-dessus.

Pour un réel $h$ tel que $c + h$ est dans $[a, b]$ , la valeur $f (c + h)$ est inférieure ou égale à $f (c)$ car $f$ atteint son maximum en $c$ . Par conséquent, pour tout $h > 0$ ,

{\frac {f(c+h)-f(c)}{h}}\leq 0,

Par conséquent

f'(c^{+}):=\lim _{h\to 0^{+}}{\frac {f(c+h)-f(c)}{h}}\leq 0 ,

là où la limite existe par hypothèse, elle peut être moins l'infini.

De même, pour chaque $h < 0$ , l'inégalité se retourne car le dénominateur est maintenant négatif et nous obtenons

{\frac {f(c+h)-f(c)}{h}}\geq 0,

Par conséquent

f'(c^{-}):=\lim _{h\to 0^{-}}{\frac {f(c+h)-f(c)}{h}}\geq 0 ,

où la limite pourrait être plus l'infini.

Enfin, lorsque les limites droite et gauche ci-dessus concordent (en particulier lorsque $f$ est dérivable), alors la dérivée de $f$ en $c$ doit être nulle.

(Alternativement, nous pouvons appliquer directement le théorème du point stationnaire de Fermat .)

Généralisation aux dérivés supérieurs

On peut aussi généraliser le théorème de Rolle en exigeant que $f$ ait plus de points avec des valeurs égales et une plus grande régularité. Concrètement, supposons que

la fonction $f$ est $n - 1$ fois continûment dérivable sur l'intervalle fermé $[a, b]$ et la dérivée $n$ existe sur l' intervalle ouvert $(a, b)$ , et
il existe $n$ intervalles donnés par $a 1 < b 1 \leq a 2 < b 2 \leq \dots \leq a n < b n$ dans $[a, b]$ tels que $f (a k) = f (b k)$ pour tout $k$ de 1 à $n$ .

Alors il existe un nombre $c$ dans $(a, b)$ tel que la dérivée $n$ de $f$ en $c$ est nulle.

La courbe rouge est le graphe de fonction à 3 racines dans l'intervalle

[-3, 2]

. Ainsi, sa dérivée seconde (représentée en vert) a également une racine dans le même intervalle.

Les exigences concernant la dérivée $n$ de $f$ peuvent être affaiblies comme dans la généralisation ci-dessus, donnant les assertions correspondantes (éventuellement plus faibles) pour les limites droite et gauche définies ci-dessus avec $f (n - 1)$ à la place de $f$ .

En particulier, cette version du théorème affirme que si une fonction suffisamment dérivable a $n$ racines (donc elles ont la même valeur, c'est-à-dire 0), alors il existe un point interne où $f (n - 1)$ s'annule.

Preuve

La preuve utilise l'induction mathématique . Le cas $n = 1$ est simplement la version standard du théorème de Rolle. Pour $n > 1$ , prendre comme hypothèse d'induction que la généralisation est vraie pour $n - 1$ . Nous voulons le prouver pour $n$ . Supposons que la fonction $f$ satisfait les hypothèses du théorème. Par la version standard du théorème de Rolle, pour tout entier $k$ de 1 à $n$ , il existe un $c k$ dans l'intervalle ouvert $(a k, b k)$ tel que $f (c k) = 0$ . Par conséquent, la dérivée première satisfait les hypothèses sur les $n - 1$ intervalles fermés $[c 1, c 2], \dots, [c n - 1, c n]$ . Par hypothèse de récurrence, il y a un $c$ de telle sorte que la $(n - 1)$ dérivé de st $f'$ à $c$ est égal à zéro.

Généralisations à d'autres domaines

Le théorème de Rolle est une propriété des fonctions dérivables sur les nombres réels, qui sont un corps ordonné . En tant que tel, il ne se généralise pas à d'autres domaines , mais le corollaire suivant le fait : si un polynôme réel se factorise (a toutes ses racines) sur les nombres réels, alors sa dérivée le fait aussi. On peut appeler cette propriété d'un champ propriété de Rolle . Les champs plus généraux n'ont pas toujours des fonctions différentiables, mais ils ont toujours des polynômes, qui peuvent être symboliquement différenciés. De même, des champs plus généraux peuvent ne pas avoir d'ordre, mais on a une notion de racine d'un polynôme se trouvant dans un champ.

Ainsi le théorème de Rolle montre que les nombres réels ont la propriété de Rolle. Tout champ algébriquement clos tel que les nombres complexes a la propriété de Rolle. Cependant, les nombres rationnels ne sont pas – par exemple, $x 3 - x = x (x - 1)(x + 1)$ facteurs sur les rationnels , mais sa dérivée,

3x^{2}-1=3\left(x-{\tfrac {1}{\sqrt {3}}}\right)\left(x+{\tfrac {1}{\sqrt {3} }}\droite),

ne fait pas. La question de savoir quels champs satisfont à la propriété de Rolle a été soulevée dans ( Kaplansky 1972 ). Pour les corps finis , la réponse est que seuls $F 2$ et $F 4$ ont la propriété de Rolle.

Pour une version complexe, voir l' index de Voorhoeve .

Voir également

Les références

Lectures complémentaires

Leithold, Louis (1972). Le calcul, avec la géométrie analytique (2e éd.). New York : Harper & Row. p. 201-207. ISBN 0-06-043959-9.
Taylor, Angus E. (1955). Calcul avancé . Boston : Ginn et Compagnie. p. 30-37.

Liens externes

"Théorème de Rolle" , Encyclopédie des mathématiques , EMS Press , 2001 [1994]
Théorèmes de Rolle et de la valeur moyenne à couper le nœud .
Preuve du système Mizar : http://mizar.org/version/current/html/rolle.html#T2

Languages

In other projects