Ajout de Minkowski - Minkowski addition

Le chiffre rouge est la somme de Minkowski des chiffres bleus et verts.

En géométrie , la somme de Minkowski (également connue sous le nom de dilatation ) de deux ensembles de vecteurs de position A et B dans l' espace euclidien est formée en ajoutant chaque vecteur de A à chaque vecteur de B , c'est-à-dire l'ensemble

${\displaystyle A+B=\{\mathbf {a} +\mathbf {b} \,|\,\mathbf {a} \in A,\ \mathbf {b} \in B\}.}$

De manière analogue, la différence de Minkowski (ou différence géométrique) est définie en utilisant l' opération de complément comme

${\displaystyle AB=\gauche(A^{c}+(-B)\droit)^{c}}$

En général . Par exemple, dans un cas unidimensionnel et la différence de Minkowski , alors que${\style d'affichage AB\neq A+(-B)}$${\style d'affichage A=[-2,2]}$${\style d'affichage B=[-1,1]}$${\displaystyle AB=[-1,1]}$${\style d'affichage A+(-B)=A+B=[-3,3].}$

Dans un cas bidimensionnel, la différence de Minkowski est étroitement liée à l' érosion (morphologie) dans le traitement d'images .

Le concept porte le nom d' Hermann Minkowski .

Exemple

Ajout d'ensembles de Minkowski . La somme des carrés et est le carré${\displaystyle Q_{1}=[0,1]^{2}}$${\displaystyle Q_{2}=[1,2]^{2}}$${\displaystyle Q_{1}+Q_{2}=[1,3]^{2}.}$

Somme de Minkowski A + B

B

UNE

Par exemple, si nous avons deux ensembles A et B , chacun constitué de trois vecteurs de position (informellement, trois points), représentant les sommets de deux triangles dans , avec des coordonnées ${\displaystyle \mathbb {R} ^{2}}$

${\style d'affichage A=\{(1,0),(0,1),(0,-1)\}}$

et

${\displaystyle B=\{(0,0),(1,1),(1,-1)\}}$

alors leur somme de Minkowski est

${\style d'affichage A+B=\{(1,0),(2,1),(2,-1),(0,1),(1,2),(1,0),(0,- 1),(1,0),(1,-2)\}}$

qui comprend les sommets d'un hexagone.

Pour l'addition de Minkowski, l' ensemble zéro , contenant uniquement le vecteur zéro , 0, est un élément d'identité : pour tout sous-ensemble S d'un espace vectoriel, ${\style d'affichage \{0\},}$

${\style d'affichage S+\{0\}=S.}$

L' ensemble vide est important dans l'addition de Minkowski, car l'ensemble vide annihile tout autre sous-ensemble : pour chaque sous-ensemble S d'un espace vectoriel, sa somme avec l'ensemble vide est vide :

${\displaystyle S+\emptyset =\emptyset .}$

Pour un autre exemple, tenez compte des sommes Minkowski de boules ouvertes ou fermées dans le domaine qui est soit les nombres réels ou des nombres complexes Si est la boule fermée de rayon centrée sur en alors pour tout et aussi tiendra pour tout scalaire tel que le produit est défini (ce qui arrive quand ou ). Si et sont tous non nuls, les mêmes égalités seraient toujours valables si elles avaient été définies comme étant la boule ouverte, plutôt que la boule fermée, centrée sur (l'hypothèse non nulle est nécessaire car la boule ouverte de rayon est l'ensemble vide) . La somme de Minkowski d'une boule fermée et d'une boule ouverte est une boule ouverte. Plus généralement, la somme de Minkowski d'un sous-ensemble ouvert avec tout autre ensemble sera un sous-ensemble ouvert. ${\displaystyle \mathbb {K} ,}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} .}$${\displaystyle B_{r}:=\{s\in \mathbb {K} :|s|\leq r\}}$${\displaystyle r\in [0,\infty ]}$${\style d'affichage 0}$${\displaystyle \mathbb {K} }$${\displaystyle r,s\in [0,\infty ],}$ ${\style d'affichage B_{r}+B_{s}=B_{r+s}}$${\displaystyle cB_{r}=B_{|c|r}}$${\displaystyle c\in \mathbb {K} }$${\style d'affichage |c|r}$${\style d'affichage c\neq 0}$${\displaystyle r\neq \infty }$${\style d'affichage r,s,}$${\style d'affichage c}$${\style d'affichage B_{r}}$${\style d'affichage 0}$${\style d'affichage 0}$

Si est le graphique de et si et est l' axe - dans alors la somme de Minkowski de ces deux sous-ensembles fermés du plan est l' ensemble ouvert constitué de tout autre que l' axe -. Cela montre que la somme de Minkowski de deux ensembles fermés n'est pas nécessairement un ensemble fermé. Cependant, la somme de Minkowski de deux sous-ensembles fermés sera un sous-ensemble fermé si au moins un de ces ensembles est également un sous-ensemble compact . ${\displaystyle G=\left\{\left(x,1/x\right):0\neq x\in \mathbb {R} \right\}}$${\displaystyle f(x)={\frac {1}{x}}}$${\displaystyle Y=\{0\}\times \mathbb {R} }$${\style d'affichage y}$${\displaystyle X=\mathbb {R} ^{2}}$ ${\displaystyle G+Y=\{(x,y)\in \mathbb {R} ^{2}:x\neq 0\}=\mathbb {R} ^{2}\setminus Y}$${\style d'affichage y}$

Coques convexes de sommes de Minkowski

L'addition de Minkowski se comporte bien par rapport à l'opération de prise d' enveloppes convexes , comme le montre la proposition suivante :

Pour tous les sous-ensembles non vides et d'un espace vectoriel réel, l'enveloppe convexe de leur somme de Minkowski est la somme de Minkowski de leurs enveloppes convexes : ${\style d'affichage S_{1}}$${\style d'affichage S_{2}}$

${\displaystyle \operatorname {Conv} (S_{1}+S_{2})=\operatorname {Conv} (S_{1})+\operatorname {Conv} (S_{2}).}$

Ce résultat est plus généralement valable pour toute collection finie d'ensembles non vides :

${\displaystyle \operatorname {Conv} \left(\sum {S_{n}}\right)=\sum \operatorname {Conv} (S_{n}).}$

Dans la terminologie mathématique, les opérations de sommation de Minkowski et de formation d'enveloppes convexes sont des opérations de commutation .

Si est un ensemble convexe alors est aussi un ensemble convexe ; en outre ${\style d'affichage S}$${\displaystyle \mu S+\lambda S}$

${\displaystyle \mu S+\lambda S=(\mu +\lambda )S}$

pour chaque . Inversement, si cette « propriété distributive » est valable pour tous les nombres réels non négatifs, , alors l'ensemble est convexe. ${\displaystyle \mu ,\lambda \geq 0}$${\displaystyle \mu ,\lambda }$

Un exemple d'ensemble non convexe tel que ${\style d'affichage A+A\neq 2A.}$

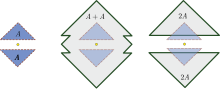
La figure de droite montre un exemple d'ensemble non convexe pour lequel ${\style d'affichage A+A\supsetneq 2A.}$

Un exemple en dimension est : Il peut être facilement calculé que mais donc encore une fois${\style d'affichage 1}$${\displaystyle B=[1,2]\cup [4,5].}$${\displaystyle 2B=[2,4]\cup [8,10]}$${\displaystyle B+B=[2,4]\cup [5,7]\cup [8,10],}$${\displaystyle B+B\supsetneq 2B.}$

Les sommes de Minkowski agissent linéairement sur le périmètre des corps convexes à deux dimensions : le périmètre de la somme est égal à la somme des périmètres. De plus, si est (l'intérieur d') une courbe de largeur constante , alors la somme de Minkowski de et de sa rotation est un disque. Ces deux faits peuvent être combinés pour donner une courte démonstration du théorème de Barbier sur le périmètre des courbes de largeur constante. ${\style d'affichage K}$${\style d'affichage K}$${\displaystyle 180^{\circ }}$

Applications

L'addition de Minkowski joue un rôle central en morphologie mathématique . Il apparaît dans le paradigme du pinceau et du trait de l'infographie 2D (avec diverses utilisations, notamment par Donald E. Knuth dans Metafont ), et comme l' opération de balayage solide de l'infographie 3D . Il a également été démontré qu'il est étroitement lié à la distance du Earth mover et, par extension, au transport optimal .

Planification de mouvement

Les sommes de Minkowski sont utilisées dans la planification du mouvement d'un objet parmi les obstacles. Ils sont utilisés pour le calcul de l' espace de configuration , qui est l'ensemble de toutes les positions admissibles de l'objet. Dans le modèle simple du mouvement de translation d'un objet dans le plan, où la position d'un objet peut être uniquement spécifiée par la position d'un point fixe de cet objet, l'espace de configuration est la somme de Minkowski de l'ensemble des obstacles et du mobile objet placé à l'origine et pivoté de 180 degrés.

Usinage à commande numérique (NC)

En usinage à commande numérique , la programmation de l'outil CN exploite le fait que la somme de Minkowski de la pièce coupante avec sa trajectoire donne la forme de la coupe dans la matière.

Modélisation solide 3D

Dans OpenSCAD, les sommes de Minkowski sont utilisées pour décrire une forme avec une autre forme créant un composite des deux formes.

Théorie de l'agrégation

Les sommes de Minkowski sont également fréquemment utilisées dans la théorie de l'agrégation lorsque les objets individuels à agréger sont caractérisés via des ensembles.

Détection de collision

Les sommes de Minkowski, en particulier les différences de Minkowski, sont souvent utilisées avec les algorithmes GJK pour calculer la détection de collision pour les coques convexes dans les moteurs physiques .

Algorithmes pour le calcul des sommes de Minkowski

Addition de Minkowski et coques convexes. Les seize points rouge foncé (à droite) forment la somme de Minkowski des quatre ensembles non convexes (à gauche), dont chacun est constitué d'une paire de points rouges. Leurs enveloppes convexes (en rose ombré) contiennent des signes plus (+) : le signe plus droit est la somme des signes plus gauche.

Cas planaire

Deux polygones convexes dans le plan

Pour deux polygones convexes P et Q dans le plan avec m et n sommets, leur somme de Minkowski est un polygone convexe avec au plus m + n sommets et peut être calculé en temps O( m + n ) par une procédure très simple, qui peut être décrit de manière informelle comme suit. Supposons que les bords d'un polygone soient donnés et la direction, disons, dans le sens inverse des aiguilles d'une montre, le long de la limite du polygone. On voit alors facilement que ces arêtes du polygone convexe sont ordonnées par angle polaire . Nous pouvons fusionner les séquences ordonnées des bords dirigés à partir de P et Q en une seule séquence ordonnée S . Imaginez que ces bords sont des flèches pleines qui peuvent être déplacées librement tout en les gardant parallèles à leur direction d'origine. Assemblez ces flèches dans l'ordre de la séquence S en attachant la queue de la flèche suivante à la tête de la flèche précédente. Il s'avère que la chaîne polygonale résultante sera en fait un polygone convexe qui est la somme de Minkowski de P et Q .

Autre

Si un polygone est convexe et un autre ne l'est pas, la complexité de leur somme de Minkowski est O(nm). Si les deux sont non convexes, leur complexité en somme de Minkowski est O((mn) ² ).

Somme Minkowski essentielle

Il existe également une notion de somme de Minkowski essentielle + _e de deux sous-ensembles de l'espace euclidien. La somme de Minkowski habituelle peut s'écrire sous la forme

${\displaystyle A+B=\left\{z\in \mathbb {R} ^{n}\,|\,A\cap (zB)\neq \emptyset \right\}.}$

Ainsi, la somme de Minkowski essentielle est définie par

${\displaystyle A+_{\mathrm {e} }B=\left\{z\in \mathbb {R} ^{n}\,|\,\mu \left[A\cap (zB)\right] >0\droit\},}$

où μ désigne la mesure de Lebesgue n- dimensionnelle . La raison du terme "essentiel" est la propriété suivante des fonctions indicatrices : tandis que

${\displaystyle 1_{A\,+\,B}(z)=\sup _{x\,\in \,\mathbb {R} ^{n}}1_{A}(x)1_{B}( zx),}$

on peut voir que

${\displaystyle 1_{A\,+_{\mathrm {e} }\,B}(z)=\mathop {\mathrm {ess\,sup} } _{x\,\in \,\mathbb {R } ^{n}}1_{A}(x)1_{B}(zx),}$

où "ess sup" désigne le supremum essentiel .

L ^p somme de Minkowski

Pour K et L sous-ensembles convexes compacts dans , la somme de Minkowski peut être décrite par la fonction de support des ensembles convexes : ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle h_{K+L}=h_{K}+h_{L}.}$

Pour p 1 , Firey a défini la somme de L ^p Minkowski K + _p L des ensembles convexes compacts K et L en contenant l'origine comme ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle h_{K+_{p}L}^{p}=h_{K}^{p}+h_{L}^{p}.}$

Par l' inégalité de Minkowski , la fonction h _{K+ p L} est encore positive homogène et convexe et donc la fonction de support d'un ensemble compact convexe. Cette définition est fondamentale dans la théorie L ^p Brunn-Minkowski.

Voir également

• somme de Blaschke
• Théorème de Brunn-Minkowski , une inégalité sur les volumes des sommes de Minkowksi
• Convolution
• Dilatation
• Érosion
• Arithmétique d'intervalle
• Volume mixte (alias Quermassintegral ou volume intrinsèque )
• Courbe parallèle
• Lemme de Shapley–Folkman
• Ensemble
• Espace vectoriel topologique#Propriétés
• Zonotope

Remarques

Les références

• Flèche, Kenneth J. ; Hahn, Frank H. (1980). Analyse concurrentielle générale . Manuels avancés en économie. 12 (réimpression de (1971) San Francisco, CA : Holden-Day, Inc. Textes d'économie mathématique.  6  éd.). Amsterdam : Hollande du Nord. ISBN 978-0-444-85497-1. MR  0439057 .
• Gardner, Richard J. (2002), « L'inégalité de Brunn-Minkowski », Bull. Amer. Math. Soc. (NS) , 39 (3) : 355–405 (électronique), doi : 10.1090/S0273-0979-02-00941-2
• Vert, Jerry ; Heller, Walter P. (1981). "1 Analyse mathématique et convexité avec applications à l'économie". Dans Flèche, Kenneth Joseph ; Intriligateur, Michael D (éd.). Manuel d'économie mathématique, tome  I. Manuels d'économie. 1 . Amsterdam : North-Holland Publishing Co. pp. 15-52. doi : 10.1016/S1573-4382(81)01005-9 . ISBN 978-0-444-86126-9. MR  0634800 .
• Henry Mann (1976), Addition Theorems: The Addition Theorems of Group Theory and Number Theory (Réimpression corrigée de 1965 Wiley ed.), Huntington, New York: Robert E. Krieger Publishing Company, ISBN 978-0-88275-418-5– via http://www.krieger-publishing.com/subcats/MathematicsandStatistics/mathematicsandstatistics.html
• Rockafellar, R. Tyrrell (1997). Analyse convexe . Repères de Princeton en mathématiques (Réimpression de la série mathématique de Princeton de 1979,  28  éd.). Princeton, New Jersey : Princeton University Press. p. xviii+451. ISBN 978-0-691-01586-6. MR  1451876 .
• Nathanson, Melvyn B. (1996), Additive Number Theory: Inverse Problems and Geometry of Sumsets , GTM, 165 , Springer, Zbl  0859.11003.
• D'accord, Edouard ; Sharir, Micha (2006), "Minkowski Sums of Monotone and General Simple Polygons", Discrete and Computational Geometry , 35 (2) : 223-240, doi : 10.1007/s00454-005-1206-y.
• Schneider, Rolf (1993), Corps convexes : la théorie de Brunn-Minkowski , Cambridge : Cambridge University Press.
• Tao, Terence & Vu, Van (2006), Additive Combinatorics , Cambridge University Press.
• Mayer, A.; Zelenyuk, V. (2014). "Agrégation des indices de productivité de Malmquist permettant la réaffectation des ressources" . Journal Européen de Recherche Opérationnelle . 238 (3) : 774-785. doi : 10.1016/j.ejor.2014.04.003 .
• Zelenyuk, V (2015). "Agrégation de l'efficacité d'échelle" . Journal Européen de Recherche Opérationnelle . 240 (1) : 269-277. doi : 10.1016/j.ejor.2014.06.038 .

Liens externes

• « addition de Minkowski » , Encyclopédie des mathématiques , EMS Press , 2001 [1994]
• Howe, Roger (1979), On the trend to convexity of the vector sum of sets , Cowles Foundation discussion papers, 538 , Cowles Foundation for Research in Economics , Yale University
• Sommes de Minkowski , dans la bibliothèque d'algorithmes de géométrie computationnelle
• La somme de Minkowski de deux triangles et la somme de Minkowski d'un disque et d'un polygone par George Beck, The Wolfram Demonstrations Project .
• L'addition de Minkowski de formes convexes par Alexander Bogomolny : une applet
• Wikibooks : Manuel de l'utilisateur OpenSCAD/Transformations#minkowski par Marius Kintel : Application
• Application de Minkowski Addition à la robotique par Joan Gerard