Treillis carré - Square lattice
|
|
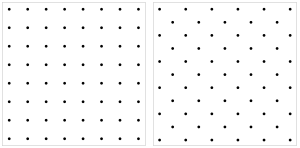
| Carré droit Simple |
carré diagonal Centré |
|---|---|

En mathématiques , le réseau carré est un type de réseau dans un espace euclidien à deux dimensions . C'est la version bidimensionnelle du réseau entier , notée Z 2 . C'est l'un des cinq types de réseaux bidimensionnels classés selon leurs groupes de symétrie ; son groupe de symétrie en notation IUC comme p4m , notation Coxeter comme [4,4] et notation orbifold comme * 442.
Deux orientations d'une image du réseau sont de loin les plus courantes. On peut les appeler commodément le réseau carré vertical et le réseau carré diagonal; ce dernier est également appelé le réseau carré centré . Ils diffèrent d'un angle de 45 °. Ceci est lié au fait qu'un réseau carré peut être divisé en deux sous-réseaux carrés, comme le montre la coloration d'un damier .
Symétrie
La catégorie de symétrie du treillis carré est le groupe de papiers peints p4m. Un motif avec ce réseau de symétrie de translation ne peut pas avoir plus, mais peut avoir moins de symétrie que le réseau lui-même. Un réseau carré vertical peut être considéré comme un réseau carré diagonal avec une taille de maillage √2 fois plus grande, avec les centres des carrés ajoutés. De manière correspondante, après avoir ajouté les centres des carrés d'un réseau carré vertical, nous avons un réseau carré diagonal avec une taille de maillage √2 fois plus petite que celle du réseau d'origine. Un motif avec une symétrie de rotation 4 fois a un réseau carré de rotocentres 4 fois qui est un facteur √2 plus fin et orienté en diagonale par rapport au réseau de symétrie de translation .
En ce qui concerne les axes de réflexion, il existe trois possibilités:
- Aucun. Ceci est le groupe de papiers peints p4.
- Dans quatre directions. C'est le groupe de papiers peints p4m.
- Dans deux directions perpendiculaires. Ceci est le groupe de papiers peints p4g. Les points d'intersection des axes de réflexion forment une grille carrée aussi fine et orientée de la même manière que le réseau carré des rotocentres quadruple, avec ces rotocentres au centre des carrés formés par les axes de réflexion.
| p4, [4,4] + , (442) | p4g, [4,4 + ], (4 * 2) | p4m, [4,4], (* 442) |
|---|---|---|
|
|
|
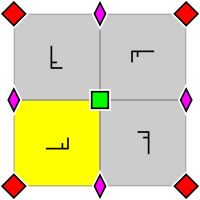
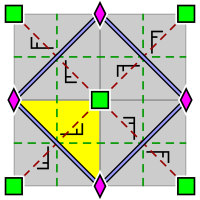
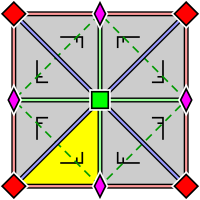
| Groupe de papier peint p4, avec la disposition dans une cellule primitive des rotocentres 2 et 4 fois (également applicable pour p4g et p4m). Un domaine fondamental est indiqué en jaune. | Groupe de papiers peints p4g. Il y a des axes de réflexion dans deux directions, pas à travers les rotocentres quadruple. | Groupe de papiers peints p4m. Il y a des axes de réflexion dans quatre directions, à travers les rotocentres quadruple. Dans deux directions, les axes de réflexion sont orientés de la même manière et aussi denses que ceux de p4g, mais décalés. Dans les deux autres directions, ils sont linéairement d'un facteur √2 plus dense. |
