Géométrie du taxi - Taxicab geometry

Géométrie du taxi par rapport à la distance euclidienne : Dans la géométrie du taxi, les chemins rouge, jaune et bleu ont tous la même longueur de chemin le plus court de 12. Dans la géométrie euclidienne, la ligne verte a une longueur et est le chemin le plus court unique.${\displaystyle 6{\sqrt {2}}\environ 8.49}$

Une géométrie de taxi est une forme de géométrie dans laquelle la fonction de distance ou métrique habituelle de la géométrie euclidienne est remplacée par une nouvelle métrique dans laquelle la distance entre deux points est la somme des différences absolues de leurs coordonnées cartésiennes . La métrique de taxi est également connu comme la distance rectiligne , L ₁ la distance , L ¹ la distance ou la norme (voir L ^p espace ), serpent la distance , la distance de bloc de ville , la distance Manhattan ou longueur Manhattan , avec des variations correspondant au nom de la géométrie. Ces derniers noms font allusion à la disposition en grille de la plupart des rues de l'île de Manhattan , ce qui fait que le chemin le plus court qu'une voiture pourrait emprunter entre deux intersections de l' arrondissement a une longueur égale à la distance des intersections dans la géométrie des taxis. ${\displaystyle \ell _{1}}$

La géométrie est utilisée dans l'analyse de régression depuis le XVIIIe siècle et est aujourd'hui souvent appelée LASSO . L'interprétation géométrique date de la géométrie non euclidienne du XIXe siècle et est due à Hermann Minkowski .

Définition formelle

La distance de taxi, , entre deux vecteurs dans un espace vectoriel réel à n dimensions avec un système de coordonnées cartésien fixe , est la somme des longueurs des projections du segment de ligne entre les points sur les axes de coordonnées . Plus formellement, ${\style d'affichage d_{1}}$${\displaystyle \mathbf {p} ,\mathbf {q} }$

${\displaystyle d_{1}(\mathbf {p} ,\mathbf {q} )=\|\mathbf {p} -\mathbf {q} \|_{1}=\sum _{i=1}^ {n}|p_{i}-q_{i}|,}$

où sont les vecteurs${\displaystyle (\mathbf {p} ,\mathbf {q} )}$

${\displaystyle \mathbf {p} =(p_{1},p_{2},\dots ,p_{n}){\text{ et }}\mathbf {q} =(q_{1},q_{2 },\points ,q_{n})\,}$

Par exemple, dans l' avion , la distance en taxi entre et est${\style d'affichage (p_{1},p_{2})}$${\style d'affichage (q_{1},q_{2})}$${\displaystyle |p_{1}-q_{1}|+|p_{2}-q_{2}|.}$

Propriétés

La distance de taxi dépend de la rotation du système de coordonnées, mais ne dépend pas de sa réflexion autour d'un axe de coordonnées ou de sa translation . La géométrie des taxis satisfait tous les axiomes de Hilbert (une formalisation de la géométrie euclidienne ) à l'exception de l' axiome côté angle-côté , car deux triangles avec deux côtés également "longs" et un angle identique entre eux ne sont généralement pas congrus à moins que les côtés mentionnés ne se produisent être parallèle.

Cercles

Cercles en géométrie de taxi discrète et continue

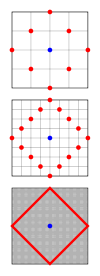
Un cercle est un ensemble de points à une distance fixe, appelée rayon , à partir d'un point appelé centre . Dans la géométrie des taxis, la distance est déterminée par une métrique différente de celle de la géométrie euclidienne, et la forme des cercles change également. Les cercles de taxi sont des carrés dont les côtés sont orientés à un angle de 45° par rapport aux axes de coordonnées. L'image de droite montre pourquoi cela est vrai, en montrant en rouge l'ensemble de tous les points avec une distance fixe d'un centre, montré en bleu. Au fur et à mesure que la taille des pâtés de maisons diminue, les points deviennent plus nombreux et deviennent un carré tourné dans une géométrie de taxi continue. Alors que chaque côté aurait une longueur en utilisant une métrique euclidienne , où r est le rayon du cercle, sa longueur dans la géométrie du taxi est de 2 r . Ainsi, la circonférence d'un cercle est de 8 r . Ainsi, la valeur d'un analogue géométrique à est de 4 dans cette géométrie. La formule du cercle unité dans la géométrie des taxis est en coordonnées cartésiennes et ${\displaystyle {\sqrt {2}}r}$${\style d'affichage \pi }$${\style d'affichage |x|+|y|=1}$

${\displaystyle r={\frac {1}{|\sin \theta |+|\cos \theta |}}}$

en coordonnées polaires .

Un cercle de rayon 1 (utilisant cette distance) est le voisinage de von Neumann de son centre.

Un cercle de rayon r de la distance de Chebyshev ( L _∞ métrique ) sur un plan est un carré avec des côtés de longueur 2 r parallèlement aux axes de coordonnées, de manière plane la distance Chebyshev peut être considéré comme équivalent par rotation et mise à l' échelle de la distance plane de taxi. Cependant, cette équivalence entre les métriques L ₁ et L _∞ ne se généralise pas aux dimensions supérieures.

Chaque fois que chaque paire dans une collection de ces cercles a une intersection non vide, il existe un point d'intersection pour toute la collection ; par conséquent, la distance de Manhattan forme un espace métrique injectif .

Applications

Mesures de distances aux échecs

Aux échecs , la distance entre les cases de l' échiquier pour les tours est mesurée en distance de taxi ; les rois et les reines utilisent la distance Chebyshev , et les évêques utilisent la distance taxi (entre les cases de la même couleur) sur l'échiquier tourné de 45 degrés, c'est-à-dire avec ses diagonales comme axes de coordonnées. Pour passer d'une case à l'autre, seuls les rois ont besoin d'un nombre de déplacements égal à leur distance respective ; les tours, les dames et les fous nécessitent un ou deux coups (sur un plateau vide, et en supposant que le coup soit possible dans le cas du fou).

Détection compressée

Lors de la résolution d'un système sous-déterminé d'équations linéaires, le terme de régularisation pour le vecteur de paramètre est exprimé en termes de -norme (géométrie de taxi) du vecteur. Cette approche apparaît dans le cadre de récupération de signal appelé détection compressée . ${\displaystyle \ell _{1}}$

Différences de distributions de fréquences

La géométrie des taxis peut être utilisée pour évaluer les différences dans les distributions de fréquences discrètes. Par exemple, dans l'épissage de l'ARN , les distributions positionnelles des hexamères , qui tracent la probabilité que chaque hexamère apparaisse à chaque nucléotide donné à proximité d'un site d'épissage, peuvent être comparées à la distance L1. Chaque distribution de position peut être représentée comme un vecteur où chaque entrée représente la probabilité que l'hexamère commence à un certain nucléotide. Une grande distance L1 entre les deux vecteurs indique une différence significative dans la nature des distributions tandis qu'une petite distance dénote des distributions de forme similaire. Cela équivaut à mesurer l'aire entre les deux courbes de distribution car l'aire de chaque segment est la différence absolue entre les vraisemblances des deux courbes à ce point. Lorsqu'il est additionné pour tous les segments, il fournit la même mesure que la distance L1.

Histoire

La métrique L ^{1 a} été utilisée dans l'analyse de régression en 1757 par Roger Joseph Boscovich . L'interprétation géométrique date de la fin du XIXe siècle et du développement des géométries non euclidiennes , notamment par Hermann Minkowski et son inégalité de Minkowski , dont cette géométrie est un cas particulier, particulièrement utilisée dans la géométrie des nombres , ( Minkowski 1910 ). La formalisation des espaces L ^p est créditée à ( Riesz 1910 ).

Voir également

• Quinze casse-tête
• Distance de Hamming  - nombre de bits qui diffèrent entre deux chaînes
• Câblage Manhattan
• Distance de Mannheim
• Métrique  – Fonction mathématique définissant la distance
• Distance de Minkowski
• Espace vectoriel normé  – Espace vectoriel sur lequel une distance est définie
• Enveloppe convexe orthogonale  - Surensemble minimal qui coupe chaque ligne parallèle à l'axe dans un intervalle
• Marche aléatoire  – Formalisation mathématique d'un chemin constitué d'une succession d'étapes aléatoires

Remarques

Les références

• Krause, Eugène F. (1987). La géométrie des taxis . Douvres. ISBN 978-0-486-25202-5.
• Minkowski, Hermann (1910). Geometrie der Zahlen (en allemand). Leipzig et Berlin : RG Teubner. JFM  41.0239.03 . MR  0249269 . Récupéré le 6 octobre 2019 .
• Riesz, Frigyes (1910). "Untersuchungen über Systeme integrierbarer Funktionen" . Mathematische Annalen (en allemand). 69 (4) : 449-497. doi : 10.1007/BF01457637 . hdl : 10338.dmlcz/128558 . S2CID  120242933 .

Liens externes

• Weisstein, Eric W. "Taxicab Metric" . MathWorld .
• Malkevitch, Joe (1er octobre 2007). "Taxi!" . Société mathématique américaine . Récupéré le 6 octobre 2019 .