Fonctions hyperboliques inverses - Inverse hyperbolic functions

Un rayon passant par l' hyperbole unitaire au point , où est le double de l'aire entre le rayon, l'hyperbole et l' axe -${\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1}$${\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)}$${\displaystyle \scriptstyle a}$${\displaystyle \scriptstyle x}$

Les fonctions hyperboliques inverses

En mathématiques , les fonctions inverses hyperboliques sont les fonctions inverses des fonctions hyperboliques .

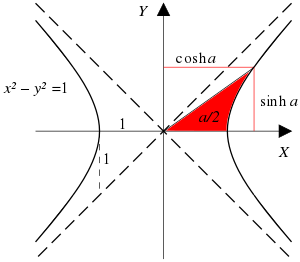
Pour une valeur donnée d'une fonction hyperbolique, la fonction hyperbolique inverse correspondante fournit l' angle hyperbolique correspondant . La taille de l'angle hyperbolique est égale à l' aire du secteur hyperbolique correspondant de l'hyperbole xy = 1 , ou deux fois l'aire du secteur correspondant de l' hyperbole unitaire x ² − y ² = 1 , tout comme un angle circulaire est deux fois l'aire du secteur circulaire du cercle unité . Certains auteurs ont appelé les fonctions hyperboliques inverses « fonctions de surface » pour réaliser les angles hyperboliques.

Les fonctions hyperboliques interviennent dans les calculs d'angles et de distances en géométrie hyperbolique . Il se produit également dans les solutions de nombreuses équations différentielles linéaires (telles que l'équation définissant une chaînette ), les équations cubiques et l'équation de Laplace en coordonnées cartésiennes . Les équations de Laplace sont importantes dans de nombreux domaines de la physique , notamment la théorie électromagnétique , le transfert de chaleur , la dynamique des fluides et la relativité restreinte .

Notation

Les abréviations les plus courantes sont celles spécifiées par la norme ISO 80000-2 . Ils consistent en ar- suivi de l'abréviation de la fonction hyperbolique correspondante (par exemple, arsinh, arcosh).

Cependant, arc- suivi de la fonction hyperbolique correspondante (par exemple, arcsinh, arccosh) est également couramment observé, par analogie avec la nomenclature des fonctions trigonométriques inverses . Ce sont des termes impropres, puisque le préfixe arc est l'abréviation de arcus , tandis que le préfixe ar représente la zone ; les fonctions hyperboliques ne sont pas directement liées aux arcs.

D'autres auteurs préfèrent utiliser la notation arg sinh, argcosh, argtanh, etc., où le préfixe arg est l'abréviation du latin argumentum . En informatique, cela est souvent abrégé en asinh .

La notation sinh ⁻¹ ( x ) , cosh ⁻¹ ( x ) , etc. la fonction inverse (par exemple, cosh ^-1 ( x ) contre cosh( x ) ^-1 ).

Définitions en termes de logarithmes

Puisque les fonctions hyperboliques sont des fonctions rationnelles de e ^x dont le numérateur et le dénominateur sont de degré au plus deux, ces fonctions peuvent être résolues en fonction de e ^x , en utilisant la formule quadratique ; puis, en prenant le logarithme népérien, on obtient les expressions suivantes pour les fonctions hyperboliques inverses.

Pour les arguments complexes , les fonctions hyperboliques inverses, la racine carrée et le logarithme sont des fonctions à valeurs multiples et les égalités des sous-sections suivantes peuvent être considérées comme des égalités de fonctions à valeurs multiples.

Pour toutes les fonctions hyperboliques inverses (sauf la cotangente hyperbolique inverse et la cosécante hyperbolique inverse), le domaine de la fonction réelle est connexe .

Sinus hyperbolique inverse

Sinus hyperbolique inverse (alias sinus hyperbolique de zone) (latin : sinus hyperbolique de zone ) :

${\displaystyle \operatorname {arsinh} x=\ln \left(x+{\sqrt {x^{2}+1}}\right)}$

Le domaine est toute la vraie ligne .

Cosinus hyperbolique inverse

Cosinus hyperbolique inverse (alias area hyperbolic cosinus ) (latin: Area cosinus hyperbolicus ):

${\displaystyle \operatorname {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right)}$

Le domaine est l' intervalle fermé [1, +∞ ) .

Tangente hyperbolique inverse

Tangente hyperbolique inverse (alias a rea tangente hyperbolique ) (latin: Area tangens hyperbolicus ):

${\displaystyle \operatorname {artanh} x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)}$

Le domaine est l' intervalle ouvert (−1, 1) .

Cotangente hyperbolique inverse

Cotangente hyperbolique inverse (alias, cotangente hyperbolique à aire ) (latin: Area cotangens hyperbolicus ):

${\displaystyle \operatorname {arcoth} x={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)}$

Le domaine est la réunion des intervalles ouverts (−∞, −1) et (1, +∞) .

Sécante hyperbolique inverse

Sécante hyperbolique inverse (alias, sécante hyperbolique à aire ) (latin : Area secans hyperbolicus ):

${\displaystyle \operatorname {arsech} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right )=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)}$

Le domaine est l'intervalle semi-ouvert (0, 1] .

Cosécante hyperbolique inverse

Cosécante hyperbolique inverse (alias, cosécante hyperbolique aire ) (latin : aire cosécanique hyperbolique ) :

${\displaystyle \operatorname {arcsch} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right )}$

Le domaine est la vraie ligne avec 0 supprimé.

Formules d'addition

${\displaystyle \operatorname {arsinh} u\pm \operatorname {arsinh} v=\operatorname {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u ^{2}}}\droit)}$

${\displaystyle \operatorname {arcosh} u\pm \operatorname {arcosh} v=\operatorname {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1 )}}\droit)}$

${\displaystyle \operatorname {artanh} u\pm \operatorname {artanh} v=\operatorname {artanh} \left({\frac {u\pm v}{1\pm uv}}\right)}$

${\displaystyle \operatorname {arcoth} u\pm \operatorname {arcoth} v=\operatorname {arcoth} \left({\frac {1\pm uv}{u\pm v}}\right)}$

${\displaystyle {\begin{aligned}\operatorname {arsinh} u+\operatorname {arcosh} v&=\operatorname {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2} -1)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\ à droite)\end{aligné}}}$

Autres identités

${\displaystyle {\begin{aligned}2\operatorname {arcosh} x&=\operatorname {arcosh} (2x^{2}-1)&\quad {\hbox{ for }}x\geq 1\\4\operatorname {arcosh} x&=\operatorname {arcosh} (8x^{4}-8x^{2}+1)&\quad {\hbox{ for }}x\geq 1\\2\operatorname {arsinh} x&=\ nom d'opérateur {arcosh} (2x^{2}+1)&\quad {\hbox{ pour }}x\geq 0\\4\nom d'opérateur {arsinh} x&=\nom d'opérateur {arcosh} (8x^{4}+8x ^{2}+1)&\quad {\hbox{ pour }}x\geq 0\end{aligned}}}$

${\displaystyle \ln(x)=\operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)=\operatorname {arsinh} \left({\frac {x ^{2}-1}{2x}}\right)=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)}$

Composition des fonctions hyperboliques et hyperboliques inverses

${\displaystyle {\begin{aligned}&\sinh(\operatorname {arcosh} x)={\sqrt {x^{2}-1}}\quad {\text{for}}\quad |x|>1 \\&\sinh(\operatorname {artanh} x)={\frac {x}{\sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x< 1\\&\cosh(\operatorname {arsinh} x)={\sqrt {1+x^{2}}}\\&\cosh(\operatorname {artanh} x)={\frac {1}{\ sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x<1\\&\tanh(\operatorname {arsinh} x)={\frac {x}{ \sqrt {1+x^{2}}}}\\&\tanh(\operatorname {arcosh} x)={\frac {\sqrt {x^{2}-1}}{x}}\quad { \text{for}}\quad |x|>1\end{aligned}}}$

Composition des fonctions hyperboliques et trigonométriques inverses

${\displaystyle \operatorname {arsinh} \left(\tan \alpha \right)=\operatorname {artanh} \left(\sin \alpha \right)=\ln \left({\frac {1+\sin \alpha }{\cos \alpha }}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\cos \alpha }}\right)}$

${\displaystyle \ln \left(\left|\tan \alpha \right|\right)=-\operatorname {artanh} \left(\cos 2\alpha \right)}$

Conversions

${\displaystyle \ln x=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)=\operatorname {arsinh} \left({ \frac {x^{2}-1}{2x}}\right)=\pm \operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)}$

${\displaystyle \operatorname {artanh} x=\operatorname {arsinh} \left({\frac {x}{\sqrt {1-x^{2}}}}\right)=\pm \operatorname {arcosh} \ gauche({\frac {1}{\sqrt {1-x^{2}}}}\droite)}$

${\displaystyle \operatorname {arsinh} x=\operatorname {artanh} \left({\frac {x}{\sqrt {1+x^{2}}}}\right)=\pm \operatorname {arcosh} \ gauche({\sqrt {1+x^{2}}}\droite)}$

${\displaystyle \operatorname {arcosh} x=\left|\operatorname {arsinh} \left({\sqrt {x^{2}-1}}\right)\right|=\left|\operatorname {artanh} \ gauche({\frac {\sqrt {x^{2}-1}}{x}}\right)\right|}$

Dérivés

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} x&{}={\frac {1}{\sqrt {x^{2}+1}}},{ \text{ pour tout réel }}x\\{\frac {d}{dx}}\operatorname {arcosh} x&{}={\frac {1}{\sqrt {x^{2}-1}}} ,{\text{ pour tout réel }}x>1\\{\frac {d}{dx}}\operatorname {artanh} x&{}={\frac {1}{1-x^{2}}} ,{\text{ pour tout réel }}|x|<1\\{\frac {d}{dx}}\operatorname {arcoth} x&{}={\frac {1}{1-x^{2} }},{\text{ pour tout réel }}|x|>1\\{\frac {d}{dx}}\operatorname {arsech} x&{}={\frac {-1}{x{\sqrt {1-x^{2}}}}},{\text{ pour tout réel }}x\in (0,1)\\{\frac {d}{dx}}\operatorname {arcsch} x&{} ={\frac {-1}{|x|{\sqrt {1+x^{2}}}}},{\text{ pour tout réel }}x{\text{, sauf }}0\\\ fin{aligné}}}$

Pour un exemple de différentiation : soit θ = arsinh x , donc (où sinh ² θ = (sinh θ ) ² ):

${\displaystyle {\frac {d\,\operatorname {arsinh} x}{dx}}={\frac {d\theta }{d\sinh \theta }}={\frac {1}{\cosh \theta }}={\frac {1}{\sqrt {1+\sinh ^{2}\theta }}}={\frac {1}{\sqrt {1+x^{2}}}}.}$

Extensions de série

Des séries d'extension peuvent être obtenues pour les fonctions ci-dessus :

${\displaystyle {\begin{aligned}\operatorname {arsinh} x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\ gauche({\frac {1\cdot 3}{2\cdot 4}}\droite){\frac {x^{5}}{5}}-\gauche({\frac {1\cdot 3\cdot 5 }{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\ gauche({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\droite){\frac {x^{2n+1}} {2n+1}},\qquad \left|x\right|<1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcosh} x&=\ln(2x)-\left(\left({\frac {1}{2}}\right){\frac {x^{-2 }}{2}}+\gauche({\frac {1\cdot 3}{2\cdot 4}}\droite){\frac {x^{-4}}{4}}+\gauche({\ frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}}+\cdots \right)\\&=\ln (2x)-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\ frac {x^{-2n}}{2n}},\qquad \left|x\right|>1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {artanh} x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}, \qquad \left|x\right|<1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcsch} x=\operatorname {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{ 2}}\right){\frac {x^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^ {-5}}{5}}-\gauche({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{ 7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n} (n!)^{2}}}\right){\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned }}}$

${\displaystyle {\begin{aligned}\operatorname {arsech} x=\operatorname {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\ gauche({\frac {1}{2}}\droite){\frac {x^{2}}{2}}+\gauche({\frac {1\cdot 3}{2\cdot 4}}\ droite){\frac {x^{4}}{4}}+\gauche({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\droite){\frac {x ^{6}}{6}}+\cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\ frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1\ fin{aligné}}}$

${\displaystyle {\begin{aligned}\operatorname {arcoth} x=\operatorname {artanh} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3} }{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n= 0}^{\infty }{\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}}$

Le développement asymptotique pour l'arsinh x est donné par

${\displaystyle \operatorname {arsinh} x=\ln(2x)+\sum \limits _{n=1}^{\infty }{\left({-1}\right)^{n-1}{\ frac {\gauche({2n-1}\droit)!!}{2n\gauche({2n}\droit)!!}}}{\frac {1}{x^{2n}}}}$

Valeurs principales dans le plan complexe

En tant que fonctions d'une variable complexe , les fonctions hyperboliques inverses sont des fonctions multivaluées qui sont analytiques , sauf en un nombre fini de points. Pour une telle fonction, il est courant de définir une valeur principale , qui est une fonction analytique à valeur unique qui coïncide avec une branche spécifique de la fonction multivaluée, sur un domaine constitué du plan complexe dans lequel un nombre fini d' arcs (généralement la moitié lignes ou segments de ligne ) ont été supprimés. Ces arcs sont appelés coupes de branches . Pour préciser la branche, c'est-à-dire définir quelle valeur de la fonction multivaluée est considérée en chaque point, on la définit généralement en un point particulier, et on en déduit la valeur partout dans le domaine de définition de la valeur principale par suite analytique . Lorsque cela est possible, il est préférable de définir directement la valeur principale, sans faire référence à la continuation analytique.

Par exemple, pour la racine carrée, la valeur principale est définie comme la racine carrée qui a une partie réelle positive . Cela définit une fonction analytique à valeur unique, qui est définie partout, sauf pour les valeurs réelles non positives des variables (où les deux racines carrées ont une partie réelle nulle). Cette valeur principale de la fonction racine carrée est notée dans ce qui suit. De même, la valeur principale du logarithme, notée dans ce qui suit, est définie comme la valeur pour laquelle la partie imaginaire a la plus petite valeur absolue. Elle est définie partout sauf pour les valeurs réelles non positives de la variable, pour lesquelles deux valeurs différentes du logarithme atteignent le minimum. ${\displaystyle {\sqrt {x}}}$${\displaystyle \operatorname {Log} }$

Pour toutes les fonctions hyperboliques inverses, la valeur principale peut être définie en termes de valeurs principales de la racine carrée et de la fonction logarithme. Cependant, dans certains cas, les formules de § Définitions en termes de logarithmes ne donnent pas une valeur principale correcte, car donnant un domaine de définition trop petit et, dans un cas non connexe .

Valeur principale du sinus hyperbolique inverse

La valeur principale du sinus hyperbolique inverse est donnée par

${\displaystyle \operatorname {arsinh} z=\operatorname {Log} (z+{\sqrt {z^{2}+1}}\,)\,.}$

L'argument de la racine carrée est un nombre réel non positif, si et seulement si z appartient à l'un des intervalles [ i , + i ∞) et (− i ∞, − i ] de l'axe imaginaire. Si l'argument de le logarithme est réel, alors il est positif. Ainsi, cette formule définit une valeur principale pour arsinh, avec des coupes de branches [ i , + i ∞) et (− i ∞, − i ] . Ceci est optimal, car les coupes de branches doivent se connecter les points singuliers i et − i à l'infini.

Valeur principale du cosinus hyperbolique inverse

La formule pour le cosinus hyperbolique inverse donnée au § Cosinus hyperbolique inverse n'est pas pratique, car similaire aux valeurs principales du logarithme et de la racine carrée, la valeur principale d'arcosh ne serait pas définie pour z imaginaire . Ainsi, la racine carrée doit être factorisée, ce qui conduit à

${\displaystyle \operatorname {arcosh} z=\operatorname {Log} (z+{\sqrt {z+1}}{\sqrt {z-1}}\,)\,.}$

Les valeurs principales des racines carrées sont toutes deux définies, sauf si z appartient à l'intervalle réel (−∞, 1] . Si l'argument du logarithme est réel, alors z est réel et a le même signe. Ainsi, la formule ci-dessus définit une valeur principale d'arcosh en dehors de l'intervalle réel (−∞, 1] , qui est donc l'unique coupe de branche.

Valeurs principales de la tangente et de la cotangente hyperboliques inverses

Les formules données au § Définitions en termes de logarithmes suggèrent

${\displaystyle {\begin{aligned}\operatorname {artanh} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {1+z}{1-z}}\right )\\\operatorname {arcoth} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {z+1}{z-1}}\right)\end{aligned} }}$

pour la définition des valeurs principales de la tangente et de la cotangente hyperboliques inverses. Dans ces formules, l'argument du logarithme est réel si et seulement si z est réel. Pour artanh, cet argument est dans l'intervalle réel (−∞, 0] , si z appartient soit à (−∞, −1] soit à [1, ∞) . Pour arcoth, l'argument du logarithme est dans (−∞ , 0] , si et seulement si z appartient à l'intervalle réel [−1, 1] .

Par conséquent, ces formules définissent des valeurs principales commodes, pour lesquelles les coupes de branches sont (−∞, −1] et [1, ∞) pour la tangente hyperbolique inverse, et [−1, 1] pour la cotangente hyperbolique inverse.

En vue d'une meilleure évaluation numérique près des coupures de branches, certains auteurs utilisent les définitions suivantes des valeurs principales, bien que la seconde introduit une singularité amovible à z = 0 . Les deux définitions de diffèrent pour les valeurs réelles de avec . Ceux de diffèrent pour les valeurs réelles de avec . ${\displaystyle \operatorname {artanh} }$${\style d'affichage z}$${\style d'affichage z>1}$${\displaystyle \operatorname {arcoth} }$${\style d'affichage z}$${\style d'affichage z\dans [0,1)}$

${\displaystyle {\begin{aligned}\operatorname {artanh} z&={\tfrac {1}{2}}\operatorname {Log} \left({1+z}\right)-{\tfrac {1}{ 2}}\operatorname {Log} \left({1-z}\right)\\\operatorname {arcoth} z&={\tfrac {1}{2}}\operatorname {Log} \left({1+{ \frac {1}{z}}}\right)-{\tfrac {1}{2}}\operatorname {Log} \left({1-{\frac {1}{z}}}\right)\ fin{aligné}}}$

Valeur principale de la cosécante hyperbolique inverse

Pour la cosécante hyperbolique inverse, la valeur principale est définie comme

${\displaystyle \operatorname {arcsch} z=\operatorname {Log} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}+1} }\,\droit)}$.

Il est défini lorsque les arguments du logarithme et de la racine carrée ne sont pas des nombres réels non positifs. La valeur principale de la racine carrée est ainsi définie en dehors de l'intervalle [− i , i ] de la droite imaginaire. Si l'argument du logarithme est réel, alors z est un nombre réel non nul, ce qui implique que l'argument du logarithme est positif.

Ainsi, la valeur principale est définie par la formule ci-dessus en dehors de la coupe de branche , constituée par l'intervalle [- i , i ] de la ligne imaginaire.

Pour z = 0 , il y a un point singulier qui est inclus dans la coupe de branche.

Valeur principale de la sécante hyperbolique inverse

Ici, comme dans le cas du cosinus hyperbolique inverse, nous devons factoriser la racine carrée. Cela donne la valeur principale

${\displaystyle \operatorname {arsech} z=\operatorname {Log} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z}}+1}}\,{ \sqrt {{\frac {1}{z}}-1}}\right).}$

Si l'argument d'une racine carrée est réel, alors z est réel, et il s'ensuit que les deux valeurs principales des racines carrées sont définies, sauf si z est réel et appartient à l'un des intervalles (−∞, 0] et [1, +∞) . Si l'argument du logarithme est réel et négatif, alors z est également réel et négatif. Il s'ensuit que la valeur principale de arsech est bien définie, par la formule ci-dessus en dehors de deux coupes de branches , les intervalles réels (−∞, 0] et [1, +∞) .

Pour z = 0 , il y a un point singulier qui est inclus dans l'une des coupes de branches.

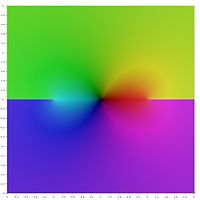
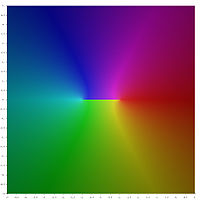
Représentation graphique

Dans la représentation graphique suivante des valeurs principales des fonctions hyperboliques inverses, les coupures de branches apparaissent comme des discontinuités de la couleur. Le fait que les coupes de branches entières apparaissent comme des discontinuités montre que ces valeurs principales ne peuvent pas être étendues à des fonctions analytiques définies sur des domaines plus larges. En d'autres termes, les coupes de branches définies ci-dessus sont minimales.

${\displaystyle \operatorname {arsinh} (z)}$

${\displaystyle \operatorname {arcosh} (z)}$

${\displaystyle \operatorname {artanh} (z)}$

${\displaystyle \operatorname {arcoth} (z)}$

${\displaystyle \operatorname {arsech} (z)}$

${\displaystyle \operatorname {arcsch} (z)}$

Fonctions hyperboliques inverses dans le plan z complexe : la couleur en chaque point du plan représente la valeur complexe de la fonction respective en ce point

Voir également

• Logarithme complexe
• Distribution sécante hyperbolique
• ISO 80000-2
• Liste des intégrales des fonctions hyperboliques inverses

Les références

Bibliographie

• Herbert Busemann et Paul J. Kelly (1953) Projective Geometry and Projective Metrics , page 207, Academic Press .

Liens externes

• "Fonctions hyperboliques inverses" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]